沪教版(上海)初中数学九年级第一学期 24.3 三角形一边上的平行线应用 课件(36张PPT)
文档属性
| 名称 | 沪教版(上海)初中数学九年级第一学期 24.3 三角形一边上的平行线应用 课件(36张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 556.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 16:46:28 | ||
图片预览




文档简介
(共36张PPT)
一类常见问题的探究
——三角形一边上的平行线应用
一类特殊的比例线段问题
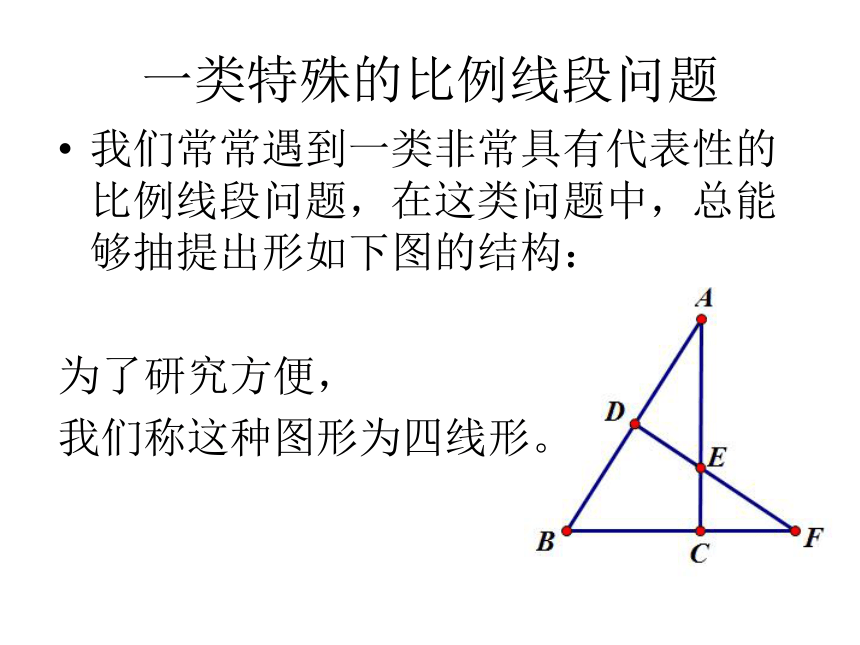
我们常常遇到一类非常具有代表性的比例线段问题,在这类问题中,总能够抽提出形如下图的结构:
为了研究方便,
我们称这种图形为四线形。
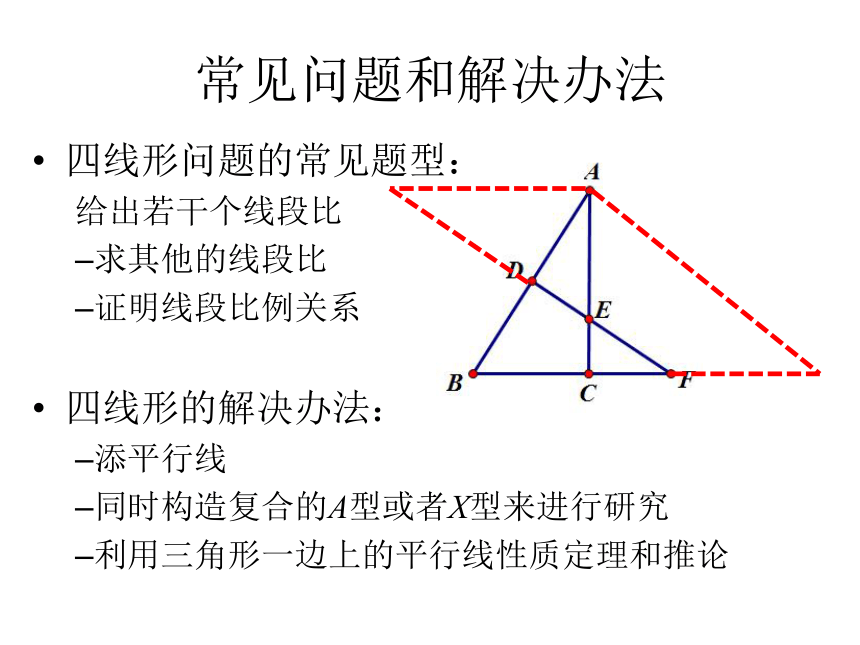
常见问题和解决办法
四线形问题的常见题型:
给出若干个线段比
求其他的线段比
证明线段比例关系
四线形的解决办法:
添平行线
同时构造复合的A型或者X型来进行研究
利用三角形一边上的平行线性质定理和推论
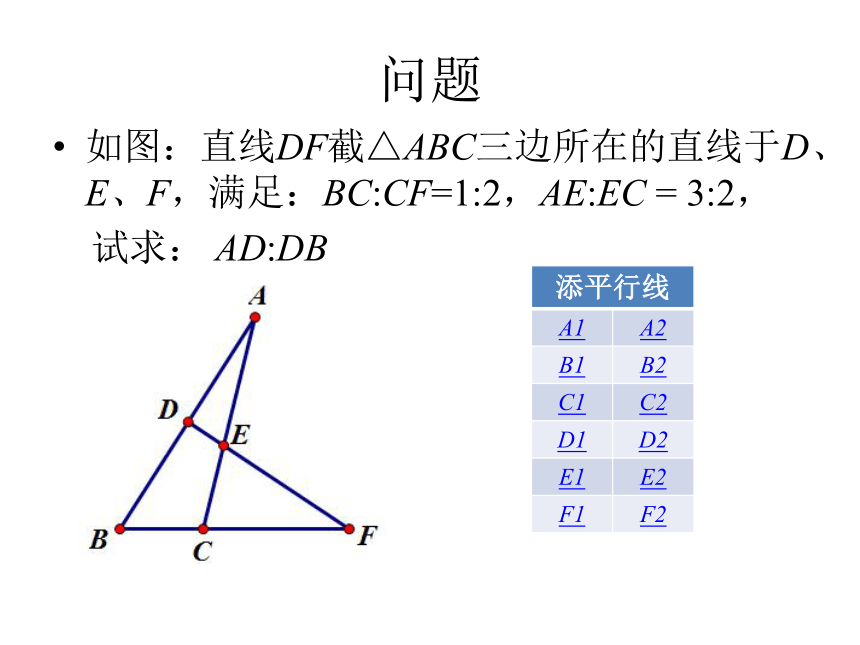
问题
如图:直线DF截△ABC三边所在的直线于D、E、F,满足:BC:CF=1:2,AE:EC
=
3:2,
试求:
AD:DB
添平行线
A1
A2
B1
B2
C1
C2
D1
D2
E1
E2
F1
F2
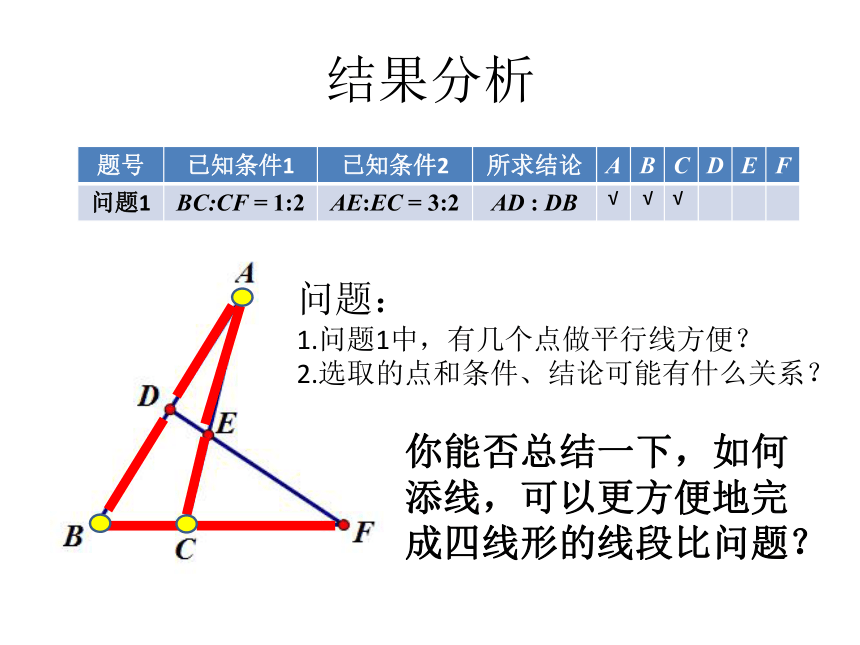
结果分析
题号
已知条件1
已知条件2
所求结论
A
B
C
D
E
F
问题1
BC:CF
=
1:2
AE:EC
=
3:2
AD
:
DB
问题:
问题1中,有几个点做平行线方便?
选取的点和条件、结论可能有什么关系?
√
√
√
你能否总结一下,如何添线,可以更方便地完成四线形的线段比问题?
总结
四线形问题的添线规律和解题步骤
首先标记已有条件和所求条件的边
经过这三条边的交点做平行线
构造复合的A型和X型的模型
借助三角形一边平行线的性质定理的推论来解决问题
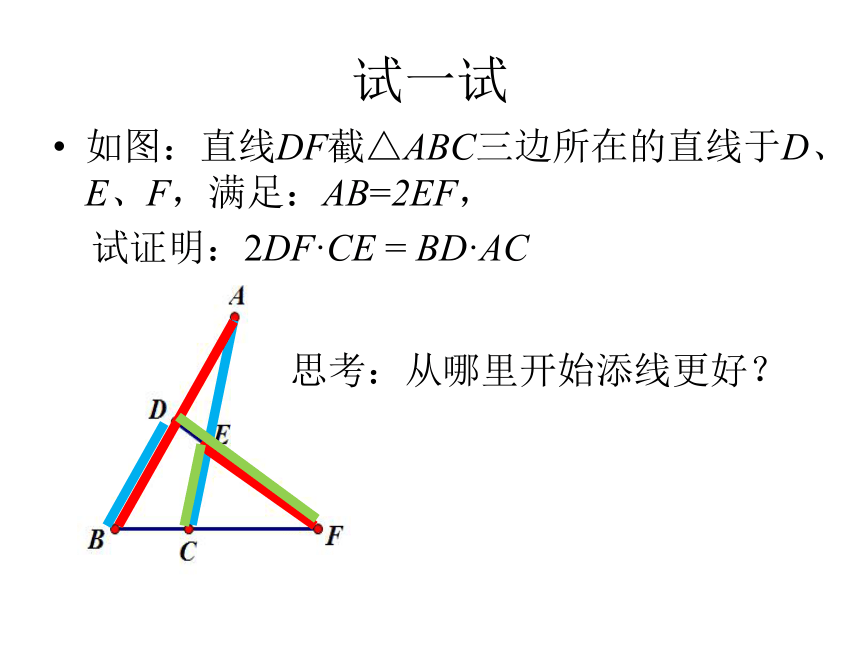
如图:直线DF截△ABC三边所在的直线于D、E、F,满足:AB=2EF,
试证明:2DF·CE
=
BD·AC
试一试
思考:从哪里开始添线更好?
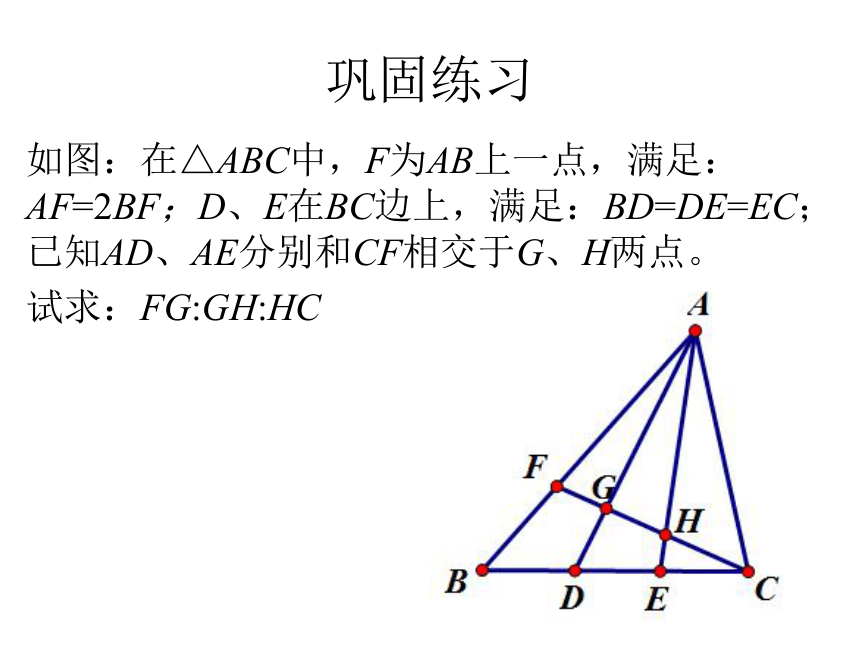
巩固练习
如图:在△ABC中,F为AB上一点,满足:AF=2BF;D、E在BC边上,满足:BD=DE=EC;已知AD、AE分别和CF相交于G、H两点。
试求:FG:GH:HC
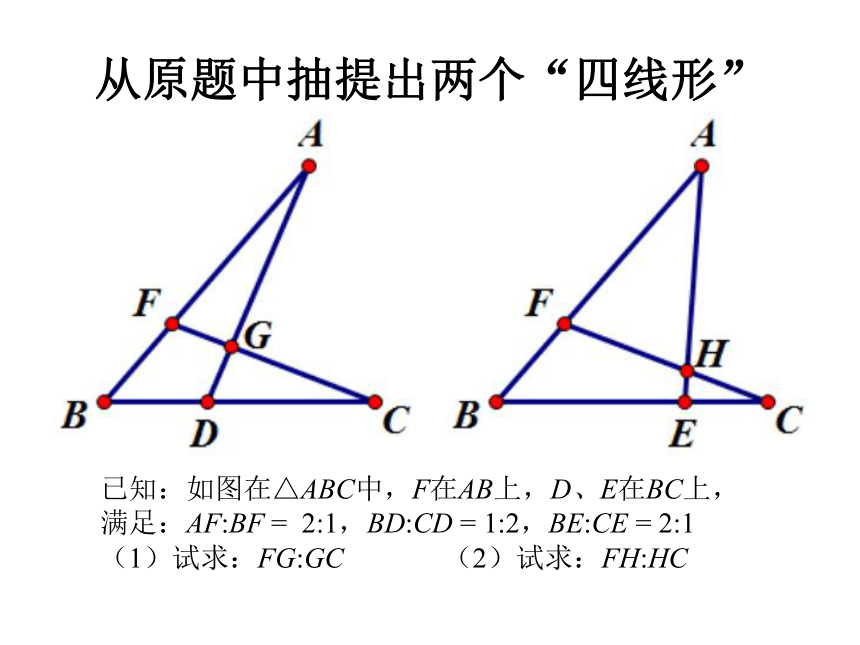
从原题中抽提出两个“四线形”
已知:如图在△ABC中,F在AB上,D、E在BC上,
满足:AF:BF
=
2:1,BD:CD
=
1:2,BE:CE
=
2:1
(1)试求:FG:GC
(2)试求:FH:HC
数学的美来自于探索
数学充满了各种规律和奥秘,
在探索的过程中,
我们不断地接近真理。
让我们借着探索来赞叹这美妙的世界!
谢谢!
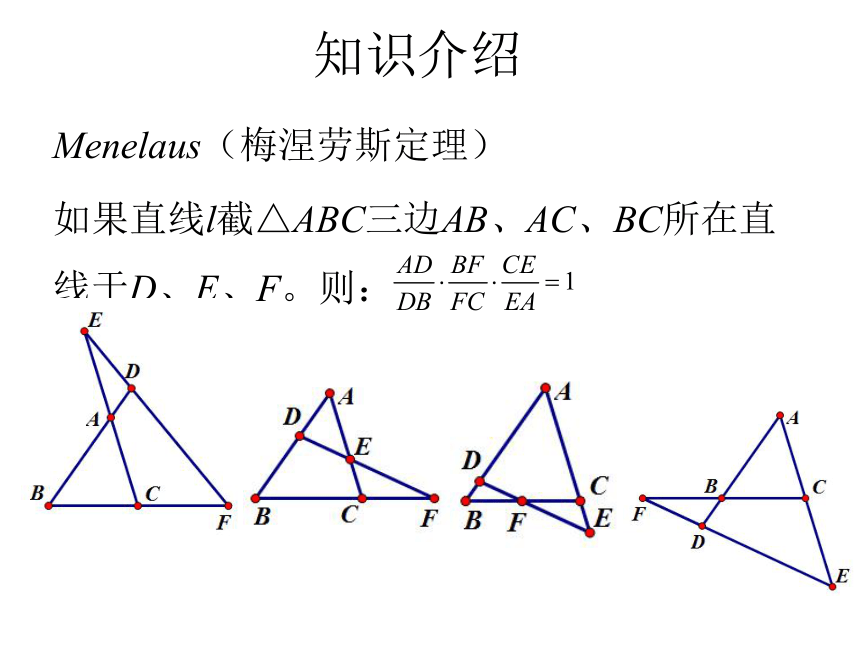
知识介绍
Menelaus(梅涅劳斯定理)
如果直线l截△ABC三边AB、AC、BC所在直线于D、E、F。则:
过A作DF的平行线,交BF延长线于P
解答
返回
过A作DF的平行线,交BF延长线于P
过A作BC的平行线,交ED延长线于P
解答
返回
过A作BC的平行线,交ED延长线于P
过B作AC的平行线,交ED延长线于P
过B作DF的平行线,交AC延长线于P
解答
返回
过B作DF的平行线,交AC延长线于P
过B作AC的平行线,交ED延长线于P
解答
返回
过C作AB的平行线,交DF于P
解答
返回
过C作AB的平行线,交DF于P
过C作DF的平行线,交AB于P
解答
返回
过C作DF的平行线,交AB于P
过D作AC的平行线,交BC于P
解答
返回
过D作AC的平行线,交BC于P
过D作BC的平行线,交AC于P
解答
返回
过D作BC的平行线,交AC于P
过E作BF的平行线,交AB于P
解答
返回
过E作BF的平行线,交AB于P
过E作BF的平行线,交BC于P
解答
返回
过E作BF的平行线,交BC于P
过F作AC的平行线,交BA延长线于P
解答
返回
过F作AC的平行线,交BA延长线于P
过F作AB的平行线,交AC延长线于P
解答
返回
过F作AB的平行线,交AC延长线于P
一类常见问题的探究
——三角形一边上的平行线应用
一类特殊的比例线段问题
我们常常遇到一类非常具有代表性的比例线段问题,在这类问题中,总能够抽提出形如下图的结构:
为了研究方便,
我们称这种图形为四线形。
常见问题和解决办法
四线形问题的常见题型:
给出若干个线段比
求其他的线段比
证明线段比例关系
四线形的解决办法:
添平行线
同时构造复合的A型或者X型来进行研究
利用三角形一边上的平行线性质定理和推论
问题
如图:直线DF截△ABC三边所在的直线于D、E、F,满足:BC:CF=1:2,AE:EC
=
3:2,
试求:
AD:DB
添平行线
A1
A2
B1
B2
C1
C2
D1
D2
E1
E2
F1
F2
结果分析
题号
已知条件1
已知条件2
所求结论
A
B
C
D
E
F
问题1
BC:CF
=
1:2
AE:EC
=
3:2
AD
:
DB
问题:
问题1中,有几个点做平行线方便?
选取的点和条件、结论可能有什么关系?
√
√
√
你能否总结一下,如何添线,可以更方便地完成四线形的线段比问题?
总结
四线形问题的添线规律和解题步骤
首先标记已有条件和所求条件的边
经过这三条边的交点做平行线
构造复合的A型和X型的模型
借助三角形一边平行线的性质定理的推论来解决问题
如图:直线DF截△ABC三边所在的直线于D、E、F,满足:AB=2EF,
试证明:2DF·CE
=
BD·AC
试一试
思考:从哪里开始添线更好?
巩固练习
如图:在△ABC中,F为AB上一点,满足:AF=2BF;D、E在BC边上,满足:BD=DE=EC;已知AD、AE分别和CF相交于G、H两点。
试求:FG:GH:HC
从原题中抽提出两个“四线形”
已知:如图在△ABC中,F在AB上,D、E在BC上,
满足:AF:BF
=
2:1,BD:CD
=
1:2,BE:CE
=
2:1
(1)试求:FG:GC
(2)试求:FH:HC
数学的美来自于探索
数学充满了各种规律和奥秘,
在探索的过程中,
我们不断地接近真理。
让我们借着探索来赞叹这美妙的世界!
谢谢!
知识介绍
Menelaus(梅涅劳斯定理)
如果直线l截△ABC三边AB、AC、BC所在直线于D、E、F。则:
过A作DF的平行线,交BF延长线于P
解答
返回
过A作DF的平行线,交BF延长线于P
过A作BC的平行线,交ED延长线于P
解答
返回
过A作BC的平行线,交ED延长线于P
过B作AC的平行线,交ED延长线于P
过B作DF的平行线,交AC延长线于P
解答
返回
过B作DF的平行线,交AC延长线于P
过B作AC的平行线,交ED延长线于P
解答
返回
过C作AB的平行线,交DF于P
解答
返回
过C作AB的平行线,交DF于P
过C作DF的平行线,交AB于P
解答
返回
过C作DF的平行线,交AB于P
过D作AC的平行线,交BC于P
解答
返回
过D作AC的平行线,交BC于P
过D作BC的平行线,交AC于P
解答
返回
过D作BC的平行线,交AC于P
过E作BF的平行线,交AB于P
解答
返回
过E作BF的平行线,交AB于P
过E作BF的平行线,交BC于P
解答
返回
过E作BF的平行线,交BC于P
过F作AC的平行线,交BA延长线于P
解答
返回
过F作AC的平行线,交BA延长线于P
过F作AB的平行线,交AC延长线于P
解答
返回
过F作AB的平行线,交AC延长线于P
