24.2 比例线段-黄金分割 课件(共22张PPT)
文档属性
| 名称 | 24.2 比例线段-黄金分割 课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:00:00 | ||
图片预览



文档简介
(共22张PPT)
如果两个多边形相似,那么这两个多边形的对应角相等,对应边的长度成比例.
一、相似形的性质
a : b = c : d,
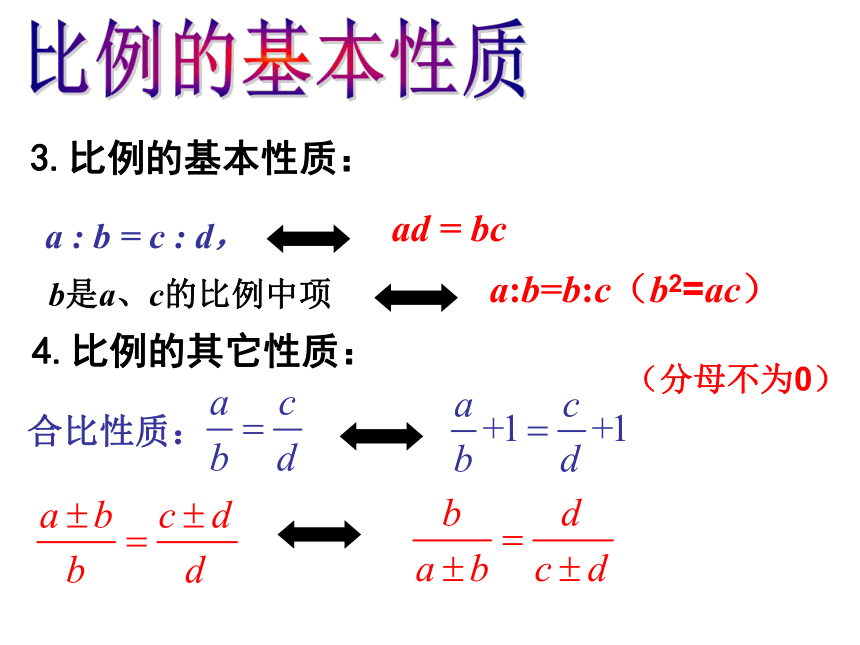
3.比例的基本性质:
ad = bc
b是a、c的比例中项
a:b=b:c(b2=ac)
4.比例的其它性质:
合比性质:
(分母不为0)
比例的等比性质:
如果 , 那么 ____________.
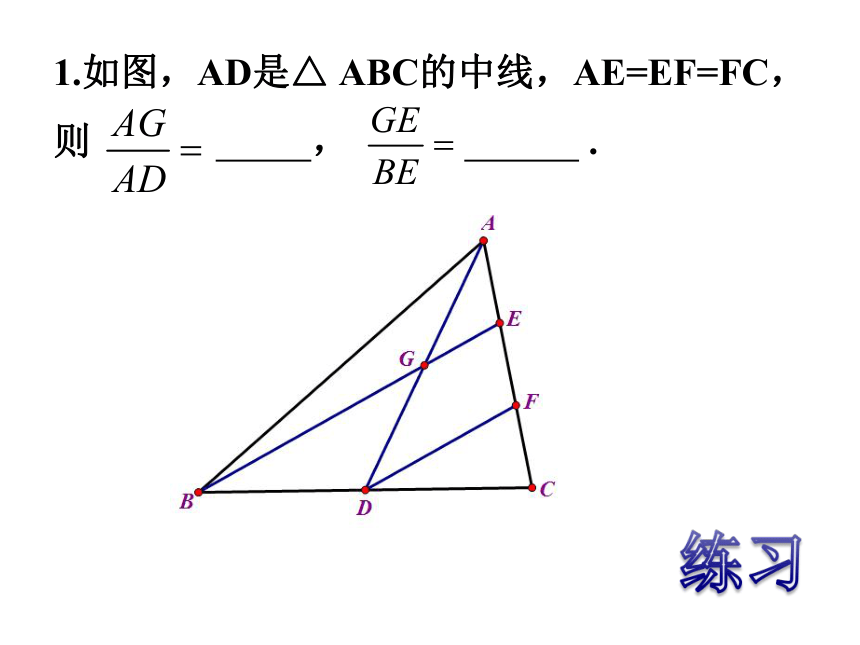
1.如图,AD是△ ABC的中线,AE=EF=FC,则 , .
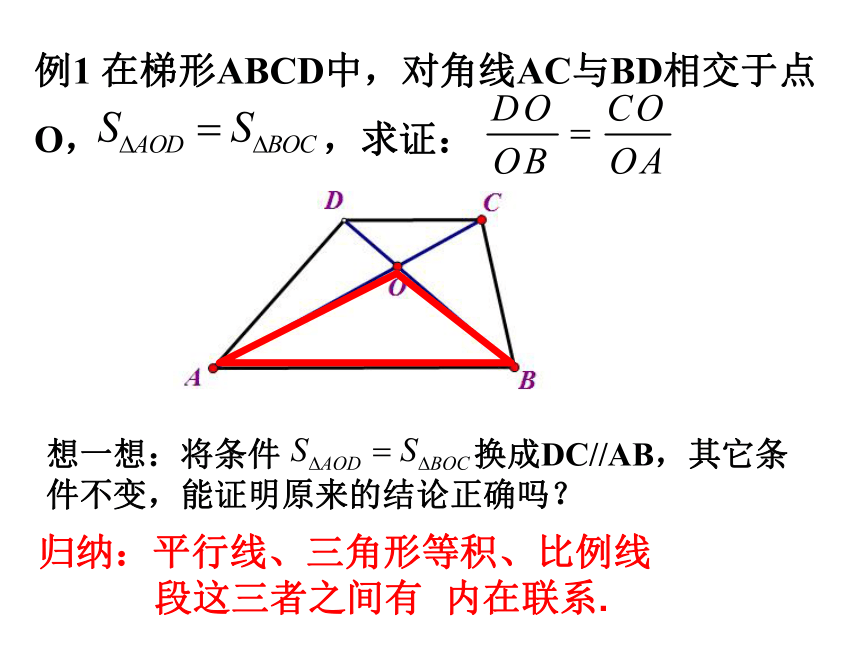
例1 在梯形ABCD中,对角线AC与BD相交于点O, ,求证:
想一想:将条件 换成DC//AB,其它条件不变,能证明原来的结论正确吗?
归纳:平行线、三角形等积、比例线
段这三者之间有 内在联系.
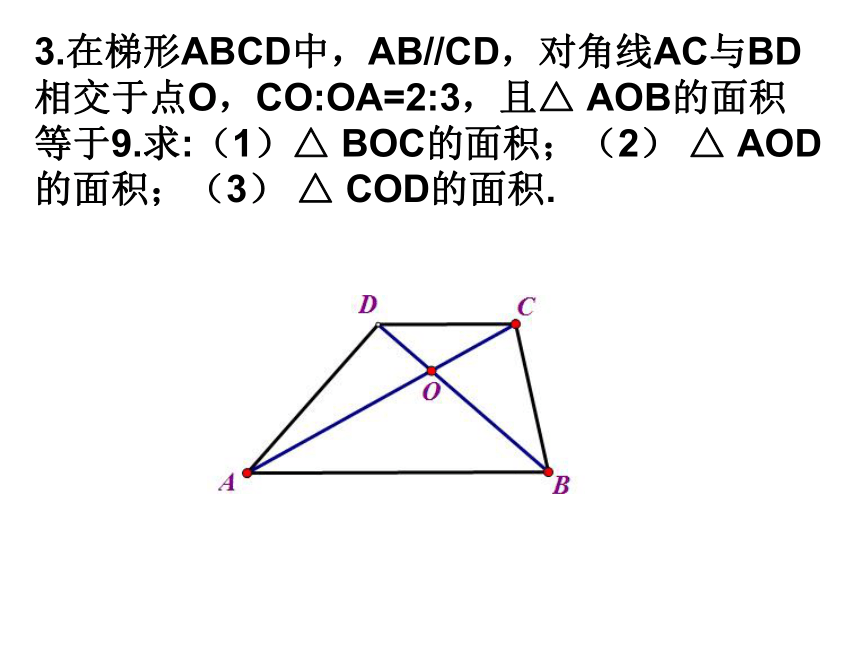
3.在梯形ABCD中,AB//CD,对角线AC与BD相交于点O,CO:OA=2:3,且△ AOB的面积等于9.求:(1)△ BOC的面积;(2) △ AOD的面积;(3) △ COD的面积.
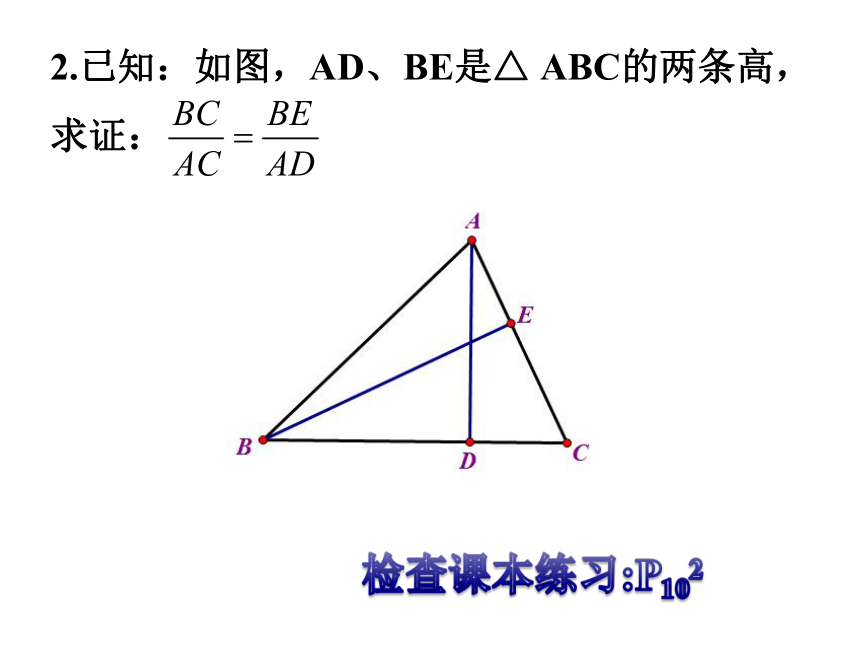
2.已知:如图,AD、BE是△ ABC的两条高,求证:
H
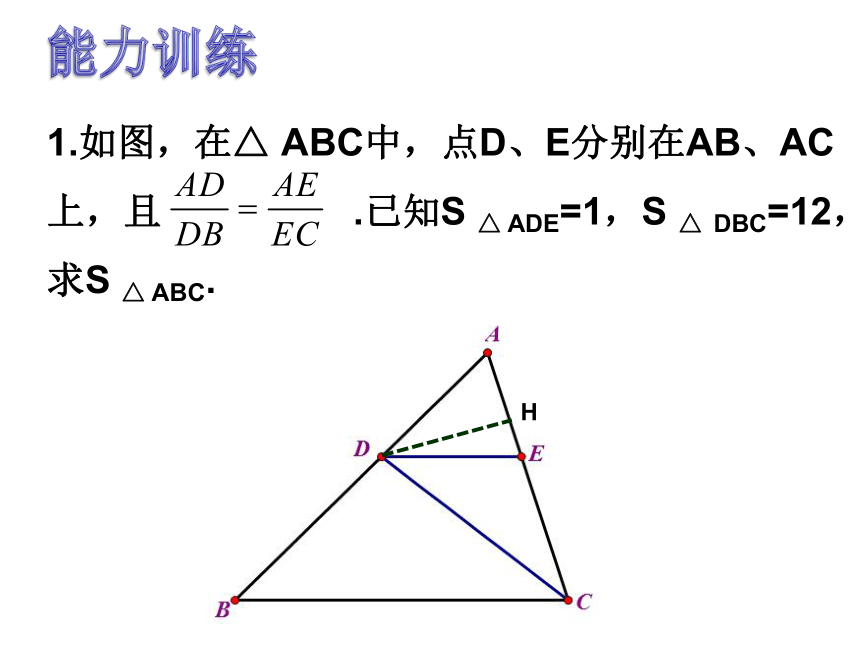
1.如图,在△ ABC中,点D、E分别在AB、AC上,且 .已知S △ ADE=1,S △ DBC=12,求S △ ABC.
3.已知四条线段长分别为1厘米, 厘米,2厘米,x厘米,它们是成比例线段,则x= 厘米.
(线段AP是PB、AB的比例中项),
例2 如图,线段AB的长度为l,点P是线段AB上一点,
求:线段AP的长.
A
P
B
P9
A
P
B
点P称为线段AB的 黄金分割点
AP与AB的比值 称为黄金分割数(简称黄金数).
它的倒数为 称为黄金分割比
A
B
P
(点P靠近B)
较长线段:AP
较短线段:BP
原线段:AB
点P称为AB的 黄金分割点
点P称为AB的 黄金分割点
黄金分割点的判断依据1
黄金分割点的判断依据2
或
想一想:一条线段的黄金分割点有 几个?
A
B
P1
∵点P1称为AB的 黄金分割点
(点P1靠近B)
(黄金数)
P2
∵点P2称为AB的 黄金分割点
(点P2靠近B)
(黄金数)
A
B
P
全
长
短
A
B
C
A
B
C
黄金矩形
D
4
1.检查课本P10练习第3题
3.如果点P是线段AB的黄金分割点,且AP>PB,则下列命题:①AB2=AP · PB,②AP2=PB · AB,③BP2=AP · AB,④AP:AB=PB:AP,其正确的是
(填序号).
4.点M是线段AB的黄金分割点,且AM>MB.则MB= ·MA.
5.如果线段AB=10厘米,点C是AB上的黄金分割点,且AC>BC,则BC的长是 厘米.
6.如果线段AB=10厘米,点C是AB上的黄金分割点,求AC的长是多少厘米?
5.以长为2厘米的定线段AB为边,作正方形ABCD,取AB的中点P,在BA的的延长线上取点F,使PF=PD.以AF为边作正方形AFEM.点M落在AD上.
(1)试求AM、DM的长;
(2)点M是线段AD的黄
金分割点吗?请说明理由.
我们做过调查,如果市场上有的电视频主要有两种,一种是宽:长为3∶4的,另一种是9∶16的.这两个比值都很接近0.618,也就是因为黄金矩形是最美的.
画家们发现,按0.618∶1来设计腿长与身高的比例,画出的人体身材最优美,
现今的女性,腰身以下的长度平均只占身高的0.58,因此古希腊维纳斯女塑像及太阳神阿波罗的形象都通过故意延长双腿,使之与身高的比值为0.618,
高与宽的比例为19比31,接近希腊人喜爱的“黄金分割比”,难怪它让人觉得优美无比
希腊--帕特农神殿
如果两个多边形相似,那么这两个多边形的对应角相等,对应边的长度成比例.
一、相似形的性质
a : b = c : d,
3.比例的基本性质:
ad = bc
b是a、c的比例中项
a:b=b:c(b2=ac)
4.比例的其它性质:
合比性质:
(分母不为0)
比例的等比性质:
如果 , 那么 ____________.
1.如图,AD是△ ABC的中线,AE=EF=FC,则 , .
例1 在梯形ABCD中,对角线AC与BD相交于点O, ,求证:
想一想:将条件 换成DC//AB,其它条件不变,能证明原来的结论正确吗?
归纳:平行线、三角形等积、比例线
段这三者之间有 内在联系.
3.在梯形ABCD中,AB//CD,对角线AC与BD相交于点O,CO:OA=2:3,且△ AOB的面积等于9.求:(1)△ BOC的面积;(2) △ AOD的面积;(3) △ COD的面积.
2.已知:如图,AD、BE是△ ABC的两条高,求证:
H
1.如图,在△ ABC中,点D、E分别在AB、AC上,且 .已知S △ ADE=1,S △ DBC=12,求S △ ABC.
3.已知四条线段长分别为1厘米, 厘米,2厘米,x厘米,它们是成比例线段,则x= 厘米.
(线段AP是PB、AB的比例中项),
例2 如图,线段AB的长度为l,点P是线段AB上一点,
求:线段AP的长.
A
P
B
P9
A
P
B
点P称为线段AB的 黄金分割点
AP与AB的比值 称为黄金分割数(简称黄金数).
它的倒数为 称为黄金分割比
A
B
P
(点P靠近B)
较长线段:AP
较短线段:BP
原线段:AB
点P称为AB的 黄金分割点
点P称为AB的 黄金分割点
黄金分割点的判断依据1
黄金分割点的判断依据2
或
想一想:一条线段的黄金分割点有 几个?
A
B
P1
∵点P1称为AB的 黄金分割点
(点P1靠近B)
(黄金数)
P2
∵点P2称为AB的 黄金分割点
(点P2靠近B)
(黄金数)
A
B
P
全
长
短
A
B
C
A
B
C
黄金矩形
D
4
1.检查课本P10练习第3题
3.如果点P是线段AB的黄金分割点,且AP>PB,则下列命题:①AB2=AP · PB,②AP2=PB · AB,③BP2=AP · AB,④AP:AB=PB:AP,其正确的是
(填序号).
4.点M是线段AB的黄金分割点,且AM>MB.则MB= ·MA.
5.如果线段AB=10厘米,点C是AB上的黄金分割点,且AC>BC,则BC的长是 厘米.
6.如果线段AB=10厘米,点C是AB上的黄金分割点,求AC的长是多少厘米?
5.以长为2厘米的定线段AB为边,作正方形ABCD,取AB的中点P,在BA的的延长线上取点F,使PF=PD.以AF为边作正方形AFEM.点M落在AD上.
(1)试求AM、DM的长;
(2)点M是线段AD的黄
金分割点吗?请说明理由.
我们做过调查,如果市场上有的电视频主要有两种,一种是宽:长为3∶4的,另一种是9∶16的.这两个比值都很接近0.618,也就是因为黄金矩形是最美的.
画家们发现,按0.618∶1来设计腿长与身高的比例,画出的人体身材最优美,
现今的女性,腰身以下的长度平均只占身高的0.58,因此古希腊维纳斯女塑像及太阳神阿波罗的形象都通过故意延长双腿,使之与身高的比值为0.618,
高与宽的比例为19比31,接近希腊人喜爱的“黄金分割比”,难怪它让人觉得优美无比
希腊--帕特农神殿
