7.2.2三角形的外角
图片预览

文档简介
7.2.2三角形的外角
教学目标
知识技能目标
三角形的外角的概念及性质;
情感体验目标
通过探索三角形的外角的性质的活动,培养学生的论证能力,拓宽他们的解题思路,从而使他们灵活应用所学的知识。
创新性目标
在体验一题多变、一题多解的过程中发散思维,提高空间想象能力。
重点与难点
教学重点:(1)了解三角形的外角的概念和性质;
(2)能利用三角形的外角的性质解决简单的实际问题。
教学难点:(1)能够证明“三角形的外角的性质;
(2)运用三角形的外角的性质解决简单的实际问题。
教法与学法
教法:按照学生的认知规律,遵循以“学生为主体,教师为主导,活动为主线”的指导思想,采用以实验观察、教师引导的教学方法。
学法:学生以自主探究为主、合作交流为辅的方法进行学习;发现学习和接受学习相结合。
教学过程
感知身边的数学
你是一个合格的检验员吗?
有一个零件的形状如图,按规定∠A=100°,∠B=20°,∠C=30°。现在量得 ∠CDB=152°,你认为这个零件合格吗?为什么?
(二)探究新知
探究活动(1)
1、请同学们在草稿纸上画一个三角形,然后把它的一边延长,得到如图所示中的∠ACD。
问题1:这个角是三角形的内角吗?
问题2:∠ACD 的特点有哪些?(从顶点和角的两边两方面思考)
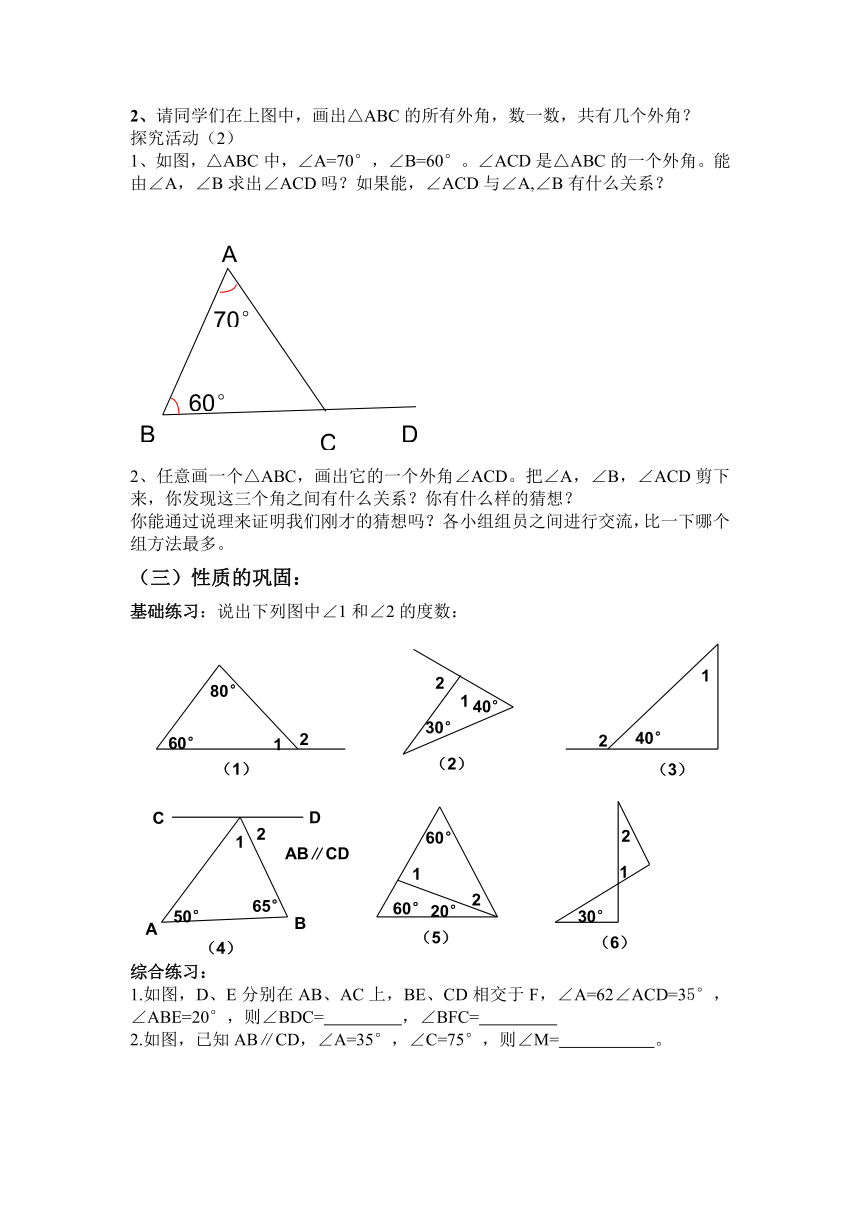
2、请同学们在上图中,画出△ABC的所有外角,数一数,共有几个外角?
探究活动(2)
1、如图,△ABC中,∠A=70°,∠B=60°。∠ACD是△ABC的一个外角。能由∠A,∠B求出∠ACD吗?如果能,∠ACD与∠A,∠B有什么关系?
2、任意画一个△ABC,画出它的一个外角∠ACD。把∠A,∠B,∠ACD剪下来,你发现这三个角之间有什么关系?你有什么样的猜想?
你能通过说理来证明我们刚才的猜想吗?各小组组员之间进行交流,比一下哪个组方法最多。
(三)性质的巩固:
基础练习:说出下列图中∠1和∠2的度数:
综合练习:
1.如图,D、E分别在AB、AC上,BE、CD相交于F,∠A=62∠ACD=35°,∠ABE=20°,则∠BDC= ,∠BFC=
2.如图,已知AB∥CD,∠A=35°,∠C=75°,则∠M= 。
1题图 2题图
3.如图,△ABC中,D为AC上一点,P为BD上一点,连接PC,则∠1、∠2、∠A的大小关系为 (用“﹤”符号表示)。
4.如图,DE交△ABC的边AB、AC于D、E,交BC延长线于F,∠B=67°,∠ACB=74°,∠AED=48°,则∠BDF=
3题图 4题图
(四)性质的应用
你是一个合格的检验员吗?
有一个零件的形状如图,按规定∠A=100°,∠B=20°,∠C=30°。现在量得 ∠CDB=152°,你认为这个零件合格吗?为什么?你有几种检验的方法?
(五)分享你我收获
(1)本节课你学到了什么?
(2)你有什么感悟?
(3)你有什么困惑?
(六)拓展数学天地
1、如图:∠BAE, ∠CBE, ∠ACD是△ABC 的外角,它们的和是多少?你有几种解题方法?
A
B
C
D
A
C
B
D
60°
70°
80°
60°
50°
1
40°
30°
40°
30°
(1)
(2)
(3)
(4)
(5)
(6)
65°
60°
60°
20°
AB∥CD
C
D
A
B
1
2
1
2
1
2
2
1
2
2
1
A
C
B
D
E
F
A
B
C
D
M
E
F
A
A
B
C
D
1
2
P
B
C
D
E
A
B
C
D
A
C
B
E
D
F
教学目标
知识技能目标
三角形的外角的概念及性质;
情感体验目标
通过探索三角形的外角的性质的活动,培养学生的论证能力,拓宽他们的解题思路,从而使他们灵活应用所学的知识。
创新性目标
在体验一题多变、一题多解的过程中发散思维,提高空间想象能力。
重点与难点
教学重点:(1)了解三角形的外角的概念和性质;
(2)能利用三角形的外角的性质解决简单的实际问题。
教学难点:(1)能够证明“三角形的外角的性质;
(2)运用三角形的外角的性质解决简单的实际问题。
教法与学法
教法:按照学生的认知规律,遵循以“学生为主体,教师为主导,活动为主线”的指导思想,采用以实验观察、教师引导的教学方法。
学法:学生以自主探究为主、合作交流为辅的方法进行学习;发现学习和接受学习相结合。
教学过程
感知身边的数学
你是一个合格的检验员吗?
有一个零件的形状如图,按规定∠A=100°,∠B=20°,∠C=30°。现在量得 ∠CDB=152°,你认为这个零件合格吗?为什么?
(二)探究新知
探究活动(1)
1、请同学们在草稿纸上画一个三角形,然后把它的一边延长,得到如图所示中的∠ACD。
问题1:这个角是三角形的内角吗?
问题2:∠ACD 的特点有哪些?(从顶点和角的两边两方面思考)
2、请同学们在上图中,画出△ABC的所有外角,数一数,共有几个外角?
探究活动(2)
1、如图,△ABC中,∠A=70°,∠B=60°。∠ACD是△ABC的一个外角。能由∠A,∠B求出∠ACD吗?如果能,∠ACD与∠A,∠B有什么关系?
2、任意画一个△ABC,画出它的一个外角∠ACD。把∠A,∠B,∠ACD剪下来,你发现这三个角之间有什么关系?你有什么样的猜想?
你能通过说理来证明我们刚才的猜想吗?各小组组员之间进行交流,比一下哪个组方法最多。
(三)性质的巩固:
基础练习:说出下列图中∠1和∠2的度数:
综合练习:
1.如图,D、E分别在AB、AC上,BE、CD相交于F,∠A=62∠ACD=35°,∠ABE=20°,则∠BDC= ,∠BFC=
2.如图,已知AB∥CD,∠A=35°,∠C=75°,则∠M= 。
1题图 2题图
3.如图,△ABC中,D为AC上一点,P为BD上一点,连接PC,则∠1、∠2、∠A的大小关系为 (用“﹤”符号表示)。
4.如图,DE交△ABC的边AB、AC于D、E,交BC延长线于F,∠B=67°,∠ACB=74°,∠AED=48°,则∠BDF=
3题图 4题图
(四)性质的应用
你是一个合格的检验员吗?
有一个零件的形状如图,按规定∠A=100°,∠B=20°,∠C=30°。现在量得 ∠CDB=152°,你认为这个零件合格吗?为什么?你有几种检验的方法?
(五)分享你我收获
(1)本节课你学到了什么?
(2)你有什么感悟?
(3)你有什么困惑?
(六)拓展数学天地
1、如图:∠BAE, ∠CBE, ∠ACD是△ABC 的外角,它们的和是多少?你有几种解题方法?
A
B
C
D
A
C
B
D
60°
70°
80°
60°
50°
1
40°
30°
40°
30°
(1)
(2)
(3)
(4)
(5)
(6)
65°
60°
60°
20°
AB∥CD
C
D
A
B
1
2
1
2
1
2
2
1
2
2
1
A
C
B
D
E
F
A
B
C
D
M
E
F
A
A
B
C
D
1
2
P
B
C
D
E
A
B
C
D
A
C
B
E
D
F
