河北省沧州市青县第二中学2020-2021学年八年级上学期期中数学试题(Word版,附答案解析)
文档属性
| 名称 | 河北省沧州市青县第二中学2020-2021学年八年级上学期期中数学试题(Word版,附答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 513.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 14:53:34 | ||
图片预览



文档简介
河北省沧州市青县第二中学2020-2021学年八年级上学期期中数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列长度的三条线段能组成三角形的是( )
A.1,2,3 B.2,2,4 C.3,4,5 D.3,4,8
2.对于下列各组条件,不能判定△≌△的一组是 ( )
A.∠A=∠,∠B=∠,AB= B.∠A=∠,AB=,AC=
C.∠A=∠,AB=,BC= D.AB=,AC=,BC=
3.等腰三角形的两边长是6cm和3cm,那么它的周长是
A.9cm B.12 cm C.12 cm或15 cm D.15 cm
4.在△ABC内取一点P使得点P到△ABC的三边距离相等,则点P应是△ABC的哪三条线交点 ( )
A.高 B.角平分线 C.中线 D.垂直平分线
5.下列几种说法 ①全等三角形的对应边相等;②面积相等的两个三角形全等;③周长相等的两个三角形全等;④全等的两个三角形的面积相等.其中正确的是( )
A.①② B.②③ C.③④ D.①④
6.下列判断中错误的是( )
A.有两角和一边对应相等的两个三角形全等
B.有两边和一角对应相等的两个三角形全等
C.有两边和其中一边上的中线对应相等的两个三角形全等
D.有一边对应相等的两个等边三角形全等
7.如图所示的正方形网格中,( )
A.330° B.315° C.310° D.320°
8.在RtΔABC中,∠ACB=90°,E是AB上一点,且BE=BC,过E作DE⊥AB交AC于D,如果AC=5cm,则AD+DE=( )
A.3 B.5 C.7 D.9
9.如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为( )
A.a=b B.2a+b=﹣1 C.2a﹣b=1 D.2a+b=1
10.如图, △DAC和△EBC均为等边三角形,A、C、B三点在同一直线上,AE、BD分别与CD、CE交于点M、N,有如下结论:① △ACE≌△DCB;②AC=DN;③AE=BD;④∠BOE=60°;其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.在△ABC中,已知∠A=60°,∠B=80°,则∠C的外角的度数是________.
12.如图所示,△ABC≌△ADE,若∠B=50°,∠EAB=155°,AE=5,则∠DAC=______ ,∠D= _____,AC=_____ .
13.如图,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2=_______.
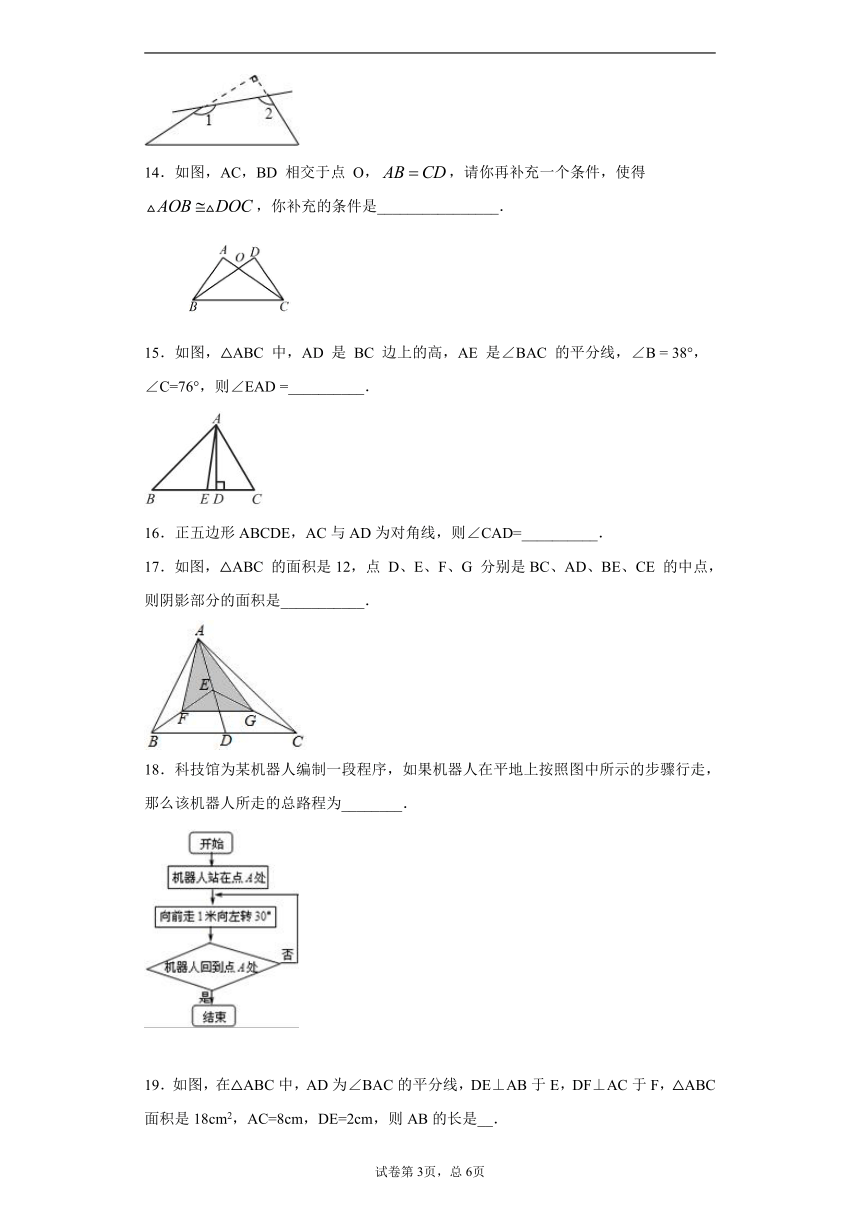
14.如图,AC,BD 相交于点 O,,请你再补充一个条件,使得 ,你补充的条件是________________.
15.如图,△ABC 中,AD 是 BC 边上的高,AE 是∠BAC 的平分线,∠B = 38°,∠C=76°,则∠EAD =__________.
16.正五边形ABCDE,AC与AD为对角线,则∠CAD=__________.
17.如图,△ABC 的面积是12,点 D、E、F、G 分别是BC、AD、BE、CE 的中点,则阴影部分的面积是___________.
18.科技馆为某机器人编制一段程序,如果机器人在平地上按照图中所示的步骤行走,那么该机器人所走的总路程为________.
19.如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是18cm2,AC=8cm,DE=2cm,则AB的长是__.
20.∠ACD是△的外角,的平分线与的平分线交于点,的平分线与的平分线交于点,…,的平分线与的平分线交于点An. 设∠A=.则=_________,∠A2021=____________.
三、解答题
21.如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E, ∠A=35°, ∠D=50°,求∠ACD的度数.
22.一个零件的形状如图,按规定∠A=90°,∠B=30°,∠C=10°,现测得∠BDC=132°,这个零件合格吗?为什么?
23.已知:如图,△ABC中,∠BAC=90°,AB=AC,D为AC上任一点,连接BD,过A点作BD的垂线交过C点与AB平行的直线CE于点E.求证:BD=AE.
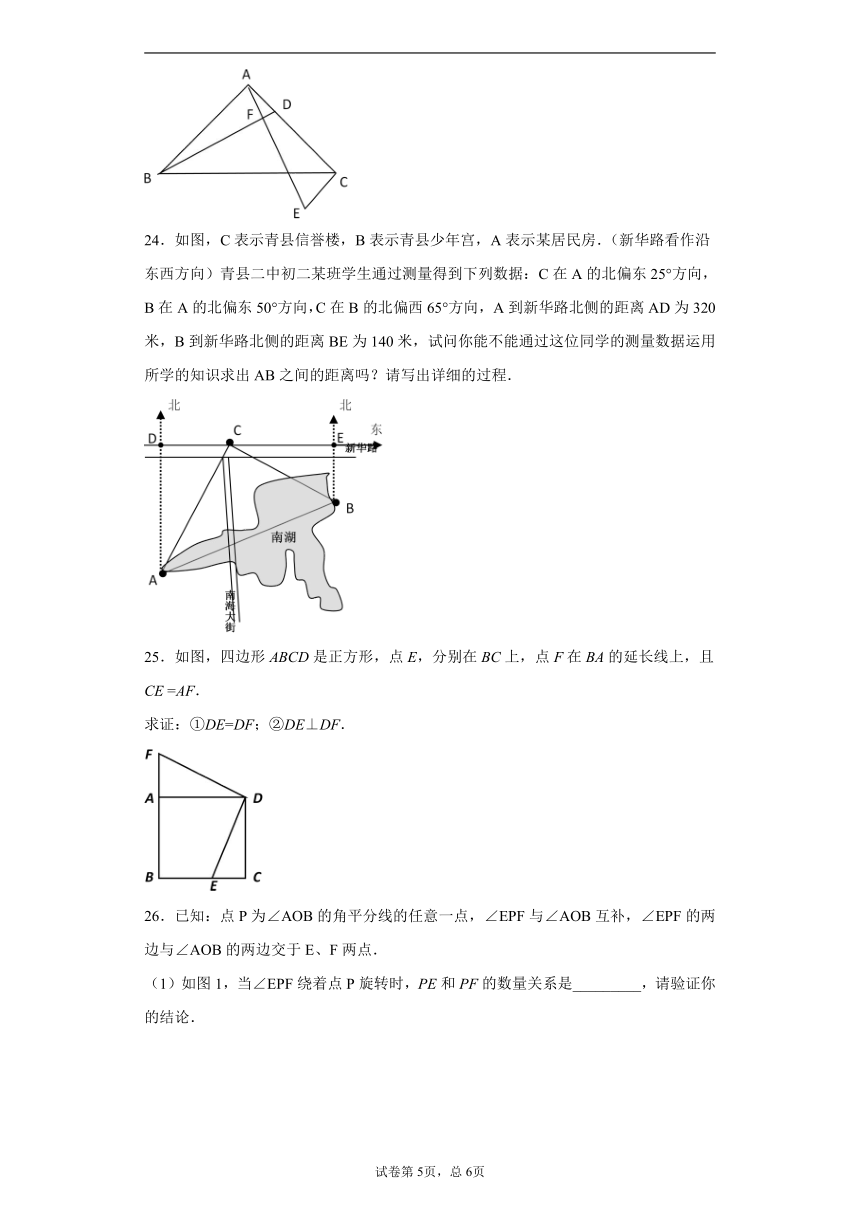
24.如图,C表示青县信誉楼,B表示青县少年宫,A表示某居民房.(新华路看作沿东西方向)青县二中初二某班学生通过测量得到下列数据:C在A的北偏东25°方向,B在A的北偏东50°方向,C在B的北偏西65°方向, A到新华路北侧的距离AD为320米,B到新华路北侧的距离BE为140米,试问你能不能通过这位同学的测量数据运用所学的知识求出AB之间的距离吗?请写出详细的过程.
25.如图,四边形ABCD是正方形,点E,分别在BC上,点F在BA的延长线上,且CE =AF.
求证:①DE=DF;②DE⊥DF.
26.已知:点P为∠AOB的角平分线的任意一点,∠EPF与∠AOB互补,∠EPF的两边与∠AOB的两边交于E、F两点.
(1)如图1,当∠EPF绕着点P旋转时,PE和PF的数量关系是_________,请验证你的结论.
(2)如图2,若∠AOB=90°时,∠EPF与∠AOB仍然互补,这时PE与PF还相等吗? 并加以证明.
参考答案
1.C
【解析】
A、1+2=3,不能构成三角形,故A错误;
B、2+2=4,不能构成三角形,故B错误;
C、3+4>5,能构成三角形,故C正确;
D、3+4<8,不能构成三角形,故D错误.
故选C.
2.C
【分析】
根据全等三角形的判定方法结合各选项提供的已知条件进行分析,从而得到答案
【详解】
解:A、∠A=∠A′,∠B=∠B′,AB=A′B′,正确,符合判定ASA;
B、∠A=∠A′,AB=A′B′,AC=A′C′,正确,符合判定SAS;
C、∠A=∠A′,AB=A′B′,BC=B′C′,不正确,其角不是两边的夹角;
D、AB=A′B′,AC=A′C′,BC=B′C′,正确,符合判定SSS.
故选:C.
【点睛】
本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS,直角三角形可用HL定理,但AAA、SSA,无法证明三角形全等.
3.D
【解析】
试题分析:题目给出等腰三角形有两条边长为6cm和3cm,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.
解:当腰为3cm时,3+3=6,不能构成三角形,因此这种情况不成立.
当腰为6cm时,6﹣3<6<6+3,能构成三角形;
此时等腰三角形的周长为6+6+3=15cm.
故选D.
考点:等腰三角形的性质;三角形三边关系.
4.B
【解析】
解:∵到三角形三边距离相等的点是三角形三条角平分线的交点,
∴点P应是△ABC的三条角平分线的交点.
故选B.
5.D
【分析】
根据全等三角形的性质对各小题分析判断即可得解.
【详解】
解:①全等三角形的对应边相等,正确;
②面积相等的两个三角形全等,错误;
③周长相等的两个三角形全等,错误;
④全等的两个三角形的面积相等,正确;
综上所述,正确的是①④.
故选:D.
【点睛】
本题考查了全等三角形的性质,是基础题,熟记性质是解题的关键.
6.B
【分析】
根据判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL进行分析即可.
【详解】
解:A、有两角和一边对应相等的两个三角形全等,说法正确;
B、有一边对应相等的两个等边三角形全等,说法正确;
C、有两边和其中一边上的中线对应相等的两个三角形全等,说法正确;
D、有两边和一角对应相等的两个三角形全等,说法错误;
故选D.
【点睛】
此题主要考查了三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
7.B
【分析】
根据正方形的轴对称性得∠1+∠7=90°,∠2+∠6=90°,∠3+∠5=90°,∠4=45°.
【详解】
解:由图可知,∠1所在的三角形与∠7所在的三角形全等,
可得,, ,,
则
故选B.
8.C
【分析】
根据HL证Rt△BED≌Rt△BCD,推出DE=DC,得出AD+DE=AD+DC=AC,代入求出即可.
【详解】
解:∵DE⊥AB,
∴∠DEB=90°=∠C,
在Rt△BED和Rt△BCD中
∴Rt△BED≌Rt△BCD(HL),
∴DE=DC,
∴AD+DE=AD+CD=AC=5cm,
故选:C.
【点睛】
本题考查了直角三角形全等的性质和判定,注意:全等三角形的对应边相等,判断直角三角形全等的方法有SAS,ASA,AAS,SSS,HL.
9.B
【解析】
试题分析:根据作图方法可得点P在第二象限角平分线上,
则P点横纵坐标的和为0,即2a+b+1=0,
∴2a+b=﹣1.故选B.
10.C
【分析】
由等边三角形的性质得到AC=CD,EC=BC,且∠ACD=∠ECB=60°,从而推出∠ACE=∠DCB,得到△ACE≌△DCB,可判断①;从而得到AE=BD,∠AEC=∠DBC,可判断③;再由三角形内角和可判断④;再由三角形中大边对大角进行分析可判断②.
【详解】
解:∵△DAC和△EBC都为等边三角形,
∴∠ACD=∠ECB=60°,AC=CD,EC=BC,
∴∠ACD+∠DCE=∠ECB+∠DCE,即∠ACE=∠DCB,
在△ACE和△DCB中,
,
∴△ACE≌△DCB(SAS),①正确;
∴AE=BD,∠AEC=∠DBC,③正确;
∵∠ACD=∠ECB=60°,∠DNE=∠CNB,
∴∠DCE=60°,∠BOE=∠BCE=60°,④正确;
∵AC=DC,
在△DNC中,DC所对的角为∠DNC=∠NCB+∠NBC=60°+∠NBC>60°,而DN所对的角为∠DCB=60°,根据三角形中等边对等角、大边对大角,小边对小角的规律,则DC>DN,即是AC>DN,所以②错误,
故选C.
【点睛】
此题考查了全等三角形的判定与性质,等边三角形的性质,三角形内角和,熟练掌握全等三角形的判定与性质是解本题的关键.
11.140°.
【解析】
∠C的外角=∠A+∠B=60°+80°=140°.故答案为140°.
12.155° 50° 5
【分析】
根据△ABC≌△ADE得到∠D=∠B,AE=AC,∠EAD=∠CAB,再由∠EAB=155°可得∠DAC.
【详解】
解:∵△ABC≌△ADE,
∴∠D=∠B=50°,AE=AC=5,∠EAD=∠CAB,
∴∠EAB=∠EAC+∠BAC=∠155°,
∴∠DAC=∠DAE+∠EAC=155°,
故答案为:155°;50°;5.
【点睛】
本题考查了全等三角形的性质,掌握全等三角形对应角和对应边相等是解题的关键.
13.:270°
【分析】
先根据三角形内角和定理算出∠3+∠4的度数,再根据四边形内角和为360°,计算出∠1+∠2的度数.
【详解】
∵在直角三角形中,
∴∠5=90°,
∴∠3+∠4=180°?90°=90°,
∵∠3+∠4+∠1+∠2=360°,
∴∠1+∠2=360°?90°=270°,
故答案是:270°.
【点睛】
本题主要考查三角形内角和定理以及四边形内角和定理,掌握四边形内角和为360°,是解题的关键.
14.
【分析】
添加∠A=∠D,再加上对顶角∠AOB=∠DOC,再有AB=CD可利用AAS判定△AOB≌△DOC.
【详解】
解:添加∠A=∠D,
∵在△ABO和△DCO中,
∠A=∠D,∠AOB=∠DOC, AB=CD;
∴△AOB≌△DOC(AAS),
故答案为∠A=∠D.
【点睛】
本题主要考查全等三角形的判定,解决本题的关键是要熟练掌握全等三角形的判定方法.
15.19°
【分析】
根据直角三角形两锐角互余求出∠BAD,根据三角形的内角和等于180°求出∠BAC的度数,然后根据角平分线的定义求出∠BAE,再求解即可.
【详解】
解:∵∠B=38°,∠C=76°,
∴∠BAC=180-38-76=66°,
∵AE是∠BAC平分线,
∴∠BAE=33°,
∵AD是BC边上的高,∠B=38°,
∴∠BAD=52°,
∴∠DAE=∠BAD-∠BAE=19°,
故答案为19°.
【点睛】
本题考查三角形内角和定理,角平分线的定义等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
16.36°
【分析】
根据正五边形的性质和内角和为540°,得到△ABC≌△AED,AC=AD,AB=BC=AE=ED,先求出∠BAC和∠DAE的度数,即可求出∠CAD的度数.
【详解】
解:根据正五边形的性质,△ABC≌△AED,
∴∠CAB=∠DAE=(180°-108°)=36°,
∴∠CAD=108°-36°-36°=36°.
故答案为:36°.
【点睛】
本题考查了正五边形的性质:各边相等,各角相等,内角和为540°.同时考查了多边形的内角和计算公式,及角相互间的和差关系,有一定的难度.
17.
【分析】
根据中线的性质,可得的面积的面积的面积的面积,的面积,根据三角形中位线的性质可得的面积的面积,进而得到的面积.
【详解】
解:点,,,分别是,,,的中点,
是的中线,是的中线,是的中线,是的中线,是的中线,
的面积的面积的面积的面积,
同理可得的面积,
的面积的面积,
又是的中位线,
∴FG∥BC,BC=2FG,
∴△EFG∽△EBC,相似比为1:2,
的面积的面积,
的面积是,
故答案为:.
【点睛】
本题主要考查了三角形的面积,解决问题的关键是掌握:三角形的中线将三角形分成面积相等的两部分.
18.12米
【解析】
试题分析:根据题意可得机器人每次都是旋转30°,则需要经过12次旋转才能回到起到,即所所走的总路程为12×1=12米.
考点:多边形的外角和性质.
19.10cm
【分析】
根据角平分线性质求出DE=DF=2cm,根据三角形面积公式列出方程求解即可.
【详解】
已知在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,
根据角平分线的性质可得DE=DF=2cm,
又因△ABC面积是18cm2,DE=2㎝,AC=8cm,
所以S△ABC=AB?DE+AC?DF=18,
即×AB×2+×8×2=18,
解得AB=10cm.
考点:角平分线的性质;三角形的面积.
20.
【分析】
据角平分线的定义可得∠A1BC=∠ABC,∠A1CD=∠ACD,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,整理即可求出∠A1的度数,同理求出∠A2,可以发现后一个角等于前一个角的,根据此规律即可得解.
【详解】
解:∵A1B是∠ABC的平分线,A1C是∠ACD的平分线,
∴∠A1BC=∠ABC,∠A1CD=∠ACD,
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,
∴(∠A+∠ABC)=∠ABC+∠A1,
∴∠A1=∠A,
∵∠A=,
∴∠A1=,
同理可得:∠An=,
∴∠A2021=,
故答案为:,.
【点睛】
本题考查了三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,熟记性质并准确识图然后求出后一个角是前一个角的是解题的关键.
21.83°.
【解析】
试题分析:由DF⊥AB,在Rt△BDF中可求得∠B;再由∠ACD=∠A+∠B可求得.
试题解析:∵DF⊥AB,
∴∠B+∠D=90°,
∴∠B=90°-∠D=90°-42°=48°,
∴∠ACD=∠A+∠B=35°+48°=83°.
22.不合格,理由见解析
【分析】
根据三角形外角的性质求出∠BDC的度数,与测量所得的度数对比即可得出结论.
【详解】
解:如图,∠CDE是△ADC的外角,∠BDE是△ABD的外角,
∵∠CDE=∠C+∠CAD,∠BDE=∠B+∠DAB,
∴∠BDC=∠CDE+∠BDE=∠C+∠CAD+∠B+∠DAB,
即∠BDC=∠B+∠C+∠A=30°+10°+90°=130°.
检验已量得∠BDC=132°,可判断这个零件不合格.
【点睛】
本题考查了三角形的外角性质,三角形的外角等于和它不相邻的两个内角的和.
23.见解析
【分析】
先证∠ABD=∠CAE,再证△ABD≌△CAE即可得出答案.
【详解】
证明:∵AB∥CE,
∴∠BAF=∠AEC,∠BAC+∠ACE=180°,
∵∠BAC=90°,
∴∠ACE=90°,
∵AF⊥BD,
∴∠ABD+∠BAF=90°,∠EAC+∠BAF=90°,
∴∠ABD=∠CAE
在△ABD和△CAE中,
∴△ABD≌△CAE(AAS)
∴BD=AE.
【点睛】
本题考查全等三角形的判定和性质,难度不大,注意利用全等三角形的知识证明线段的相等.
24.能,AB=460米,理由见解析
【分析】
过C作CM⊥AB于M,分别证明Rt△ACD≌Rt△ACM,Rt△CEB≌Rt△CMB,得到AD=AM=320,BE=BM=140,从而得到AB的长度.
【详解】
解:由题意可得:如图:过C作CM⊥AB于M,
∠CAD=25°,∠DAB=50°,∠CBE=65°,AD=320,BE=140,∠ADC=∠CEB=90°,
则AC平分∠DAB,
∵CD⊥AD,
∴CD=CM,
又∵AC=AC,
∴Rt△ACD≌Rt△ACM(HL),
∴AD=AM=320,
∵∠DAB=50°,
∴∠ABE=180°-50°=130°,
∴∠ABC=65°=∠CBE,
同理,Rt△CEB≌Rt△CMB,
∴BE=BM=140,
∴AB=AM+BM=460,
∴AB之间的距离为460米.
【点睛】
本题考查了全等三角形的判定和性质,角平分线的性质,解题的关键是添加辅助线CM,证明三角形全等.
25.①见解析;②见解析
【分析】
①根据正方形性质求出AD=DC,∠FAD=∠DCE=90°,根据全等三角形判定推出即可;
②根据全等得出∠FDA=∠CDE,求出∠FDE=∠FDA+∠ADE=∠ADC=90°即可;
【详解】
解:①证明:∵四边形ABCD是正方形,
∴AD=DC,∠FAD=∠DCE=90°,
在△FAD和△ECD中,
,
∴△FAD≌△ECD(SAS),
∴DE=DF;
②∵四边形ABCD是正方形,
∴∠ADC=90°,
∵△FAD≌△ECD,
∴∠FDA=∠CDE,
∴∠FDE=∠FDA+∠ADE=∠CDE+∠ADE=∠ADC=90°,
∴DE⊥DF.
【点睛】
本题考查了全等三角形的性质和判定,正方形性质的应用,主要考查学生的推理能力.
26.(1)见解析;(2)见解析
【分析】
(1)结论:PE=PF;作PG⊥OA于G,PH⊥OB于H.只要证明△OPG≌△OPH,△PGE≌△PHF,即可解决问题;
(2)结论:PE=PF;作PG⊥OA于G,PH⊥OB于H.只要证明△OPG≌△OPH,△PGE≌△PHF,即可解决问题;
【详解】
解:(1)PE=PF,
理由:作PG⊥OA于G,PH⊥OB于H.
在△OPG和△OPH中,
,
∴△OPG≌△OPH,
∴PG=PH,
∵∠AOB=50°,∠PGO=∠PHO=90°,
∴∠GPH=130°,
∵∠EPF=130°,
∴∠GPH=∠EPF,
∴∠GPE=∠FPH,
在△PGE和△PHF中,
,
∴△PGE≌△PHF,
∴PE=PF.
(2)PE=PF;
理由:作PG⊥OA于G,PH⊥OB于H.
∵∠PGO=∠GOH=∠PHO=90°,
∴∠HPG=∠EPF=90°,
∴∠EPG=∠FPH,
∵OC平分∠AOB,PG⊥OA,PH⊥OB,
∴∠POG=∠POH,
在△OPG和△OPH中,
,
∴△OPG≌△OPH,
∴PG=PH,
在△PGE和△PHF中,
,
∴△PGE≌△PHF,
∴PE=PF.
【点睛】
本题考查几何变换综合题,全等三角形的判定和性质、角平分线的定义等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用两次全等三角形解决问题.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列长度的三条线段能组成三角形的是( )
A.1,2,3 B.2,2,4 C.3,4,5 D.3,4,8
2.对于下列各组条件,不能判定△≌△的一组是 ( )
A.∠A=∠,∠B=∠,AB= B.∠A=∠,AB=,AC=
C.∠A=∠,AB=,BC= D.AB=,AC=,BC=
3.等腰三角形的两边长是6cm和3cm,那么它的周长是
A.9cm B.12 cm C.12 cm或15 cm D.15 cm
4.在△ABC内取一点P使得点P到△ABC的三边距离相等,则点P应是△ABC的哪三条线交点 ( )
A.高 B.角平分线 C.中线 D.垂直平分线
5.下列几种说法 ①全等三角形的对应边相等;②面积相等的两个三角形全等;③周长相等的两个三角形全等;④全等的两个三角形的面积相等.其中正确的是( )
A.①② B.②③ C.③④ D.①④
6.下列判断中错误的是( )
A.有两角和一边对应相等的两个三角形全等
B.有两边和一角对应相等的两个三角形全等
C.有两边和其中一边上的中线对应相等的两个三角形全等
D.有一边对应相等的两个等边三角形全等
7.如图所示的正方形网格中,( )
A.330° B.315° C.310° D.320°
8.在RtΔABC中,∠ACB=90°,E是AB上一点,且BE=BC,过E作DE⊥AB交AC于D,如果AC=5cm,则AD+DE=( )
A.3 B.5 C.7 D.9
9.如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为( )
A.a=b B.2a+b=﹣1 C.2a﹣b=1 D.2a+b=1
10.如图, △DAC和△EBC均为等边三角形,A、C、B三点在同一直线上,AE、BD分别与CD、CE交于点M、N,有如下结论:① △ACE≌△DCB;②AC=DN;③AE=BD;④∠BOE=60°;其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.在△ABC中,已知∠A=60°,∠B=80°,则∠C的外角的度数是________.
12.如图所示,△ABC≌△ADE,若∠B=50°,∠EAB=155°,AE=5,则∠DAC=______ ,∠D= _____,AC=_____ .
13.如图,一个直角三角形纸片,剪去直角后,得到一个四边形,则∠1+∠2=_______.
14.如图,AC,BD 相交于点 O,,请你再补充一个条件,使得 ,你补充的条件是________________.
15.如图,△ABC 中,AD 是 BC 边上的高,AE 是∠BAC 的平分线,∠B = 38°,∠C=76°,则∠EAD =__________.
16.正五边形ABCDE,AC与AD为对角线,则∠CAD=__________.
17.如图,△ABC 的面积是12,点 D、E、F、G 分别是BC、AD、BE、CE 的中点,则阴影部分的面积是___________.
18.科技馆为某机器人编制一段程序,如果机器人在平地上按照图中所示的步骤行走,那么该机器人所走的总路程为________.
19.如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是18cm2,AC=8cm,DE=2cm,则AB的长是__.
20.∠ACD是△的外角,的平分线与的平分线交于点,的平分线与的平分线交于点,…,的平分线与的平分线交于点An. 设∠A=.则=_________,∠A2021=____________.
三、解答题
21.如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E, ∠A=35°, ∠D=50°,求∠ACD的度数.
22.一个零件的形状如图,按规定∠A=90°,∠B=30°,∠C=10°,现测得∠BDC=132°,这个零件合格吗?为什么?
23.已知:如图,△ABC中,∠BAC=90°,AB=AC,D为AC上任一点,连接BD,过A点作BD的垂线交过C点与AB平行的直线CE于点E.求证:BD=AE.
24.如图,C表示青县信誉楼,B表示青县少年宫,A表示某居民房.(新华路看作沿东西方向)青县二中初二某班学生通过测量得到下列数据:C在A的北偏东25°方向,B在A的北偏东50°方向,C在B的北偏西65°方向, A到新华路北侧的距离AD为320米,B到新华路北侧的距离BE为140米,试问你能不能通过这位同学的测量数据运用所学的知识求出AB之间的距离吗?请写出详细的过程.
25.如图,四边形ABCD是正方形,点E,分别在BC上,点F在BA的延长线上,且CE =AF.
求证:①DE=DF;②DE⊥DF.
26.已知:点P为∠AOB的角平分线的任意一点,∠EPF与∠AOB互补,∠EPF的两边与∠AOB的两边交于E、F两点.
(1)如图1,当∠EPF绕着点P旋转时,PE和PF的数量关系是_________,请验证你的结论.
(2)如图2,若∠AOB=90°时,∠EPF与∠AOB仍然互补,这时PE与PF还相等吗? 并加以证明.
参考答案
1.C
【解析】
A、1+2=3,不能构成三角形,故A错误;
B、2+2=4,不能构成三角形,故B错误;
C、3+4>5,能构成三角形,故C正确;
D、3+4<8,不能构成三角形,故D错误.
故选C.
2.C
【分析】
根据全等三角形的判定方法结合各选项提供的已知条件进行分析,从而得到答案
【详解】
解:A、∠A=∠A′,∠B=∠B′,AB=A′B′,正确,符合判定ASA;
B、∠A=∠A′,AB=A′B′,AC=A′C′,正确,符合判定SAS;
C、∠A=∠A′,AB=A′B′,BC=B′C′,不正确,其角不是两边的夹角;
D、AB=A′B′,AC=A′C′,BC=B′C′,正确,符合判定SSS.
故选:C.
【点睛】
本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS,直角三角形可用HL定理,但AAA、SSA,无法证明三角形全等.
3.D
【解析】
试题分析:题目给出等腰三角形有两条边长为6cm和3cm,而没有明确腰、底分别是多少,所以要进行讨论,还要应用三角形的三边关系验证能否组成三角形.
解:当腰为3cm时,3+3=6,不能构成三角形,因此这种情况不成立.
当腰为6cm时,6﹣3<6<6+3,能构成三角形;
此时等腰三角形的周长为6+6+3=15cm.
故选D.
考点:等腰三角形的性质;三角形三边关系.
4.B
【解析】
解:∵到三角形三边距离相等的点是三角形三条角平分线的交点,
∴点P应是△ABC的三条角平分线的交点.
故选B.
5.D
【分析】
根据全等三角形的性质对各小题分析判断即可得解.
【详解】
解:①全等三角形的对应边相等,正确;
②面积相等的两个三角形全等,错误;
③周长相等的两个三角形全等,错误;
④全等的两个三角形的面积相等,正确;
综上所述,正确的是①④.
故选:D.
【点睛】
本题考查了全等三角形的性质,是基础题,熟记性质是解题的关键.
6.B
【分析】
根据判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL进行分析即可.
【详解】
解:A、有两角和一边对应相等的两个三角形全等,说法正确;
B、有一边对应相等的两个等边三角形全等,说法正确;
C、有两边和其中一边上的中线对应相等的两个三角形全等,说法正确;
D、有两边和一角对应相等的两个三角形全等,说法错误;
故选D.
【点睛】
此题主要考查了三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
7.B
【分析】
根据正方形的轴对称性得∠1+∠7=90°,∠2+∠6=90°,∠3+∠5=90°,∠4=45°.
【详解】
解:由图可知,∠1所在的三角形与∠7所在的三角形全等,
可得,, ,,
则
故选B.
8.C
【分析】
根据HL证Rt△BED≌Rt△BCD,推出DE=DC,得出AD+DE=AD+DC=AC,代入求出即可.
【详解】
解:∵DE⊥AB,
∴∠DEB=90°=∠C,
在Rt△BED和Rt△BCD中
∴Rt△BED≌Rt△BCD(HL),
∴DE=DC,
∴AD+DE=AD+CD=AC=5cm,
故选:C.
【点睛】
本题考查了直角三角形全等的性质和判定,注意:全等三角形的对应边相等,判断直角三角形全等的方法有SAS,ASA,AAS,SSS,HL.
9.B
【解析】
试题分析:根据作图方法可得点P在第二象限角平分线上,
则P点横纵坐标的和为0,即2a+b+1=0,
∴2a+b=﹣1.故选B.
10.C
【分析】
由等边三角形的性质得到AC=CD,EC=BC,且∠ACD=∠ECB=60°,从而推出∠ACE=∠DCB,得到△ACE≌△DCB,可判断①;从而得到AE=BD,∠AEC=∠DBC,可判断③;再由三角形内角和可判断④;再由三角形中大边对大角进行分析可判断②.
【详解】
解:∵△DAC和△EBC都为等边三角形,
∴∠ACD=∠ECB=60°,AC=CD,EC=BC,
∴∠ACD+∠DCE=∠ECB+∠DCE,即∠ACE=∠DCB,
在△ACE和△DCB中,
,
∴△ACE≌△DCB(SAS),①正确;
∴AE=BD,∠AEC=∠DBC,③正确;
∵∠ACD=∠ECB=60°,∠DNE=∠CNB,
∴∠DCE=60°,∠BOE=∠BCE=60°,④正确;
∵AC=DC,
在△DNC中,DC所对的角为∠DNC=∠NCB+∠NBC=60°+∠NBC>60°,而DN所对的角为∠DCB=60°,根据三角形中等边对等角、大边对大角,小边对小角的规律,则DC>DN,即是AC>DN,所以②错误,
故选C.
【点睛】
此题考查了全等三角形的判定与性质,等边三角形的性质,三角形内角和,熟练掌握全等三角形的判定与性质是解本题的关键.
11.140°.
【解析】
∠C的外角=∠A+∠B=60°+80°=140°.故答案为140°.
12.155° 50° 5
【分析】
根据△ABC≌△ADE得到∠D=∠B,AE=AC,∠EAD=∠CAB,再由∠EAB=155°可得∠DAC.
【详解】
解:∵△ABC≌△ADE,
∴∠D=∠B=50°,AE=AC=5,∠EAD=∠CAB,
∴∠EAB=∠EAC+∠BAC=∠155°,
∴∠DAC=∠DAE+∠EAC=155°,
故答案为:155°;50°;5.
【点睛】
本题考查了全等三角形的性质,掌握全等三角形对应角和对应边相等是解题的关键.
13.:270°
【分析】
先根据三角形内角和定理算出∠3+∠4的度数,再根据四边形内角和为360°,计算出∠1+∠2的度数.
【详解】
∵在直角三角形中,
∴∠5=90°,
∴∠3+∠4=180°?90°=90°,
∵∠3+∠4+∠1+∠2=360°,
∴∠1+∠2=360°?90°=270°,
故答案是:270°.
【点睛】
本题主要考查三角形内角和定理以及四边形内角和定理,掌握四边形内角和为360°,是解题的关键.
14.
【分析】
添加∠A=∠D,再加上对顶角∠AOB=∠DOC,再有AB=CD可利用AAS判定△AOB≌△DOC.
【详解】
解:添加∠A=∠D,
∵在△ABO和△DCO中,
∠A=∠D,∠AOB=∠DOC, AB=CD;
∴△AOB≌△DOC(AAS),
故答案为∠A=∠D.
【点睛】
本题主要考查全等三角形的判定,解决本题的关键是要熟练掌握全等三角形的判定方法.
15.19°
【分析】
根据直角三角形两锐角互余求出∠BAD,根据三角形的内角和等于180°求出∠BAC的度数,然后根据角平分线的定义求出∠BAE,再求解即可.
【详解】
解:∵∠B=38°,∠C=76°,
∴∠BAC=180-38-76=66°,
∵AE是∠BAC平分线,
∴∠BAE=33°,
∵AD是BC边上的高,∠B=38°,
∴∠BAD=52°,
∴∠DAE=∠BAD-∠BAE=19°,
故答案为19°.
【点睛】
本题考查三角形内角和定理,角平分线的定义等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
16.36°
【分析】
根据正五边形的性质和内角和为540°,得到△ABC≌△AED,AC=AD,AB=BC=AE=ED,先求出∠BAC和∠DAE的度数,即可求出∠CAD的度数.
【详解】
解:根据正五边形的性质,△ABC≌△AED,
∴∠CAB=∠DAE=(180°-108°)=36°,
∴∠CAD=108°-36°-36°=36°.
故答案为:36°.
【点睛】
本题考查了正五边形的性质:各边相等,各角相等,内角和为540°.同时考查了多边形的内角和计算公式,及角相互间的和差关系,有一定的难度.
17.
【分析】
根据中线的性质,可得的面积的面积的面积的面积,的面积,根据三角形中位线的性质可得的面积的面积,进而得到的面积.
【详解】
解:点,,,分别是,,,的中点,
是的中线,是的中线,是的中线,是的中线,是的中线,
的面积的面积的面积的面积,
同理可得的面积,
的面积的面积,
又是的中位线,
∴FG∥BC,BC=2FG,
∴△EFG∽△EBC,相似比为1:2,
的面积的面积,
的面积是,
故答案为:.
【点睛】
本题主要考查了三角形的面积,解决问题的关键是掌握:三角形的中线将三角形分成面积相等的两部分.
18.12米
【解析】
试题分析:根据题意可得机器人每次都是旋转30°,则需要经过12次旋转才能回到起到,即所所走的总路程为12×1=12米.
考点:多边形的外角和性质.
19.10cm
【分析】
根据角平分线性质求出DE=DF=2cm,根据三角形面积公式列出方程求解即可.
【详解】
已知在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,
根据角平分线的性质可得DE=DF=2cm,
又因△ABC面积是18cm2,DE=2㎝,AC=8cm,
所以S△ABC=AB?DE+AC?DF=18,
即×AB×2+×8×2=18,
解得AB=10cm.
考点:角平分线的性质;三角形的面积.
20.
【分析】
据角平分线的定义可得∠A1BC=∠ABC,∠A1CD=∠ACD,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,整理即可求出∠A1的度数,同理求出∠A2,可以发现后一个角等于前一个角的,根据此规律即可得解.
【详解】
解:∵A1B是∠ABC的平分线,A1C是∠ACD的平分线,
∴∠A1BC=∠ABC,∠A1CD=∠ACD,
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,
∴(∠A+∠ABC)=∠ABC+∠A1,
∴∠A1=∠A,
∵∠A=,
∴∠A1=,
同理可得:∠An=,
∴∠A2021=,
故答案为:,.
【点睛】
本题考查了三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,熟记性质并准确识图然后求出后一个角是前一个角的是解题的关键.
21.83°.
【解析】
试题分析:由DF⊥AB,在Rt△BDF中可求得∠B;再由∠ACD=∠A+∠B可求得.
试题解析:∵DF⊥AB,
∴∠B+∠D=90°,
∴∠B=90°-∠D=90°-42°=48°,
∴∠ACD=∠A+∠B=35°+48°=83°.
22.不合格,理由见解析
【分析】
根据三角形外角的性质求出∠BDC的度数,与测量所得的度数对比即可得出结论.
【详解】
解:如图,∠CDE是△ADC的外角,∠BDE是△ABD的外角,
∵∠CDE=∠C+∠CAD,∠BDE=∠B+∠DAB,
∴∠BDC=∠CDE+∠BDE=∠C+∠CAD+∠B+∠DAB,
即∠BDC=∠B+∠C+∠A=30°+10°+90°=130°.
检验已量得∠BDC=132°,可判断这个零件不合格.
【点睛】
本题考查了三角形的外角性质,三角形的外角等于和它不相邻的两个内角的和.
23.见解析
【分析】
先证∠ABD=∠CAE,再证△ABD≌△CAE即可得出答案.
【详解】
证明:∵AB∥CE,
∴∠BAF=∠AEC,∠BAC+∠ACE=180°,
∵∠BAC=90°,
∴∠ACE=90°,
∵AF⊥BD,
∴∠ABD+∠BAF=90°,∠EAC+∠BAF=90°,
∴∠ABD=∠CAE
在△ABD和△CAE中,
∴△ABD≌△CAE(AAS)
∴BD=AE.
【点睛】
本题考查全等三角形的判定和性质,难度不大,注意利用全等三角形的知识证明线段的相等.
24.能,AB=460米,理由见解析
【分析】
过C作CM⊥AB于M,分别证明Rt△ACD≌Rt△ACM,Rt△CEB≌Rt△CMB,得到AD=AM=320,BE=BM=140,从而得到AB的长度.
【详解】
解:由题意可得:如图:过C作CM⊥AB于M,
∠CAD=25°,∠DAB=50°,∠CBE=65°,AD=320,BE=140,∠ADC=∠CEB=90°,
则AC平分∠DAB,
∵CD⊥AD,
∴CD=CM,
又∵AC=AC,
∴Rt△ACD≌Rt△ACM(HL),
∴AD=AM=320,
∵∠DAB=50°,
∴∠ABE=180°-50°=130°,
∴∠ABC=65°=∠CBE,
同理,Rt△CEB≌Rt△CMB,
∴BE=BM=140,
∴AB=AM+BM=460,
∴AB之间的距离为460米.
【点睛】
本题考查了全等三角形的判定和性质,角平分线的性质,解题的关键是添加辅助线CM,证明三角形全等.
25.①见解析;②见解析
【分析】
①根据正方形性质求出AD=DC,∠FAD=∠DCE=90°,根据全等三角形判定推出即可;
②根据全等得出∠FDA=∠CDE,求出∠FDE=∠FDA+∠ADE=∠ADC=90°即可;
【详解】
解:①证明:∵四边形ABCD是正方形,
∴AD=DC,∠FAD=∠DCE=90°,
在△FAD和△ECD中,
,
∴△FAD≌△ECD(SAS),
∴DE=DF;
②∵四边形ABCD是正方形,
∴∠ADC=90°,
∵△FAD≌△ECD,
∴∠FDA=∠CDE,
∴∠FDE=∠FDA+∠ADE=∠CDE+∠ADE=∠ADC=90°,
∴DE⊥DF.
【点睛】
本题考查了全等三角形的性质和判定,正方形性质的应用,主要考查学生的推理能力.
26.(1)见解析;(2)见解析
【分析】
(1)结论:PE=PF;作PG⊥OA于G,PH⊥OB于H.只要证明△OPG≌△OPH,△PGE≌△PHF,即可解决问题;
(2)结论:PE=PF;作PG⊥OA于G,PH⊥OB于H.只要证明△OPG≌△OPH,△PGE≌△PHF,即可解决问题;
【详解】
解:(1)PE=PF,
理由:作PG⊥OA于G,PH⊥OB于H.
在△OPG和△OPH中,
,
∴△OPG≌△OPH,
∴PG=PH,
∵∠AOB=50°,∠PGO=∠PHO=90°,
∴∠GPH=130°,
∵∠EPF=130°,
∴∠GPH=∠EPF,
∴∠GPE=∠FPH,
在△PGE和△PHF中,
,
∴△PGE≌△PHF,
∴PE=PF.
(2)PE=PF;
理由:作PG⊥OA于G,PH⊥OB于H.
∵∠PGO=∠GOH=∠PHO=90°,
∴∠HPG=∠EPF=90°,
∴∠EPG=∠FPH,
∵OC平分∠AOB,PG⊥OA,PH⊥OB,
∴∠POG=∠POH,
在△OPG和△OPH中,
,
∴△OPG≌△OPH,
∴PG=PH,
在△PGE和△PHF中,
,
∴△PGE≌△PHF,
∴PE=PF.
【点睛】
本题考查几何变换综合题,全等三角形的判定和性质、角平分线的定义等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用两次全等三角形解决问题.
同课章节目录
