河北省邯郸市永年区2020-2021学年八年级上学期期中数学试题(Word版,附答案解析)
文档属性
| 名称 | 河北省邯郸市永年区2020-2021学年八年级上学期期中数学试题(Word版,附答案解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 643.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:00:00 | ||
图片预览





文档简介
河北省邯郸市永年区2020-2021学年八年级上学期期中数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若分式的值为0,则x的值是( )
A.±3 B.﹣3 C.3 D.0
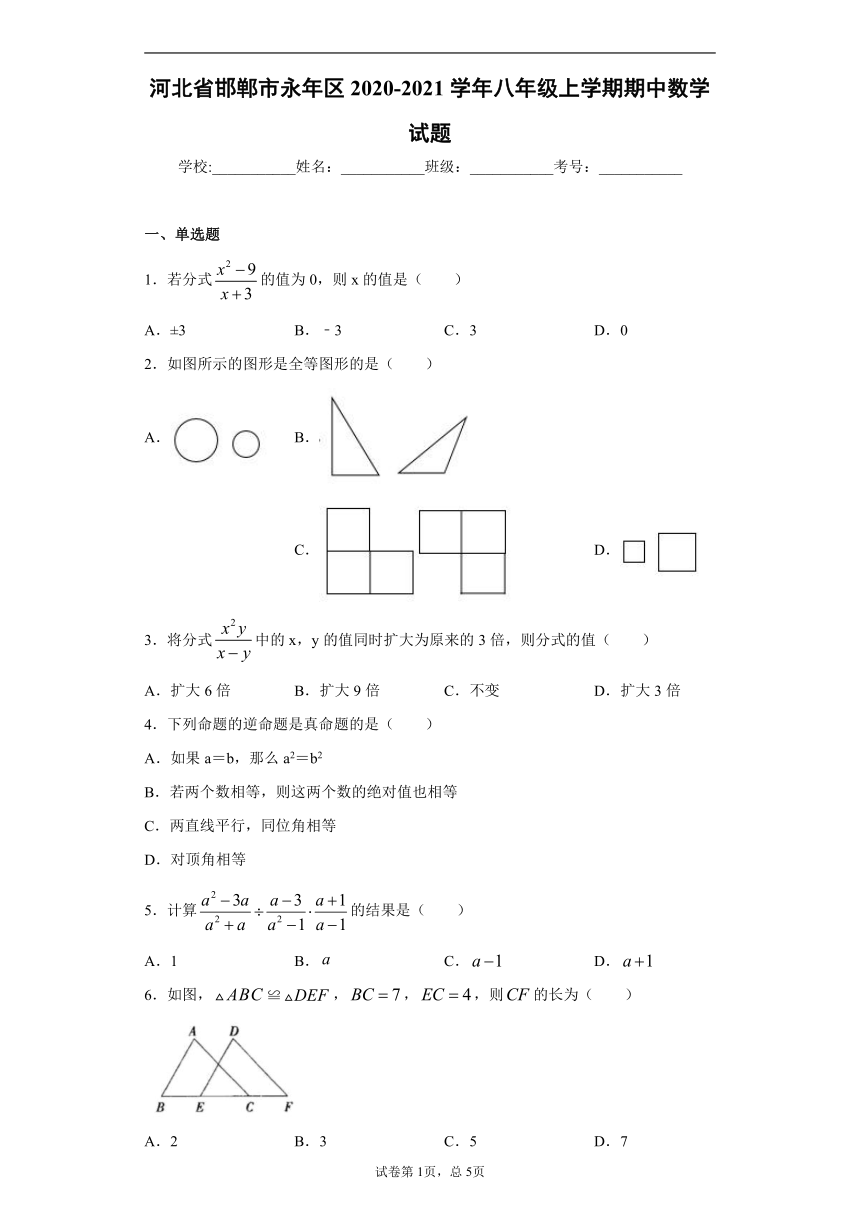
2.如图所示的图形是全等图形的是( )
A. B. C. D.
3.将分式中的x,y的值同时扩大为原来的3倍,则分式的值( )
A.扩大6倍 B.扩大9倍 C.不变 D.扩大3倍
4.下列命题的逆命题是真命题的是( )
A.如果a=b,那么a2=b2
B.若两个数相等,则这两个数的绝对值也相等
C.两直线平行,同位角相等
D.对顶角相等
5.计算的结果是( )
A.1 B. C. D.
6.如图,≌,,,则的长为( )
A.2 B.3 C.5 D.7
7.化简的结果是( )
A. B. C. D.
8.如图,已知,要使,只需要添加一个条件是( )
A. B. C. D.
9.若分式运算的结果为x,则在□中添加的运算符号为( )
A.+ B.-或÷ C.-或÷ D.+或×
10.下列各图中,为三角形的边长,则甲,乙、丙三个三角形和左侧全等的是( )
A.甲和乙 B.只有乙 C.甲和丙 D.乙和丙
11.若关于x的分式方程有增根,则的值是( )
A. B. C.3 D.
12.一个三角形的三边长分别为2,5,x,另一个三角形的三边长分别为y,2,6,若这两个三角形全等,则x+y=( )
A.11 B.7 C.8 D.13
13.是分式方程的解,则a的值是( )
A. B.0 C.1 D.3
14.下面“作一个角等于已知角”的尺规作图过程.已知:,求作:一个角,使它等于.作法:如图
(1)作射线;
(2)以为圆心﹐任意长为半径作孤,交于,交于;
(3)以为圆心,为半径作弧,交于;
(4)以为圆心,为半径作弧﹐交弧于;
(5)过点作射线.
则就是所求作的角.
请回答:该作图的依据是( )
A. B. C. D.
15.某班学生到距学校12km的烈士陵园扫墓,一部分同学骑自行车先行,经h后,其余同学乘汽车出发,由于□□□□□□,设自行车的速度为xkm/h,则可得方程为,根据此情境和所列方程,上题中□□□□□□表示被墨水污损部分的内容,其内容应该是( )
A.汽车速度是自行车速度的3倍,结果同时到达
B.汽车速度是自行车速度的3倍,后部分同学比前部分同学迟到h
C.汽车速度是自行车速度的3倍,前部分同学比后部分同学迟到h
D.汽车速度比自行车速度每小时多3km,结果同时到达
16.如图,在中,,的角平分线,相交于点,过点作交的延长线于点,交于点.则下列结论:①;②;③;④连接,平分.其中正确的是( ).
A.①②③ B.①②④ C.①③④ D.①②③④
二、填空题
17.当x=_____时,分式与分式的值互为相反数.
18.甲、乙两辆汽车同时从地出发,开往相距的地,甲、乙两车的速度之比是,结果乙车比甲车早分钟到达地,则甲车的速度为_____.
19.如图,给出下列结论:①;②;③;④.其中正确的有_______(填写答案序号).
三、解答题
20.尺规作图:已知和线段,求作,使.(作图痕迹要清晰规范,不要求作图步骤)
21.计算下列各式:
(1)
(2)
22.解下列分式方程:
(1)
(2)
23.如图,点在一条直线上,且,若,.求证:.
24.2019年底在人类社会中传播一种新型病毒一新型冠状病毒,此病毒传染性较强,但经过医学专家、医护人员及全国人民的共同努力,2020年4月新冠肺炎病毒得到有效控制.某学校为迎接学生返校上课,购买了一批口罩,其中购买工厂口罩花费了元,购买工厂口罩花费了元,工厂口罩的每盒单价是工厂口罩每盒单价的倍,购买工厂口罩的数量比购买工厂口罩数量多盒.求:和两工厂口罩的每盒单价分别为多少元? (单位:盒)
25.如图,在中, ,点在边上运动(点不与点重合),连接作交边于点.
(1)当时,_ _, _
(2)当等于多少时,,请说明理由;
26.在社会主义新农村建设中,某乡镇决定对一段公路进行改造,已知这项工程由甲工程队单独做需要40天完成;如果由乙工程先单独做10天,那么剩下的工程还需要两队合做20天才能完成.
(1)求乙工程队单独完成这项工程所需的天数;
(2)求两队合作完成这项工程所需的天数.
参考答案
1.C
【分析】
分式的值为0:分子为0,分母不为0.
【详解】
根据题意,得,
,即,
解得x=3.
故选C.
【点睛】
本题考查了分式的值为零的条件:(1)分子为0;(2)分母不为0.这两个条件缺一不可.
2.C
【分析】
根据全等图形的定义逐项判断即得答案.
【详解】
解:A、不是全等图形,故本选项不符合题意;
B、不是全等图形,故本选项不符合题意;
C、是全等图形,故本选项符合题意;
D、不是全等图形,故本选项不符合题意;
故选:C.
【点睛】
本题考查了全等图形的定义,属于应知应会题型,掌握概念是关键.
3.B
【分析】
将原式中的x、y分别用3x、3y代替,化简,再与原分式进行比较.
【详解】
解:∵把分式中的x与y同时扩大为原来的3倍,
∴原式变为:= =9×,
∴这个分式的值扩大9倍.
故选:B.
【点睛】
本题考查了分式的基本性质.解题的关键是抓住分子、分母变化的倍数,解此类题首先把字母变化后的值代入式子中,然后约分,再与原式比较,最终得出结论.
4.C
【分析】
分别写出四个命题的逆命题,然后分别根据对顶角的定义、等式的性质和平行线的判定进行判断.
【详解】
解:A、如果a=b,那么a2=b2的逆命题是如果a2=b2,那么a=b,也可能是a=﹣b,故逆命题是假命题;
B、若两个数相等,则这两个数的绝对值也相等的逆命题是若这两个数的绝对值相等,则两个数相等,也可能是相反数,故逆命题是假命题;
C、两直线平行,同位角相等的逆命题是同位角相等,两直线平行,逆命题是真命题;
D、对顶角相等的逆命题是相等的角是对顶角,不一定是对顶角,逆命题是假命题;
故选:C.
【点睛】
本题考查了互逆命题,如果一个命题的题设和结论分别是另一个命题的结论和题设,那么这两个命题叫做互逆命题,其中一个命题叫做另一个命题的逆命题.
5.D
【分析】
把除号变成乘号,在进行分式约分即可;
【详解】
.
故选D.
【点睛】
本题主要考查了分式乘除运算,准确计算是解题的关键 .
6.B
【分析】
由≌,得到 再利用线段的和差可得答案
【详解】
解: ≌,
.
,
故选B.
【点睛】
本题考查的是全等三角形的性质,掌握全等三角形的对应边相等是解题的关键.
7.A
【分析】
先通分,然后合并,即可得到答案.
【详解】
解:原式.
【点睛】
本题考查了分式的化简求值,解题的关键是熟练掌握运算法则进行解题.
8.D
【分析】
根据全等三角形的各个判定定理逐一判断即可.
【详解】
解:∵,BC=CB,
若添加,不能证明,故A不符合题意;
若添加,不能证明,故B不符合题意;
若添加,不能证明,故C不符合题意;
若添加,利用SAS即可证明,故D符合题意;
故选D.
【点睛】
此题考查的是使两个三角形全等所需添加的条件,掌握全等三角形的各个判定定理是解决此题的关键.
9.C
【分析】
给括号里分别添加“+、﹣、×、÷”计算,即可得出结论.
【详解】
;
;
;
.
故选C.
【点睛】
本题考查了分式的加减乘除,熟练掌握分式的加减乘除的运算法则是解答的关键.
10.D
【分析】
根据全等三角形的判定方法进行判断即可;
【详解】
乙中根据SAS即可证明全等;
丙中根据AAS即可证明全等;
故选:D.
【点睛】
本题主要考查了全等三角形的判定,准确理解是解题的关键.
11.A
【分析】
根据分式方程的增根的定义得出x-3=0,得到x=3,然后代入化为整式方程的方程算出a的值即可.
【详解】
方程两边都乘x-3得:(x-4)-3(x-3)=a,即a=-2x+5,
∵分式方程有增根,
∴x-3=0,
解得:x=3,
∴a=-2×3+5=-1,
故选:A.
【点睛】
本题考查了分式方程的增根.增根问题可按如下步骤进行:①让最简公分母为0确定增根;②化分式方程为整式方程;③把增根代入整式方程即可求得相关字母的值.
12.A
【分析】
根据全等三角形的基本性质求解即可.
【详解】
已知这两个三角形全等,则三组对应边应分别为2、5、6,所以x=6,y=5,则
x+y=6+5=11,故本题正确答案为A.
【点睛】
本题主要考查全等三角形的基本性质,掌握全等三角形的基本性质是解决本题的关键.
13.D
【分析】
将代入方程得到有关的方程求得的值即可.
【详解】
是分式方程的解,
,
解得,
经检验,是的解,
故选:D.
【点睛】
本题考查了分式方程的解及解分式方程,解题的关键是能正确的根据方程的解的定义代入并得到有关的方程.
14.A
【分析】
根据作图可得DO=D′O′,CO=C′O′,CD=C′D′,再利用SSS判定△D′O′C′≌△DOC即可得出∠O'=∠O.由此即可解决问题.
【详解】
解:由题可得,DO=D′O′,CO=C′O′,CD=C′D′,
∵在△COD和△C′O′D′中,
,
∴△D′O′C′≌△DOC(SSS),
∴∠A'O'B'=∠AOB(全等三角形的对应角相等).
故选:A.
【点睛】
此题主要考查了基本作图,解决问题的关键是掌握作一个角等于已知角的方法,掌握三角形全等的判定方法.
15.A
【分析】
根据方程的等量关系为:骑自行车的时间-乘汽车的时间=h,再根据时间=路程÷速度可知被墨水污损部分的内容.
【详解】
解:由方程可知汽车速度是自行车速度的3倍,结果同时到达.
故选:A
【点睛】
本题考查根据分式方程找已知条件的能力以及路程问题,有一定的难度,解题关键是找准等量关系:骑自行车的时间-乘汽车的时间=h
16.D
【分析】
①根据角平分线的性质与平角的性质即可判断;②易证证,即可判断;③证明即可判断;④过点作于点,于点,得到,故可判断.
【详解】
,分别为,的平分线,,
,故①对.
,,
∴∠F=∠BAP
∴,
,故②对.
由②可知,,,故③对.
过点作于点,于点,
又,,点在的平分线上,故④对
故选D.
【点睛】
此题主要考查全等三角形的判定与性质,解题的关键是熟知角平分线的性质及全等三角形的判定.
17.2.4.
【分析】
根据题意列出分式方程,求出解即可得到x的值.
【详解】
解:根据题意得: ,
去分母得:2﹣3x+10﹣2x=0,
解得:x=2.4,
经检验x=2.4是分式方程的解,
故答案为:2.4.
【点睛】
本题考查的知识点是解分式方程,掌握解分式方程的一般步骤是解此题的关键,注意验根.
18.80
【分析】
设甲车的速度为,则乙车的速度为,根据乙车比甲车早30分钟到达B地列方程求解即可.
【详解】
设甲车的速度为,则乙车的速度为,
依题意,得,
解得:,
经检验,是原方程的解,且符合题意,
故答案为80.
【点睛】
本题考查了分式方程的应用,弄清题意,找准等量关系列出方程是解题的关键.注意分式方程要验根.
19.①③④
【分析】
利用AAS可证明△ABE≌△ACF,可得AC=AB,∠BAE=∠CAF,利用角的和差关系可得∠EAM=∠FAN,可得③正确,利用ASA可证明△AEM≌△AFN,可得EM=FN,AM=AN,可得①③正确;根据线段的和差关系可得CM=BN,利用AAS可证明△CDM≌△BDN,可得CD=DB,可得②错误;利用ASA可证明△ACN≌△ABM,可得④正确;综上即可得答案.
【详解】
在△ABE和△ACF中,,
∴△ABE≌△ACF,
∴AB=AC,∠BAE=∠CAF,
∴∠BAE-∠BAC=∠CAF-∠BAC,即∠FAN=∠EAM,故③正确,
在△AEM和△AFN中,,
∴△AEM≌△AFN,
∴EM=FN,AM=AN,故①正确,
∴AC-AM=AB-AN,即CM=BN,
在△CDM和△BDN中,,
∴CD=DB,故②错误,
在△CAN和△ABM中,,
∴△ACN≌△ABM,故④正确,
综上所述:正确的结论有①③④,
故答案为:①③④
【点睛】
本题考查全等三角形的判定与性质,判定两个三角形全等的方法有:SSS、SAS、AAS、ASA、HL,注意:SSA、AAA不能判定三角形确定,当利用SAS证明时,角必须是两边的夹角;熟练掌握全等三角形的判定定理是解题关键.
20.见解析.
【分析】
利用基本作图来解,作∠B=∠α,∠C=β,BC=2即可.
【详解】
解:如图,为所作.
【点睛】
本题考查尺规作图问题,掌握尺规作图中的基本作图,会用基本作图解决问题是解题关键.
21.(1);(2)
【分析】
(1)先把除法转化为乘法,然后约分化为最简分式即可,
(2)先把括号内分式通分合并,同时将除法化为乘法,利用乘法公式将分子与分母因式分解,然后约分化为最间分式即可.
【详解】
解:,
,
,
,
,
,
,
=.
【点睛】
本题考查分式的加减乘除混合运算,掌握分式的混合运算法则,会按混合运算法则进行加减乘除混合运算,会用乘法公式将分式的分子分母进行因式分解,会通分与约分,分式运算的结果是最简分式.
22.(1)x=5; (2)原分式方程无解.
【分析】
(1)先将方程两边都乘以最简公分母,化分式方程为整式方程,解整式方程求出未知数的值,再检验,从而得出答案;
(2)先将方程两边都乘以最简公分母x﹣4,化分式方程为整式方程,解整式方程求出未知数的值,再检验,从而得出答案.
【详解】
解:(1)方程两边都乘以去分母,得:
去括号,得:
解得:
检验:当时,,
是原方程的解.
两边都乘以,去分母得:
解得
检验:当时,,
是分式方程的增根,
原分式方程无解.
【点睛】
本题主要考查解分式方程,解分式方程的步骤:①去分母;②求出整式方程的解;③检验;④得出结论,会用分式方程的解法解方程是解题关键.
23.证明见解析.
【分析】
由∠1=∠2,根据补角的性质可求出,根据AB=CD可得,根据推出,根据全等三角形的性质即可得出答案.
【详解】
∵,.
又∵,
∴,
∵,
∴,
即,
在 和中,
∴,
∴.
【点睛】
本题考查了全等三角形的性质和判定,能证明是解此题的关键.
24.A工厂口罩的单价为54元每盒,B工厂口罩的单价为45元每盒.
【分析】
设B工厂口罩单价为x元,则A工厂口罩的单价为1.2x元,根据购买工厂口罩花费了元,购买工厂口罩花费了元,购买工厂口罩的数量比购买工厂口罩数量多盒列出方程,解方程即可得解.
【详解】
解:设B工厂口罩单价为x元,则A工厂口罩的单价为1.2x元,
依题意,得:,
解得:x=45,
经检验,x=45是所列分式方程的解,且符合题意,
∴1.2x=54.
答:A工厂口罩的单价为54元每盒,B工厂口罩的单价为45元每盒.
【点睛】
此题考查了分式方程的应用,找出题目蕴含的等量关系是解决问题的关键.
25.(1);(2)当时,理由见解析.
【分析】
(1)利用平角定义,与三角形内角和即可求出两个角,
(2)由一线三等角可推出连个三角形有两组对应角相等,缺少边,为此只要满足DC=AB=3即可.
【详解】
(1)∵,,
∴由平角定义∠EDC=180?--=30?,
∵,
∴,
(2)当时,,
理由如下:
,
,
,
,
,
,
在和中
,
.
【点睛】
本题考查求角的大小与三角形全等问题,涉及平角定义,三角形内角和,一线三等角,三角形全等等知识,掌握并会利用平角定义即求角,会用三角形内角和计算,会利用一线三等角导出角等关系,会根据全等条件确定线段的大小是解题关键.
26.(1)60 (2)24
【分析】
本题主要考查分式方程的应用. 等量关系为:工作时间=工作总量÷工作效率,根据题意可得出:甲队的总工作量+乙队的总工作量=1,由此可列出方程求解.
【详解】
解:(1)设乙工程队单独完成这项工程需要x天,
根据题意得:
解之得:x=60,
经检验:x=60是原方程的解.
所以乙工程队单独完成这项工程所需的天数为60天.
(2)设两队合做完成这项工程所需的天数为y天,
根据题意得:()y=1,
解之得:y=24,
所以两队合做完成这项工程所需的天数为24天.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若分式的值为0,则x的值是( )
A.±3 B.﹣3 C.3 D.0
2.如图所示的图形是全等图形的是( )
A. B. C. D.
3.将分式中的x,y的值同时扩大为原来的3倍,则分式的值( )
A.扩大6倍 B.扩大9倍 C.不变 D.扩大3倍
4.下列命题的逆命题是真命题的是( )
A.如果a=b,那么a2=b2
B.若两个数相等,则这两个数的绝对值也相等
C.两直线平行,同位角相等
D.对顶角相等
5.计算的结果是( )
A.1 B. C. D.
6.如图,≌,,,则的长为( )
A.2 B.3 C.5 D.7
7.化简的结果是( )
A. B. C. D.
8.如图,已知,要使,只需要添加一个条件是( )
A. B. C. D.
9.若分式运算的结果为x,则在□中添加的运算符号为( )
A.+ B.-或÷ C.-或÷ D.+或×
10.下列各图中,为三角形的边长,则甲,乙、丙三个三角形和左侧全等的是( )
A.甲和乙 B.只有乙 C.甲和丙 D.乙和丙
11.若关于x的分式方程有增根,则的值是( )
A. B. C.3 D.
12.一个三角形的三边长分别为2,5,x,另一个三角形的三边长分别为y,2,6,若这两个三角形全等,则x+y=( )
A.11 B.7 C.8 D.13
13.是分式方程的解,则a的值是( )
A. B.0 C.1 D.3
14.下面“作一个角等于已知角”的尺规作图过程.已知:,求作:一个角,使它等于.作法:如图
(1)作射线;
(2)以为圆心﹐任意长为半径作孤,交于,交于;
(3)以为圆心,为半径作弧,交于;
(4)以为圆心,为半径作弧﹐交弧于;
(5)过点作射线.
则就是所求作的角.
请回答:该作图的依据是( )
A. B. C. D.
15.某班学生到距学校12km的烈士陵园扫墓,一部分同学骑自行车先行,经h后,其余同学乘汽车出发,由于□□□□□□,设自行车的速度为xkm/h,则可得方程为,根据此情境和所列方程,上题中□□□□□□表示被墨水污损部分的内容,其内容应该是( )
A.汽车速度是自行车速度的3倍,结果同时到达
B.汽车速度是自行车速度的3倍,后部分同学比前部分同学迟到h
C.汽车速度是自行车速度的3倍,前部分同学比后部分同学迟到h
D.汽车速度比自行车速度每小时多3km,结果同时到达
16.如图,在中,,的角平分线,相交于点,过点作交的延长线于点,交于点.则下列结论:①;②;③;④连接,平分.其中正确的是( ).
A.①②③ B.①②④ C.①③④ D.①②③④
二、填空题
17.当x=_____时,分式与分式的值互为相反数.
18.甲、乙两辆汽车同时从地出发,开往相距的地,甲、乙两车的速度之比是,结果乙车比甲车早分钟到达地,则甲车的速度为_____.
19.如图,给出下列结论:①;②;③;④.其中正确的有_______(填写答案序号).
三、解答题
20.尺规作图:已知和线段,求作,使.(作图痕迹要清晰规范,不要求作图步骤)
21.计算下列各式:
(1)
(2)
22.解下列分式方程:
(1)
(2)
23.如图,点在一条直线上,且,若,.求证:.
24.2019年底在人类社会中传播一种新型病毒一新型冠状病毒,此病毒传染性较强,但经过医学专家、医护人员及全国人民的共同努力,2020年4月新冠肺炎病毒得到有效控制.某学校为迎接学生返校上课,购买了一批口罩,其中购买工厂口罩花费了元,购买工厂口罩花费了元,工厂口罩的每盒单价是工厂口罩每盒单价的倍,购买工厂口罩的数量比购买工厂口罩数量多盒.求:和两工厂口罩的每盒单价分别为多少元? (单位:盒)
25.如图,在中, ,点在边上运动(点不与点重合),连接作交边于点.
(1)当时,_ _, _
(2)当等于多少时,,请说明理由;
26.在社会主义新农村建设中,某乡镇决定对一段公路进行改造,已知这项工程由甲工程队单独做需要40天完成;如果由乙工程先单独做10天,那么剩下的工程还需要两队合做20天才能完成.
(1)求乙工程队单独完成这项工程所需的天数;
(2)求两队合作完成这项工程所需的天数.
参考答案
1.C
【分析】
分式的值为0:分子为0,分母不为0.
【详解】
根据题意,得,
,即,
解得x=3.
故选C.
【点睛】
本题考查了分式的值为零的条件:(1)分子为0;(2)分母不为0.这两个条件缺一不可.
2.C
【分析】
根据全等图形的定义逐项判断即得答案.
【详解】
解:A、不是全等图形,故本选项不符合题意;
B、不是全等图形,故本选项不符合题意;
C、是全等图形,故本选项符合题意;
D、不是全等图形,故本选项不符合题意;
故选:C.
【点睛】
本题考查了全等图形的定义,属于应知应会题型,掌握概念是关键.
3.B
【分析】
将原式中的x、y分别用3x、3y代替,化简,再与原分式进行比较.
【详解】
解:∵把分式中的x与y同时扩大为原来的3倍,
∴原式变为:= =9×,
∴这个分式的值扩大9倍.
故选:B.
【点睛】
本题考查了分式的基本性质.解题的关键是抓住分子、分母变化的倍数,解此类题首先把字母变化后的值代入式子中,然后约分,再与原式比较,最终得出结论.
4.C
【分析】
分别写出四个命题的逆命题,然后分别根据对顶角的定义、等式的性质和平行线的判定进行判断.
【详解】
解:A、如果a=b,那么a2=b2的逆命题是如果a2=b2,那么a=b,也可能是a=﹣b,故逆命题是假命题;
B、若两个数相等,则这两个数的绝对值也相等的逆命题是若这两个数的绝对值相等,则两个数相等,也可能是相反数,故逆命题是假命题;
C、两直线平行,同位角相等的逆命题是同位角相等,两直线平行,逆命题是真命题;
D、对顶角相等的逆命题是相等的角是对顶角,不一定是对顶角,逆命题是假命题;
故选:C.
【点睛】
本题考查了互逆命题,如果一个命题的题设和结论分别是另一个命题的结论和题设,那么这两个命题叫做互逆命题,其中一个命题叫做另一个命题的逆命题.
5.D
【分析】
把除号变成乘号,在进行分式约分即可;
【详解】
.
故选D.
【点睛】
本题主要考查了分式乘除运算,准确计算是解题的关键 .
6.B
【分析】
由≌,得到 再利用线段的和差可得答案
【详解】
解: ≌,
.
,
故选B.
【点睛】
本题考查的是全等三角形的性质,掌握全等三角形的对应边相等是解题的关键.
7.A
【分析】
先通分,然后合并,即可得到答案.
【详解】
解:原式.
【点睛】
本题考查了分式的化简求值,解题的关键是熟练掌握运算法则进行解题.
8.D
【分析】
根据全等三角形的各个判定定理逐一判断即可.
【详解】
解:∵,BC=CB,
若添加,不能证明,故A不符合题意;
若添加,不能证明,故B不符合题意;
若添加,不能证明,故C不符合题意;
若添加,利用SAS即可证明,故D符合题意;
故选D.
【点睛】
此题考查的是使两个三角形全等所需添加的条件,掌握全等三角形的各个判定定理是解决此题的关键.
9.C
【分析】
给括号里分别添加“+、﹣、×、÷”计算,即可得出结论.
【详解】
;
;
;
.
故选C.
【点睛】
本题考查了分式的加减乘除,熟练掌握分式的加减乘除的运算法则是解答的关键.
10.D
【分析】
根据全等三角形的判定方法进行判断即可;
【详解】
乙中根据SAS即可证明全等;
丙中根据AAS即可证明全等;
故选:D.
【点睛】
本题主要考查了全等三角形的判定,准确理解是解题的关键.
11.A
【分析】
根据分式方程的增根的定义得出x-3=0,得到x=3,然后代入化为整式方程的方程算出a的值即可.
【详解】
方程两边都乘x-3得:(x-4)-3(x-3)=a,即a=-2x+5,
∵分式方程有增根,
∴x-3=0,
解得:x=3,
∴a=-2×3+5=-1,
故选:A.
【点睛】
本题考查了分式方程的增根.增根问题可按如下步骤进行:①让最简公分母为0确定增根;②化分式方程为整式方程;③把增根代入整式方程即可求得相关字母的值.
12.A
【分析】
根据全等三角形的基本性质求解即可.
【详解】
已知这两个三角形全等,则三组对应边应分别为2、5、6,所以x=6,y=5,则
x+y=6+5=11,故本题正确答案为A.
【点睛】
本题主要考查全等三角形的基本性质,掌握全等三角形的基本性质是解决本题的关键.
13.D
【分析】
将代入方程得到有关的方程求得的值即可.
【详解】
是分式方程的解,
,
解得,
经检验,是的解,
故选:D.
【点睛】
本题考查了分式方程的解及解分式方程,解题的关键是能正确的根据方程的解的定义代入并得到有关的方程.
14.A
【分析】
根据作图可得DO=D′O′,CO=C′O′,CD=C′D′,再利用SSS判定△D′O′C′≌△DOC即可得出∠O'=∠O.由此即可解决问题.
【详解】
解:由题可得,DO=D′O′,CO=C′O′,CD=C′D′,
∵在△COD和△C′O′D′中,
,
∴△D′O′C′≌△DOC(SSS),
∴∠A'O'B'=∠AOB(全等三角形的对应角相等).
故选:A.
【点睛】
此题主要考查了基本作图,解决问题的关键是掌握作一个角等于已知角的方法,掌握三角形全等的判定方法.
15.A
【分析】
根据方程的等量关系为:骑自行车的时间-乘汽车的时间=h,再根据时间=路程÷速度可知被墨水污损部分的内容.
【详解】
解:由方程可知汽车速度是自行车速度的3倍,结果同时到达.
故选:A
【点睛】
本题考查根据分式方程找已知条件的能力以及路程问题,有一定的难度,解题关键是找准等量关系:骑自行车的时间-乘汽车的时间=h
16.D
【分析】
①根据角平分线的性质与平角的性质即可判断;②易证证,即可判断;③证明即可判断;④过点作于点,于点,得到,故可判断.
【详解】
,分别为,的平分线,,
,故①对.
,,
∴∠F=∠BAP
∴,
,故②对.
由②可知,,,故③对.
过点作于点,于点,
又,,点在的平分线上,故④对
故选D.
【点睛】
此题主要考查全等三角形的判定与性质,解题的关键是熟知角平分线的性质及全等三角形的判定.
17.2.4.
【分析】
根据题意列出分式方程,求出解即可得到x的值.
【详解】
解:根据题意得: ,
去分母得:2﹣3x+10﹣2x=0,
解得:x=2.4,
经检验x=2.4是分式方程的解,
故答案为:2.4.
【点睛】
本题考查的知识点是解分式方程,掌握解分式方程的一般步骤是解此题的关键,注意验根.
18.80
【分析】
设甲车的速度为,则乙车的速度为,根据乙车比甲车早30分钟到达B地列方程求解即可.
【详解】
设甲车的速度为,则乙车的速度为,
依题意,得,
解得:,
经检验,是原方程的解,且符合题意,
故答案为80.
【点睛】
本题考查了分式方程的应用,弄清题意,找准等量关系列出方程是解题的关键.注意分式方程要验根.
19.①③④
【分析】
利用AAS可证明△ABE≌△ACF,可得AC=AB,∠BAE=∠CAF,利用角的和差关系可得∠EAM=∠FAN,可得③正确,利用ASA可证明△AEM≌△AFN,可得EM=FN,AM=AN,可得①③正确;根据线段的和差关系可得CM=BN,利用AAS可证明△CDM≌△BDN,可得CD=DB,可得②错误;利用ASA可证明△ACN≌△ABM,可得④正确;综上即可得答案.
【详解】
在△ABE和△ACF中,,
∴△ABE≌△ACF,
∴AB=AC,∠BAE=∠CAF,
∴∠BAE-∠BAC=∠CAF-∠BAC,即∠FAN=∠EAM,故③正确,
在△AEM和△AFN中,,
∴△AEM≌△AFN,
∴EM=FN,AM=AN,故①正确,
∴AC-AM=AB-AN,即CM=BN,
在△CDM和△BDN中,,
∴CD=DB,故②错误,
在△CAN和△ABM中,,
∴△ACN≌△ABM,故④正确,
综上所述:正确的结论有①③④,
故答案为:①③④
【点睛】
本题考查全等三角形的判定与性质,判定两个三角形全等的方法有:SSS、SAS、AAS、ASA、HL,注意:SSA、AAA不能判定三角形确定,当利用SAS证明时,角必须是两边的夹角;熟练掌握全等三角形的判定定理是解题关键.
20.见解析.
【分析】
利用基本作图来解,作∠B=∠α,∠C=β,BC=2即可.
【详解】
解:如图,为所作.
【点睛】
本题考查尺规作图问题,掌握尺规作图中的基本作图,会用基本作图解决问题是解题关键.
21.(1);(2)
【分析】
(1)先把除法转化为乘法,然后约分化为最简分式即可,
(2)先把括号内分式通分合并,同时将除法化为乘法,利用乘法公式将分子与分母因式分解,然后约分化为最间分式即可.
【详解】
解:,
,
,
,
,
,
,
=.
【点睛】
本题考查分式的加减乘除混合运算,掌握分式的混合运算法则,会按混合运算法则进行加减乘除混合运算,会用乘法公式将分式的分子分母进行因式分解,会通分与约分,分式运算的结果是最简分式.
22.(1)x=5; (2)原分式方程无解.
【分析】
(1)先将方程两边都乘以最简公分母,化分式方程为整式方程,解整式方程求出未知数的值,再检验,从而得出答案;
(2)先将方程两边都乘以最简公分母x﹣4,化分式方程为整式方程,解整式方程求出未知数的值,再检验,从而得出答案.
【详解】
解:(1)方程两边都乘以去分母,得:
去括号,得:
解得:
检验:当时,,
是原方程的解.
两边都乘以,去分母得:
解得
检验:当时,,
是分式方程的增根,
原分式方程无解.
【点睛】
本题主要考查解分式方程,解分式方程的步骤:①去分母;②求出整式方程的解;③检验;④得出结论,会用分式方程的解法解方程是解题关键.
23.证明见解析.
【分析】
由∠1=∠2,根据补角的性质可求出,根据AB=CD可得,根据推出,根据全等三角形的性质即可得出答案.
【详解】
∵,.
又∵,
∴,
∵,
∴,
即,
在 和中,
∴,
∴.
【点睛】
本题考查了全等三角形的性质和判定,能证明是解此题的关键.
24.A工厂口罩的单价为54元每盒,B工厂口罩的单价为45元每盒.
【分析】
设B工厂口罩单价为x元,则A工厂口罩的单价为1.2x元,根据购买工厂口罩花费了元,购买工厂口罩花费了元,购买工厂口罩的数量比购买工厂口罩数量多盒列出方程,解方程即可得解.
【详解】
解:设B工厂口罩单价为x元,则A工厂口罩的单价为1.2x元,
依题意,得:,
解得:x=45,
经检验,x=45是所列分式方程的解,且符合题意,
∴1.2x=54.
答:A工厂口罩的单价为54元每盒,B工厂口罩的单价为45元每盒.
【点睛】
此题考查了分式方程的应用,找出题目蕴含的等量关系是解决问题的关键.
25.(1);(2)当时,理由见解析.
【分析】
(1)利用平角定义,与三角形内角和即可求出两个角,
(2)由一线三等角可推出连个三角形有两组对应角相等,缺少边,为此只要满足DC=AB=3即可.
【详解】
(1)∵,,
∴由平角定义∠EDC=180?--=30?,
∵,
∴,
(2)当时,,
理由如下:
,
,
,
,
,
,
在和中
,
.
【点睛】
本题考查求角的大小与三角形全等问题,涉及平角定义,三角形内角和,一线三等角,三角形全等等知识,掌握并会利用平角定义即求角,会用三角形内角和计算,会利用一线三等角导出角等关系,会根据全等条件确定线段的大小是解题关键.
26.(1)60 (2)24
【分析】
本题主要考查分式方程的应用. 等量关系为:工作时间=工作总量÷工作效率,根据题意可得出:甲队的总工作量+乙队的总工作量=1,由此可列出方程求解.
【详解】
解:(1)设乙工程队单独完成这项工程需要x天,
根据题意得:
解之得:x=60,
经检验:x=60是原方程的解.
所以乙工程队单独完成这项工程所需的天数为60天.
(2)设两队合做完成这项工程所需的天数为y天,
根据题意得:()y=1,
解之得:y=24,
所以两队合做完成这项工程所需的天数为24天.
同课章节目录
