河北省临西县2020-2021学年八年级上学期期中数学试题(word版,含答案)
文档属性
| 名称 | 河北省临西县2020-2021学年八年级上学期期中数学试题(word版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 780.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 16:36:30 | ||
图片预览




文档简介
河北省临西县2020-2021学年八年级上学期期中数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列四个选项中的图形与下面的图形全等的是( )
A. B. C. D.
2.赵师傅在做完门框后,为防止变形,按图中所示的方法在门上钉了两根斜拉的木条(图中的两根木条),其中运用的几何原理是( )
A.两点之间线段最短 B.三角形两边之和大于第三边
C.垂线段最短 D.三角形的稳定性
3.如图,是的中线,若,则的长为( )
A. B. C. D.
4.如图,,且,则的度数为( )
A. B. C. D.
5.如图,六角螺母的横截面是正六边形,则的度数为( )
A.60° B.120° C.45° D.75°
6.如图,用三角板作的边上的高线,下列三角板的摆放位置正确的是( )
A. B. C. D.
7.将一副三角板按图中的方式叠放,则的度数为( )
A. B. C. D.
8.如图,,四个点在同一直线上,若,则的长是 ( )
A.2 B.3 C.5 D.7
9.在下列条件中:
①∠A+∠B=∠C,②∠A:∠B:∠C=1:2:3,③∠A=2∠B=3∠C,④中,能确定△ABC是直角三角形的条件有( )
A.1个 B.2个 C.3个 D.4个
10.若将长度分别为的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折断),则该三角形的最长边的长为( )
A. B. C. D.
11.下面是投影屏上出示的解答题,需要回答横线上符号代表的内容.
如图,直线直线,在中,,顶点在上,顶点在上,且平分,若,求的度数.
解:∵,,
∴_______①_______,
∵直线直线,
∴_____②______,
∵平分,
∴_____③_____= ,
∵直线直线,
∴___④_____= ,
下列选项错误的是( )
A.①代表64° B.②代表 C.③代表 D.④代表
12.如图,在中,,,,那么的度数为( )
A.64° B.54° C.44° D.36°
13.在中, ,若的平分线交于点,则的度数是( )
A. B. C. D.
14.在△ABC中,,则△ABC是( )
A.等腰直角三角形 B.锐角三角形 C.钝角三角形 D.直角三角形
15.对于题目:如图,是的角平分线,于点,若,求的度数.下面是打乱了的解题过程:①∵;②;③∵平分,∴;④∵,,则下列排序正确的是( ).
A.③④②① B.④②①③ C.③②④① D.③①④②
16.如图,中,,且,,则 的度数为( )
A.80° B.60° C.40° D.20°
二、填空题
17.在中,若,,则的度数为_________.
18.三角形的外角和等于_____度.
三、解答题
19.一个机器人以的速度在平地上按如下要求行走,
(1)该机器人从开始到停止所走过的路程形成的图形是_____;
(2)该机器人从开始到停止所需时间为_______;
(3)若机器人还差就第次回到点处,则它所走过的路程为_____.
20.(1)如图1,的外角为116°,,求的余角的度数.
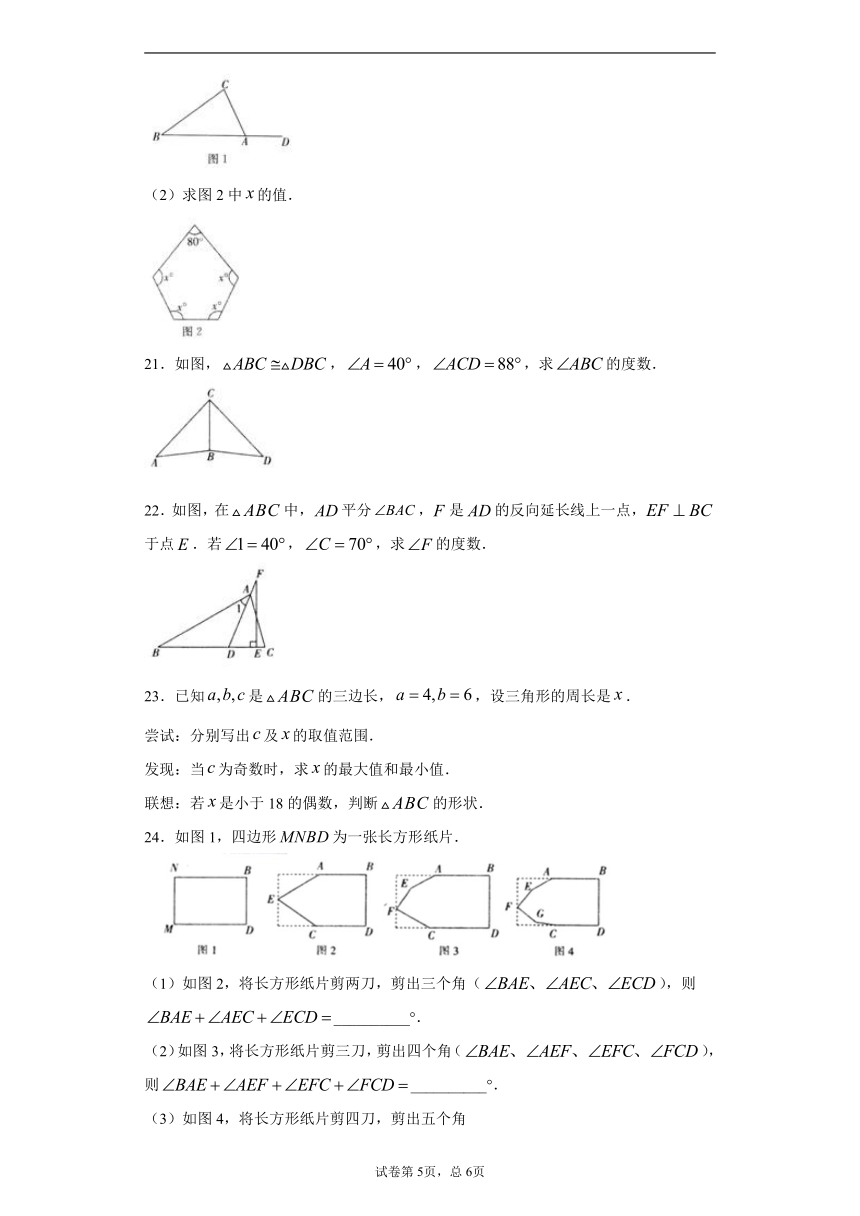
(2)求图2中的值.
21.如图,,,,求的度数.
22.如图,在中,平分,是的反向延长线上一点,于点.若,,求的度数.
23.已知是的三边长,,设三角形的周长是.
尝试:分别写出及的取值范围.
发现:当为奇数时,求的最大值和最小值.
联想:若是小于18的偶数,判断的形状.
24.如图1,四边形为一张长方形纸片.
(1)如图2,将长方形纸片剪两刀,剪出三个角(),则__________°.
(2)如图3,将长方形纸片剪三刀,剪出四个角(),则__________°.
(3)如图4,将长方形纸片剪四刀,剪出五个角(),则___________°.
(4)根据前面探索出的规律,将本题按照上述剪法剪刀,剪出个角,那么这个角的和是____________°.
25.如图,,其中点在同一条直线上..
(1)若,,求的大小;
(2)若,,求的长.
26.如图,在四边形 中,和分别平分四边形的外角和,与相交于点,若.
(1)如图1,若,求的度数;
(2)如图1,若,试猜想所满足的数量关系式,并说明理由.
(3)如图2,若,判断的位置关系,并说明理由.
参考答案
1.B
【解析】
分析:根据图形全等的定义解答即可.
详解:能够与已知图形重合的只有.故选B.
点睛:本题考查了全等的定义.掌握图形全等的定义是解答的关键.
2.D
【分析】
三角形具有稳定性,其它多边形不具有稳定性,把多边形分割成三角形则多边形的形状就不会改变.
【详解】
赵师傅这样做是运用了三角形的稳定性.
故选:D.
【点睛】
本题考查了三角形稳定性的实际应用.三角形的稳定性在实际生活中有着广泛的应用,如钢架桥、房屋架梁等,因此要使一些图形具有稳定的结构,往往通过连接辅助线转化为三角形而获得.
3.C
【分析】
根据中线的定义解答即可.
【详解】
由题意知,点D是线段AB的中点,
∵AB=8,
∴AD=AB=4,
故选:C.
【点睛】
本题考查三角形的中线,属于基础题型.
4.B
【分析】
根据全等三角形的性质即可求解.
【详解】
解:∵
∴∠ACB=∠DCE
即∠ACD+∠DCB=∠BCE+∠DCB
∴∠ACD=
故选:B.
【点睛】
此题主要考查全等三角形的性质,灵活运用性质是解题关键.
5.A
【分析】
根据题意可知为正六边形一外角,依据多边形外角和为360°进行分析即可.
【详解】
解:∵多边形外角和为360°,
∴正六边形一外角为:360°6=60°,即=60°
故选:A.
【点睛】
本题考查多边形的外角,熟练掌握多边形外角和为360°以及多边形外角的定义是解题的关键.
6.B
【分析】
从三角形的一个顶点向底边作垂线,垂足与顶点之间的线段叫做三角形的高.根据高线的定义即可得出结论.
【详解】
解:A.作出的是△ABC中BC边上的高线,故本选项错误;
B.作出的是△ABC中AB边上的高线,故本选项正确;
C.不能作出△ABC中AB边上的高线,故本选项错误;
D.作出的是△ABC中AC边上的高线,故本选项错误;
故选:B.
【点睛】
本题考查的是作图-基本作图,熟知三角形高线的定义是解答此题的关键.
7.A
【分析】
如图,根据三角板的特点可得∠2与∠3的度数,然后根据三角形的外角性质即得答案.
【详解】
解:如图,∵∠2=45°,∠3=60°,∴∠1=∠2+∠3=105°.
故选:A.
【点睛】
本题以学生常见的三角板为载体,主要考查了三角形的外角性质,属于应知应会题型,熟练掌握三角形的外角性质是解题关键.
8.B
【分析】
根据全等三角形的对应边相等得到EF=BC=8,计算即可.
【详解】
∵△ABC≌△DEF,
∴BC=EF,
又BC=8,
∴EF=8,
∵EC=5,
∵CF=EF-EC=8-5=3.
故选:B.
【点睛】
本题考查了全等三角形的性质,掌握全等三角形的对应边相等、全等三角形的对应角相等是解题的关键.
9.C
【分析】
根据有一个角是直角的三角形是直角三角形进行逐一判断即可.
【详解】
解:①∠A+∠B=∠C,又由∠A+∠B+∠C=180°,得到∠C=90°,所以△ABC是直角三角形;
②∠A:∠B:∠C=1:2:3,根据∠A+∠B+∠C=180°,可得到∠A=30°,∠B=60°,∠C=90°,所以△ABC是直角三角形;
③∠A=2∠B=3∠C,即∠B=∠A,∠C=∠A,所以∠A+∠A+∠A=180°,得到∠A=,由于∠A为最大角,所以△ABC不是直角三角形;
④,即,,得到,所以,所以△ABC是直角三角形;
正确的有3个,
故选:C.
【点睛】
本题考查了直角三角形的定义,找到△ABC中是否有直角是解题的关键.
10.C
【分析】
利用三角形的三边关系列举出所围成三角形的不同情况,通过比较得到结论.
【详解】
①长度分别为7、4、5,能构成三角形,且最长边为7;
②长度分别为8、4、4,不能构成三角形;
③长度分别为8、5、3,不能构成三角形;
④长度分别为9、4、3,不能构成三角形;
综上所述,得到三角形的最长边长为7.
故选:C.
【点睛】
本题考查了三角形的三边关系,利用了三角形中三边的关系求解.注意分类讨论,不重不漏.
11.D
【分析】
先利用三角形内角和定理求得,再根据平行线的性质求得,最后利用角平分线的定义结合平行线的性质即可求解
【详解】
∵,,
∴64,
∵直线直线,
∴,
∵平分,
∴= ,
∵直线直线,
∴ .
∴①代表64°,②代表,③代表,④应该代表.
故选:D.
【点睛】
本题考查了平行线的性质,角平分线的定义以及三角形内角和定理,利用各角之间的关系,找出是解题的关键.
12.B
【分析】
根据平行线的性质和直角三角形的两锐角互余即可求得∠B的度数.
【详解】
∵CD∥AB,∠ACD=36?,
∴∠A=∠ACD=36?,
∵在△ABC中,∠ACB=90?,
∴∠B=90?-∠ACB=90?-36?=54?,
故选:B.
【点睛】
本题考查了平行线的性质、直角三角形的性质,熟知直角三角形的两锐角互余是解答的关键.
13.B
【分析】
由的度数可以求出与的和,由角平分线的性质可以得出,,即可得出与的和,即可得出的度数.
【详解】
∵,
∴+=110°,
∵为与的平分线,
∴,,
∴+=110÷2=55°,
∴=180°-55°=125°.
故选:B.
【点睛】
本题主要考查角平分线的性质以及三角形的内角和定理,熟记相关概念是解题关键.
14.D
【分析】
根据题意,可设∠A=x,表示出∠B,∠C的度数.根据三角形内角和定理列方程求出各角的度数再判断三角形的形状.
【详解】
解:设∠A=x,∵,
∴∠B=2x,∠C=3x,
根据三角形内角和定理得,x+2x+3x=180,
解得 x=30,
则2x=60,3x=90,
即三角形内角分别为30°,60°,90°,
∴此三角形是直角三角形.
故选D.
【点睛】
此题考查三角形内角和定理及判断三角形的形状,属基础题.
15.A
【分析】
根据角平分线、直角三角形的性质计算,即可得到答案.
【详解】
∵平分
∴
∵
∴
∴
∴
故选:A.
【点睛】
本题考查了角平分线、直角三角形的知识;解题的关键是熟练掌握角平分线、直角三角形两锐角互余的性质,从而完成求解.
16.C
【分析】
连接FB,根据三角形内角和和外角知识,进行角度计算即可.
【详解】
解:如图连接FB,
∵,,
∴,
∴,
即,
又∵,
∴,
∵,
∴,
故选:C.
【点睛】
此题考查三角形内角和和外角定义,掌握三角形内角和为180°,三角形一个外角等于不相邻两内角之和是解题关键.
17.
【分析】
根据直角三角形的性质解答即可.
【详解】
∵在Rt△ABC中,∠C=90°,∠B=35°,
∴∠A=90°-35°=55°,
故答案为:55°.
【点睛】
本题考查了直角三角形的性质,关键是根据直角三角形的两锐角互余.
18.360.
【分析】
根据任何多边形的外角和是360度即可求解.
【详解】
解:三角形的外角和等于360°.
故答案是:360.
【点睛】
本题考查三角形外角和的性质,解题关键是根据任何多边形的外角和是360度即可求解.
19.(1)正八边形;(2);(3)
【分析】
(1)该机器人所经过的路径是一个正多边形,利用360°除以45°,即可求得正多边形的边数;
(2)求出多边形的周长,利用周长除以速度即可求得所需时间
(3)求出n次的路径长减去4即可.
【详解】
解:(1)由题意得,该机器人所经过的路径是一个正多边形,
多边形的边数为:360°÷45°=8,
所以,该机器人从开始到停止所走过的路程形成的图形是正八边形,
故答案为:正八边形;
(2)该机器人所走的路程是:4×8=32(m),
则所用时间是:32÷2=16(s).
故答案是:16;
(3)已知机器人n次回到原点的路程为:n×32=32n,
还差4m,即:(32n-4)m.
故答案为:(32n-4)m.
【点睛】
本题考查了正多边形的外角和定理,理解经过的路线是正多边形是关键.
20.(1);(2).
【分析】
(1)根据三角形的外角性质求出∠B,根据余角的概念计算,得到答案;
(2)先求得五边形的内角和,再列出方程即可求解.
【详解】
(1)∵∠B=∠CAD-∠C=116°-80°=36°,
∴∠B的余角=90°-36°=54°;
(2)∵五边形的内角和为540°,
∴,
解得.
【点睛】
本题考查了三角形的外角性质,多边形的内角和,余角的概念,掌握三角形的一个外角等于和它不相邻的两个内角的和以及多边形内角和公式是解题的关键.
21.
【分析】
根据全等三角形的性质得出∠ACB=∠DCB,求出∠ACB,根据三角形内角和定理求出即可.
【详解】
∵△ABC≌△DBC,
∴∠ACB=∠DCB,
∵∠ACD=88°,
∴∠ACB=44°,
∵∠A=40°,
∴∠ABC=180°-∠A-∠ACB=96°.
【点睛】
本题考查了三角形内角和定理和全等三角形的性质,能熟记全等三角形的性质是解此题的关键,注意:全等三角形的对应角相等.
22.
【分析】
根据角平分线的性质得到,求出,利用及三角形的内角和定理求出,根据三角形的外角性质求出,再根据直角三角形的性质求出答案.
【详解】
解:∵平分,
∴,
∵,
∴,,
∵,
∴,
∴,
∵,
∴在中,.
【点睛】
此题考查角平分线的性质,三角形的内角和定理,直角三角形两锐角互余,理解图形中各角度之间的关系是解题的关键.
23.尝试:,;发现:的最大值为,的最小值为;联想:是等腰三角形.
【分析】
尝试:根据三角形三边关系即可得出及的取值范围;
发现:由a、b为偶数,c是奇数可得x也为奇数,利用x的取值范围可知其最大值和最小值;
联想:由x是小于18的偶数和取值范围即可作出判断.
【详解】
解:尝试:∵,
∴,
∴周长的取值范围为;
发现:∵,且为奇数,
∴也为奇数,
∵的范围为,
∴的最大值为19,最小值为13;
联想:∵周长为小于18的偶数,且取值范围为,
∴或,
当为16时,,
当为14时,,
当时,,为等腰三角形;
当时,,为等腰三角形,
综上所述,是等腰三角形.
【点睛】
本题考查了三角形的三边关系、不等式的整数解、等腰三角形的判定,利用三边关系得出第三边的取值范围是解答的关键.
24.(1)360;(2)540;(3)720;(4).
【分析】
(1)过点E作EH∥AB,再根据两直线平行,同旁内角互补即可得到三个角的和等于180°的2倍;
(2)分别过E、F分别作AB的平行线,根据两直线平行,同旁内角互补即可得到四个角的和等于180°的三倍;
(3)分别过E、F、G分别作AB的平行线,根据两直线平行,同旁内角互补即可得到四个角的和等于180°的三倍;
(4)根据前三问个的剪法,剪n刀,剪出n+1个角,那么这n+1个角的和是180n度.
【详解】
(1)过E作EH∥AB(如图②).
∵原四边形是长方形,
∴AB∥CD,
又∵EH∥AB,
∴CD∥EH(平行于同一条直线的两条直线互相平行).
∵EH∥AB,
∴∠A+∠1=180°(两直线平行,同旁内角互补).
∵CD∥EH,
∴∠2+∠C=180°(两直线平行,同旁内角互补).
∴∠A+∠1+∠2+∠C=360°,
又∵∠1+∠2=∠AEC,
∴∠BAE+∠AEC+∠ECD=360°;
(2)分别过E、F分别作AB的平行线,如图③所示,
用上面的方法可得∠BAE+∠AEF+∠EFC+∠FCD=540°;
(3)分别过E、F、G分别作AB的平行线,如图④所示,
用上面的方法可得∠BAE+∠AEF+∠EFG+∠FGC+∠GCD=720°;
(4)由此可得一般规律:剪n刀,剪出n+1个角,那么这n+1个角的和是180n度.
故答案为:(1)360;(2)540;(3)720;(4)180n.
【点睛】
本题主要考查了多边形的内角和,作平行线并利用两直线平行,同旁内角互补是解本题的关键,总结规律求解是本题的难点.
25.(1);(2)3cm.
【分析】
(1)根据垂直的定义及全等三角形的性质得到,即可求出的大小;
(2)利用推出AB=CD,再根据已知得出,即可求出答案.
【详解】
解:(1)∵,
∴,
∵,
∴,
∴.
(2)∵,
∴,
∴,即.
∵,,
∴,
∴.
【点睛】
此题考查三角形全等的性质,垂直的定义,正确理解图形中的对应关系是解题的关键.
26.(1);(2);(3),理由见解析.
【分析】
(1)利用角平分线的定义和四边形的内角和以及α+β=168°推导即可;
(2)利用角平分线的定义和四边形的内角和以及三角形的内角和转化即可;
(3)利用角平分线的定义和四边形的内角和以及三角形的外角的性质计算即可.
【详解】
(1)在四边形ABCD中,∠BAD+∠ABC+∠BCD+∠ADC=360°,
∴∠ABC+∠ADC=360°-(α+β),
∵∠MBC+∠ABC=180°,∠NDC+∠ADC=180°
∴∠MBC+∠NDC=180°-∠ABC+180°-∠ADC=360°-(∠ABC+∠ADC)
=360°-[360°-(α+β)]=α+β,
∵α+β=168°,
∴∠MBC+∠NDC=168°;
(2)β-α=70°
理由:如图1,连接BD,
由(1)有,∠MBC+∠NDC=α+β,
∵BE、DF分别平分四边形的外角∠MBC和∠NDC,
∴∠CBG=∠MBC,∠CDG=∠NDC,
∴∠CBG+∠CDG=∠MBC+∠NDC=(∠MBC+∠NDC)=(α+β),
在△BCD中,∠BDC+∠DBC=180°-∠BCD=180°-β,
在△BDG中,∠BGD=35°,
∴∠GBD+∠GDB+∠BGD=180°,
∴∠CBG+∠CBD+∠CDG+∠BDC+∠BGD=180°,
∴(∠CBG+∠CDG)+(∠BDC+∠CDB)+∠BGD=180°,
∴(α+β)+180°-β+35°=180°,
∴β-α=70°;
(3)平行,
理由:如图2,延长BC交DF于H,
由(1)有,∠MBC+∠NDC=α+β,
∵BE、DF分别平分四边形的外角∠MBC和∠NDC,
∴∠CBE=∠MBC,∠CDH=∠NDC,
∴∠CBE+∠CDH=∠MBC+∠NDC=(∠MBC+∠NDC)=(α+β),
∵∠BCD=∠CDH+∠DHB,
∴∠CDH=∠BCD-∠DHB=β-∠DHB,
∴∠CBE+β-∠DHB=(α+β),
∵α=β,
∴∠CBE+β-∠DHB=(β+β)=β,
∴∠CBE=∠DHB,
∴BE∥DF.
【点睛】
本题主要考查了平角的意义,四边形的内角和,三角形内角和,三角形的外角性质,角平分线的意义,用整体代换的思想是解本题的关键.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列四个选项中的图形与下面的图形全等的是( )
A. B. C. D.
2.赵师傅在做完门框后,为防止变形,按图中所示的方法在门上钉了两根斜拉的木条(图中的两根木条),其中运用的几何原理是( )
A.两点之间线段最短 B.三角形两边之和大于第三边
C.垂线段最短 D.三角形的稳定性
3.如图,是的中线,若,则的长为( )
A. B. C. D.
4.如图,,且,则的度数为( )
A. B. C. D.
5.如图,六角螺母的横截面是正六边形,则的度数为( )
A.60° B.120° C.45° D.75°
6.如图,用三角板作的边上的高线,下列三角板的摆放位置正确的是( )
A. B. C. D.
7.将一副三角板按图中的方式叠放,则的度数为( )
A. B. C. D.
8.如图,,四个点在同一直线上,若,则的长是 ( )
A.2 B.3 C.5 D.7
9.在下列条件中:
①∠A+∠B=∠C,②∠A:∠B:∠C=1:2:3,③∠A=2∠B=3∠C,④中,能确定△ABC是直角三角形的条件有( )
A.1个 B.2个 C.3个 D.4个
10.若将长度分别为的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折断),则该三角形的最长边的长为( )
A. B. C. D.
11.下面是投影屏上出示的解答题,需要回答横线上符号代表的内容.
如图,直线直线,在中,,顶点在上,顶点在上,且平分,若,求的度数.
解:∵,,
∴_______①_______,
∵直线直线,
∴_____②______,
∵平分,
∴_____③_____= ,
∵直线直线,
∴___④_____= ,
下列选项错误的是( )
A.①代表64° B.②代表 C.③代表 D.④代表
12.如图,在中,,,,那么的度数为( )
A.64° B.54° C.44° D.36°
13.在中, ,若的平分线交于点,则的度数是( )
A. B. C. D.
14.在△ABC中,,则△ABC是( )
A.等腰直角三角形 B.锐角三角形 C.钝角三角形 D.直角三角形
15.对于题目:如图,是的角平分线,于点,若,求的度数.下面是打乱了的解题过程:①∵;②;③∵平分,∴;④∵,,则下列排序正确的是( ).
A.③④②① B.④②①③ C.③②④① D.③①④②
16.如图,中,,且,,则 的度数为( )
A.80° B.60° C.40° D.20°
二、填空题
17.在中,若,,则的度数为_________.
18.三角形的外角和等于_____度.
三、解答题
19.一个机器人以的速度在平地上按如下要求行走,
(1)该机器人从开始到停止所走过的路程形成的图形是_____;
(2)该机器人从开始到停止所需时间为_______;
(3)若机器人还差就第次回到点处,则它所走过的路程为_____.
20.(1)如图1,的外角为116°,,求的余角的度数.
(2)求图2中的值.
21.如图,,,,求的度数.
22.如图,在中,平分,是的反向延长线上一点,于点.若,,求的度数.
23.已知是的三边长,,设三角形的周长是.
尝试:分别写出及的取值范围.
发现:当为奇数时,求的最大值和最小值.
联想:若是小于18的偶数,判断的形状.
24.如图1,四边形为一张长方形纸片.
(1)如图2,将长方形纸片剪两刀,剪出三个角(),则__________°.
(2)如图3,将长方形纸片剪三刀,剪出四个角(),则__________°.
(3)如图4,将长方形纸片剪四刀,剪出五个角(),则___________°.
(4)根据前面探索出的规律,将本题按照上述剪法剪刀,剪出个角,那么这个角的和是____________°.
25.如图,,其中点在同一条直线上..
(1)若,,求的大小;
(2)若,,求的长.
26.如图,在四边形 中,和分别平分四边形的外角和,与相交于点,若.
(1)如图1,若,求的度数;
(2)如图1,若,试猜想所满足的数量关系式,并说明理由.
(3)如图2,若,判断的位置关系,并说明理由.
参考答案
1.B
【解析】
分析:根据图形全等的定义解答即可.
详解:能够与已知图形重合的只有.故选B.
点睛:本题考查了全等的定义.掌握图形全等的定义是解答的关键.
2.D
【分析】
三角形具有稳定性,其它多边形不具有稳定性,把多边形分割成三角形则多边形的形状就不会改变.
【详解】
赵师傅这样做是运用了三角形的稳定性.
故选:D.
【点睛】
本题考查了三角形稳定性的实际应用.三角形的稳定性在实际生活中有着广泛的应用,如钢架桥、房屋架梁等,因此要使一些图形具有稳定的结构,往往通过连接辅助线转化为三角形而获得.
3.C
【分析】
根据中线的定义解答即可.
【详解】
由题意知,点D是线段AB的中点,
∵AB=8,
∴AD=AB=4,
故选:C.
【点睛】
本题考查三角形的中线,属于基础题型.
4.B
【分析】
根据全等三角形的性质即可求解.
【详解】
解:∵
∴∠ACB=∠DCE
即∠ACD+∠DCB=∠BCE+∠DCB
∴∠ACD=
故选:B.
【点睛】
此题主要考查全等三角形的性质,灵活运用性质是解题关键.
5.A
【分析】
根据题意可知为正六边形一外角,依据多边形外角和为360°进行分析即可.
【详解】
解:∵多边形外角和为360°,
∴正六边形一外角为:360°6=60°,即=60°
故选:A.
【点睛】
本题考查多边形的外角,熟练掌握多边形外角和为360°以及多边形外角的定义是解题的关键.
6.B
【分析】
从三角形的一个顶点向底边作垂线,垂足与顶点之间的线段叫做三角形的高.根据高线的定义即可得出结论.
【详解】
解:A.作出的是△ABC中BC边上的高线,故本选项错误;
B.作出的是△ABC中AB边上的高线,故本选项正确;
C.不能作出△ABC中AB边上的高线,故本选项错误;
D.作出的是△ABC中AC边上的高线,故本选项错误;
故选:B.
【点睛】
本题考查的是作图-基本作图,熟知三角形高线的定义是解答此题的关键.
7.A
【分析】
如图,根据三角板的特点可得∠2与∠3的度数,然后根据三角形的外角性质即得答案.
【详解】
解:如图,∵∠2=45°,∠3=60°,∴∠1=∠2+∠3=105°.
故选:A.
【点睛】
本题以学生常见的三角板为载体,主要考查了三角形的外角性质,属于应知应会题型,熟练掌握三角形的外角性质是解题关键.
8.B
【分析】
根据全等三角形的对应边相等得到EF=BC=8,计算即可.
【详解】
∵△ABC≌△DEF,
∴BC=EF,
又BC=8,
∴EF=8,
∵EC=5,
∵CF=EF-EC=8-5=3.
故选:B.
【点睛】
本题考查了全等三角形的性质,掌握全等三角形的对应边相等、全等三角形的对应角相等是解题的关键.
9.C
【分析】
根据有一个角是直角的三角形是直角三角形进行逐一判断即可.
【详解】
解:①∠A+∠B=∠C,又由∠A+∠B+∠C=180°,得到∠C=90°,所以△ABC是直角三角形;
②∠A:∠B:∠C=1:2:3,根据∠A+∠B+∠C=180°,可得到∠A=30°,∠B=60°,∠C=90°,所以△ABC是直角三角形;
③∠A=2∠B=3∠C,即∠B=∠A,∠C=∠A,所以∠A+∠A+∠A=180°,得到∠A=,由于∠A为最大角,所以△ABC不是直角三角形;
④,即,,得到,所以,所以△ABC是直角三角形;
正确的有3个,
故选:C.
【点睛】
本题考查了直角三角形的定义,找到△ABC中是否有直角是解题的关键.
10.C
【分析】
利用三角形的三边关系列举出所围成三角形的不同情况,通过比较得到结论.
【详解】
①长度分别为7、4、5,能构成三角形,且最长边为7;
②长度分别为8、4、4,不能构成三角形;
③长度分别为8、5、3,不能构成三角形;
④长度分别为9、4、3,不能构成三角形;
综上所述,得到三角形的最长边长为7.
故选:C.
【点睛】
本题考查了三角形的三边关系,利用了三角形中三边的关系求解.注意分类讨论,不重不漏.
11.D
【分析】
先利用三角形内角和定理求得,再根据平行线的性质求得,最后利用角平分线的定义结合平行线的性质即可求解
【详解】
∵,,
∴64,
∵直线直线,
∴,
∵平分,
∴= ,
∵直线直线,
∴ .
∴①代表64°,②代表,③代表,④应该代表.
故选:D.
【点睛】
本题考查了平行线的性质,角平分线的定义以及三角形内角和定理,利用各角之间的关系,找出是解题的关键.
12.B
【分析】
根据平行线的性质和直角三角形的两锐角互余即可求得∠B的度数.
【详解】
∵CD∥AB,∠ACD=36?,
∴∠A=∠ACD=36?,
∵在△ABC中,∠ACB=90?,
∴∠B=90?-∠ACB=90?-36?=54?,
故选:B.
【点睛】
本题考查了平行线的性质、直角三角形的性质,熟知直角三角形的两锐角互余是解答的关键.
13.B
【分析】
由的度数可以求出与的和,由角平分线的性质可以得出,,即可得出与的和,即可得出的度数.
【详解】
∵,
∴+=110°,
∵为与的平分线,
∴,,
∴+=110÷2=55°,
∴=180°-55°=125°.
故选:B.
【点睛】
本题主要考查角平分线的性质以及三角形的内角和定理,熟记相关概念是解题关键.
14.D
【分析】
根据题意,可设∠A=x,表示出∠B,∠C的度数.根据三角形内角和定理列方程求出各角的度数再判断三角形的形状.
【详解】
解:设∠A=x,∵,
∴∠B=2x,∠C=3x,
根据三角形内角和定理得,x+2x+3x=180,
解得 x=30,
则2x=60,3x=90,
即三角形内角分别为30°,60°,90°,
∴此三角形是直角三角形.
故选D.
【点睛】
此题考查三角形内角和定理及判断三角形的形状,属基础题.
15.A
【分析】
根据角平分线、直角三角形的性质计算,即可得到答案.
【详解】
∵平分
∴
∵
∴
∴
∴
故选:A.
【点睛】
本题考查了角平分线、直角三角形的知识;解题的关键是熟练掌握角平分线、直角三角形两锐角互余的性质,从而完成求解.
16.C
【分析】
连接FB,根据三角形内角和和外角知识,进行角度计算即可.
【详解】
解:如图连接FB,
∵,,
∴,
∴,
即,
又∵,
∴,
∵,
∴,
故选:C.
【点睛】
此题考查三角形内角和和外角定义,掌握三角形内角和为180°,三角形一个外角等于不相邻两内角之和是解题关键.
17.
【分析】
根据直角三角形的性质解答即可.
【详解】
∵在Rt△ABC中,∠C=90°,∠B=35°,
∴∠A=90°-35°=55°,
故答案为:55°.
【点睛】
本题考查了直角三角形的性质,关键是根据直角三角形的两锐角互余.
18.360.
【分析】
根据任何多边形的外角和是360度即可求解.
【详解】
解:三角形的外角和等于360°.
故答案是:360.
【点睛】
本题考查三角形外角和的性质,解题关键是根据任何多边形的外角和是360度即可求解.
19.(1)正八边形;(2);(3)
【分析】
(1)该机器人所经过的路径是一个正多边形,利用360°除以45°,即可求得正多边形的边数;
(2)求出多边形的周长,利用周长除以速度即可求得所需时间
(3)求出n次的路径长减去4即可.
【详解】
解:(1)由题意得,该机器人所经过的路径是一个正多边形,
多边形的边数为:360°÷45°=8,
所以,该机器人从开始到停止所走过的路程形成的图形是正八边形,
故答案为:正八边形;
(2)该机器人所走的路程是:4×8=32(m),
则所用时间是:32÷2=16(s).
故答案是:16;
(3)已知机器人n次回到原点的路程为:n×32=32n,
还差4m,即:(32n-4)m.
故答案为:(32n-4)m.
【点睛】
本题考查了正多边形的外角和定理,理解经过的路线是正多边形是关键.
20.(1);(2).
【分析】
(1)根据三角形的外角性质求出∠B,根据余角的概念计算,得到答案;
(2)先求得五边形的内角和,再列出方程即可求解.
【详解】
(1)∵∠B=∠CAD-∠C=116°-80°=36°,
∴∠B的余角=90°-36°=54°;
(2)∵五边形的内角和为540°,
∴,
解得.
【点睛】
本题考查了三角形的外角性质,多边形的内角和,余角的概念,掌握三角形的一个外角等于和它不相邻的两个内角的和以及多边形内角和公式是解题的关键.
21.
【分析】
根据全等三角形的性质得出∠ACB=∠DCB,求出∠ACB,根据三角形内角和定理求出即可.
【详解】
∵△ABC≌△DBC,
∴∠ACB=∠DCB,
∵∠ACD=88°,
∴∠ACB=44°,
∵∠A=40°,
∴∠ABC=180°-∠A-∠ACB=96°.
【点睛】
本题考查了三角形内角和定理和全等三角形的性质,能熟记全等三角形的性质是解此题的关键,注意:全等三角形的对应角相等.
22.
【分析】
根据角平分线的性质得到,求出,利用及三角形的内角和定理求出,根据三角形的外角性质求出,再根据直角三角形的性质求出答案.
【详解】
解:∵平分,
∴,
∵,
∴,,
∵,
∴,
∴,
∵,
∴在中,.
【点睛】
此题考查角平分线的性质,三角形的内角和定理,直角三角形两锐角互余,理解图形中各角度之间的关系是解题的关键.
23.尝试:,;发现:的最大值为,的最小值为;联想:是等腰三角形.
【分析】
尝试:根据三角形三边关系即可得出及的取值范围;
发现:由a、b为偶数,c是奇数可得x也为奇数,利用x的取值范围可知其最大值和最小值;
联想:由x是小于18的偶数和取值范围即可作出判断.
【详解】
解:尝试:∵,
∴,
∴周长的取值范围为;
发现:∵,且为奇数,
∴也为奇数,
∵的范围为,
∴的最大值为19,最小值为13;
联想:∵周长为小于18的偶数,且取值范围为,
∴或,
当为16时,,
当为14时,,
当时,,为等腰三角形;
当时,,为等腰三角形,
综上所述,是等腰三角形.
【点睛】
本题考查了三角形的三边关系、不等式的整数解、等腰三角形的判定,利用三边关系得出第三边的取值范围是解答的关键.
24.(1)360;(2)540;(3)720;(4).
【分析】
(1)过点E作EH∥AB,再根据两直线平行,同旁内角互补即可得到三个角的和等于180°的2倍;
(2)分别过E、F分别作AB的平行线,根据两直线平行,同旁内角互补即可得到四个角的和等于180°的三倍;
(3)分别过E、F、G分别作AB的平行线,根据两直线平行,同旁内角互补即可得到四个角的和等于180°的三倍;
(4)根据前三问个的剪法,剪n刀,剪出n+1个角,那么这n+1个角的和是180n度.
【详解】
(1)过E作EH∥AB(如图②).
∵原四边形是长方形,
∴AB∥CD,
又∵EH∥AB,
∴CD∥EH(平行于同一条直线的两条直线互相平行).
∵EH∥AB,
∴∠A+∠1=180°(两直线平行,同旁内角互补).
∵CD∥EH,
∴∠2+∠C=180°(两直线平行,同旁内角互补).
∴∠A+∠1+∠2+∠C=360°,
又∵∠1+∠2=∠AEC,
∴∠BAE+∠AEC+∠ECD=360°;
(2)分别过E、F分别作AB的平行线,如图③所示,
用上面的方法可得∠BAE+∠AEF+∠EFC+∠FCD=540°;
(3)分别过E、F、G分别作AB的平行线,如图④所示,
用上面的方法可得∠BAE+∠AEF+∠EFG+∠FGC+∠GCD=720°;
(4)由此可得一般规律:剪n刀,剪出n+1个角,那么这n+1个角的和是180n度.
故答案为:(1)360;(2)540;(3)720;(4)180n.
【点睛】
本题主要考查了多边形的内角和,作平行线并利用两直线平行,同旁内角互补是解本题的关键,总结规律求解是本题的难点.
25.(1);(2)3cm.
【分析】
(1)根据垂直的定义及全等三角形的性质得到,即可求出的大小;
(2)利用推出AB=CD,再根据已知得出,即可求出答案.
【详解】
解:(1)∵,
∴,
∵,
∴,
∴.
(2)∵,
∴,
∴,即.
∵,,
∴,
∴.
【点睛】
此题考查三角形全等的性质,垂直的定义,正确理解图形中的对应关系是解题的关键.
26.(1);(2);(3),理由见解析.
【分析】
(1)利用角平分线的定义和四边形的内角和以及α+β=168°推导即可;
(2)利用角平分线的定义和四边形的内角和以及三角形的内角和转化即可;
(3)利用角平分线的定义和四边形的内角和以及三角形的外角的性质计算即可.
【详解】
(1)在四边形ABCD中,∠BAD+∠ABC+∠BCD+∠ADC=360°,
∴∠ABC+∠ADC=360°-(α+β),
∵∠MBC+∠ABC=180°,∠NDC+∠ADC=180°
∴∠MBC+∠NDC=180°-∠ABC+180°-∠ADC=360°-(∠ABC+∠ADC)
=360°-[360°-(α+β)]=α+β,
∵α+β=168°,
∴∠MBC+∠NDC=168°;
(2)β-α=70°
理由:如图1,连接BD,
由(1)有,∠MBC+∠NDC=α+β,
∵BE、DF分别平分四边形的外角∠MBC和∠NDC,
∴∠CBG=∠MBC,∠CDG=∠NDC,
∴∠CBG+∠CDG=∠MBC+∠NDC=(∠MBC+∠NDC)=(α+β),
在△BCD中,∠BDC+∠DBC=180°-∠BCD=180°-β,
在△BDG中,∠BGD=35°,
∴∠GBD+∠GDB+∠BGD=180°,
∴∠CBG+∠CBD+∠CDG+∠BDC+∠BGD=180°,
∴(∠CBG+∠CDG)+(∠BDC+∠CDB)+∠BGD=180°,
∴(α+β)+180°-β+35°=180°,
∴β-α=70°;
(3)平行,
理由:如图2,延长BC交DF于H,
由(1)有,∠MBC+∠NDC=α+β,
∵BE、DF分别平分四边形的外角∠MBC和∠NDC,
∴∠CBE=∠MBC,∠CDH=∠NDC,
∴∠CBE+∠CDH=∠MBC+∠NDC=(∠MBC+∠NDC)=(α+β),
∵∠BCD=∠CDH+∠DHB,
∴∠CDH=∠BCD-∠DHB=β-∠DHB,
∴∠CBE+β-∠DHB=(α+β),
∵α=β,
∴∠CBE+β-∠DHB=(β+β)=β,
∴∠CBE=∠DHB,
∴BE∥DF.
【点睛】
本题主要考查了平角的意义,四边形的内角和,三角形内角和,三角形的外角性质,角平分线的意义,用整体代换的思想是解本题的关键.
同课章节目录
