河北省张家口市宣化区2019-2020学年八年级上学期期末考试数学试题(Word版,附答案解析)
文档属性
| 名称 | 河北省张家口市宣化区2019-2020学年八年级上学期期末考试数学试题(Word版,附答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 649.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 14:45:33 | ||
图片预览


文档简介
河北省张家口市宣化区2019-2020学年八年级上学期期末考试数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列代数式中,属于分式的是( )
A.-3 B. C. D.
2.8的平方根是()
A.4 B.±4 C.2 D.
3.如图,△AOC≌△BOD,点A与点B是对应点,那么下列结论中错误的是( )
A.AB=CD B.AC=BD C.AO=BO D.∠A=∠B
4.下列四组线段中,可以构成直角三角形的是( )
A.4,5,6 B.1.5,2,2.5 C.2,3,4 D.1,, 3
5.化简的结果是( )
A. B. C. D.1
6.下列运算中错误的是( )
A. B. C. D.
7.一等腰三角形的两边长x、y满足方程组则此等腰三角形的周长为?( )
A.5 B.4 C.3 D.5或4
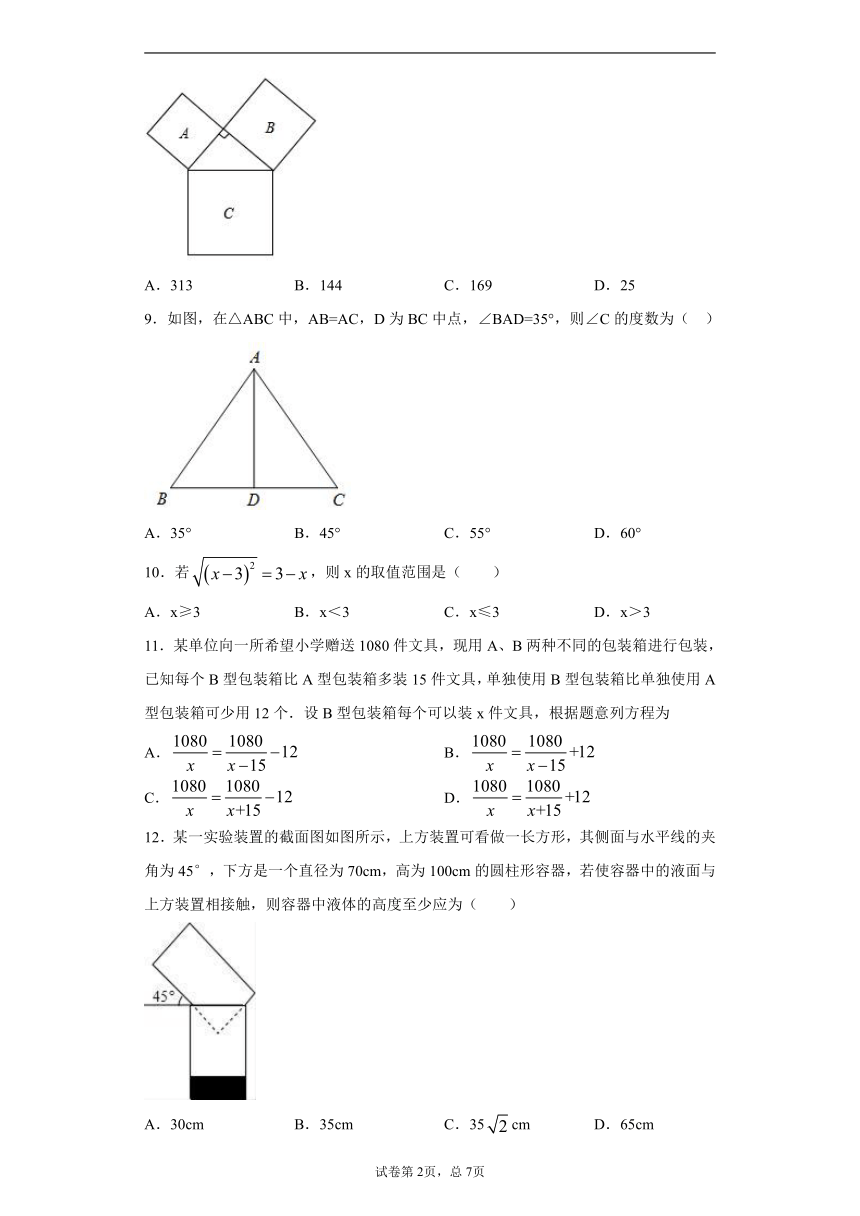
8.如图,已知正方形B的面积为144,正方形C的面积为169时,那么正方形A的面积为( )
A.313 B.144 C.169 D.25
9.如图,在△ABC中,AB=AC,D为BC中点,∠BAD=35°,则∠C的度数为( )
A.35° B.45° C.55° D.60°
10.若,则x的取值范围是( )
A.x≥3 B.x<3 C.x≤3 D.x>3
11.某单位向一所希望小学赠送1080件文具,现用A、B两种不同的包装箱进行包装,已知每个B型包装箱比A型包装箱多装15件文具,单独使用B型包装箱比单独使用A型包装箱可少用12个.设B型包装箱每个可以装x件文具,根据题意列方程为
A. B.
C. D.
12.某一实验装置的截面图如图所示,上方装置可看做一长方形,其侧面与水平线的夹角为45°,下方是一个直径为70cm,高为100cm的圆柱形容器,若使容器中的液面与上方装置相接触,则容器中液体的高度至少应为( )
A.30cm B.35cm C.35cm D.65cm
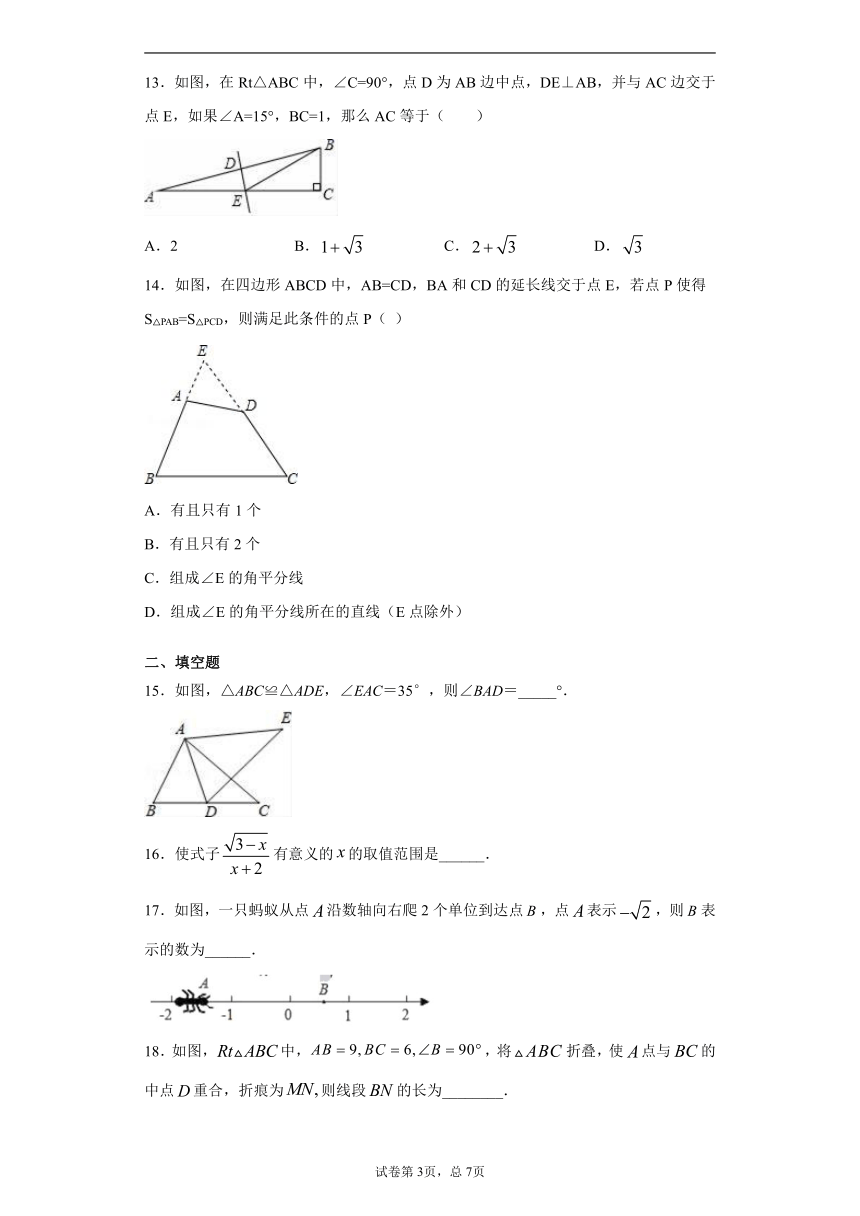
13.如图,在Rt△ABC中,∠C=90°,点D为AB边中点,DE⊥AB,并与AC边交于点E,如果∠A=15°,BC=1,那么AC等于( )
A.2 B. C. D.
14.如图,在四边形ABCD中,AB=CD,BA和CD的延长线交于点E,若点P使得S△PAB=S△PCD,则满足此条件的点P( )
A.有且只有1个
B.有且只有2个
C.组成∠E的角平分线
D.组成∠E的角平分线所在的直线(E点除外)
二、填空题
15.如图,△ABC≌△ADE,∠EAC=35°,则∠BAD=_____°.
16.使式子有意义的的取值范围是______.
17.如图,一只蚂蚁从点沿数轴向右爬2个单位到达点,点表示,则表示的数为______.
18.如图,中,,将折叠,使点与的中点重合,折痕为则线段的长为________.
19.如图,在中,,,以为圆心,任意长为半径画弧分别交、于点和,再分别以、为圆心,大于的长为半径画弧,两弧交于点,连结并延长交于点,则下列说法①是的平分线;②;③点在的中垂线上;正确的个数是______个.
20.下面是一个按某种规律排列的数表:
第1行
1
第2行
2
第3行
第4行
…
…
那么第n(,且n是整数)行的第2个数是________.(用含n的代数式表示)
三、解答题
21.计算
(1)解方程:
(2)
22.在如图所示的方格纸中,每个方格都是边长为1个单位的小正方形,的三个顶点都在格点上(每个小正方形的顶点叫做格点).
(1)画出关于直线l对称的图形.
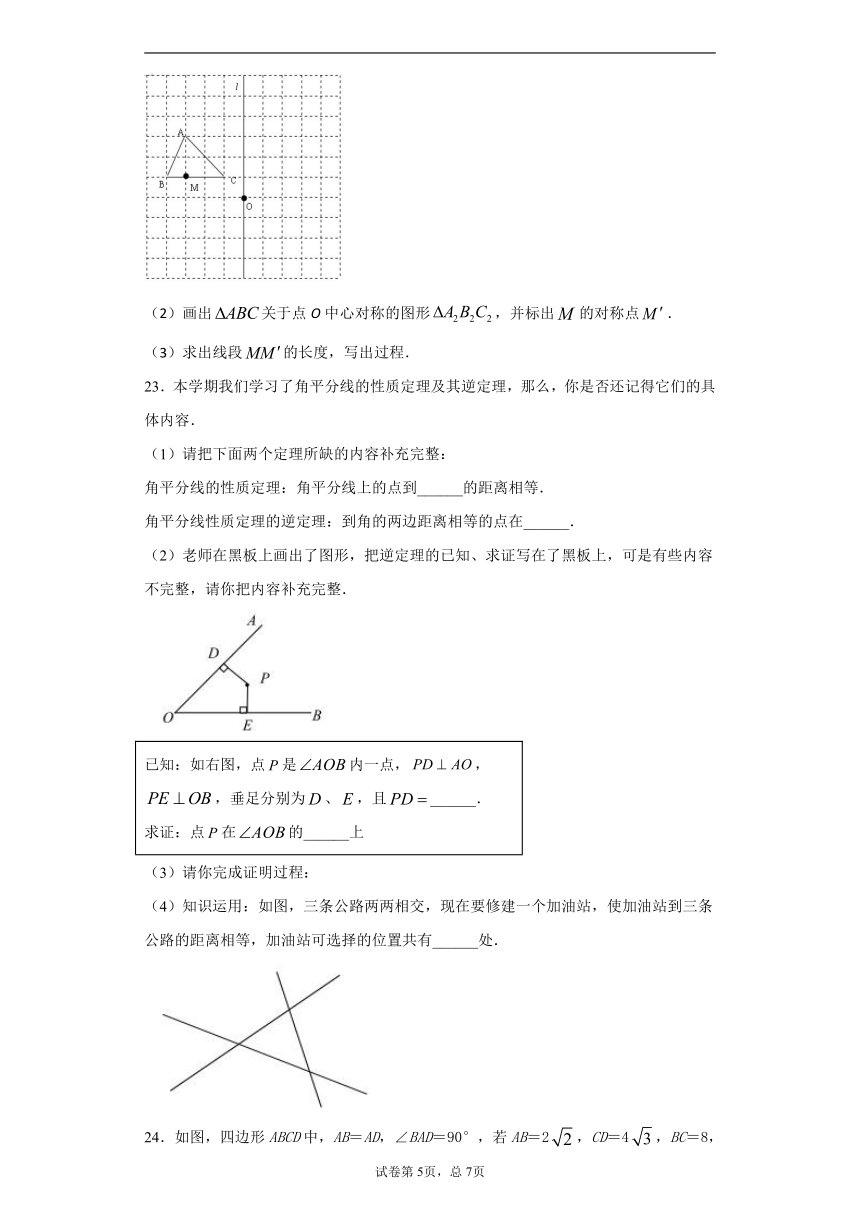
(2)画出关于点O中心对称的图形,并标出的对称点.
(3)求出线段的长度,写出过程.
23.本学期我们学习了角平分线的性质定理及其逆定理,那么,你是否还记得它们的具体内容.
(1)请把下面两个定理所缺的内容补充完整:
角平分线的性质定理:角平分线上的点到______的距离相等.
角平分线性质定理的逆定理:到角的两边距离相等的点在______.
(2)老师在黑板上画出了图形,把逆定理的已知、求证写在了黑板上,可是有些内容不完整,请你把内容补充完整.
已知:如右图,点是内一点,,,垂足分别为、,且______.
求证:点在的______上
(3)请你完成证明过程:
(4)知识运用:如图,三条公路两两相交,现在要修建一个加油站,使加油站到三条公路的距离相等,加油站可选择的位置共有______处.
24.如图,四边形ABCD中,AB=AD,∠BAD=90°,若AB=2,CD=4,BC=8,求四边形ABCD的面积.
25.阅读理解
(发现)如果记,并且f(1)表示当x=1时的值,则f(1)=______;
表示当时的值,则______;
表示当时的值,则=______;
表示当时的值,则______;
表示当时的值,则______;
(拓展)试计算的值.
26.八年级一班数学兴趣小组在一次活动中进行了探究试验活动,请你和他们一起活动吧.
(探究与发现)
(1)如图1,是的中线,延长至点,使,连接,写出图中全等的两个三角形______
(理解与应用)
(2)填空:如图2,是的中线,若,,设,则的取值范围是______.
(3)已知:如图3,是的中线,,点在的延长线上,,求证:.
参考答案
1.C
【分析】
判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式.
【详解】
解: -3;;是整式;符合分式的概念,是分式
故选:C
【点睛】
本题主要考查分式的概念,分式与整式的区别主要在于:分母中是否含有未知数.
2.D
【分析】
直接根据平方根的定义进行解答即可解决问题.
【详解】
∵(±2)2=8,
∴8的平方根是±2.
故选D.
【点睛】
本题考查了平方根的定义.注意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.
3.A
【分析】
根据全等三角形的对应边、对应角相等,可得出正确的结论,可得出答案.
【详解】
∵△AOC≌△BOD,
∴∠A=∠B,AO=BO,AC=BD,
∴B、C、D均正确,
而AB、CD不是不是对应边,且CO≠AO,
∴AB≠CD,
故选A.
【点睛】
本题主要考查全等三角形的性质,掌握全等三角形的对应边、角相等是解题的关键.
4.B
【解析】
试题分析:由勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方即可:
A、42+52=41≠62,不可以构成直角三角形,故本选项错误;
B、1.52+22=6.25=2.52,可以构成直角三角形,故本选项正确;
C、22+32=13≠42,不可以构成直角三角形,故本选项错误;
D、,不可以构成直角三角形,故本选项错误.
故选B.
考点:勾股定理的逆定理.
5.B
【分析】
按照同分母分式的减法运算法则进行计算,分母不变,分子相减,结果能约分要约分成最简分式.
【详解】
解:
故选:B.
【点睛】
本题考查同分母分式的加减法,题目比较基础,掌握运算法则正确因式分解将计算结果进行约分是解题关键.
6.A
【分析】
根据合并同类二次根式的法则对A进行判断;根据二次根式的乘法法则对B进行判断;根据二次根式的除法法则对C进行判断;根据二次根式的性质对D进行判断.
【详解】
A. 与不是同类二次根式,不能合并,故此项错误,符合要求;
B. ,故此项正确,不符合要求;
C. ,故此项正确,不符合要求;
D. ,故此项正确,不符合要求;
故选A.
【点睛】
本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.
7.A
【分析】
先解二元一次方程组,然后讨论腰长的大小,再根据三角形三边关系即可得出答案.
【详解】
解:解方程组,得,
所以等腰三角形的两边长为2,1.
若腰长为1,底边长为2,由知,这样的三角形不存在.
若腰长为2,底边长为1,则三角形的周长为5.
所以,这个等腰三角形的周长为5.
故选:A.
【点睛】
本题考查了等腰三角形的性质及解二元一次方程组,难度一般,关键是掌握分类讨论的思想解题.
8.D
【分析】
设三个正方形的边长依次为,由于三个正方形的三边组成一个直角三角形,利用勾股定理即可解答.
【详解】
设三个正方形的边长依次为,由于三个正方形的三边组成一个直角三角形,
所以,
故,
即.
故选:D
9.C
【解析】
试题分析:根据等腰三角形的三线合一的性质可直接得到AD平分∠BAC,AD⊥BC,因此∠DAC=∠BAD=35°,∠ADC=90°,从而可求得∠C=55°.
故选C
考点:等腰三角形三线合一
10.C
【分析】
根据二次根式的非负性解答即可.
【详解】
∵,而,
∴,,解得:,
故选C.
【点睛】
本题考查绝对值、二次根式的非负性,理解绝对值的意义是关键.
11.A
【分析】
关键描述语:单独使用B型包装箱比单独使用A型包装箱可少用12个;可列等量关系为:所用B型包装箱的数量=所用A型包装箱的数量-12,由此可得到所求的方程.
【详解】
解:根据题意,得:
故选:A.
【点睛】
此题考查分式方程的问题,关键是根据公式:包装箱的个数与文具的总个数÷每个包装箱装的文具个数是等量关系解答.
12.D
【分析】
由题意可知,进入容器内的三角形可看作是一个斜边为70cm的等腰直角三角形,由等腰三角形三线合一的性质可得到高,即可求出答案.
【详解】
由题意可知,进入容器内的三角形可看作是一个斜边为70cm的等腰直角三角形,
由等腰三角形三线合一的性质可得到高斜边上的高应该为35cm,
使容器中的液面与上方装置相接触,容器中液体的高度至少应为100﹣35=65cm.
故选D.
考点:等腰直角三角形.
13.C
【分析】
根据线段垂直平分线的性质得到AE=BE,根据等腰三角形的性质得到∠ABE=∠A=15°,利用三角形外角的性质求得∠BEC =30°,再根据30°角直角三角形的性质即可求得结论.
【详解】
∵点D为AB边中点,DE⊥AB,
∴DE垂直平分AB,
∴AE=BE,
∴∠ABE=∠A=15°,
∴∠BEC=∠A+∠ABE=30°,
∵∠C=90°,
∴BE=AE=2BC=2,CE=BC=,
∴AC=AE+CE=2+,
故选C.
【点睛】
本题考查了线段垂直平分线的性质、等腰三角形的性质、30°角直角三角形的性质,熟练掌握线段垂直平分线的性质是解题的关键.
14.D
【解析】
试题分析:作∠E的平分线,可得点P到AB和CD的距离相等,因为AB=CD,所以此时点P满足S△PAB=S△PCD.
故选D.
考点:角平分线的性质.
15.35
【解析】
由全等三角形的性质知:对应角∠CAB=∠EAD相等,求出∠CAB=∠EAD,待入求出即可.
解:∵△ABC≌△ADE,
∴∠CAB=∠EAD,
∵∠EAC=∠CAB-∠EAB,∠BAD=∠EAD-∠EAB,
∴∠BAD=∠EAC,
∴∠BAD=∠EAC=35°.
故答案为:35.
16.且
【分析】
根据分式的分母不能为0、二次根式的被开方数大于或等于0列出式子求解即可得.
【详解】
由题意得:,
解得且,
故答案为:且.
【点睛】
本题考查了分式和二次根式有意义的条件,熟练掌握分式和二次根式的定义是解题关键.
17..
【分析】
根据平移的性质得出答案即可.
【详解】
解:蚂蚁从点沿数轴向右爬2个单位到达点,点表示,
根据题意得,表示的数为:,
故答案是:.
【点睛】
本题考查了数轴上的点的平移,熟悉相关性质是解题的关键.
18.4
【分析】
根据题意,设BN=x,由折叠DN=AN=9-x,在利用勾股定理列方程解出x,就求出BN的长.
【详解】
∵D是CB中点,BC=6
∴BD=3
设BN=x,AN=9-x,由折叠,DN=AN=9-x,
在中,,
,解得x=4
∴BN=4.
故答案是:4.
【点睛】
本题考查折叠的性质和勾股定理,关键是利用方程思想设边长,然后用勾股定理列方程解未知数,求边长.
19.3
【分析】
根据角平分线的做法可得①正确,再根据三角形内角和定理和外角与内角的关系可得∠ADC=60°,再根据线段垂直平分线的性质逆定理可得③正确.
【详解】
解:①根据角平分线的做法可得AD是∠BAC的平分线,说法①正确;
②∵∠C=90°,∠B=30°,
∴∠CAB=60°,
∵AD平分∠CAB,
∴∠DAB=30°,
∴∠ADC=30°+30°=60°,
因此∠ADC=60°正确;
③∵∠DAB=30°,∠B=30°,
∴AD=BD,
∴点D在AB的中垂线上,故③说法正确,
故答案为:3.
【点睛】
此题主要考查了角平分线的做法以及垂直平分线的判定,熟练根据角平分线的性质得出∠ADC度数是解题关键.
20.
【分析】
根据每一行的最后一个数的被开方数是所在的行数的平方,写出第行的最后一个数的平方是,据此可写出答案.
【详解】
第2行最后一个数字是:,
第3行最后一个数字是:,
第4行最后一个数字是:,
第行最后一个数字是:,
第行第一个数字是:,
第行第二个数字是:,
故答案为:
【点睛】
本题考查了规律型-数字变化,解题的关键是确定每一行最后一个数字.
21.(1);(2).
【分析】
(1)两边同时乘最简公分母可把分式方程化为整式方程来解答;
(2)利用零指数幂、算术平方根的知识化简,再根据实数的运算法则计算即可.
【详解】
解:(1)
去分母,得.
去括号,得
解得,
经检验,是原方程的解;
(2)
【点睛】
本题考查了实数的混合运算和解分式方程,熟悉相关性质,并对分式方程进行检验是解题的关键,.
22.(1)详见解析;(2)详见解析;(3)
【分析】
(1)根据网格结构找出点A、B、C关于直线l的对称点A1、B1、C1的位置,然后顺次连接即可;
(2)根据网格结构找出点A、B、C关于点O中心对称的点A2、B2、C2的位置,然后顺次连接即可;
(3)利用勾股定理列式计算即可得解.
【详解】
(1)如图:
(2)如图 :
(3)过点M竖直向下作射线,过点M'水平向左作射线,
两条线相交于点N,可知∠MNM'是直角,在RtΔMNM'中,
由勾股定理得MN2+NM'2=MM'2,
因为MN=2,M'N=5,
所以MM'=
【点睛】
本题考查了利用轴对称变换作图,利用旋转变换作图,熟练掌握网格结构,准确找出对应点的位置是解题的关键.
23.(1)这个角的两边,角平分线上;(2)PE,平分线上;(3)见解析;(4)4
【分析】
(1)根据角平分线的性质定理和判定定理解答;
(2)根据题意结合图形写出已知;
(3)作射线OP,证明Rt△OPD≌Rt△OPE即可;
(4)根据角平分线的性质定理解答.
【详解】
解:(1)角平分线性质定理:角平分线上的点到这个角的两边的距离相等.
角平分线判定定理:到角的两边距离相等的点在角平分线上,
故答案为:这个角的两边;角平分线上;
(2)已知:如图1,点P是∠AOB内一点,PD⊥AO,PE⊥OB,垂足分别为D、E,且PD=PE,求证:点P在∠AOB的平分线上.
故答案为:PE;平分线上;
(3)如图:作射线,
,,
在和中,
∴
∴
∴是的平分线,即点在的平分线上.
(4)如图2,M、N、G、H即为所求,
故答案为:4.
【点睛】
本题考查的是角平分线的性质定理和判定定理的应用,掌握角的平分线上的点到角的两边的距离相等、到角的两边距离相等的点在角平分线上是解题的关键.
24.4+8.
【解析】
试题分析:先根据勾股定理求出BD的长,再根据勾股定理求得BC的长,四边形ABCD的面积是两个直角三角形的面积之和.
试题解析:
∵ AB=AD,∠BAD=90°,AB=,
∴ BD==4,
∵ BD2+CD2=42+()2=64,BC2=64,
∴ BD2+CD2=BC2,
∴ △BCD为直角三角形,
∴S四边形ABCD=S△ABD+S△BCD=××+××4=4+8.
25.,,,,;2012.5
【分析】
(1)【发现】分别把x=1、2、 、3、 代入即可得出答案
(2)【拓展】根据f的变化规律得到然后求解即可.
【详解】
解:【发现】;
;;
;
【拓展】
∵
∴
∴
∴
【点睛】
本题考查了函数值,数字变化规律,读懂题目信息,理解变化规律f的方法并确定出是解题的关键.
26.(1);(2);(3)见解析
【分析】
(1)根据全等三角形的判定即可得到结论;
(2)延长至点,使,连接,根据全等三角形的性质得到,根据三角形的三边关系即可得到结论;
(3)延长到,使,连接,于是得到由已知条件得到,根据全等三角形的性质得到,,于是得到,推出,根据全等三角形的性质即可得到结论.
【详解】
(1)证明:在与中,
,
;
故答案为:;
(2)解:如图2,延长至点,使,连接,
在与中,
,
,
,
在中,,
即,
的取值范围是;
故答案为:;
(3)证明:如图3,延长到,使,连接,
,
是的中线,
,
在与中,
,
,
,,
,
,,
,,
,
,
,
在与中,
,
,
.
【点睛】
本题考查了全等三角形的判定和性质,三角形的中线的定义,三角形的三边关系,正确的作出图形是解题的关键.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列代数式中,属于分式的是( )
A.-3 B. C. D.
2.8的平方根是()
A.4 B.±4 C.2 D.
3.如图,△AOC≌△BOD,点A与点B是对应点,那么下列结论中错误的是( )
A.AB=CD B.AC=BD C.AO=BO D.∠A=∠B
4.下列四组线段中,可以构成直角三角形的是( )
A.4,5,6 B.1.5,2,2.5 C.2,3,4 D.1,, 3
5.化简的结果是( )
A. B. C. D.1
6.下列运算中错误的是( )
A. B. C. D.
7.一等腰三角形的两边长x、y满足方程组则此等腰三角形的周长为?( )
A.5 B.4 C.3 D.5或4
8.如图,已知正方形B的面积为144,正方形C的面积为169时,那么正方形A的面积为( )
A.313 B.144 C.169 D.25
9.如图,在△ABC中,AB=AC,D为BC中点,∠BAD=35°,则∠C的度数为( )
A.35° B.45° C.55° D.60°
10.若,则x的取值范围是( )
A.x≥3 B.x<3 C.x≤3 D.x>3
11.某单位向一所希望小学赠送1080件文具,现用A、B两种不同的包装箱进行包装,已知每个B型包装箱比A型包装箱多装15件文具,单独使用B型包装箱比单独使用A型包装箱可少用12个.设B型包装箱每个可以装x件文具,根据题意列方程为
A. B.
C. D.
12.某一实验装置的截面图如图所示,上方装置可看做一长方形,其侧面与水平线的夹角为45°,下方是一个直径为70cm,高为100cm的圆柱形容器,若使容器中的液面与上方装置相接触,则容器中液体的高度至少应为( )
A.30cm B.35cm C.35cm D.65cm
13.如图,在Rt△ABC中,∠C=90°,点D为AB边中点,DE⊥AB,并与AC边交于点E,如果∠A=15°,BC=1,那么AC等于( )
A.2 B. C. D.
14.如图,在四边形ABCD中,AB=CD,BA和CD的延长线交于点E,若点P使得S△PAB=S△PCD,则满足此条件的点P( )
A.有且只有1个
B.有且只有2个
C.组成∠E的角平分线
D.组成∠E的角平分线所在的直线(E点除外)
二、填空题
15.如图,△ABC≌△ADE,∠EAC=35°,则∠BAD=_____°.
16.使式子有意义的的取值范围是______.
17.如图,一只蚂蚁从点沿数轴向右爬2个单位到达点,点表示,则表示的数为______.
18.如图,中,,将折叠,使点与的中点重合,折痕为则线段的长为________.
19.如图,在中,,,以为圆心,任意长为半径画弧分别交、于点和,再分别以、为圆心,大于的长为半径画弧,两弧交于点,连结并延长交于点,则下列说法①是的平分线;②;③点在的中垂线上;正确的个数是______个.
20.下面是一个按某种规律排列的数表:
第1行
1
第2行
2
第3行
第4行
…
…
那么第n(,且n是整数)行的第2个数是________.(用含n的代数式表示)
三、解答题
21.计算
(1)解方程:
(2)
22.在如图所示的方格纸中,每个方格都是边长为1个单位的小正方形,的三个顶点都在格点上(每个小正方形的顶点叫做格点).
(1)画出关于直线l对称的图形.
(2)画出关于点O中心对称的图形,并标出的对称点.
(3)求出线段的长度,写出过程.
23.本学期我们学习了角平分线的性质定理及其逆定理,那么,你是否还记得它们的具体内容.
(1)请把下面两个定理所缺的内容补充完整:
角平分线的性质定理:角平分线上的点到______的距离相等.
角平分线性质定理的逆定理:到角的两边距离相等的点在______.
(2)老师在黑板上画出了图形,把逆定理的已知、求证写在了黑板上,可是有些内容不完整,请你把内容补充完整.
已知:如右图,点是内一点,,,垂足分别为、,且______.
求证:点在的______上
(3)请你完成证明过程:
(4)知识运用:如图,三条公路两两相交,现在要修建一个加油站,使加油站到三条公路的距离相等,加油站可选择的位置共有______处.
24.如图,四边形ABCD中,AB=AD,∠BAD=90°,若AB=2,CD=4,BC=8,求四边形ABCD的面积.
25.阅读理解
(发现)如果记,并且f(1)表示当x=1时的值,则f(1)=______;
表示当时的值,则______;
表示当时的值,则=______;
表示当时的值,则______;
表示当时的值,则______;
(拓展)试计算的值.
26.八年级一班数学兴趣小组在一次活动中进行了探究试验活动,请你和他们一起活动吧.
(探究与发现)
(1)如图1,是的中线,延长至点,使,连接,写出图中全等的两个三角形______
(理解与应用)
(2)填空:如图2,是的中线,若,,设,则的取值范围是______.
(3)已知:如图3,是的中线,,点在的延长线上,,求证:.
参考答案
1.C
【分析】
判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式.
【详解】
解: -3;;是整式;符合分式的概念,是分式
故选:C
【点睛】
本题主要考查分式的概念,分式与整式的区别主要在于:分母中是否含有未知数.
2.D
【分析】
直接根据平方根的定义进行解答即可解决问题.
【详解】
∵(±2)2=8,
∴8的平方根是±2.
故选D.
【点睛】
本题考查了平方根的定义.注意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.
3.A
【分析】
根据全等三角形的对应边、对应角相等,可得出正确的结论,可得出答案.
【详解】
∵△AOC≌△BOD,
∴∠A=∠B,AO=BO,AC=BD,
∴B、C、D均正确,
而AB、CD不是不是对应边,且CO≠AO,
∴AB≠CD,
故选A.
【点睛】
本题主要考查全等三角形的性质,掌握全等三角形的对应边、角相等是解题的关键.
4.B
【解析】
试题分析:由勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方即可:
A、42+52=41≠62,不可以构成直角三角形,故本选项错误;
B、1.52+22=6.25=2.52,可以构成直角三角形,故本选项正确;
C、22+32=13≠42,不可以构成直角三角形,故本选项错误;
D、,不可以构成直角三角形,故本选项错误.
故选B.
考点:勾股定理的逆定理.
5.B
【分析】
按照同分母分式的减法运算法则进行计算,分母不变,分子相减,结果能约分要约分成最简分式.
【详解】
解:
故选:B.
【点睛】
本题考查同分母分式的加减法,题目比较基础,掌握运算法则正确因式分解将计算结果进行约分是解题关键.
6.A
【分析】
根据合并同类二次根式的法则对A进行判断;根据二次根式的乘法法则对B进行判断;根据二次根式的除法法则对C进行判断;根据二次根式的性质对D进行判断.
【详解】
A. 与不是同类二次根式,不能合并,故此项错误,符合要求;
B. ,故此项正确,不符合要求;
C. ,故此项正确,不符合要求;
D. ,故此项正确,不符合要求;
故选A.
【点睛】
本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.
7.A
【分析】
先解二元一次方程组,然后讨论腰长的大小,再根据三角形三边关系即可得出答案.
【详解】
解:解方程组,得,
所以等腰三角形的两边长为2,1.
若腰长为1,底边长为2,由知,这样的三角形不存在.
若腰长为2,底边长为1,则三角形的周长为5.
所以,这个等腰三角形的周长为5.
故选:A.
【点睛】
本题考查了等腰三角形的性质及解二元一次方程组,难度一般,关键是掌握分类讨论的思想解题.
8.D
【分析】
设三个正方形的边长依次为,由于三个正方形的三边组成一个直角三角形,利用勾股定理即可解答.
【详解】
设三个正方形的边长依次为,由于三个正方形的三边组成一个直角三角形,
所以,
故,
即.
故选:D
9.C
【解析】
试题分析:根据等腰三角形的三线合一的性质可直接得到AD平分∠BAC,AD⊥BC,因此∠DAC=∠BAD=35°,∠ADC=90°,从而可求得∠C=55°.
故选C
考点:等腰三角形三线合一
10.C
【分析】
根据二次根式的非负性解答即可.
【详解】
∵,而,
∴,,解得:,
故选C.
【点睛】
本题考查绝对值、二次根式的非负性,理解绝对值的意义是关键.
11.A
【分析】
关键描述语:单独使用B型包装箱比单独使用A型包装箱可少用12个;可列等量关系为:所用B型包装箱的数量=所用A型包装箱的数量-12,由此可得到所求的方程.
【详解】
解:根据题意,得:
故选:A.
【点睛】
此题考查分式方程的问题,关键是根据公式:包装箱的个数与文具的总个数÷每个包装箱装的文具个数是等量关系解答.
12.D
【分析】
由题意可知,进入容器内的三角形可看作是一个斜边为70cm的等腰直角三角形,由等腰三角形三线合一的性质可得到高,即可求出答案.
【详解】
由题意可知,进入容器内的三角形可看作是一个斜边为70cm的等腰直角三角形,
由等腰三角形三线合一的性质可得到高斜边上的高应该为35cm,
使容器中的液面与上方装置相接触,容器中液体的高度至少应为100﹣35=65cm.
故选D.
考点:等腰直角三角形.
13.C
【分析】
根据线段垂直平分线的性质得到AE=BE,根据等腰三角形的性质得到∠ABE=∠A=15°,利用三角形外角的性质求得∠BEC =30°,再根据30°角直角三角形的性质即可求得结论.
【详解】
∵点D为AB边中点,DE⊥AB,
∴DE垂直平分AB,
∴AE=BE,
∴∠ABE=∠A=15°,
∴∠BEC=∠A+∠ABE=30°,
∵∠C=90°,
∴BE=AE=2BC=2,CE=BC=,
∴AC=AE+CE=2+,
故选C.
【点睛】
本题考查了线段垂直平分线的性质、等腰三角形的性质、30°角直角三角形的性质,熟练掌握线段垂直平分线的性质是解题的关键.
14.D
【解析】
试题分析:作∠E的平分线,可得点P到AB和CD的距离相等,因为AB=CD,所以此时点P满足S△PAB=S△PCD.
故选D.
考点:角平分线的性质.
15.35
【解析】
由全等三角形的性质知:对应角∠CAB=∠EAD相等,求出∠CAB=∠EAD,待入求出即可.
解:∵△ABC≌△ADE,
∴∠CAB=∠EAD,
∵∠EAC=∠CAB-∠EAB,∠BAD=∠EAD-∠EAB,
∴∠BAD=∠EAC,
∴∠BAD=∠EAC=35°.
故答案为:35.
16.且
【分析】
根据分式的分母不能为0、二次根式的被开方数大于或等于0列出式子求解即可得.
【详解】
由题意得:,
解得且,
故答案为:且.
【点睛】
本题考查了分式和二次根式有意义的条件,熟练掌握分式和二次根式的定义是解题关键.
17..
【分析】
根据平移的性质得出答案即可.
【详解】
解:蚂蚁从点沿数轴向右爬2个单位到达点,点表示,
根据题意得,表示的数为:,
故答案是:.
【点睛】
本题考查了数轴上的点的平移,熟悉相关性质是解题的关键.
18.4
【分析】
根据题意,设BN=x,由折叠DN=AN=9-x,在利用勾股定理列方程解出x,就求出BN的长.
【详解】
∵D是CB中点,BC=6
∴BD=3
设BN=x,AN=9-x,由折叠,DN=AN=9-x,
在中,,
,解得x=4
∴BN=4.
故答案是:4.
【点睛】
本题考查折叠的性质和勾股定理,关键是利用方程思想设边长,然后用勾股定理列方程解未知数,求边长.
19.3
【分析】
根据角平分线的做法可得①正确,再根据三角形内角和定理和外角与内角的关系可得∠ADC=60°,再根据线段垂直平分线的性质逆定理可得③正确.
【详解】
解:①根据角平分线的做法可得AD是∠BAC的平分线,说法①正确;
②∵∠C=90°,∠B=30°,
∴∠CAB=60°,
∵AD平分∠CAB,
∴∠DAB=30°,
∴∠ADC=30°+30°=60°,
因此∠ADC=60°正确;
③∵∠DAB=30°,∠B=30°,
∴AD=BD,
∴点D在AB的中垂线上,故③说法正确,
故答案为:3.
【点睛】
此题主要考查了角平分线的做法以及垂直平分线的判定,熟练根据角平分线的性质得出∠ADC度数是解题关键.
20.
【分析】
根据每一行的最后一个数的被开方数是所在的行数的平方,写出第行的最后一个数的平方是,据此可写出答案.
【详解】
第2行最后一个数字是:,
第3行最后一个数字是:,
第4行最后一个数字是:,
第行最后一个数字是:,
第行第一个数字是:,
第行第二个数字是:,
故答案为:
【点睛】
本题考查了规律型-数字变化,解题的关键是确定每一行最后一个数字.
21.(1);(2).
【分析】
(1)两边同时乘最简公分母可把分式方程化为整式方程来解答;
(2)利用零指数幂、算术平方根的知识化简,再根据实数的运算法则计算即可.
【详解】
解:(1)
去分母,得.
去括号,得
解得,
经检验,是原方程的解;
(2)
【点睛】
本题考查了实数的混合运算和解分式方程,熟悉相关性质,并对分式方程进行检验是解题的关键,.
22.(1)详见解析;(2)详见解析;(3)
【分析】
(1)根据网格结构找出点A、B、C关于直线l的对称点A1、B1、C1的位置,然后顺次连接即可;
(2)根据网格结构找出点A、B、C关于点O中心对称的点A2、B2、C2的位置,然后顺次连接即可;
(3)利用勾股定理列式计算即可得解.
【详解】
(1)如图:
(2)如图 :
(3)过点M竖直向下作射线,过点M'水平向左作射线,
两条线相交于点N,可知∠MNM'是直角,在RtΔMNM'中,
由勾股定理得MN2+NM'2=MM'2,
因为MN=2,M'N=5,
所以MM'=
【点睛】
本题考查了利用轴对称变换作图,利用旋转变换作图,熟练掌握网格结构,准确找出对应点的位置是解题的关键.
23.(1)这个角的两边,角平分线上;(2)PE,平分线上;(3)见解析;(4)4
【分析】
(1)根据角平分线的性质定理和判定定理解答;
(2)根据题意结合图形写出已知;
(3)作射线OP,证明Rt△OPD≌Rt△OPE即可;
(4)根据角平分线的性质定理解答.
【详解】
解:(1)角平分线性质定理:角平分线上的点到这个角的两边的距离相等.
角平分线判定定理:到角的两边距离相等的点在角平分线上,
故答案为:这个角的两边;角平分线上;
(2)已知:如图1,点P是∠AOB内一点,PD⊥AO,PE⊥OB,垂足分别为D、E,且PD=PE,求证:点P在∠AOB的平分线上.
故答案为:PE;平分线上;
(3)如图:作射线,
,,
在和中,
∴
∴
∴是的平分线,即点在的平分线上.
(4)如图2,M、N、G、H即为所求,
故答案为:4.
【点睛】
本题考查的是角平分线的性质定理和判定定理的应用,掌握角的平分线上的点到角的两边的距离相等、到角的两边距离相等的点在角平分线上是解题的关键.
24.4+8.
【解析】
试题分析:先根据勾股定理求出BD的长,再根据勾股定理求得BC的长,四边形ABCD的面积是两个直角三角形的面积之和.
试题解析:
∵ AB=AD,∠BAD=90°,AB=,
∴ BD==4,
∵ BD2+CD2=42+()2=64,BC2=64,
∴ BD2+CD2=BC2,
∴ △BCD为直角三角形,
∴S四边形ABCD=S△ABD+S△BCD=××+××4=4+8.
25.,,,,;2012.5
【分析】
(1)【发现】分别把x=1、2、 、3、 代入即可得出答案
(2)【拓展】根据f的变化规律得到然后求解即可.
【详解】
解:【发现】;
;;
;
【拓展】
∵
∴
∴
∴
【点睛】
本题考查了函数值,数字变化规律,读懂题目信息,理解变化规律f的方法并确定出是解题的关键.
26.(1);(2);(3)见解析
【分析】
(1)根据全等三角形的判定即可得到结论;
(2)延长至点,使,连接,根据全等三角形的性质得到,根据三角形的三边关系即可得到结论;
(3)延长到,使,连接,于是得到由已知条件得到,根据全等三角形的性质得到,,于是得到,推出,根据全等三角形的性质即可得到结论.
【详解】
(1)证明:在与中,
,
;
故答案为:;
(2)解:如图2,延长至点,使,连接,
在与中,
,
,
,
在中,,
即,
的取值范围是;
故答案为:;
(3)证明:如图3,延长到,使,连接,
,
是的中线,
,
在与中,
,
,
,,
,
,,
,,
,
,
,
在与中,
,
,
.
【点睛】
本题考查了全等三角形的判定和性质,三角形的中线的定义,三角形的三边关系,正确的作出图形是解题的关键.
同课章节目录
