河北省涿州市2019-2020学年八年级上学期期末数学试题( Word版,附答案解析)
文档属性
| 名称 | 河北省涿州市2019-2020学年八年级上学期期末数学试题( Word版,附答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 360.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:00:00 | ||
图片预览



文档简介
河北省涿州市2019-2020学年八年级上学期期末数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下面四个美术字中可以看作轴对称图形的是( )
A. B. C. D.
2.如图,盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,这样做的数学道理是( )
A.两点之间线段最短 B.垂线段最短
C.两点确定一条直线 D.三角形具有稳定性
3.如图,小强利用全等三角形的知识测量池塘两段M、N的距离.如果△PQO≌△NMO,则只需测出其长度的线段是( )
A.线段OP
B.线段OQ
C.线段PQ
D.线段PN
4.若a+b=4,则a2+2ab+b2的值是( )
A.8 B.16 C.2 D.4
5.氢原子中电子和原子核之间的距离为0.00000000529厘米,用科学记数法表示0.00000000529是( )
A.5.29×10-8 B.5.29×10-9 C.5.29×10-10 D.5.29×109
6.因式分解的结果是( )
A.(x+8)(x+1) B.(x+2)(x-4)
C. D.
7.下列分式中,属于最简分式的是( )
A. B. C. D.
8.一个多边形的内角和与它的外角和相等,则这个多边形的边数是( )
A.3 B.4 C.5 D.6
9.能把一个三角形的面积平均分成两个面积相等的三角形,这条线一定是这个三角形的一条( )
A.角平分线 B.高 C.中线 D.一条边的垂直平分线
10.若分式的值为0,则x的值为
A.3 B. C.3或 D.0
11.如图,一定全等的两个三角形是( )
A.①与② B.①与③ C.②与③ D.以上答案都不对
12.如图,把边长为12的等边三角形纸板剪去三个小等边三角形,得到正六边形,则剪去的小等边三角形的边长为( )
A.1 B.2 C.3 D.4
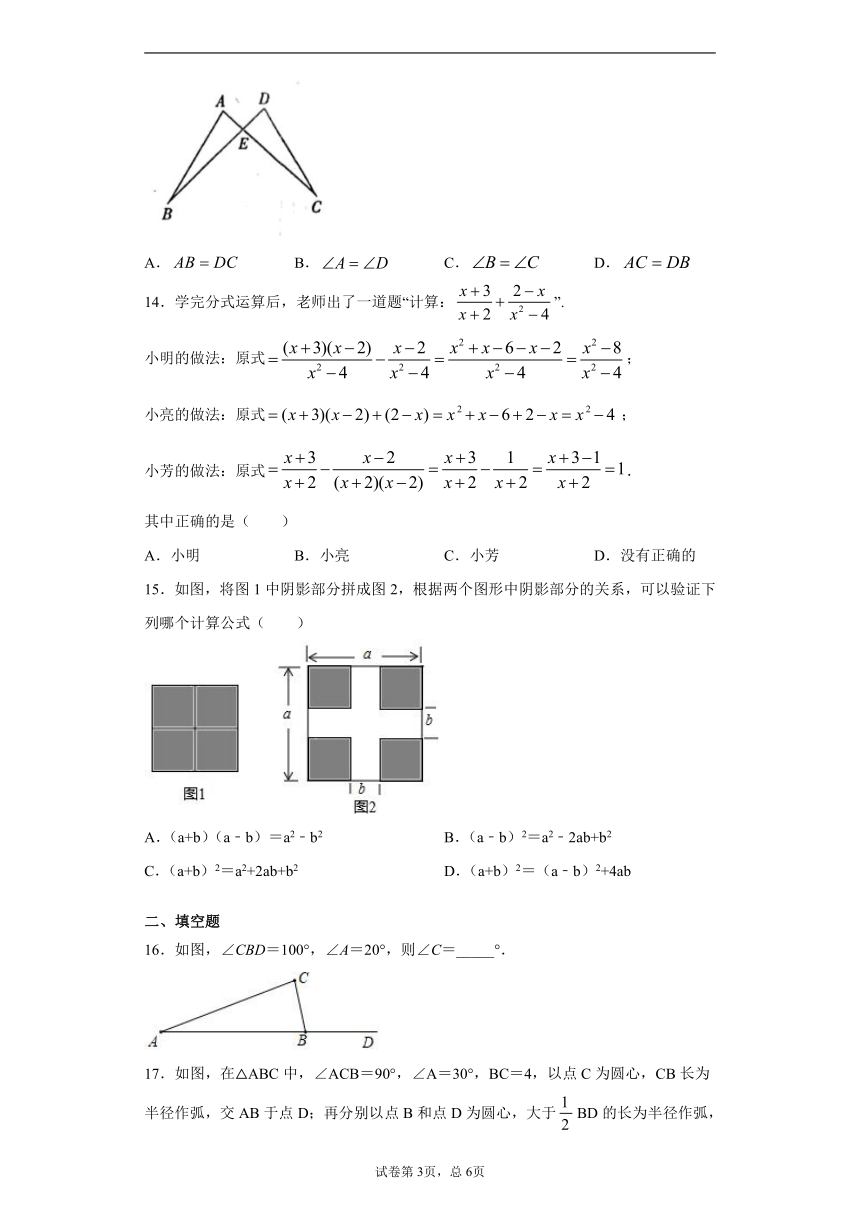
13.如图,与相交于,且,如果添加一个条件还不能判定≌,则添加的这个条件是( )
A. B. C. D.
14.学完分式运算后,老师出了一道题“计算:”.
小明的做法:原式;
小亮的做法:原式;
小芳的做法:原式.
其中正确的是( )
A.小明 B.小亮 C.小芳 D.没有正确的
15.如图,将图1中阴影部分拼成图2,根据两个图形中阴影部分的关系,可以验证下列哪个计算公式( )
A.(a+b)(a﹣b)=a2﹣b2 B.(a﹣b)2=a2﹣2ab+b2
C.(a+b)2=a2+2ab+b2 D.(a+b)2=(a﹣b)2+4ab
二、填空题
16.如图,∠CBD=100°,∠A=20°,则∠C=_____°.
17.如图,在△ABC中,∠ACB=90°,∠A=30°,BC=4,以点C为圆心,CB长为半径作弧,交AB于点D;再分别以点B和点D为圆心,大于BD的长为半径作弧,两弧相交于点E,作射线CE交AB于点F,则AF的长为_____.
18.把x3-6x2+9x分解因式的结果是______________.
19.有两根小棒分别长2厘米和4厘米.要围成一个等腰三角形,第三根小棒的长度应该是____厘米.
20.观察下列各式:
(a﹣b)(a+b)=a2﹣b2
(a﹣b)(a2+ab+b2)=a3﹣b3
(a﹣b)(a3+a2b+ab2+b3)=a4﹣b4
………
这些等式反映出多项式乘法的某种运算规律.当n为正整数,且n≥2时,请你猜想:
(a﹣b)(an﹣1+an﹣2b+an﹣3b2+……+a2bn﹣3+abn﹣2+bn﹣1)=______________.
三、解答题
21.计算:
(1)
(2)
(3)
(4)
22.如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.求证:AB=AC.
23.先化简,然后a在﹣1、0、2、3四个数中选一个合适的数代入求值.
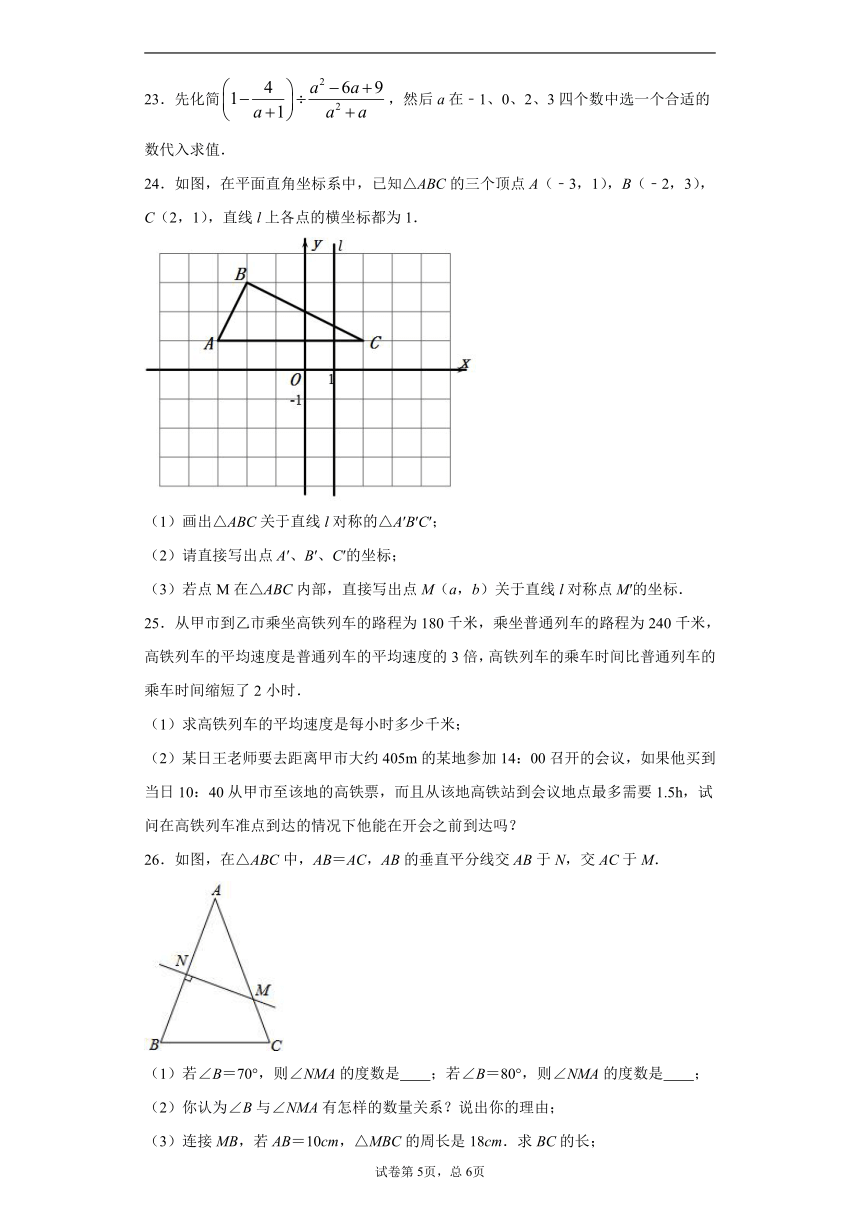
24.如图,在平面直角坐标系中,已知△ABC的三个顶点A(﹣3,1),B(﹣2,3),C(2,1),直线l上各点的横坐标都为1.
(1)画出△ABC关于直线l对称的△A′B′C′;
(2)请直接写出点A′、B′、C′的坐标;
(3)若点M在△ABC内部,直接写出点M(a,b)关于直线l对称点M′的坐标.
25.从甲市到乙市乘坐高铁列车的路程为180千米,乘坐普通列车的路程为240千米,高铁列车的平均速度是普通列车的平均速度的3倍,高铁列车的乘车时间比普通列车的乘车时间缩短了2小时.
(1)求高铁列车的平均速度是每小时多少千米;
(2)某日王老师要去距离甲市大约405m的某地参加14:00召开的会议,如果他买到当日10:40从甲市至该地的高铁票,而且从该地高铁站到会议地点最多需要1.5h,试问在高铁列车准点到达的情况下他能在开会之前到达吗?
26.如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于M.
(1)若∠B=70°,则∠NMA的度数是 ;若∠B=80°,则∠NMA的度数是 ;
(2)你认为∠B与∠NMA有怎样的数量关系?说出你的理由;
(3)连接MB,若AB=10cm,△MBC的周长是18cm.求BC的长;
(4)点Q是BC边上的一个动点,在直线MN上是否存在点P,使PB+PQ的和最小?若存在请标出点P的位置并加以说明;若不存在,请说明理由.
参考答案
1.D
【分析】
根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;据此判断即可.
【详解】
四个汉字中只有“善”字可以看作轴对称图形.
故选D.
【点睛】
本题考查了轴对称图形的知识,掌握轴对称图形的意义,判断是不是轴对称图形的关键是找出对称轴,看图形沿对称轴对折后两部分能否完全重合.
2.D
【分析】
用木条固定矩形门框,即是组成三角形,故可用三角形的稳定性解释.
【详解】
解:加上木条后,原不稳定的四边形中具有了稳定的三角形,故这种做法根据的是三角形的稳定性.
故选D.
【点睛】
本题考查三角形稳定性的实际应用.三角形的稳定性在实际生活中有着广泛的应用..
3.C
【分析】
利用全等三角形对应边相等可知要想求得MN的长,只需求得其对应边PQ的长,据此可以得到答案.
【详解】
解:要想利用△PQO≌△NMO求得MN的长,只需求得线段PQ的长,
故选:C.
【点睛】
本题考查了全等三角形的应用,解题的关键是如何将实际问题与数学知识有机的结合在一起.
4.B
【解析】
试题分析:完全平方公式: a2±2ab+b2= (a±b)2,由题,∵a+b=4,∴a2+2ab+b2=(a+b)2=42=16,故选B.
考点:完全平方公式.
5.B
【分析】
绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10?n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【详解】
解:0.00000000529=5.29×10?9,
故选:B.
【点睛】
本题考查用科学记数法表示较小的数,一般形式为a×10?n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
6.B
【解析】
试题分析:=(x﹣1+3)(x﹣1﹣3)=(x+2)(x﹣4).故选B.
考点:因式分解-运用公式法.
7.D
【分析】
根据最简分式的定义即可判断.
【详解】
解:,故A选项错误;
,故B选项错误;
,故C选项错误;
,故D选项正确.
故选:D
【点睛】
本题主要考查的是最简分式的定义,正确的掌握最简分式的定义是解题的关键.
8.B
【分析】
根据多边形的内角和公式、外角和即可得.
【详解】
设这个多边形的边数是,
因为任意多边形的外角和都等于,
所以,
解得,
即这个多边形的边数是4,
故选:B.
【点睛】
本题考查了多边形的内角和与外角和,熟练掌握多边形的内角和公式是解题关键.
9.C
【分析】
根据中线的性质即可求解.
【详解】
解:三角形的一条中线将三角形的面积平均分成两个面积相等的三角形,
故选:C
【点睛】
本题主要考查的是中线的性质,正确的掌握中线的性质是解题的关键.
10.A
【分析】
根据分式的值为零的条件可以求出x的值.
【详解】
由分式的值为零的条件得x-3=0,且x+3≠0,
解得x=3.
故选A.
【点睛】
本题考查了分式值为0的条件,具备两个条件:(1)分子为0;(2)分母不为0.这两个条件缺一不可.
11.B
【分析】
根据ASA进行判断即可.
【详解】
在三角形①和三角形③中∠B=∠D,BC=DE,∠C=∠E,
∴△ABC≌△FDE(ASA),
故选:B.
【点睛】
本题考查了全等三角形的判定和性质,掌握知识点是解题关键.
12.D
【分析】
由题意可知剪去的三个三角形是全等的等边三角形,由原等边三角形的边长可知得到剪去的小正三角的边长.
【详解】
如图,
∵六边形BCEFHI是正六边形,
∴BC=CE=EF=FH=HI=BC,
∴∠1=∠2=∠3=∠4=∠5=∠6=120°,
∴∠7=∠8=∠9=∠10=∠11=∠12=60°,
∴△ABI≌△DEC≌△GHF,且都是等边三角形,
∴AB=BC=CD=12÷3=4.
?故选D
【点睛】
本题主要考查等边三角形的性质与判定,正六边形的性质,全等三角形的判定与性质,熟练掌握等边三角形的性质与判定定理是解题的关键.
13.A
【分析】
根据题意可得,对顶角相等即,再根据全等三角形的判定定理(SAS,ASA,AAS,SSS)逐个判断即可.
【详解】
A.,它们的夹角是,不是,
∴无法判定≌,故本选项符合.
B.在≌中,
,
∴≌(ASA),故本选项不符合.
C.在≌中,
,
∴≌(AAS),故本选项不符合.
D.,
,
在≌中,
,
∴≌(SAS),故本选项不符合.
故选A.
【点睛】
此题考查全等三角形的判定,解题关键在于掌握全等三角形的判定定理(SAS,ASA,AAS,SSS).
14.C
【解析】
试题解析:
=
=
=
=
=1.
所以正确的应是小芳.
故选C.
15.B
【分析】
根据图形确定出图1与图2中阴影部分的面积,由此即可解答.
【详解】
∵图1中阴影部分的面积为:(a﹣b)2;图2中阴影部分的面积为:a2﹣2ab+b2;
∴(a﹣b)2=a2﹣2ab+b2,
故选B.
【点睛】
本题考查了完全平方公式的几何背景,用不同的方法表示出阴影部分的面积是解题的关键.
16.80
【分析】
根据三角形的外角性质即可得.
【详解】
是的外角,
,
又,
,
故答案为:80.
【点睛】
本题考查了三角形的外角性质,熟练掌握三角形的外角性质是解题关键.
17.6;
【解析】
分析:根据辅助线做法得出CF⊥AB,然后根据含有30°角的直角三角形得出AB和BF的长度,从而得出AF的长度.
详解:∵根据作图法则可得:CF⊥AB, ∵∠ACB=90°,∠A=30°,BC=4,
∴AB=2BC=8, ∵∠CFB=90°,∠B=60°, ∴BF=BC=2,
∴AF=AB-BF=8-2=6.
点睛:本题主要考查的是含有30°角的直角三角形的性质,属于基础题型.解题的关键就是根据作图法则得出直角三角形.
18.x(x﹣3)2
【分析】
先提取公因式,然后按照完全平方公式因式分解即可.
【详解】
解:x3-6x2+9x
=x(x2-6x+9)
=x(x-3)2
故答案为:x(x-3)2.
【点睛】
本题考查了因式分解,掌握知识点是解题关键.
19.4
【分析】
根据三角形三边关系:三角形的任意两边之和大于第三边,任意两边之差小于第三边即可得出结果.
【详解】
解:∵要围成一个等腰三角形,
∴有两种可能:2、2、4和2、4、4,
2+2=4,所以2、2、4舍掉,
∴第三根小棒的长度为4,
故答案为:4
【点睛】
本题主要考查的三角形三边关系,掌握三角形的三边关系是解题的关键.
20.an﹣bn
【分析】
根据所给信息,可知各个等式的左边两因式中,一项为(a-b),另一项每一项的次数均为n-1,而且按照字母a的降幂排列,故可得答案.
【详解】
解:由题意,当n=1时,有(a﹣b)(a+b)=a2﹣b2;当n=2时,有(a﹣b)(a2+ab+b2)=a3﹣b3;当n=3时,有(a﹣b)(a3+a2b+ab2+b3)=a4﹣b4;所以得到(a﹣b)(an﹣1+an﹣2b+an﹣3b2+……+a2bn﹣3+abn﹣2+bn﹣1)=an﹣bn.
故答案为:an﹣bn.
【点睛】
本题的考点是归纳推理,主要考查信息的处理,关键是根据所给信息,可知两因式中,一项为(a-b),另一项每一项的次数均为n-1,而且按照字母a的降幂排列.
21.(1)﹣1;(2)7ab﹣2a2;(3) ;(4)
【分析】
(1)按照零指数幂和负指数幂法则计算,再求和即可;
(2)用括号内各项分别和相除即可;
(3)先进行乘方运算,再用乘法分配律计算;
(4)分别进行多项式乘法和运用完全平方公式,再合并同类项即可.
【详解】
解:(1);
(2);
(3);
(4).
【点睛】
本题考查了零指数幂、负指数幂和整式的乘除法运算,解答关键是按照相关法则进行计算.
22.证明见解析.
【分析】
已知AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,由角平分线的性质定理可得DE=DF,再利用HL证明Rt△BDE≌Rt△CDF,即可得∠B=∠C,由等腰三角形的判定定理即可证得AB=AC.
【详解】
∵AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,
∴DE=DF,
∵BD=CD,
∴Rt△BDE≌Rt△CDF,
∴∠B=∠C,
∴AB=AC.
【点睛】
本题主要考查了角平分线上的点到角两边的距离相等、全等三角形的判定及性质、等腰三角形的判定,比较综合,难度适中.
23.,-2
【分析】
先根据分式混合运算的法则把原式进行化简,再选取合适的a的值代入进行计算即可.
【详解】
解:
=
=
=
当a=2时,原式各分母均有意义,所以a取2,
把a=2代入,原式= -2.
【点睛】
本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.
24.(1)详见解析;(2)A′(5,1)、B′(4,3)、C′(0,1);(3)(﹣a+2,b)
【分析】
(1)利用网格图的特点及轴对称的性质,分别确定A、B、C关于直线l的对称点A′、B′、C′,然后依次连接即可;
(2)直接利用网格图即可在坐标系中确定点A′、B′、C′的坐标;
(3)比较点A、B、C和点A′、B′、C′的坐标规律即可得出M′的坐标.
【详解】
解:(1)如图:△A′B′C′即为所求,
(2)A′(5,1)、B′(4,3)、C′(0,1);
(3)M′的坐标(﹣a+2,b).
【点睛】
此题主要考查轴对称的性质,正确理解关于轴对称的点的坐标特点是解题关键.
25.(1)270(2)他能在开会之前到达
【分析】
(1)设普通列车平均速度每小时x千米,则高速列车平均速度每小时3x千米,根据题意可得,坐高铁走180千米比坐普通车240千米少用2小时,据此列方程求解;
(2)求出王老师所用的时间,然后进行判断.
【详解】
(1)设普通列车平均速度每小时x千米,则高速列车平均速度每小时3x千米,
根据题意得,=2,
解得:x=90,
经检验,x=90是所列方程的根,
则3x=3×90=270.
答:高速列车平均速度为每小时270千米;
(2)405÷270=1.5,
则坐车共需要1.5+1.5=3(小时),
王老师到达会议地点的时间为13点40.
故他能在开会之前到达.
【点睛】
本题考查了分式方程的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程求解,注意检验.
26.(1)50°;70°;(2)∠NMA=2∠B﹣90°,详见解析;(3)8cm;(4)存在,详见解析
【分析】
(1)根据等腰三角的性质,三角形的内角和定理,可得∠A的度数,根据直角三角形两锐角的关系,可得答案;
(2)与(1)的方法相同,先求出∠A,然后根据直角三角形两锐角的关系,可得答案;
(3)根据MN垂直平分AB,可得MB=MA, 根据△MBC的周长是18cm, 即可求出答案;
(4)过点A做AQ⊥BC于Q,与直线MN相交于于点P,连接PB根据MN垂直平分AB,可得PA=PB,又点A到BC的最短距离就是AQ,即可得出结论.
【详解】
解:(1)①∵AB=AC,
∴∠B=∠C,
∴∠A=180°?2∠B,
又∵MN垂直平分AB,
∴∠NMA=90°?∠A=90°?(180°?2∠B)=2∠B?90°=50°;
②∵AB=AC,
∴∠B=∠C,
∴∠A=180°?2∠B,
又∵MN垂直平分AB,
∴∠NMA=90°?∠A=90°?(180°?2∠B)=2∠B?90°=70°
故答案为: 50°;70°;
(2)猜想的结论为:∠NMA=2∠B﹣90°.
理由:∵AB=AC,
∴∠B=∠C,
∴∠A=180°﹣2∠B
又∵MN垂直平分AB,
∴∠NMA=90°﹣∠A=90°﹣(180°﹣2∠B)
=2∠B﹣90°;
(3)如图1:
∵MN垂直平分AB.
∴MB=MA,
又∵△MBC的周长是18cm,
∴AC+BC=18cm,
∵AB=10cm
∴BC=8cm;
(4)存在,如图2,过点A做AQ⊥BC于Q,与直线MN相交于于点P,点P即为所求.
理由:连接PB,∵MN垂直平分AB,
∴PA=PB,又点A到BC的最短距离就是AQ,而AQ=PB+PQ,
∴此时PB+PQ的和最小.
【点睛】
本题考查了轴对称,线段垂直平分线上的点到线段两端点的距离相等,最短距离问题,掌握这些知识点是解题关键.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下面四个美术字中可以看作轴对称图形的是( )
A. B. C. D.
2.如图,盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,这样做的数学道理是( )
A.两点之间线段最短 B.垂线段最短
C.两点确定一条直线 D.三角形具有稳定性
3.如图,小强利用全等三角形的知识测量池塘两段M、N的距离.如果△PQO≌△NMO,则只需测出其长度的线段是( )
A.线段OP
B.线段OQ
C.线段PQ
D.线段PN
4.若a+b=4,则a2+2ab+b2的值是( )
A.8 B.16 C.2 D.4
5.氢原子中电子和原子核之间的距离为0.00000000529厘米,用科学记数法表示0.00000000529是( )
A.5.29×10-8 B.5.29×10-9 C.5.29×10-10 D.5.29×109
6.因式分解的结果是( )
A.(x+8)(x+1) B.(x+2)(x-4)
C. D.
7.下列分式中,属于最简分式的是( )
A. B. C. D.
8.一个多边形的内角和与它的外角和相等,则这个多边形的边数是( )
A.3 B.4 C.5 D.6
9.能把一个三角形的面积平均分成两个面积相等的三角形,这条线一定是这个三角形的一条( )
A.角平分线 B.高 C.中线 D.一条边的垂直平分线
10.若分式的值为0,则x的值为
A.3 B. C.3或 D.0
11.如图,一定全等的两个三角形是( )
A.①与② B.①与③ C.②与③ D.以上答案都不对
12.如图,把边长为12的等边三角形纸板剪去三个小等边三角形,得到正六边形,则剪去的小等边三角形的边长为( )
A.1 B.2 C.3 D.4
13.如图,与相交于,且,如果添加一个条件还不能判定≌,则添加的这个条件是( )
A. B. C. D.
14.学完分式运算后,老师出了一道题“计算:”.
小明的做法:原式;
小亮的做法:原式;
小芳的做法:原式.
其中正确的是( )
A.小明 B.小亮 C.小芳 D.没有正确的
15.如图,将图1中阴影部分拼成图2,根据两个图形中阴影部分的关系,可以验证下列哪个计算公式( )
A.(a+b)(a﹣b)=a2﹣b2 B.(a﹣b)2=a2﹣2ab+b2
C.(a+b)2=a2+2ab+b2 D.(a+b)2=(a﹣b)2+4ab
二、填空题
16.如图,∠CBD=100°,∠A=20°,则∠C=_____°.
17.如图,在△ABC中,∠ACB=90°,∠A=30°,BC=4,以点C为圆心,CB长为半径作弧,交AB于点D;再分别以点B和点D为圆心,大于BD的长为半径作弧,两弧相交于点E,作射线CE交AB于点F,则AF的长为_____.
18.把x3-6x2+9x分解因式的结果是______________.
19.有两根小棒分别长2厘米和4厘米.要围成一个等腰三角形,第三根小棒的长度应该是____厘米.
20.观察下列各式:
(a﹣b)(a+b)=a2﹣b2
(a﹣b)(a2+ab+b2)=a3﹣b3
(a﹣b)(a3+a2b+ab2+b3)=a4﹣b4
………
这些等式反映出多项式乘法的某种运算规律.当n为正整数,且n≥2时,请你猜想:
(a﹣b)(an﹣1+an﹣2b+an﹣3b2+……+a2bn﹣3+abn﹣2+bn﹣1)=______________.
三、解答题
21.计算:
(1)
(2)
(3)
(4)
22.如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.求证:AB=AC.
23.先化简,然后a在﹣1、0、2、3四个数中选一个合适的数代入求值.
24.如图,在平面直角坐标系中,已知△ABC的三个顶点A(﹣3,1),B(﹣2,3),C(2,1),直线l上各点的横坐标都为1.
(1)画出△ABC关于直线l对称的△A′B′C′;
(2)请直接写出点A′、B′、C′的坐标;
(3)若点M在△ABC内部,直接写出点M(a,b)关于直线l对称点M′的坐标.
25.从甲市到乙市乘坐高铁列车的路程为180千米,乘坐普通列车的路程为240千米,高铁列车的平均速度是普通列车的平均速度的3倍,高铁列车的乘车时间比普通列车的乘车时间缩短了2小时.
(1)求高铁列车的平均速度是每小时多少千米;
(2)某日王老师要去距离甲市大约405m的某地参加14:00召开的会议,如果他买到当日10:40从甲市至该地的高铁票,而且从该地高铁站到会议地点最多需要1.5h,试问在高铁列车准点到达的情况下他能在开会之前到达吗?
26.如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于M.
(1)若∠B=70°,则∠NMA的度数是 ;若∠B=80°,则∠NMA的度数是 ;
(2)你认为∠B与∠NMA有怎样的数量关系?说出你的理由;
(3)连接MB,若AB=10cm,△MBC的周长是18cm.求BC的长;
(4)点Q是BC边上的一个动点,在直线MN上是否存在点P,使PB+PQ的和最小?若存在请标出点P的位置并加以说明;若不存在,请说明理由.
参考答案
1.D
【分析】
根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;据此判断即可.
【详解】
四个汉字中只有“善”字可以看作轴对称图形.
故选D.
【点睛】
本题考查了轴对称图形的知识,掌握轴对称图形的意义,判断是不是轴对称图形的关键是找出对称轴,看图形沿对称轴对折后两部分能否完全重合.
2.D
【分析】
用木条固定矩形门框,即是组成三角形,故可用三角形的稳定性解释.
【详解】
解:加上木条后,原不稳定的四边形中具有了稳定的三角形,故这种做法根据的是三角形的稳定性.
故选D.
【点睛】
本题考查三角形稳定性的实际应用.三角形的稳定性在实际生活中有着广泛的应用..
3.C
【分析】
利用全等三角形对应边相等可知要想求得MN的长,只需求得其对应边PQ的长,据此可以得到答案.
【详解】
解:要想利用△PQO≌△NMO求得MN的长,只需求得线段PQ的长,
故选:C.
【点睛】
本题考查了全等三角形的应用,解题的关键是如何将实际问题与数学知识有机的结合在一起.
4.B
【解析】
试题分析:完全平方公式: a2±2ab+b2= (a±b)2,由题,∵a+b=4,∴a2+2ab+b2=(a+b)2=42=16,故选B.
考点:完全平方公式.
5.B
【分析】
绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10?n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
【详解】
解:0.00000000529=5.29×10?9,
故选:B.
【点睛】
本题考查用科学记数法表示较小的数,一般形式为a×10?n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
6.B
【解析】
试题分析:=(x﹣1+3)(x﹣1﹣3)=(x+2)(x﹣4).故选B.
考点:因式分解-运用公式法.
7.D
【分析】
根据最简分式的定义即可判断.
【详解】
解:,故A选项错误;
,故B选项错误;
,故C选项错误;
,故D选项正确.
故选:D
【点睛】
本题主要考查的是最简分式的定义,正确的掌握最简分式的定义是解题的关键.
8.B
【分析】
根据多边形的内角和公式、外角和即可得.
【详解】
设这个多边形的边数是,
因为任意多边形的外角和都等于,
所以,
解得,
即这个多边形的边数是4,
故选:B.
【点睛】
本题考查了多边形的内角和与外角和,熟练掌握多边形的内角和公式是解题关键.
9.C
【分析】
根据中线的性质即可求解.
【详解】
解:三角形的一条中线将三角形的面积平均分成两个面积相等的三角形,
故选:C
【点睛】
本题主要考查的是中线的性质,正确的掌握中线的性质是解题的关键.
10.A
【分析】
根据分式的值为零的条件可以求出x的值.
【详解】
由分式的值为零的条件得x-3=0,且x+3≠0,
解得x=3.
故选A.
【点睛】
本题考查了分式值为0的条件,具备两个条件:(1)分子为0;(2)分母不为0.这两个条件缺一不可.
11.B
【分析】
根据ASA进行判断即可.
【详解】
在三角形①和三角形③中∠B=∠D,BC=DE,∠C=∠E,
∴△ABC≌△FDE(ASA),
故选:B.
【点睛】
本题考查了全等三角形的判定和性质,掌握知识点是解题关键.
12.D
【分析】
由题意可知剪去的三个三角形是全等的等边三角形,由原等边三角形的边长可知得到剪去的小正三角的边长.
【详解】
如图,
∵六边形BCEFHI是正六边形,
∴BC=CE=EF=FH=HI=BC,
∴∠1=∠2=∠3=∠4=∠5=∠6=120°,
∴∠7=∠8=∠9=∠10=∠11=∠12=60°,
∴△ABI≌△DEC≌△GHF,且都是等边三角形,
∴AB=BC=CD=12÷3=4.
?故选D
【点睛】
本题主要考查等边三角形的性质与判定,正六边形的性质,全等三角形的判定与性质,熟练掌握等边三角形的性质与判定定理是解题的关键.
13.A
【分析】
根据题意可得,对顶角相等即,再根据全等三角形的判定定理(SAS,ASA,AAS,SSS)逐个判断即可.
【详解】
A.,它们的夹角是,不是,
∴无法判定≌,故本选项符合.
B.在≌中,
,
∴≌(ASA),故本选项不符合.
C.在≌中,
,
∴≌(AAS),故本选项不符合.
D.,
,
在≌中,
,
∴≌(SAS),故本选项不符合.
故选A.
【点睛】
此题考查全等三角形的判定,解题关键在于掌握全等三角形的判定定理(SAS,ASA,AAS,SSS).
14.C
【解析】
试题解析:
=
=
=
=
=1.
所以正确的应是小芳.
故选C.
15.B
【分析】
根据图形确定出图1与图2中阴影部分的面积,由此即可解答.
【详解】
∵图1中阴影部分的面积为:(a﹣b)2;图2中阴影部分的面积为:a2﹣2ab+b2;
∴(a﹣b)2=a2﹣2ab+b2,
故选B.
【点睛】
本题考查了完全平方公式的几何背景,用不同的方法表示出阴影部分的面积是解题的关键.
16.80
【分析】
根据三角形的外角性质即可得.
【详解】
是的外角,
,
又,
,
故答案为:80.
【点睛】
本题考查了三角形的外角性质,熟练掌握三角形的外角性质是解题关键.
17.6;
【解析】
分析:根据辅助线做法得出CF⊥AB,然后根据含有30°角的直角三角形得出AB和BF的长度,从而得出AF的长度.
详解:∵根据作图法则可得:CF⊥AB, ∵∠ACB=90°,∠A=30°,BC=4,
∴AB=2BC=8, ∵∠CFB=90°,∠B=60°, ∴BF=BC=2,
∴AF=AB-BF=8-2=6.
点睛:本题主要考查的是含有30°角的直角三角形的性质,属于基础题型.解题的关键就是根据作图法则得出直角三角形.
18.x(x﹣3)2
【分析】
先提取公因式,然后按照完全平方公式因式分解即可.
【详解】
解:x3-6x2+9x
=x(x2-6x+9)
=x(x-3)2
故答案为:x(x-3)2.
【点睛】
本题考查了因式分解,掌握知识点是解题关键.
19.4
【分析】
根据三角形三边关系:三角形的任意两边之和大于第三边,任意两边之差小于第三边即可得出结果.
【详解】
解:∵要围成一个等腰三角形,
∴有两种可能:2、2、4和2、4、4,
2+2=4,所以2、2、4舍掉,
∴第三根小棒的长度为4,
故答案为:4
【点睛】
本题主要考查的三角形三边关系,掌握三角形的三边关系是解题的关键.
20.an﹣bn
【分析】
根据所给信息,可知各个等式的左边两因式中,一项为(a-b),另一项每一项的次数均为n-1,而且按照字母a的降幂排列,故可得答案.
【详解】
解:由题意,当n=1时,有(a﹣b)(a+b)=a2﹣b2;当n=2时,有(a﹣b)(a2+ab+b2)=a3﹣b3;当n=3时,有(a﹣b)(a3+a2b+ab2+b3)=a4﹣b4;所以得到(a﹣b)(an﹣1+an﹣2b+an﹣3b2+……+a2bn﹣3+abn﹣2+bn﹣1)=an﹣bn.
故答案为:an﹣bn.
【点睛】
本题的考点是归纳推理,主要考查信息的处理,关键是根据所给信息,可知两因式中,一项为(a-b),另一项每一项的次数均为n-1,而且按照字母a的降幂排列.
21.(1)﹣1;(2)7ab﹣2a2;(3) ;(4)
【分析】
(1)按照零指数幂和负指数幂法则计算,再求和即可;
(2)用括号内各项分别和相除即可;
(3)先进行乘方运算,再用乘法分配律计算;
(4)分别进行多项式乘法和运用完全平方公式,再合并同类项即可.
【详解】
解:(1);
(2);
(3);
(4).
【点睛】
本题考查了零指数幂、负指数幂和整式的乘除法运算,解答关键是按照相关法则进行计算.
22.证明见解析.
【分析】
已知AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,由角平分线的性质定理可得DE=DF,再利用HL证明Rt△BDE≌Rt△CDF,即可得∠B=∠C,由等腰三角形的判定定理即可证得AB=AC.
【详解】
∵AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,
∴DE=DF,
∵BD=CD,
∴Rt△BDE≌Rt△CDF,
∴∠B=∠C,
∴AB=AC.
【点睛】
本题主要考查了角平分线上的点到角两边的距离相等、全等三角形的判定及性质、等腰三角形的判定,比较综合,难度适中.
23.,-2
【分析】
先根据分式混合运算的法则把原式进行化简,再选取合适的a的值代入进行计算即可.
【详解】
解:
=
=
=
当a=2时,原式各分母均有意义,所以a取2,
把a=2代入,原式= -2.
【点睛】
本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.
24.(1)详见解析;(2)A′(5,1)、B′(4,3)、C′(0,1);(3)(﹣a+2,b)
【分析】
(1)利用网格图的特点及轴对称的性质,分别确定A、B、C关于直线l的对称点A′、B′、C′,然后依次连接即可;
(2)直接利用网格图即可在坐标系中确定点A′、B′、C′的坐标;
(3)比较点A、B、C和点A′、B′、C′的坐标规律即可得出M′的坐标.
【详解】
解:(1)如图:△A′B′C′即为所求,
(2)A′(5,1)、B′(4,3)、C′(0,1);
(3)M′的坐标(﹣a+2,b).
【点睛】
此题主要考查轴对称的性质,正确理解关于轴对称的点的坐标特点是解题关键.
25.(1)270(2)他能在开会之前到达
【分析】
(1)设普通列车平均速度每小时x千米,则高速列车平均速度每小时3x千米,根据题意可得,坐高铁走180千米比坐普通车240千米少用2小时,据此列方程求解;
(2)求出王老师所用的时间,然后进行判断.
【详解】
(1)设普通列车平均速度每小时x千米,则高速列车平均速度每小时3x千米,
根据题意得,=2,
解得:x=90,
经检验,x=90是所列方程的根,
则3x=3×90=270.
答:高速列车平均速度为每小时270千米;
(2)405÷270=1.5,
则坐车共需要1.5+1.5=3(小时),
王老师到达会议地点的时间为13点40.
故他能在开会之前到达.
【点睛】
本题考查了分式方程的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程求解,注意检验.
26.(1)50°;70°;(2)∠NMA=2∠B﹣90°,详见解析;(3)8cm;(4)存在,详见解析
【分析】
(1)根据等腰三角的性质,三角形的内角和定理,可得∠A的度数,根据直角三角形两锐角的关系,可得答案;
(2)与(1)的方法相同,先求出∠A,然后根据直角三角形两锐角的关系,可得答案;
(3)根据MN垂直平分AB,可得MB=MA, 根据△MBC的周长是18cm, 即可求出答案;
(4)过点A做AQ⊥BC于Q,与直线MN相交于于点P,连接PB根据MN垂直平分AB,可得PA=PB,又点A到BC的最短距离就是AQ,即可得出结论.
【详解】
解:(1)①∵AB=AC,
∴∠B=∠C,
∴∠A=180°?2∠B,
又∵MN垂直平分AB,
∴∠NMA=90°?∠A=90°?(180°?2∠B)=2∠B?90°=50°;
②∵AB=AC,
∴∠B=∠C,
∴∠A=180°?2∠B,
又∵MN垂直平分AB,
∴∠NMA=90°?∠A=90°?(180°?2∠B)=2∠B?90°=70°
故答案为: 50°;70°;
(2)猜想的结论为:∠NMA=2∠B﹣90°.
理由:∵AB=AC,
∴∠B=∠C,
∴∠A=180°﹣2∠B
又∵MN垂直平分AB,
∴∠NMA=90°﹣∠A=90°﹣(180°﹣2∠B)
=2∠B﹣90°;
(3)如图1:
∵MN垂直平分AB.
∴MB=MA,
又∵△MBC的周长是18cm,
∴AC+BC=18cm,
∵AB=10cm
∴BC=8cm;
(4)存在,如图2,过点A做AQ⊥BC于Q,与直线MN相交于于点P,点P即为所求.
理由:连接PB,∵MN垂直平分AB,
∴PA=PB,又点A到BC的最短距离就是AQ,而AQ=PB+PQ,
∴此时PB+PQ的和最小.
【点睛】
本题考查了轴对称,线段垂直平分线上的点到线段两端点的距离相等,最短距离问题,掌握这些知识点是解题关键.
同课章节目录
