1.3 有理数的大小 课件(共20张PPT)
文档属性
| 名称 | 1.3 有理数的大小 课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 583.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:00:00 | ||
图片预览





文档简介
1.3 有理数的大小
第1章 有理数
学习目标
1.掌握有理数大小的比较法则;
2.能利用数轴及绝对值的知识,比较两个有理数的
大小.(重点、难点)
导入新课
下图表示某一天我国5个城市的最低气温.
武汉5 ℃ 北京-10℃ 上海0℃ 广州10℃ 哈尔滨-20℃
问题:你能将上述五个城市的最低气温按从低到高的顺序依次排列吗?
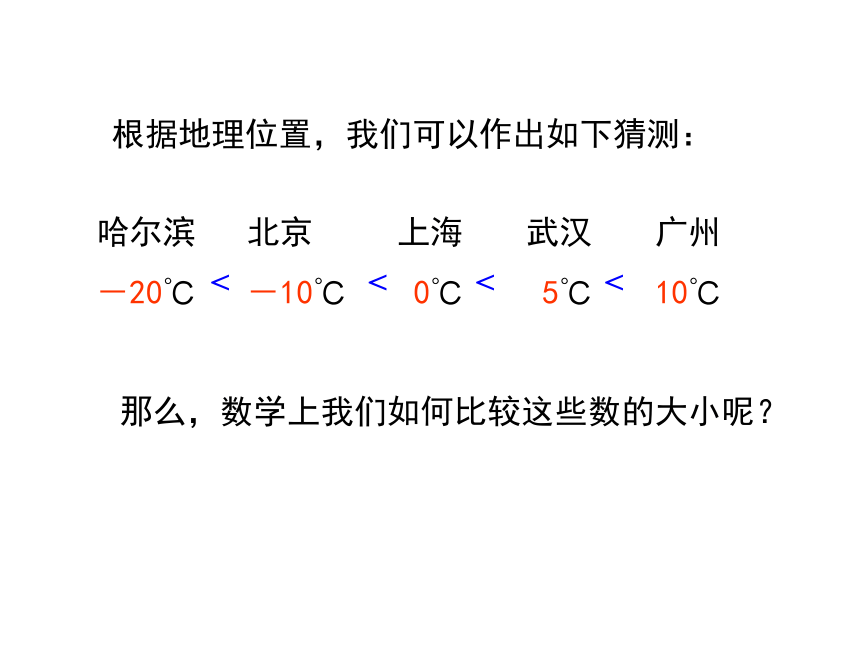
哈尔滨
-20℃
北京
-10℃
上海
0℃
武汉
5℃
广州
10℃
<
<
<
<
根据地理位置,我们可以作出如下猜测:
那么,数学上我们如何比较这些数的大小呢?
讲授新课
借助数轴比较有理数的大小
一
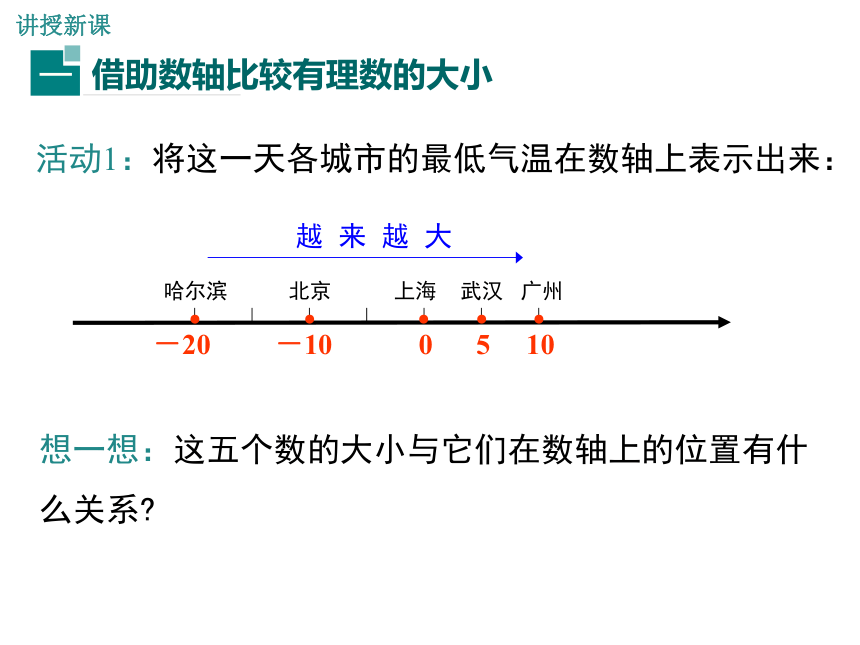
活动1:将这一天各城市的最低气温在数轴上表示出来:
-20 -10 0 5 10
●
●
●
●
●
武汉
上海
北京
哈尔滨
广州
想一想:这五个数的大小与它们在数轴上的位置有什么关系?
越 来 越 大
高+
低-
原点
-3 –2 –1 0 1 2 3
右边
大
左边
小
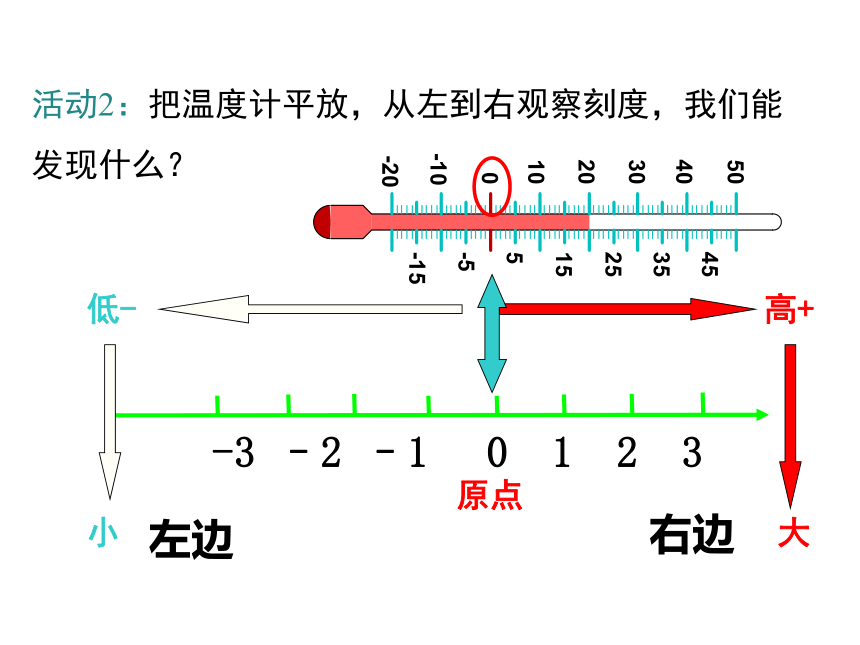
活动2:把温度计平放,从左到右观察刻度,我们能发现什么?
活动3:类比倒置的温度计,观察数轴上两个点表示的数,右边的与左边有怎样的大小关系?你发现了什么?
越来越大
结论:
(1)数轴上两个点表示的数,右边的总比左边的大.
(2)正数大于0,负数小于0,正数大于负数.
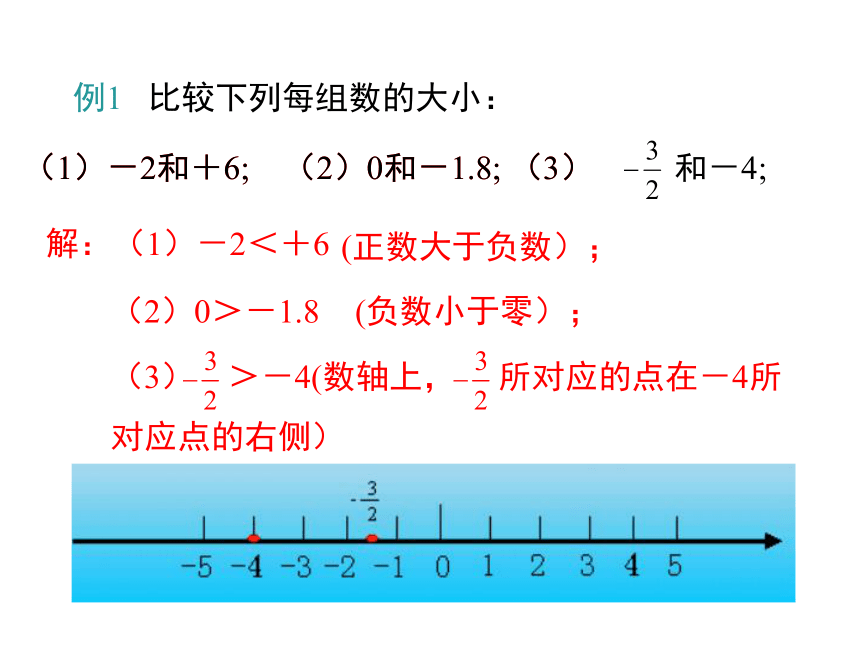
例1 比较下列每组数的大小:
(1)-2和+6; (2)0和-1.8; (3)
解:(1)-2<+6
(正数大于负数);
(2)0>-1.8
(负数小于零);
(1)-2和+6; (2)0和-1.8; (3)
和-4;
(3) >-4(数轴上, 所对应的点在-4所对应点的右侧)
例2 m,n两个有理数在数轴上的对应点如图所示,下列结论中正确的是( )
A.n>m B.-m>|n|
C.-n>|m| D.|n|<|m|
解析:首先根据n、m的位置可得n<0,m>0,再在数轴上标出n、m的相反数-n、-m,进而得-m<0,-n>0,然后再根据数轴比较大小即可.
D
练一练:在数轴上把下列各数表示出来,并比较
它们的大小: ,7,-3.5,0, .
1
0
2
3
4
5
6
7
-1
-2
-3
8
7
-3.5
0
解:如图所示.
由图可知,它们大小关系为
-3.5 < < 0 < < 7
有最小的有理数吗?有最大的有理数吗?结合数轴说说.
(1)0是最小的有理数.( )
(2)-1是最大的负整数( )
╳
√
-3 –2–1 0 1 2 3 4
议一议
练一练:设a是绝对值最小的数,b是最大的负整数,c是最小的正整数,则a、b、c三数分别为( )
A.0,-1,1 B.1,0,-1
C.1,-1,0 D.0,1,-1
A
运用绝对值比较有理数的大小
二
做一做:在数轴上分别表示下列各对数,比较它们的大小:
(1)-1与-3; (2)-5与-2.
-5 -4 -3 -2 -1 0 1 2 3 4 5
(1)-3<-1; (2)-5<-2.
解:
两个负数,绝对值大的反而小.
试一试:求出各对数的绝对值,并比较它们的大小.
|-1|=1;|-3|=3;
|-1|<|-3|
|-2|=2;
|-5|=5;
|-2|<|-5|
-5<-2
-3<-1
对比
观察
结论
解:
(1)因为|-2|=2;|-3|=3,2<3,所以-2>-3.
(2)因为 = =0.6;|0.8|=0.8,0.6<0.8,
所以 > -0.8.
例3 比较下列每组数的大小:
(1)-2与-3;
(2) 与-0.8;
比较有理数的大小时,应抓住两点:
1.识别数的正负性,直接利用“正数>0>负数”进行比较;
2.两个负数相比较,先比较其绝对值,再根据绝对值大的反而小的原则进行比较;
【注意】带有括号或是绝对值的两个数进行大小比较,需先化简,再比较大小.
最后的结果一定要是原来两数的大小关系.
归纳总结
当堂练习
1. 下表记录了今年一月某日部分城市的最高气温:
城市
阜阳
安庆
淮北
合肥
芜湖
最高气温/℃
-5
2
-3
-1
4
(1)在数轴上表示这些城市最高气温的值;
(2)用“<”连接这些城市的最高气温.
解:(1)如图
(2)-5℃<-3℃<-1℃<2℃<4℃.
2.将下列这些数按从小到大的顺序排列,并用<连接.
0,-3,|5|,-(-4),-|-5|.
-|-5|< -3 <0< -(-4)<|5|.
解:
3.比较下面各对数的大小:
⑴ ____ ; ⑵-3 ____+1;
⑶ -1 ____0; ⑷ - ___- ;
⑸ -|-3| ____-4.5
<
>
<
<
>
(1) 先化简,得
-(-3)=3,
-(+2)=-2,
因为正数大于负数,
所以3>-2,
即-(-3)>-(+2)
解:
(2)先化简,得
4.比较下列每组数的大小
(1)-(-3)和-(+2);
(2)| |和-(-0.83);
有理数的大小比较
求绝对值比较有理数的大小
用数轴比较有理数的大小
步骤:画数轴,找点,排列,不等号连接.
正数大于0,0大于负数,正数大于负数.
步骤:求绝对值,比较绝对值,比较负数的大小.
两个负数比较大小,绝对值大的反而小.
课堂小结
第1章 有理数
学习目标
1.掌握有理数大小的比较法则;
2.能利用数轴及绝对值的知识,比较两个有理数的
大小.(重点、难点)
导入新课
下图表示某一天我国5个城市的最低气温.
武汉5 ℃ 北京-10℃ 上海0℃ 广州10℃ 哈尔滨-20℃
问题:你能将上述五个城市的最低气温按从低到高的顺序依次排列吗?
哈尔滨
-20℃
北京
-10℃
上海
0℃
武汉
5℃
广州
10℃
<
<
<
<
根据地理位置,我们可以作出如下猜测:
那么,数学上我们如何比较这些数的大小呢?
讲授新课
借助数轴比较有理数的大小
一
活动1:将这一天各城市的最低气温在数轴上表示出来:
-20 -10 0 5 10
●
●
●
●
●
武汉
上海
北京
哈尔滨
广州
想一想:这五个数的大小与它们在数轴上的位置有什么关系?
越 来 越 大
高+
低-
原点
-3 –2 –1 0 1 2 3
右边
大
左边
小
活动2:把温度计平放,从左到右观察刻度,我们能发现什么?
活动3:类比倒置的温度计,观察数轴上两个点表示的数,右边的与左边有怎样的大小关系?你发现了什么?
越来越大
结论:
(1)数轴上两个点表示的数,右边的总比左边的大.
(2)正数大于0,负数小于0,正数大于负数.
例1 比较下列每组数的大小:
(1)-2和+6; (2)0和-1.8; (3)
解:(1)-2<+6
(正数大于负数);
(2)0>-1.8
(负数小于零);
(1)-2和+6; (2)0和-1.8; (3)
和-4;
(3) >-4(数轴上, 所对应的点在-4所对应点的右侧)
例2 m,n两个有理数在数轴上的对应点如图所示,下列结论中正确的是( )
A.n>m B.-m>|n|
C.-n>|m| D.|n|<|m|
解析:首先根据n、m的位置可得n<0,m>0,再在数轴上标出n、m的相反数-n、-m,进而得-m<0,-n>0,然后再根据数轴比较大小即可.
D
练一练:在数轴上把下列各数表示出来,并比较
它们的大小: ,7,-3.5,0, .
1
0
2
3
4
5
6
7
-1
-2
-3
8
7
-3.5
0
解:如图所示.
由图可知,它们大小关系为
-3.5 < < 0 < < 7
有最小的有理数吗?有最大的有理数吗?结合数轴说说.
(1)0是最小的有理数.( )
(2)-1是最大的负整数( )
╳
√
-3 –2–1 0 1 2 3 4
议一议
练一练:设a是绝对值最小的数,b是最大的负整数,c是最小的正整数,则a、b、c三数分别为( )
A.0,-1,1 B.1,0,-1
C.1,-1,0 D.0,1,-1
A
运用绝对值比较有理数的大小
二
做一做:在数轴上分别表示下列各对数,比较它们的大小:
(1)-1与-3; (2)-5与-2.
-5 -4 -3 -2 -1 0 1 2 3 4 5
(1)-3<-1; (2)-5<-2.
解:
两个负数,绝对值大的反而小.
试一试:求出各对数的绝对值,并比较它们的大小.
|-1|=1;|-3|=3;
|-1|<|-3|
|-2|=2;
|-5|=5;
|-2|<|-5|
-5<-2
-3<-1
对比
观察
结论
解:
(1)因为|-2|=2;|-3|=3,2<3,所以-2>-3.
(2)因为 = =0.6;|0.8|=0.8,0.6<0.8,
所以 > -0.8.
例3 比较下列每组数的大小:
(1)-2与-3;
(2) 与-0.8;
比较有理数的大小时,应抓住两点:
1.识别数的正负性,直接利用“正数>0>负数”进行比较;
2.两个负数相比较,先比较其绝对值,再根据绝对值大的反而小的原则进行比较;
【注意】带有括号或是绝对值的两个数进行大小比较,需先化简,再比较大小.
最后的结果一定要是原来两数的大小关系.
归纳总结
当堂练习
1. 下表记录了今年一月某日部分城市的最高气温:
城市
阜阳
安庆
淮北
合肥
芜湖
最高气温/℃
-5
2
-3
-1
4
(1)在数轴上表示这些城市最高气温的值;
(2)用“<”连接这些城市的最高气温.
解:(1)如图
(2)-5℃<-3℃<-1℃<2℃<4℃.
2.将下列这些数按从小到大的顺序排列,并用<连接.
0,-3,|5|,-(-4),-|-5|.
-|-5|< -3 <0< -(-4)<|5|.
解:
3.比较下面各对数的大小:
⑴ ____ ; ⑵-3 ____+1;
⑶ -1 ____0; ⑷ - ___- ;
⑸ -|-3| ____-4.5
<
>
<
<
>
(1) 先化简,得
-(-3)=3,
-(+2)=-2,
因为正数大于负数,
所以3>-2,
即-(-3)>-(+2)
解:
(2)先化简,得
4.比较下列每组数的大小
(1)-(-3)和-(+2);
(2)| |和-(-0.83);
有理数的大小比较
求绝对值比较有理数的大小
用数轴比较有理数的大小
步骤:画数轴,找点,排列,不等号连接.
正数大于0,0大于负数,正数大于负数.
步骤:求绝对值,比较绝对值,比较负数的大小.
两个负数比较大小,绝对值大的反而小.
课堂小结
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
