1.4.1 有理数的加法 课件(共26张PPT)
文档属性
| 名称 | 1.4.1 有理数的加法 课件(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 18:28:09 | ||
图片预览





文档简介
1.4
有理数的加减
第1章
有理数
1.有理数的加法
学习目标
1.了解有理数加法的意义,理解有理数加法法则的合理性.
2.能运用该法则准确进行有理数的加法运算.(重点)
3.经历探索有理数加法法则的过程,理解并掌握有理数加法的法则.(难点)
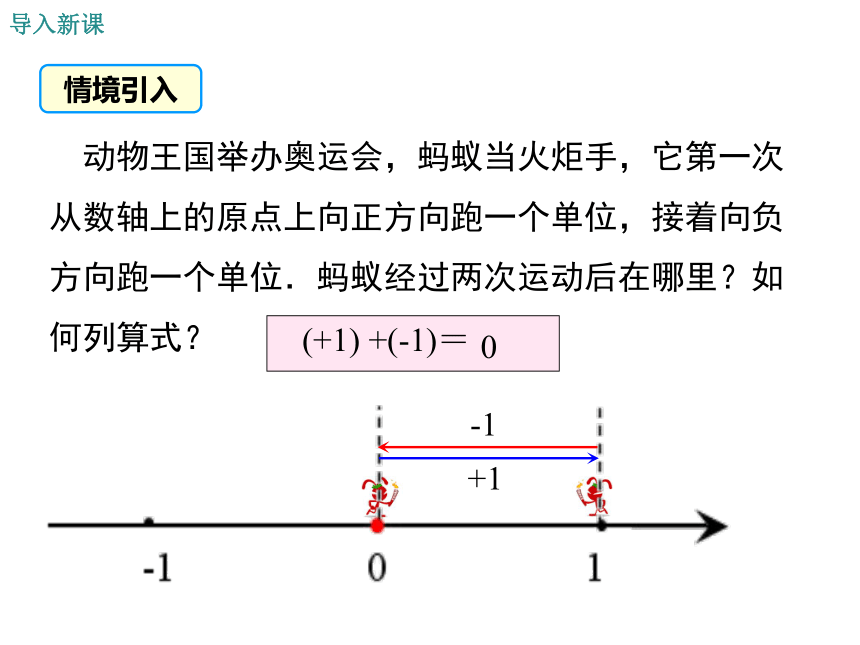
动物王国举办奥运会,蚂蚁当火炬手,它第一次从数轴上的原点上向正方向跑一个单位,接着向负方向跑一个单位.蚂蚁经过两次运动后在哪里?如何列算式?
+1
-1
(+1)
+(-1)=
0
导入新课
情境引入
若灰太狼在一条东西跑道上,先跑了20米,又跑了30米,我们规定向西为负,向东为正,即向东运动5米记作
5米,向西运动5米
记作
-5米.
东
西
讲授新课
有理数的加法法则
一
问题
能否确定它现在位于原来位置的哪个方向,与
原来位置相距多少米?
两次跑的方向不确定,最后位置也不确定
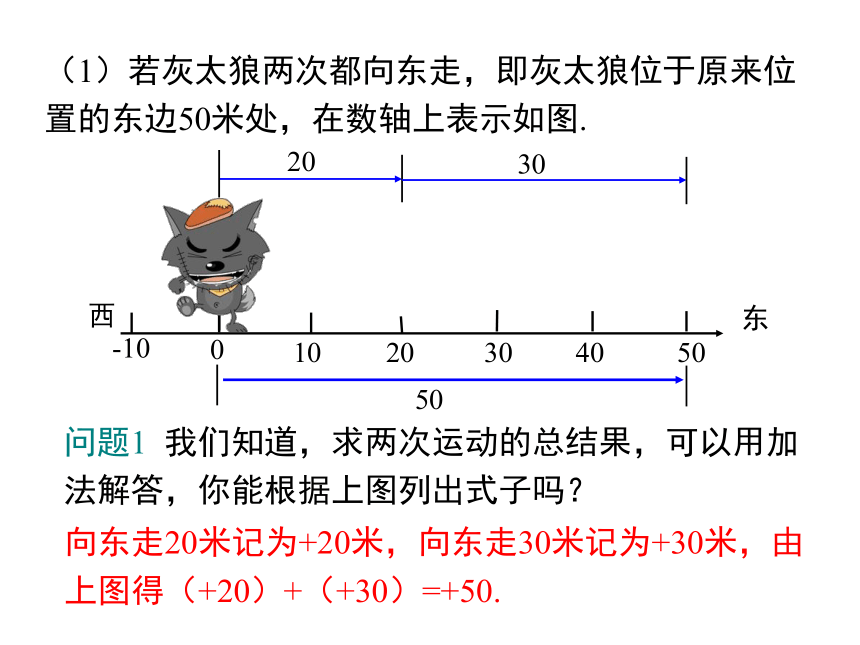
(1)若灰太狼两次都向东走,即灰太狼位于原来位置的东边50米处,在数轴上表示如图.
0
10
20
30
40
50
20
30
50
向东走20米记为+20米,向东走30米记为+30米,由
上图得(+20)+(+30)=+50.
东
西
-10
问题1
我们知道,求两次运动的总结果,可以用加
法解答,你能根据上图列出式子吗?
-10
0
-20
-30
-40
-50
20
30
50
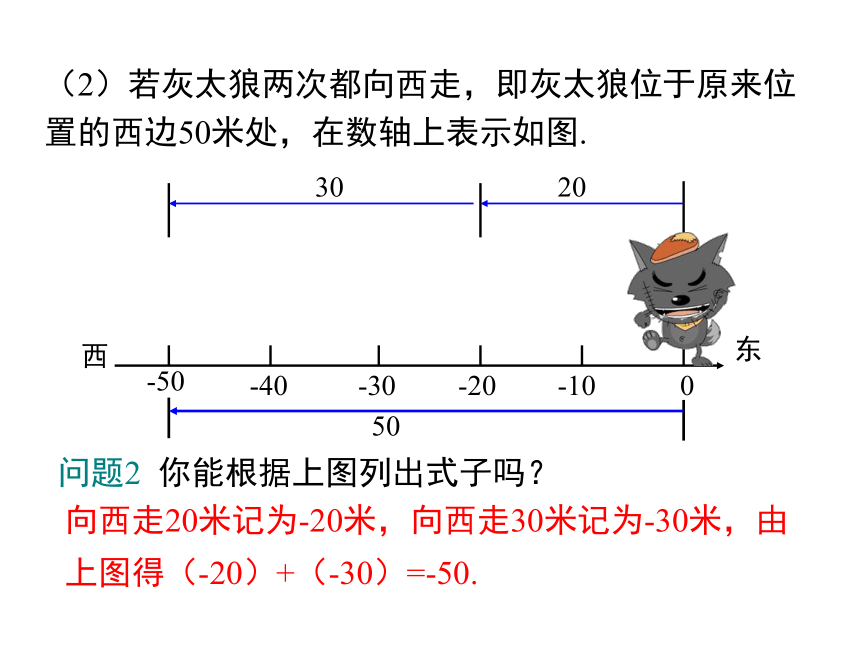
向西走20米记为-20米,向西走30米记为-30米,由
上图得(-20)+(-30)=-50.
东
西
(2)若灰太狼两次都向西走,即灰太狼位于原来位置的西边50米处,在数轴上表示如图.
问题2
你能根据上图列出式子吗?
东
-10
10
30
20
-20
0
20
30
10
向东走20米记为+20米,向西走30米记为-30米,由
上图得(+20)+(-30)=-10.
西
(3)若灰太狼先向东走20米,再向西走30米,即灰太狼位于原来位置的西边10米处,在数轴上表示如图.
问题3
你能根据上图列出式子吗?
东
-10
10
30
20
-20
0
20
30
10
西
(4)若灰太狼先向西走20米,再向东走30米,即灰太狼位于原来位置的东边10米处,在数轴上表示如图.
问题4
你能根据上图列出式子吗?
向西走20米记为-20米,向东走30米记为+30米,由
上图得(-20)+(+30)=
+10.
东
-10
10
30
20
-20
0
20
20
20
西
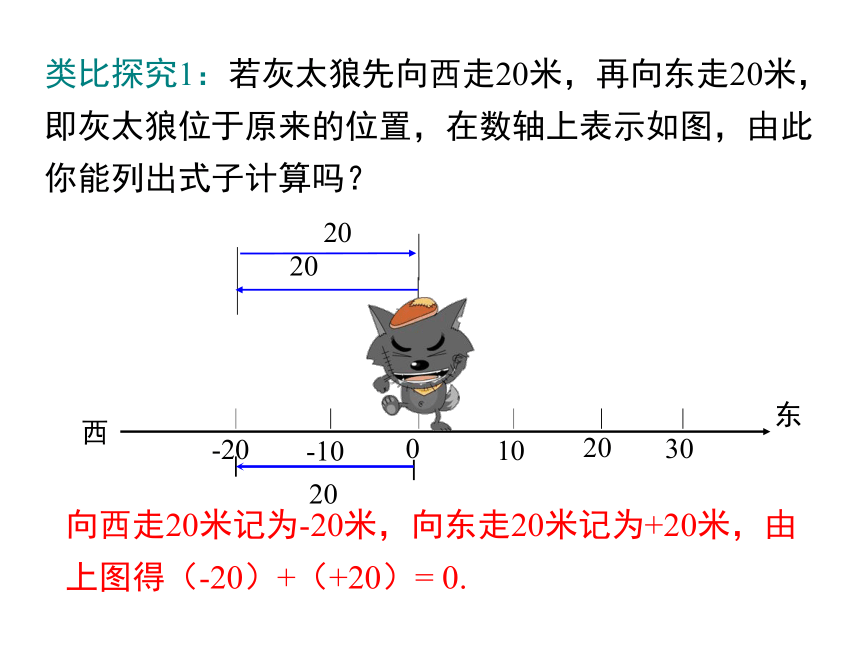
类比探究1:若灰太狼先向西走20米,再向东走20米,即灰太狼位于原来的位置,在数轴上表示如图,由此你能列出式子计算吗?
向西走20米记为-20米,向东走20米记为+20米,由
上图得(-20)+(+20)=
0.
东
-10
10
30
20
-20
0
20
西
类比探究2:若灰太狼先向西走20米,再原地不动,即灰太狼位于原来位置的西边20米处,在数轴上表示如图,由此你能列出式子计算吗?
向西走20米记为-20米,原地不动记为0米,由题图
得(-20)+0=
-20.
(+20)+(+30)=+50.
(-20)+(-30)=-50
(+20)+(-30)=-10
(-20)+(+30)=
+10
(-20)+(+20)=
0
(-20)+0=
-20
思考:观察前面的到的六个算式(如下),你能发现两个有理数相加,和的符号、和的绝对值是怎样确定的吗?
同号
异号
互为相反数
与零相加
得到的结果与两个加数的符号及绝对值有关
有理数加法法则
1.同号两数相加,结果取相同符号,并把绝对值
相加.
2.异号两数相加,绝对值相等时和为0;绝对值不
相等时,取绝对值较大的加数的符号,并用较
大的绝对值减较小的绝对值.
3.一个数同0相加,仍得这个数.
总结归纳
互为相反数的两数和总是0.
填表:
加数
加数
和的组成
和
符号
绝对值
-12
3
18
8
-9
16
-9
-5
﹣
12-3
﹣9
+
18+8
26
+
16-9
7
﹣
9+5
﹣14
注意:进行有理数加法运算时,应注意确定和的正负
号与绝对值.
练一练
例1
计算:
(1)(+7)+(+6);(2)(-5)+(-9);
(4)(-10.5)+(+21.5).
(3)
;
解:
(1)
(2)
(3)
(4)
典例精析
总结归纳
例2
计算:
(1)(-7.5)+(+7.5);
(2)(-3.5)+0.
解:
(1)(-7.5)+(+7.5)=0
(2)(-3.5)+0=-3.5.
互为相反数的两数和为0.
红队
黄队
蓝队
净胜球
红队
4:1
0:1
2
黄队
1:4
1:0
-2
蓝队
1:0
0:1
0
例3
足球循环赛中,红队胜黄队4:1,黄队胜蓝队1:0,蓝队胜红队1:0,计算各队的净胜球数.
分析:
有理数加法的应用
二
解:每个队的进球总数记为正数,失球总数记为负数,这两数的和为这队的净胜球数.
三场比赛中,红队共进4球,失2球,净胜球数为
(+4)+(-2)=+(4-2)=2
黄队共进2球,失4球,净胜球为
(+2)+(-4)=-(4-2)=-2
蓝队共进1球,失1球,净胜球数为
(+1)+(-1)=0.
红队
黄队
蓝队
净胜球
红队
4:1
0:1
2
黄队
1:4
1:0
-2
蓝队
1:0
0:1
0
海平面的高度为0m.一艘潜艇从海平面先下潜40m,再上升15m.求现在这艘潜艇相对于海平面的位置(上升为正,下潜为负).
解:潜水艇下潜40m,记作-40m;上升
15m,记作+15m.根据题意得
(-40)+(+15)=-(40-25)=-25(m)
答:现在这艘潜艇位于海平面下25m处.
-50m
-30m
-20m
海平面
-10m
0m
-40m
练一练
1.判断正误:
(1)两个负数相加,绝对值相减;
(2)正数加负数,和为负数;
(3)负数加正数,和为正数;
(4)两个有理数的和为负数时,这两个有理数都是
负数.
错误
错误
错误
错误
当堂练习
2.气温由-3℃上升2℃,此时的气温是( )
A.-2℃
B.-1℃
C.0℃
D.1℃
3.有理数a、b在数轴上的位置如图所示,则a+b的值( )
A.大于0
B.小于0
C.大于等于0
D.小于等于0
B
A
4.计算:
(1)(+2)+(-11);
(2)(-12)+(+12);
(3)
(4)(-3.4)+4.3.
5.股民默克上星期五以收盘价67元买进某公司股票
1000股,下表为本周内每日该股票的涨跌情况:
星 期
一
二
三
四
五
每股涨跌/元
4
4.5
-1
-2.5
-6
(1)星期三收盘时,每股多少元?
(2)本周内每股最高价为多少元?最低价为多少元?
解:(1)67+(+4)+(+4.5)+(-1)=74.5(元),
故星期三收盘时,每股74.5元;
星 期
一
二
三
四
五
每股涨跌/元
4
4.5
-1
-2.5
-6
(2)本周内每股最高价为多少元?最低价为多少元?
解:周一:67+4=71(元),
周二:71+4.5=75.5(元),
周三:75.5+(-1)=74.5(元),
周四:74.5+(-2.5)=72(元),
周五:72+(-6)=66(元),
所以本周内每股最高价为75.5元,最低价为66元.
拓展:6.已知│a│=
8,│b│=
2.
(1)当a、b同号时,求a+b的值;
(2)当a、b异号时,求a+b的值.
解:因为│a│=
8,│b│=
2,
所以a=
±8,b=±
2.
(1)因为a、b同号,
所以a=
8,b=
2或a=
-8,b=-
2.
所以a+b=±10;
(2)因为a、b异号,
所以a=
8,b=
-2或a=
-8,b=2.
所以a+b=±6.
课堂小结
确定类型
定符号
绝对值
同号
异号(绝对值不相等)
异号(互为相反数)
与0相加
相同符号
取绝对值较大的加数的符号
相加
相减
结果是0
仍是这个数
有理数的加法法则:
有理数的加减
第1章
有理数
1.有理数的加法
学习目标
1.了解有理数加法的意义,理解有理数加法法则的合理性.
2.能运用该法则准确进行有理数的加法运算.(重点)
3.经历探索有理数加法法则的过程,理解并掌握有理数加法的法则.(难点)
动物王国举办奥运会,蚂蚁当火炬手,它第一次从数轴上的原点上向正方向跑一个单位,接着向负方向跑一个单位.蚂蚁经过两次运动后在哪里?如何列算式?
+1
-1
(+1)
+(-1)=
0
导入新课
情境引入
若灰太狼在一条东西跑道上,先跑了20米,又跑了30米,我们规定向西为负,向东为正,即向东运动5米记作
5米,向西运动5米
记作
-5米.
东
西
讲授新课
有理数的加法法则
一
问题
能否确定它现在位于原来位置的哪个方向,与
原来位置相距多少米?
两次跑的方向不确定,最后位置也不确定
(1)若灰太狼两次都向东走,即灰太狼位于原来位置的东边50米处,在数轴上表示如图.
0
10
20
30
40
50
20
30
50
向东走20米记为+20米,向东走30米记为+30米,由
上图得(+20)+(+30)=+50.
东
西
-10
问题1
我们知道,求两次运动的总结果,可以用加
法解答,你能根据上图列出式子吗?
-10
0
-20
-30
-40
-50
20
30
50
向西走20米记为-20米,向西走30米记为-30米,由
上图得(-20)+(-30)=-50.
东
西
(2)若灰太狼两次都向西走,即灰太狼位于原来位置的西边50米处,在数轴上表示如图.
问题2
你能根据上图列出式子吗?
东
-10
10
30
20
-20
0
20
30
10
向东走20米记为+20米,向西走30米记为-30米,由
上图得(+20)+(-30)=-10.
西
(3)若灰太狼先向东走20米,再向西走30米,即灰太狼位于原来位置的西边10米处,在数轴上表示如图.
问题3
你能根据上图列出式子吗?
东
-10
10
30
20
-20
0
20
30
10
西
(4)若灰太狼先向西走20米,再向东走30米,即灰太狼位于原来位置的东边10米处,在数轴上表示如图.
问题4
你能根据上图列出式子吗?
向西走20米记为-20米,向东走30米记为+30米,由
上图得(-20)+(+30)=
+10.
东
-10
10
30
20
-20
0
20
20
20
西
类比探究1:若灰太狼先向西走20米,再向东走20米,即灰太狼位于原来的位置,在数轴上表示如图,由此你能列出式子计算吗?
向西走20米记为-20米,向东走20米记为+20米,由
上图得(-20)+(+20)=
0.
东
-10
10
30
20
-20
0
20
西
类比探究2:若灰太狼先向西走20米,再原地不动,即灰太狼位于原来位置的西边20米处,在数轴上表示如图,由此你能列出式子计算吗?
向西走20米记为-20米,原地不动记为0米,由题图
得(-20)+0=
-20.
(+20)+(+30)=+50.
(-20)+(-30)=-50
(+20)+(-30)=-10
(-20)+(+30)=
+10
(-20)+(+20)=
0
(-20)+0=
-20
思考:观察前面的到的六个算式(如下),你能发现两个有理数相加,和的符号、和的绝对值是怎样确定的吗?
同号
异号
互为相反数
与零相加
得到的结果与两个加数的符号及绝对值有关
有理数加法法则
1.同号两数相加,结果取相同符号,并把绝对值
相加.
2.异号两数相加,绝对值相等时和为0;绝对值不
相等时,取绝对值较大的加数的符号,并用较
大的绝对值减较小的绝对值.
3.一个数同0相加,仍得这个数.
总结归纳
互为相反数的两数和总是0.
填表:
加数
加数
和的组成
和
符号
绝对值
-12
3
18
8
-9
16
-9
-5
﹣
12-3
﹣9
+
18+8
26
+
16-9
7
﹣
9+5
﹣14
注意:进行有理数加法运算时,应注意确定和的正负
号与绝对值.
练一练
例1
计算:
(1)(+7)+(+6);(2)(-5)+(-9);
(4)(-10.5)+(+21.5).
(3)
;
解:
(1)
(2)
(3)
(4)
典例精析
总结归纳
例2
计算:
(1)(-7.5)+(+7.5);
(2)(-3.5)+0.
解:
(1)(-7.5)+(+7.5)=0
(2)(-3.5)+0=-3.5.
互为相反数的两数和为0.
红队
黄队
蓝队
净胜球
红队
4:1
0:1
2
黄队
1:4
1:0
-2
蓝队
1:0
0:1
0
例3
足球循环赛中,红队胜黄队4:1,黄队胜蓝队1:0,蓝队胜红队1:0,计算各队的净胜球数.
分析:
有理数加法的应用
二
解:每个队的进球总数记为正数,失球总数记为负数,这两数的和为这队的净胜球数.
三场比赛中,红队共进4球,失2球,净胜球数为
(+4)+(-2)=+(4-2)=2
黄队共进2球,失4球,净胜球为
(+2)+(-4)=-(4-2)=-2
蓝队共进1球,失1球,净胜球数为
(+1)+(-1)=0.
红队
黄队
蓝队
净胜球
红队
4:1
0:1
2
黄队
1:4
1:0
-2
蓝队
1:0
0:1
0
海平面的高度为0m.一艘潜艇从海平面先下潜40m,再上升15m.求现在这艘潜艇相对于海平面的位置(上升为正,下潜为负).
解:潜水艇下潜40m,记作-40m;上升
15m,记作+15m.根据题意得
(-40)+(+15)=-(40-25)=-25(m)
答:现在这艘潜艇位于海平面下25m处.
-50m
-30m
-20m
海平面
-10m
0m
-40m
练一练
1.判断正误:
(1)两个负数相加,绝对值相减;
(2)正数加负数,和为负数;
(3)负数加正数,和为正数;
(4)两个有理数的和为负数时,这两个有理数都是
负数.
错误
错误
错误
错误
当堂练习
2.气温由-3℃上升2℃,此时的气温是( )
A.-2℃
B.-1℃
C.0℃
D.1℃
3.有理数a、b在数轴上的位置如图所示,则a+b的值( )
A.大于0
B.小于0
C.大于等于0
D.小于等于0
B
A
4.计算:
(1)(+2)+(-11);
(2)(-12)+(+12);
(3)
(4)(-3.4)+4.3.
5.股民默克上星期五以收盘价67元买进某公司股票
1000股,下表为本周内每日该股票的涨跌情况:
星 期
一
二
三
四
五
每股涨跌/元
4
4.5
-1
-2.5
-6
(1)星期三收盘时,每股多少元?
(2)本周内每股最高价为多少元?最低价为多少元?
解:(1)67+(+4)+(+4.5)+(-1)=74.5(元),
故星期三收盘时,每股74.5元;
星 期
一
二
三
四
五
每股涨跌/元
4
4.5
-1
-2.5
-6
(2)本周内每股最高价为多少元?最低价为多少元?
解:周一:67+4=71(元),
周二:71+4.5=75.5(元),
周三:75.5+(-1)=74.5(元),
周四:74.5+(-2.5)=72(元),
周五:72+(-6)=66(元),
所以本周内每股最高价为75.5元,最低价为66元.
拓展:6.已知│a│=
8,│b│=
2.
(1)当a、b同号时,求a+b的值;
(2)当a、b异号时,求a+b的值.
解:因为│a│=
8,│b│=
2,
所以a=
±8,b=±
2.
(1)因为a、b同号,
所以a=
8,b=
2或a=
-8,b=-
2.
所以a+b=±10;
(2)因为a、b异号,
所以a=
8,b=
-2或a=
-8,b=2.
所以a+b=±6.
课堂小结
确定类型
定符号
绝对值
同号
异号(绝对值不相等)
异号(互为相反数)
与0相加
相同符号
取绝对值较大的加数的符号
相加
相减
结果是0
仍是这个数
有理数的加法法则:
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
