人教版七年级下册数学:5.2 平行线的性质与判定专题训练课件 (共18张PPT)
文档属性
| 名称 | 人教版七年级下册数学:5.2 平行线的性质与判定专题训练课件 (共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:00:00 | ||
图片预览


文档简介
第五章 相交线与平行线
专题训练 平行线的性质与判定
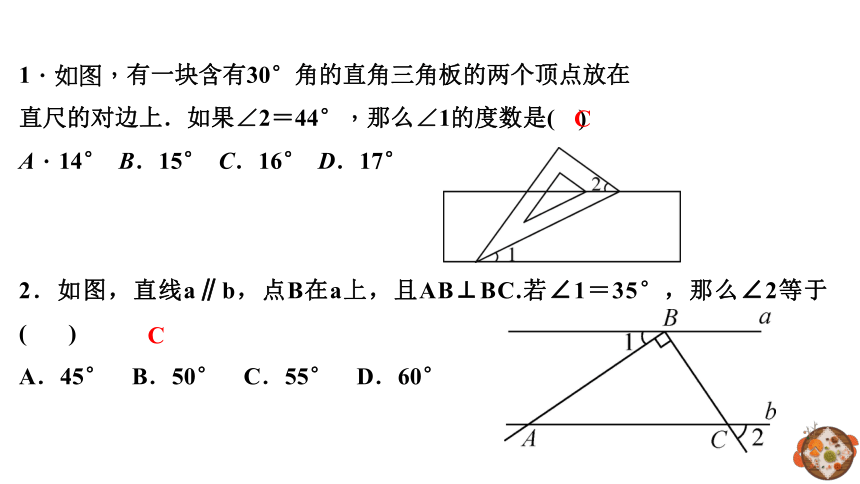
1.如图,有一块含有30°角的直角三角板的两个顶点放在
直尺的对边上.如果∠2=44°,那么∠1的度数是( )
A.14° B.15° C.16° D.17°
2.如图,直线a∥b,点B在a上,且AB⊥BC.若∠1=35°,那么∠2等于( )
A.45° B.50° C.55° D.60°
C
C
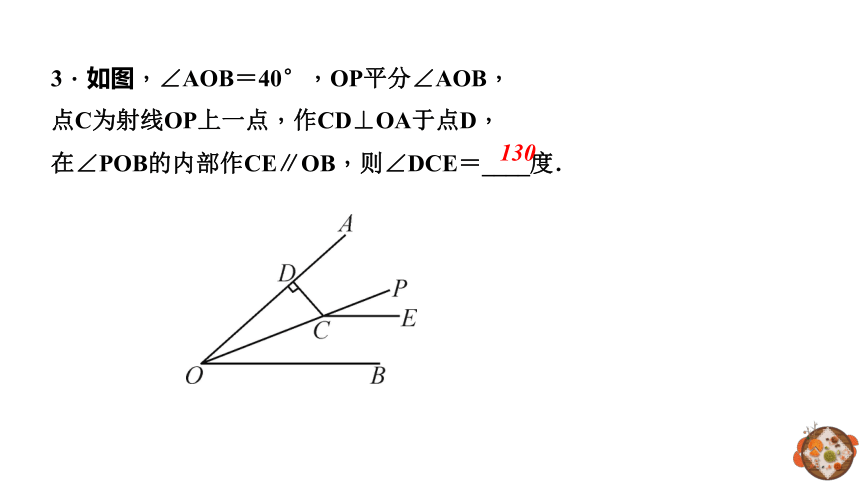
3.如图,∠AOB=40°,OP平分∠AOB,
点C为射线OP上一点,作CD⊥OA于点D,
在∠POB的内部作CE∥OB,则∠DCE=____度.
130
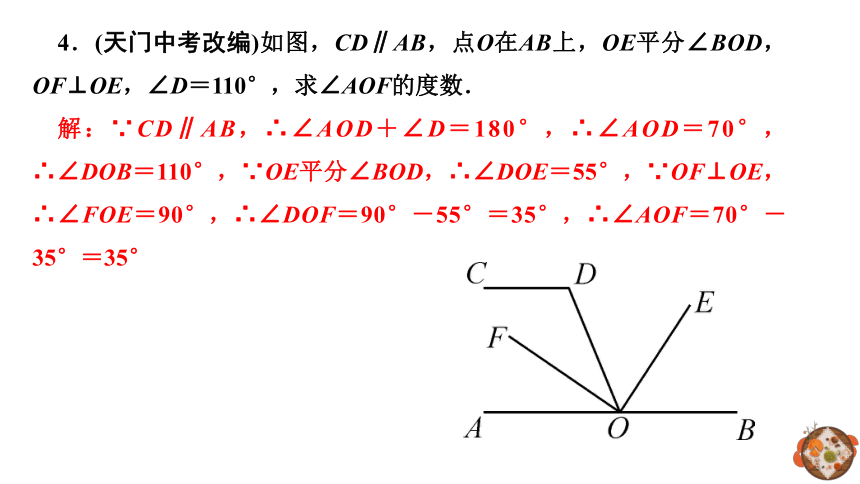
4.(天门中考改编)如图,CD∥AB,点O在AB上,OE平分∠BOD,OF⊥OE,∠D=110°,求∠AOF的度数.
解:∵CD∥AB,∴∠AOD+∠D=180°,∴∠AOD=70°,∴∠DOB=110°,∵OE平分∠BOD,∴∠DOE=55°,∵OF⊥OE,∴∠FOE=90°,∴∠DOF=90°-55°=35°,∴∠AOF=70°-35°=35°
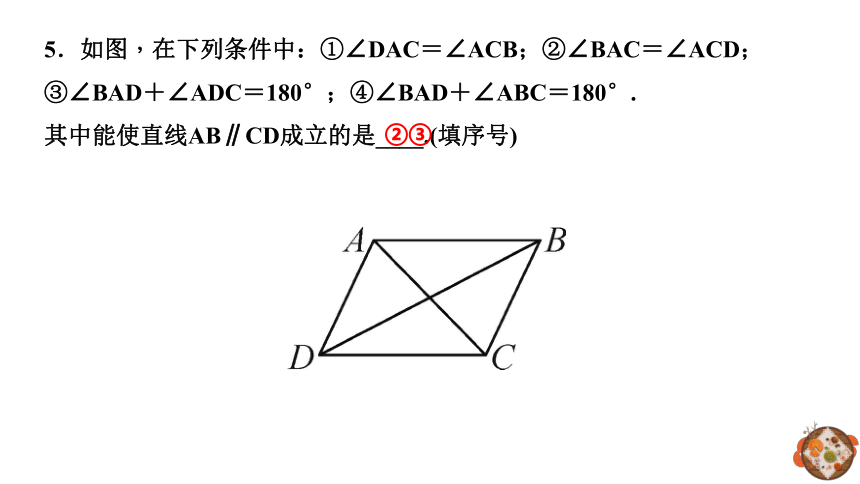
5.如图,在下列条件中:①∠DAC=∠ACB;②∠BAC=∠ACD;
③∠BAD+∠ADC=180°;④∠BAD+∠ABC=180°.
其中能使直线AB∥CD成立的是____.(填序号)
②③
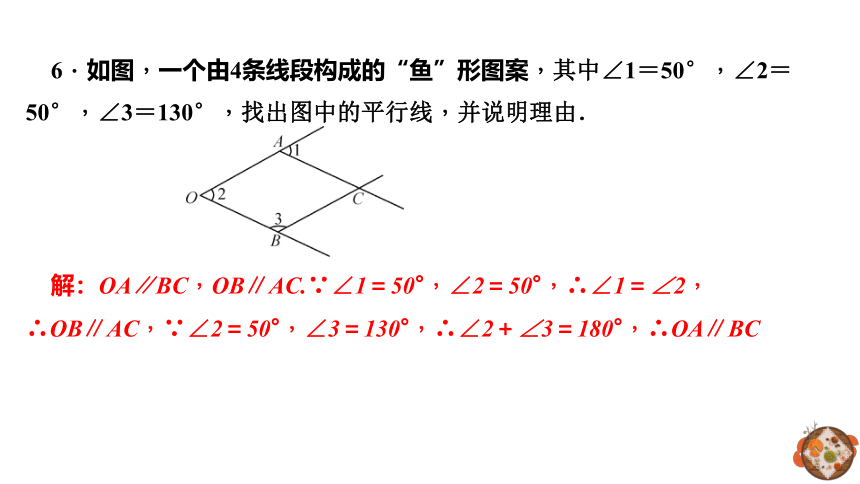
6.如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.
解:OA∥BC,OB∥AC.∵∠1=50°,∠2=50°,∴∠1=∠2,∴OB∥AC,∵∠2=50°,∠3=130°,∴∠2+∠3=180°,∴OA∥BC
7.如图所示,∠A=120°,∠B=60°,∠EFC=∠DCG,试说明AD∥EF.
解:∵∠A=120°,∠B=60°(已知),∠A+∠B=120°+60°=180°(等式性质),∴AD∥BC(同旁内角互补,两直线平行).∵∠EFC=∠DCG(已知),∴EF∥BC(内错角相等,两直线平行),∴AD∥EF(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
8.(益阳中考)如图,AB∥CD,∠1=∠2.试说明AM∥CN.
解:∵AB∥CD,∴∠EAB=∠ECD,∵∠1=∠2,∴∠EAM=∠ECN,∴AM∥CN
9.如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠1,试问:AD是∠BAC的平分线吗?若是,请说明理由.
解:是.理由略
10.如图AD⊥BC于点D,EG⊥BC于点G,∠E=∠1,
试问:AD是∠BAC的平分线吗?若是,请说明理由.
解:是.理由略
11.如图,AE∥CF,∠A=∠C.
(1)若∠1=35°,求∠2的度数;
(2)判断AD与BC的位置关系,并说明理由;
(3)若DA平分∠BDF,试说明BC平分∠DBE.
平行线相关的探究问题
12.在一次数学拓展课上,老师提出了这样一个问题:“如果一个角的两边与另一个角的两边分别平行,请探究这两个角之间的关系”,小明同学根据题意画出了以下两个不同的图形,请你结合图形完成以下探究过程:
(1)如图①,如果AB∥CD,BE∥DF,那么∠1与∠2的关系是__________.
如图②,如果AB∥CD,BE∥DF,那么∠1与∠2的关系是_____________;
∠2=∠1
∠1+∠2=180°
(2)根据(1)的探究过程,我们可得出结论:如果一个角的两边与另一个角的两边分别平行,那么这两个角________________;
(3)利用结论解决问题:如果有两个角的两边分别平行,且一个角比另一个角的3倍少60°,则这两个角分别是多少度?
相等或互补
解:(1)∠2=∠1;∠1+∠2=180°
(2)相等或互补
(3)设一个角为x°,则另一个角为(3x-60)°,分两种情况:①x=3x-60,x=30,3x-60=30;②x+3x-60=180,x=60,180°-60°=120°,
答:则这两个角分别是30°,30°或60°,120°
13.探究:如图①,已知直线l1∥l2,直线l3和l1,l2分别交于点C和D,直线l3上有一点P.
(1)若点P在点C,D之间运动,问∠PAC,∠APB,∠PBD之间有怎样的关系?并说明理由;
(2)若点P在C,D两点的外侧运动(点P与点C,D不重合),请尝试自己画图,写出∠PAC,∠APB,∠PBD之间的关系,并说明理由;
(3)如图②,AB∥EF,∠C=90°,我们可以用类似的方法求出∠α,∠β,∠γ之间的关系,请直接写出∠α,∠β,∠γ之间的关系.
解:(1)如图①,当P点在点C,D之间运动时,∠APB=∠PAC+∠PBD.理由如下:过点P作PE∥l1,∵l1∥l2,∴PE∥l2∥l1,∴∠PAC=∠1,∠PBD=∠2,∴∠APB=∠1+∠2=∠PAC+∠PBD
(2)如图甲,当点P在C,D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB.理由如下:
∵l1∥l2,∴∠PEC=∠PBD,∵∠PEC=∠PAC+∠APB,∴∠PBD=∠PAC+∠APB.如图乙,当点P在C,D两点的外侧运动,且在l2下方时,∠PAC=∠PBD+∠APB.理由如下:∵l1∥l2,∴∠PED=∠PAC,∵∠PED=∠PBD+∠APB,∴∠PAC=∠PBD+∠APB
(3)∠α+∠β-∠γ=90°
专题训练 平行线的性质与判定
1.如图,有一块含有30°角的直角三角板的两个顶点放在
直尺的对边上.如果∠2=44°,那么∠1的度数是( )
A.14° B.15° C.16° D.17°
2.如图,直线a∥b,点B在a上,且AB⊥BC.若∠1=35°,那么∠2等于( )
A.45° B.50° C.55° D.60°
C
C
3.如图,∠AOB=40°,OP平分∠AOB,
点C为射线OP上一点,作CD⊥OA于点D,
在∠POB的内部作CE∥OB,则∠DCE=____度.
130
4.(天门中考改编)如图,CD∥AB,点O在AB上,OE平分∠BOD,OF⊥OE,∠D=110°,求∠AOF的度数.
解:∵CD∥AB,∴∠AOD+∠D=180°,∴∠AOD=70°,∴∠DOB=110°,∵OE平分∠BOD,∴∠DOE=55°,∵OF⊥OE,∴∠FOE=90°,∴∠DOF=90°-55°=35°,∴∠AOF=70°-35°=35°
5.如图,在下列条件中:①∠DAC=∠ACB;②∠BAC=∠ACD;
③∠BAD+∠ADC=180°;④∠BAD+∠ABC=180°.
其中能使直线AB∥CD成立的是____.(填序号)
②③
6.如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.
解:OA∥BC,OB∥AC.∵∠1=50°,∠2=50°,∴∠1=∠2,∴OB∥AC,∵∠2=50°,∠3=130°,∴∠2+∠3=180°,∴OA∥BC
7.如图所示,∠A=120°,∠B=60°,∠EFC=∠DCG,试说明AD∥EF.
解:∵∠A=120°,∠B=60°(已知),∠A+∠B=120°+60°=180°(等式性质),∴AD∥BC(同旁内角互补,两直线平行).∵∠EFC=∠DCG(已知),∴EF∥BC(内错角相等,两直线平行),∴AD∥EF(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
8.(益阳中考)如图,AB∥CD,∠1=∠2.试说明AM∥CN.
解:∵AB∥CD,∴∠EAB=∠ECD,∵∠1=∠2,∴∠EAM=∠ECN,∴AM∥CN
9.如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠1,试问:AD是∠BAC的平分线吗?若是,请说明理由.
解:是.理由略
10.如图AD⊥BC于点D,EG⊥BC于点G,∠E=∠1,
试问:AD是∠BAC的平分线吗?若是,请说明理由.
解:是.理由略
11.如图,AE∥CF,∠A=∠C.
(1)若∠1=35°,求∠2的度数;
(2)判断AD与BC的位置关系,并说明理由;
(3)若DA平分∠BDF,试说明BC平分∠DBE.
平行线相关的探究问题
12.在一次数学拓展课上,老师提出了这样一个问题:“如果一个角的两边与另一个角的两边分别平行,请探究这两个角之间的关系”,小明同学根据题意画出了以下两个不同的图形,请你结合图形完成以下探究过程:
(1)如图①,如果AB∥CD,BE∥DF,那么∠1与∠2的关系是__________.
如图②,如果AB∥CD,BE∥DF,那么∠1与∠2的关系是_____________;
∠2=∠1
∠1+∠2=180°
(2)根据(1)的探究过程,我们可得出结论:如果一个角的两边与另一个角的两边分别平行,那么这两个角________________;
(3)利用结论解决问题:如果有两个角的两边分别平行,且一个角比另一个角的3倍少60°,则这两个角分别是多少度?
相等或互补
解:(1)∠2=∠1;∠1+∠2=180°
(2)相等或互补
(3)设一个角为x°,则另一个角为(3x-60)°,分两种情况:①x=3x-60,x=30,3x-60=30;②x+3x-60=180,x=60,180°-60°=120°,
答:则这两个角分别是30°,30°或60°,120°
13.探究:如图①,已知直线l1∥l2,直线l3和l1,l2分别交于点C和D,直线l3上有一点P.
(1)若点P在点C,D之间运动,问∠PAC,∠APB,∠PBD之间有怎样的关系?并说明理由;
(2)若点P在C,D两点的外侧运动(点P与点C,D不重合),请尝试自己画图,写出∠PAC,∠APB,∠PBD之间的关系,并说明理由;
(3)如图②,AB∥EF,∠C=90°,我们可以用类似的方法求出∠α,∠β,∠γ之间的关系,请直接写出∠α,∠β,∠γ之间的关系.
解:(1)如图①,当P点在点C,D之间运动时,∠APB=∠PAC+∠PBD.理由如下:过点P作PE∥l1,∵l1∥l2,∴PE∥l2∥l1,∴∠PAC=∠1,∠PBD=∠2,∴∠APB=∠1+∠2=∠PAC+∠PBD
(2)如图甲,当点P在C,D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB.理由如下:
∵l1∥l2,∴∠PEC=∠PBD,∵∠PEC=∠PAC+∠APB,∴∠PBD=∠PAC+∠APB.如图乙,当点P在C,D两点的外侧运动,且在l2下方时,∠PAC=∠PBD+∠APB.理由如下:∵l1∥l2,∴∠PED=∠PAC,∵∠PED=∠PBD+∠APB,∴∠PAC=∠PBD+∠APB
(3)∠α+∠β-∠γ=90°
