人教版八年级上册14.3.1 提公因式法课件(24张)
文档属性
| 名称 | 人教版八年级上册14.3.1 提公因式法课件(24张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 110.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 20:36:43 | ||
图片预览







文档简介
第十四章 整式的乘法与因式分解
14.3 因式分解
第1课时 提公因式法
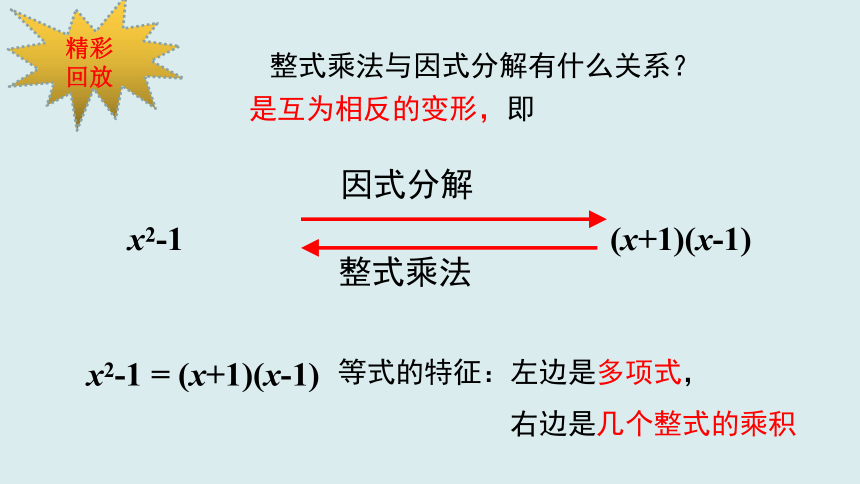
x2-1 (x+1)(x-1)
因式分解
整式乘法
x2-1 = (x+1)(x-1)
等式的特征:左边是多项式,
右边是几个整式的乘积
整式乘法与因式分解有什么关系?
是互为相反的变形,即
精彩回放
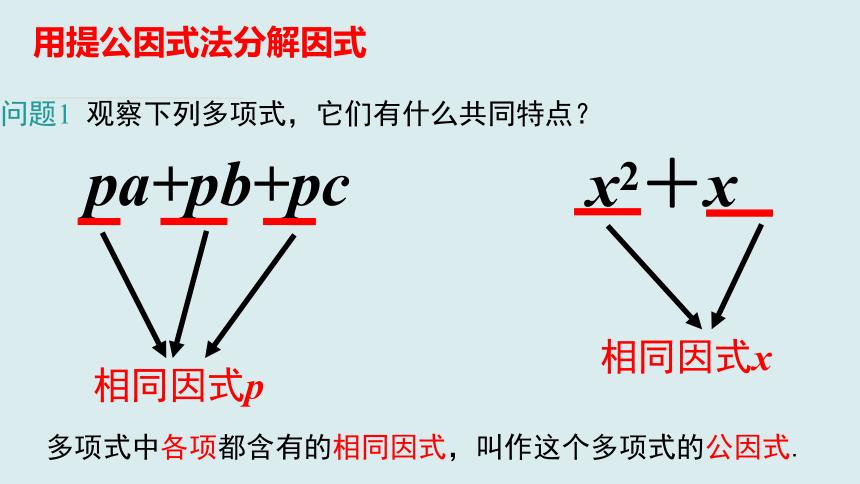
pa+pb+pc
用提公因式法分解因式
多项式中各项都含有的相同因式,叫作这个多项式的公因式.
相同因式p
问题1 观察下列多项式,它们有什么共同特点?
x2+x
相同因式x
一般地,如果多项式的各项有公因式,可以把这个公因式提取出来,将多项式写成公因式与另一个因式的乘积的形式,这种分解因式的方法叫做提公因式法.
( a+b+c )
pa+ pb +pc
p
=
1.把一个多项式化成几个______________的形式叫做把这个多项式因式分解.
2.因式分解与________________互为逆变形.
3.多项式各项公共的因式叫做这个多项式的_____________.
4.把多项式中____________提出来,从而达到因式分解的目的,这种分解因式的方法叫做提公因式法.
整式的积
整式乘法
公因式
公因式
基础知识检测
因式分解:
(1)3a3c2+12ab3c;
(2)2a(b+c)-3(b+c);
(3)(a+b)(a-b)-a-b.
针对训练
(3)原式=(a+b)(a-b-1).
解:(1)原式=3ac(a2c+4b3);
(2)原式=(2a-3)(b+c);
因式分解的概念
1.(3分)(2017·常德)下列各式由左到右的变形中,属于分解因式的是( )
A.a(m+n)=am+an
B.a2-b2-c2=(a-b)(a+b)-c2
C.10x2-5x=5x(2x-1)
D.x2-16+6x=(x+4)(x-4)+6x
2.(4分)在公式(a+b)(a-b)=a2-b2,从左到右的变形是____________,从右到左的变形是__________________.
C
整式乘法
因式分解
3.多项式15m3n2+5m2n-20m2n3的公因式是( )
A.5mn B.5m2n2 C.5m2n D .5mn2
4.把多项式(x+2)(x-2)+(x-2)提取公因式(x-2)后,余下的部分是( )
A.x+1 B.2x C.x+2 D.x+3
C
D
5.(3分)下列各组多项式没有公因式的是( )
A.2x-2y与y-x
B.x2-xy与xy-y2
C.3x+y与x+3y
D.5x+10y与-2y-x
6.(3分)下列多项式能用提公因式法分解因式的是( )
A.a2-4 B.a2+b2
C.a2+3a D.2a2-4a+1
C
C
7.下列多项式的分解因式,正确的是( )
A.12xyz-9x2y2=3xyz(4-3xyz)
B.3a2y-3ay+6y=3y(a2-a+2)
C.-x2+xy-xz=-x(x2+y-z)
D.a2b+5ab-b=b(a2+5a)
B
8.(3分)多项式9x3y-36xy3+3xy的公因式为___________.
9.(4分)分解因式:
(1)(盐城中考)a2-ab=______________;
(2)(南京中考)2a(b+c)-3(b+c)=_______________________.
10.(12分)分解因式:
(1)x2y-2x2y3-3x3y;
解:原式=x2y(1-2y2-3x)
3xy
a(a-b)
(b+c)(2a-3)
11.把下列各式分解因式:
(1)8 m2n+2mn=_____________;
(2)12xyz-9x2y2=_____________;
(3)p(a2 + b2 )- q(a2 + b2 )=_____________;
(4) -x3y3-x2y2-xy=_______________;
2mn(4m+1)
3xy(4z-3xy)
(a2+b2)(p-q)
-xy(x2y2+xy+1)
(5)(x-y)2+y(y-x)=_____________.
(y-x)(2y-x)
(1)6p(p+a)-4a(p+a);
解:原式=2(p+a)(3p-2a)
(2)(x+3)2-(x+3);
解:原式=(x+3)(x+2)
(3)(a-b)3-(b-a)2.
解:原式=(a-b)2(a-b-1)
12 计算
13. 简便计算:
(1) 1.992+1.99×0.01 ; (2)20132+2013-20142;
(3)(-2)101+(-2)100.
(2) 原式=2013(2013+1)-20142
=2013×2014-20142=2014×(2013-2014)
=-2014.
解:(1) 原式=1.99(1.99+0.01)=3.98;
(3)原式=(-2)100 ×(-2+1) =2100 ×(-1)=-2100.
14.(8分)(1)计算:53.6×1.6+18.4×53.6-20×53.6;
解:原式=53.6×(1.6+18.4-20)=0
(2)(黔南州中考)若ab=2,a-b=-1,求代数式a2b-ab2的值.
解:原式=ab(a-b)=-2
15 已知a+b=7,ab=4,求a2b+ab2的值.
∴原式=ab(a+b)=4×7=28.
解:∵a+b=7,ab=4,
方法总结:
含a±b,ab的求值题,通常要将所求代数式进行因式分解,将其变形为能用a±b和ab表示的式子,然后将a±b,ab的值整体带入即可.
二、填空题(每小题3分,共9分)
16.如果把多项式x2-3x+n分解因式得(x-1)(x+m),那么m=_______,n=____.
17.多项式12x3y3z-8x3y2z3+6x4y2z2的公因式是_____________.
18.因式分解:m2-mn+mx-nx=_____________________.
-2
2
2x3y2z
(m-n)(m+x)
解:(1)2x2y+xy2=xy(2x+y)=3 ×4=12.
(2)原式=(2x+1)[(2x+1)-(2x-1)]
=(2x+1)(2x+1-2x+1)=2(2x+1).
19.(1)已知: 2x+y=4,xy=3,求代数式2x2y+xy2的值.
(2)化简求值:(2x+1)2-(2x+1)(2x-1),其中x=0.5 .
将x= 0.5 代入上式,得
原式=4.
三、解答题(共36分)
20.(12分)分解因式:
(1)-27m2n+9mn2-18mn;
解:原式=-9mn(3m-n+2)
(2)x(x-y)(a-b)-y(y-x)(b-a);
解:原式=(x-y)2(a-b)
(3)(a+1)2+(a2+a)2.
解:原式=(a+1)2(1+a2)
(2)已知a,b,c为△ABC的三边,且a2-ab+4ac-4bc=0,试判断△ABC的形状.
解:∵a(a-b)+4c(a-b)=0,∴(a-b)(a+4c)=0,又∵a+4c≠0,∴a-b=0,∴a=b,即△ABC为等腰三角形
解:原式=-2mn(m+n)=1
21.△ABC的三边长分别为a、b、c,且a+2ab=c+2bc,请判断△ABC是等边三角形、等腰三角形还是直角三角形?并说明理由.
拓展提升
∴△ABC是等腰三角形.
解:整理a+2ab=c+2bc得,a+2ab-c-2bc=0,
(a-c)+2b(a-c)=0,(a-c)(1+2b)=0,
∴a-c=0或1+2b=0,
即a=c或b=-0.5(舍去),
【综合运用】
22.(12分)阅读下列因式分解的过程,再回答所提出的问题:
1+x+x(x+1)+x(x+1)2
=(1+x)[1+x+x(1+x)]
=(1+x)2(1+x)
=(1+x)3
(1)上述分解因式的方法是______________法,共应用了____次.
(2)若分解1+x+x(x+1)+x(x+1)2+…+x(x+1)2 019,则需要应用上述方法_______________次,分解因式后的结果是_________________.
提公因式
2
2 019
(1+x)2 020
谢谢观看
14.3 因式分解
第1课时 提公因式法
x2-1 (x+1)(x-1)
因式分解
整式乘法
x2-1 = (x+1)(x-1)
等式的特征:左边是多项式,
右边是几个整式的乘积
整式乘法与因式分解有什么关系?
是互为相反的变形,即
精彩回放
pa+pb+pc
用提公因式法分解因式
多项式中各项都含有的相同因式,叫作这个多项式的公因式.
相同因式p
问题1 观察下列多项式,它们有什么共同特点?
x2+x
相同因式x
一般地,如果多项式的各项有公因式,可以把这个公因式提取出来,将多项式写成公因式与另一个因式的乘积的形式,这种分解因式的方法叫做提公因式法.
( a+b+c )
pa+ pb +pc
p
=
1.把一个多项式化成几个______________的形式叫做把这个多项式因式分解.
2.因式分解与________________互为逆变形.
3.多项式各项公共的因式叫做这个多项式的_____________.
4.把多项式中____________提出来,从而达到因式分解的目的,这种分解因式的方法叫做提公因式法.
整式的积
整式乘法
公因式
公因式
基础知识检测
因式分解:
(1)3a3c2+12ab3c;
(2)2a(b+c)-3(b+c);
(3)(a+b)(a-b)-a-b.
针对训练
(3)原式=(a+b)(a-b-1).
解:(1)原式=3ac(a2c+4b3);
(2)原式=(2a-3)(b+c);
因式分解的概念
1.(3分)(2017·常德)下列各式由左到右的变形中,属于分解因式的是( )
A.a(m+n)=am+an
B.a2-b2-c2=(a-b)(a+b)-c2
C.10x2-5x=5x(2x-1)
D.x2-16+6x=(x+4)(x-4)+6x
2.(4分)在公式(a+b)(a-b)=a2-b2,从左到右的变形是____________,从右到左的变形是__________________.
C
整式乘法
因式分解
3.多项式15m3n2+5m2n-20m2n3的公因式是( )
A.5mn B.5m2n2 C.5m2n D .5mn2
4.把多项式(x+2)(x-2)+(x-2)提取公因式(x-2)后,余下的部分是( )
A.x+1 B.2x C.x+2 D.x+3
C
D
5.(3分)下列各组多项式没有公因式的是( )
A.2x-2y与y-x
B.x2-xy与xy-y2
C.3x+y与x+3y
D.5x+10y与-2y-x
6.(3分)下列多项式能用提公因式法分解因式的是( )
A.a2-4 B.a2+b2
C.a2+3a D.2a2-4a+1
C
C
7.下列多项式的分解因式,正确的是( )
A.12xyz-9x2y2=3xyz(4-3xyz)
B.3a2y-3ay+6y=3y(a2-a+2)
C.-x2+xy-xz=-x(x2+y-z)
D.a2b+5ab-b=b(a2+5a)
B
8.(3分)多项式9x3y-36xy3+3xy的公因式为___________.
9.(4分)分解因式:
(1)(盐城中考)a2-ab=______________;
(2)(南京中考)2a(b+c)-3(b+c)=_______________________.
10.(12分)分解因式:
(1)x2y-2x2y3-3x3y;
解:原式=x2y(1-2y2-3x)
3xy
a(a-b)
(b+c)(2a-3)
11.把下列各式分解因式:
(1)8 m2n+2mn=_____________;
(2)12xyz-9x2y2=_____________;
(3)p(a2 + b2 )- q(a2 + b2 )=_____________;
(4) -x3y3-x2y2-xy=_______________;
2mn(4m+1)
3xy(4z-3xy)
(a2+b2)(p-q)
-xy(x2y2+xy+1)
(5)(x-y)2+y(y-x)=_____________.
(y-x)(2y-x)
(1)6p(p+a)-4a(p+a);
解:原式=2(p+a)(3p-2a)
(2)(x+3)2-(x+3);
解:原式=(x+3)(x+2)
(3)(a-b)3-(b-a)2.
解:原式=(a-b)2(a-b-1)
12 计算
13. 简便计算:
(1) 1.992+1.99×0.01 ; (2)20132+2013-20142;
(3)(-2)101+(-2)100.
(2) 原式=2013(2013+1)-20142
=2013×2014-20142=2014×(2013-2014)
=-2014.
解:(1) 原式=1.99(1.99+0.01)=3.98;
(3)原式=(-2)100 ×(-2+1) =2100 ×(-1)=-2100.
14.(8分)(1)计算:53.6×1.6+18.4×53.6-20×53.6;
解:原式=53.6×(1.6+18.4-20)=0
(2)(黔南州中考)若ab=2,a-b=-1,求代数式a2b-ab2的值.
解:原式=ab(a-b)=-2
15 已知a+b=7,ab=4,求a2b+ab2的值.
∴原式=ab(a+b)=4×7=28.
解:∵a+b=7,ab=4,
方法总结:
含a±b,ab的求值题,通常要将所求代数式进行因式分解,将其变形为能用a±b和ab表示的式子,然后将a±b,ab的值整体带入即可.
二、填空题(每小题3分,共9分)
16.如果把多项式x2-3x+n分解因式得(x-1)(x+m),那么m=_______,n=____.
17.多项式12x3y3z-8x3y2z3+6x4y2z2的公因式是_____________.
18.因式分解:m2-mn+mx-nx=_____________________.
-2
2
2x3y2z
(m-n)(m+x)
解:(1)2x2y+xy2=xy(2x+y)=3 ×4=12.
(2)原式=(2x+1)[(2x+1)-(2x-1)]
=(2x+1)(2x+1-2x+1)=2(2x+1).
19.(1)已知: 2x+y=4,xy=3,求代数式2x2y+xy2的值.
(2)化简求值:(2x+1)2-(2x+1)(2x-1),其中x=0.5 .
将x= 0.5 代入上式,得
原式=4.
三、解答题(共36分)
20.(12分)分解因式:
(1)-27m2n+9mn2-18mn;
解:原式=-9mn(3m-n+2)
(2)x(x-y)(a-b)-y(y-x)(b-a);
解:原式=(x-y)2(a-b)
(3)(a+1)2+(a2+a)2.
解:原式=(a+1)2(1+a2)
(2)已知a,b,c为△ABC的三边,且a2-ab+4ac-4bc=0,试判断△ABC的形状.
解:∵a(a-b)+4c(a-b)=0,∴(a-b)(a+4c)=0,又∵a+4c≠0,∴a-b=0,∴a=b,即△ABC为等腰三角形
解:原式=-2mn(m+n)=1
21.△ABC的三边长分别为a、b、c,且a+2ab=c+2bc,请判断△ABC是等边三角形、等腰三角形还是直角三角形?并说明理由.
拓展提升
∴△ABC是等腰三角形.
解:整理a+2ab=c+2bc得,a+2ab-c-2bc=0,
(a-c)+2b(a-c)=0,(a-c)(1+2b)=0,
∴a-c=0或1+2b=0,
即a=c或b=-0.5(舍去),
【综合运用】
22.(12分)阅读下列因式分解的过程,再回答所提出的问题:
1+x+x(x+1)+x(x+1)2
=(1+x)[1+x+x(1+x)]
=(1+x)2(1+x)
=(1+x)3
(1)上述分解因式的方法是______________法,共应用了____次.
(2)若分解1+x+x(x+1)+x(x+1)2+…+x(x+1)2 019,则需要应用上述方法_______________次,分解因式后的结果是_________________.
提公因式
2
2 019
(1+x)2 020
谢谢观看
