人教版八年级下册数学 18.2.3 正方形 课件 (共26张PPT)
文档属性
| 名称 | 人教版八年级下册数学 18.2.3 正方形 课件 (共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 193.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 20:38:41 | ||
图片预览




文档简介
18.2.3正方形
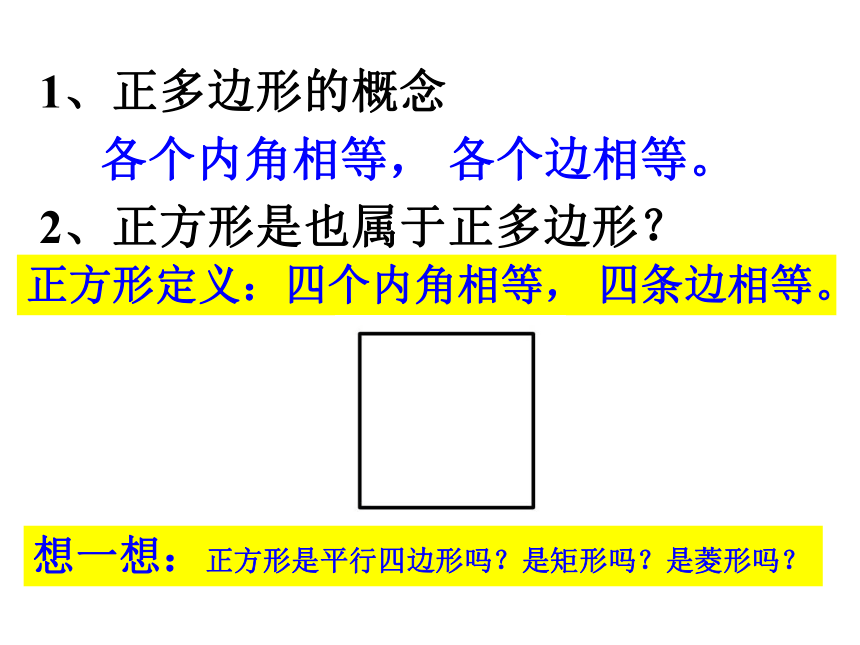
1、正多边形的概念
各个内角相等, 各个边相等。
2、正方形是也属于正多边形?
正方形定义:四个内角相等, 四条边相等。
想一想:正方形是平行四边形吗?是矩形吗?是菱形吗?
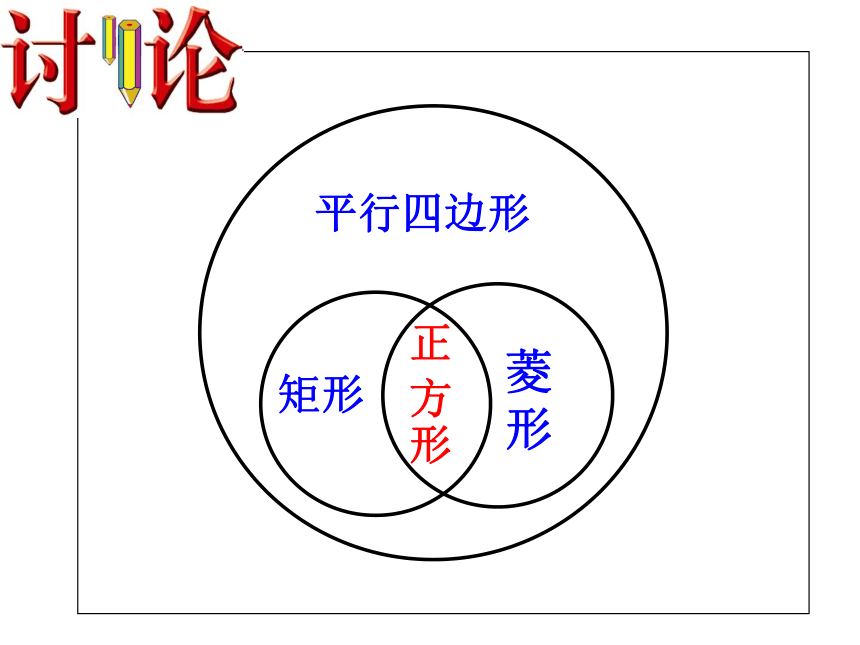
平行四边形,矩形,菱形,正方形的关系!
大家谈
菱形
矩形
平行四边形
正
形
方
小结:
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。
?
正方形的性质=
菱形性质
矩形性质
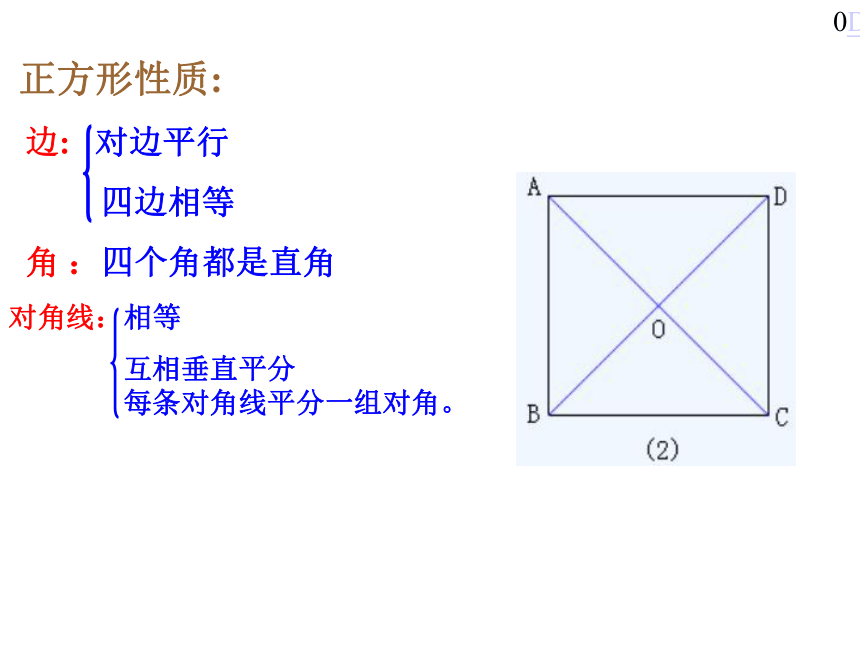
正方形性质:
边: 对边平行
四边相等
角 :四个角都是直角
对角线:相等
互相垂直平分
每条对角线平分一组对角。
0D:\我的文档\左信举\j2040600.swf
范例精讲
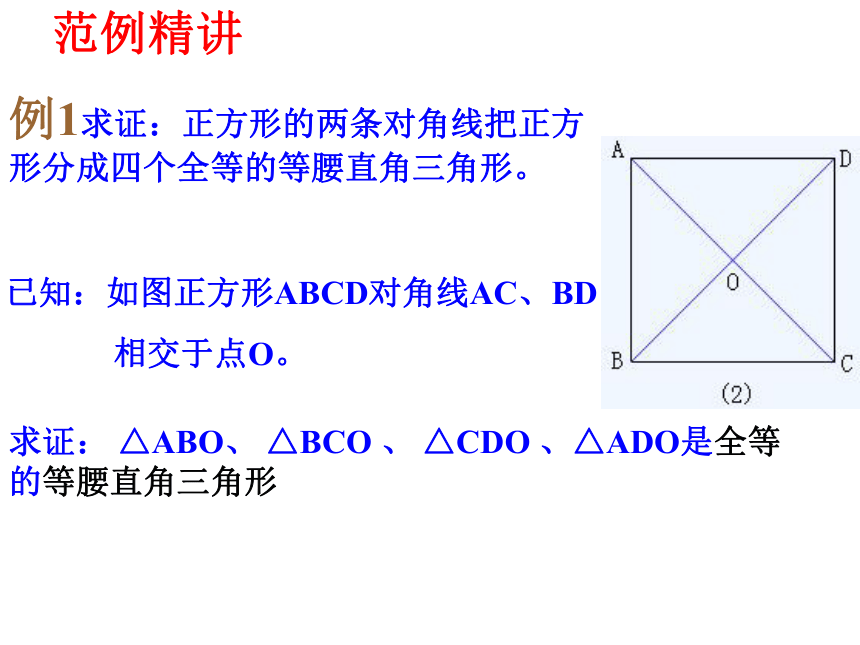
.已知:如图正方形ABCD对角线AC、BD
相
求证: △ABO、 △BCO 、 △CDO 、△ADO是全等的等腰直角三角形
交于点O。
例1求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形。
练习1.
已知:正方形ABCD对角线AC、BD相 交于点O,且AB=a cm,
求:AC的长及正方形的面积S。
练习2.
已知:在正方形ABCD中,对角线AC、
BD相交于点O,且AC=6 cm,
求:正方形的面积S。
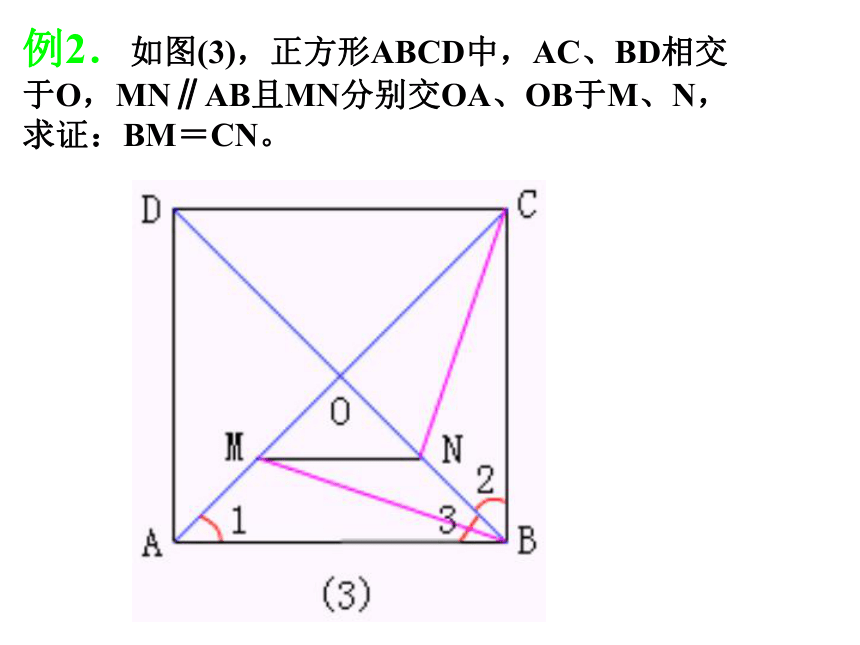
例2.如图(3),正方形ABCD中,AC、BD相交于O,MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。
例3.已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45°
练习1:如图,在正方形ABCD中,点M是对角线BD上的一点,过点M作ME∥CD交BC于点E,作MF∥BC交CD于点F.
求证:AM=EF.
练习2.如图(5),在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。
求证:(1) △ACF≌△DCB
(2) BH⊥AF
例4.如图(6),△ABC的外面作正方形ABDE和ACFG,连结BG、CE,交点为N。求证:∠CEA=∠ABG
证明:∵四边形ABDE和四边形ACFG是正方形。
∴AE=AB AG=AC ∠1=∠2=90°
又∵∠EAC=∠1+∠BAC=90°+∠BAC
∠BAG=∠2+∠BAC=90°+∠BAC
∴∠EAC=∠BAG
∴△AEC≌△ABG (SAS)
∴∠CEA=∠ABG
正方形的判定
1、正多边形的概念
正方形定义:四个内角相等, 四条边相等。
正方形
矩形
实验与观察一:折叠矩形纸片
思考1:当矩形满足条件时,可以成为正方形?
正方形
菱形
实验与观察二:转动菱形模型
思考2:当菱形满足条件时,可以成为正方形?
正方形的第二定义
由正方形的定义可知,
正方形既是有一组邻边相等的矩形,又是 有一个角为直角的菱形。如图(1)。
正方形
2.矩形
有一组邻边相等
3.菱形
有一个角是直角
1.正方形的定义
常
见
说
明
方
法
4、既是矩形又是菱形的四边形为正方形
例1:1、要使一个菱形成为正方形需
增加的条件是
(填上一个条件即可)
2、要使一个矩形成为正方形需添加的条件是
(填上一个条件即可)
例2:下列正确的是
A. 四边相等的四边形是正方形
B.四角相等的四边形是正方形
C.对角线垂直的平行四边形是正方形
D.对角线互相垂直平分且相等的四边形是正方形
1.一个矩形的2条对角线互相垂直,它是正方形吗?
2.一个菱形的2条对角线相等,它是正方形吗?
小试牛刀
思考:
例:在正方形ABCD中,点A`,B`,C`,D`分别在AB,BC,CD,DA上,且AA`=BB`=CC`=DD`.四边形A`B`C`D`是正方形吗?为什么?
D`
C`
B`
A`
D
C
B
A
练习:在△ABC中,AB=AC,D是BC的中点,
DE⊥AB,DF⊥AC,垂足分别是E,F.
1)试说明:DE=DF
2)当△ABC满足什么条件,四边形AEDF是正方形?
思考: 如图,已知□ABCD中,对角线
AC、BD交于点O,E是BD延长线上一点,且
△ACE是等边三角形.
(1)求证:四边形ABCD是菱形;
(2)若∠AEB=2∠EAB,
求证:四边形ABCD是正方形
1、正多边形的概念
各个内角相等, 各个边相等。
2、正方形是也属于正多边形?
正方形定义:四个内角相等, 四条边相等。
想一想:正方形是平行四边形吗?是矩形吗?是菱形吗?
平行四边形,矩形,菱形,正方形的关系!
大家谈
菱形
矩形
平行四边形
正
形
方
小结:
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。
?
正方形的性质=
菱形性质
矩形性质
正方形性质:
边: 对边平行
四边相等
角 :四个角都是直角
对角线:相等
互相垂直平分
每条对角线平分一组对角。
0D:\我的文档\左信举\j2040600.swf
范例精讲
.已知:如图正方形ABCD对角线AC、BD
相
求证: △ABO、 △BCO 、 △CDO 、△ADO是全等的等腰直角三角形
交于点O。
例1求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形。
练习1.
已知:正方形ABCD对角线AC、BD相 交于点O,且AB=a cm,
求:AC的长及正方形的面积S。
练习2.
已知:在正方形ABCD中,对角线AC、
BD相交于点O,且AC=6 cm,
求:正方形的面积S。
例2.如图(3),正方形ABCD中,AC、BD相交于O,MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。
例3.已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45°
练习1:如图,在正方形ABCD中,点M是对角线BD上的一点,过点M作ME∥CD交BC于点E,作MF∥BC交CD于点F.
求证:AM=EF.
练习2.如图(5),在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。
求证:(1) △ACF≌△DCB
(2) BH⊥AF
例4.如图(6),△ABC的外面作正方形ABDE和ACFG,连结BG、CE,交点为N。求证:∠CEA=∠ABG
证明:∵四边形ABDE和四边形ACFG是正方形。
∴AE=AB AG=AC ∠1=∠2=90°
又∵∠EAC=∠1+∠BAC=90°+∠BAC
∠BAG=∠2+∠BAC=90°+∠BAC
∴∠EAC=∠BAG
∴△AEC≌△ABG (SAS)
∴∠CEA=∠ABG
正方形的判定
1、正多边形的概念
正方形定义:四个内角相等, 四条边相等。
正方形
矩形
实验与观察一:折叠矩形纸片
思考1:当矩形满足条件时,可以成为正方形?
正方形
菱形
实验与观察二:转动菱形模型
思考2:当菱形满足条件时,可以成为正方形?
正方形的第二定义
由正方形的定义可知,
正方形既是有一组邻边相等的矩形,又是 有一个角为直角的菱形。如图(1)。
正方形
2.矩形
有一组邻边相等
3.菱形
有一个角是直角
1.正方形的定义
常
见
说
明
方
法
4、既是矩形又是菱形的四边形为正方形
例1:1、要使一个菱形成为正方形需
增加的条件是
(填上一个条件即可)
2、要使一个矩形成为正方形需添加的条件是
(填上一个条件即可)
例2:下列正确的是
A. 四边相等的四边形是正方形
B.四角相等的四边形是正方形
C.对角线垂直的平行四边形是正方形
D.对角线互相垂直平分且相等的四边形是正方形
1.一个矩形的2条对角线互相垂直,它是正方形吗?
2.一个菱形的2条对角线相等,它是正方形吗?
小试牛刀
思考:
例:在正方形ABCD中,点A`,B`,C`,D`分别在AB,BC,CD,DA上,且AA`=BB`=CC`=DD`.四边形A`B`C`D`是正方形吗?为什么?
D`
C`
B`
A`
D
C
B
A
练习:在△ABC中,AB=AC,D是BC的中点,
DE⊥AB,DF⊥AC,垂足分别是E,F.
1)试说明:DE=DF
2)当△ABC满足什么条件,四边形AEDF是正方形?
思考: 如图,已知□ABCD中,对角线
AC、BD交于点O,E是BD延长线上一点,且
△ACE是等边三角形.
(1)求证:四边形ABCD是菱形;
(2)若∠AEB=2∠EAB,
求证:四边形ABCD是正方形
