人教版八年级下册数学课件:19.2.1 正比例函数的图象与性质(共16张PPT)
文档属性
| 名称 | 人教版八年级下册数学课件:19.2.1 正比例函数的图象与性质(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 603.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:00:00 | ||
图片预览





文档简介
19.2.1 正比例函数
第十九章 一次函数
第2课时 正比例函数的图象和性质
1.函数=常数x自变量
2.自变量x的指数是1
3.比例系数k≠0
温故知新
问题1.什么是正比例函数?
一般地,形如 y=kx(k为常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数。
温故知新
列表
描点
连线
问题2:描点法画函数图象的步骤是:
、 、 、 。
①③⑤⑦
问:在下列函数中,哪些是正比例函数?并指出正比例系数分别是多少.
①y=x ②y=3x2 ③y= -x ④y=2x-4,
⑤y=2x ⑥ ⑦y=-2x ⑧y=kx
写解析式
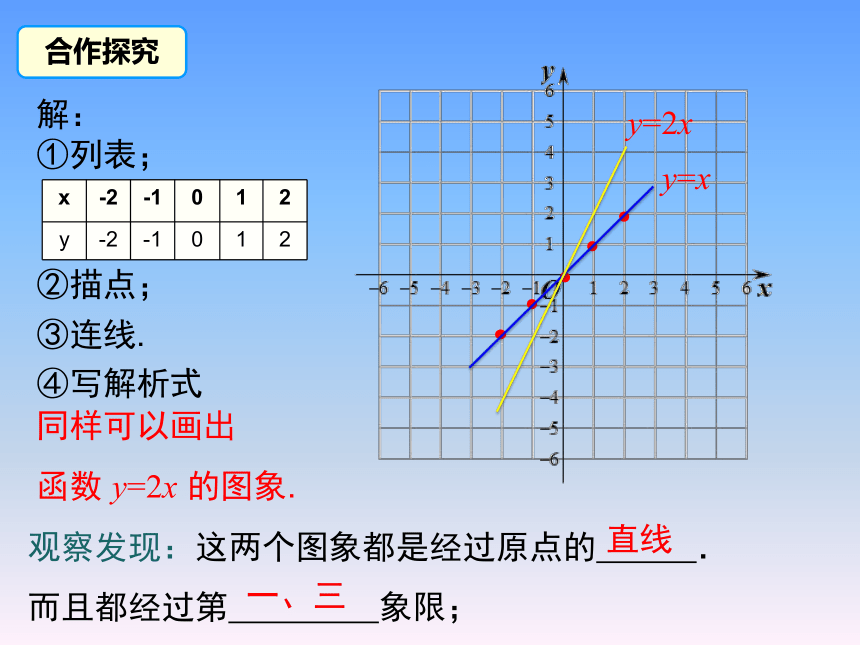
活动一:画出下列正比例函数的图象:
(1)y=x,y=2x (2)y=-x,y=-2x.
提示:一般地,非实际问题中正比例函数的自变量取任意实数
合作探究
②描点;
③连线.
同样可以画出
函数 y=2x 的图象.
观察发现:这两个图象都是经过原点的 .
而且都经过第 象限;
一、三
直线
解:
①列表;
x
-2
-1
0
1
2
y
-2
-1
0
1
2
y=x
y=2x
合作探究
④写解析式
合作探究
活动二:通过以上图象,思考下列问题
1.经过原点和点(1,k)(k是常数,k≠0)的直线是哪个函数的图象?
2.画正比例函数的图象时,怎样画最简单?为什么?
正比例函数y=kx(k≠0)的图象过点(0,0)和(1,k)的直线,因此,过点(0,0)和(1,k)的直线就是正比例函数y=kx(k≠0)的图象。
正比例函数
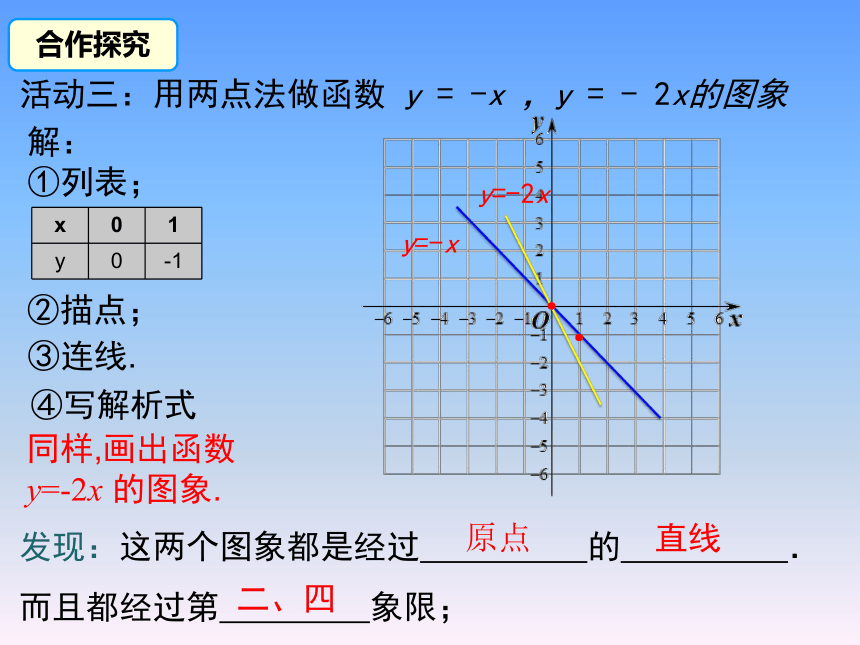
发现:这两个图象都是经过 的 .
而且都经过第 象限;
二、四
活动三:用两点法做函数 y = -x ,y = - 2x的图象
合作探究
解:
①列表;
x
0
1
y
0
-1
·
·
②描点;
③连线.
同样,画出函数 y=-2x 的图象.
直线
原点
y=-x
y=-2x
④写解析式
对比观察四个函数的图象,它们有哪些相同点和不同点?比如图象形状、象限、函数的增减性
要点归纳
另外:函数y=kx 的图象我们也称作直线y=kx
y=kx(k≠0)
图象形状
一条经过原点(0,0)和(1,k)的直线
k>0
k<0
函数图象
经过的象限
一、三象限
二、四象限
增减性
y随x增大而增大
y随x增大而减小
k越大直线越靠近y轴
k越小直线越靠近y轴
例1 已知正比例函数y=mx的图象经过点(m,4),且y的值随着x值的增大而减小,求m的值.
解:∵正比例函数y=mx的图象经过点(m,4),
∴4=m·m,解得m=±2.
又∵y的值随着x值的增大而减小,
∴m<0,故m=-2
精讲实练
1.函数y=-7x的图象经过第_________象限,经过点_______与点 ,y随x的增大而_______.
2.已知正比例函数y=(2m+4)x.
(1)当m ,函数图象经过第一、三象限;
(2)当m ,y 随x 的增大而减小;
(3)当m ,函数图象经过点(2,10)
牛刀小试
二、四
(0,0)
(1,-7)
减小
>-2
<-2
=0.5
例2.如图分别是函数y=k1 x,y=k2 x,y=k3 x,y=k4 x的图象.(1)k1 k2,k3 k4(填“>”或“<”或“=”);
(2)用不等号将k1, k2, k3, k4及0依次连接起来.
<
解: k1<k2 <0<k3 <k4
4
2
-2
-4
4
x
y
O
y =k4 x
-4
-2
2
y =k3 x
y =k2 x
y =k1 x
<
精讲实练
课堂检测
1.已知正比例函数y=2x的图象上有两点(3,y1),
(5,y2),则y1 y2.
<
2.已知正比例函数y=kx(k<0)的图象上有两点(-3,y1),
(1,y2),则y1 y2.
>
正比例函数的图象和性质
图象:
经过原点的直线.
当k>0时,经过第一、三象限;当k<0时,经过第二、四象限.
性质:
当k>0时,y的值随x值的增大而增大;
当k<0时,y的值随x值的增大而减小.
课堂小结
伟大的成功和辛勤的劳动是成正比例关系的,一分劳动就会有一分收获,日积月累,积少成多,奇迹就可以创造出来。
---------鲁迅
寄 语
再见
第十九章 一次函数
第2课时 正比例函数的图象和性质
1.函数=常数x自变量
2.自变量x的指数是1
3.比例系数k≠0
温故知新
问题1.什么是正比例函数?
一般地,形如 y=kx(k为常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数。
温故知新
列表
描点
连线
问题2:描点法画函数图象的步骤是:
、 、 、 。
①③⑤⑦
问:在下列函数中,哪些是正比例函数?并指出正比例系数分别是多少.
①y=x ②y=3x2 ③y= -x ④y=2x-4,
⑤y=2x ⑥ ⑦y=-2x ⑧y=kx
写解析式
活动一:画出下列正比例函数的图象:
(1)y=x,y=2x (2)y=-x,y=-2x.
提示:一般地,非实际问题中正比例函数的自变量取任意实数
合作探究
②描点;
③连线.
同样可以画出
函数 y=2x 的图象.
观察发现:这两个图象都是经过原点的 .
而且都经过第 象限;
一、三
直线
解:
①列表;
x
-2
-1
0
1
2
y
-2
-1
0
1
2
y=x
y=2x
合作探究
④写解析式
合作探究
活动二:通过以上图象,思考下列问题
1.经过原点和点(1,k)(k是常数,k≠0)的直线是哪个函数的图象?
2.画正比例函数的图象时,怎样画最简单?为什么?
正比例函数y=kx(k≠0)的图象过点(0,0)和(1,k)的直线,因此,过点(0,0)和(1,k)的直线就是正比例函数y=kx(k≠0)的图象。
正比例函数
发现:这两个图象都是经过 的 .
而且都经过第 象限;
二、四
活动三:用两点法做函数 y = -x ,y = - 2x的图象
合作探究
解:
①列表;
x
0
1
y
0
-1
·
·
②描点;
③连线.
同样,画出函数 y=-2x 的图象.
直线
原点
y=-x
y=-2x
④写解析式
对比观察四个函数的图象,它们有哪些相同点和不同点?比如图象形状、象限、函数的增减性
要点归纳
另外:函数y=kx 的图象我们也称作直线y=kx
y=kx(k≠0)
图象形状
一条经过原点(0,0)和(1,k)的直线
k>0
k<0
函数图象
经过的象限
一、三象限
二、四象限
增减性
y随x增大而增大
y随x增大而减小
k越大直线越靠近y轴
k越小直线越靠近y轴
例1 已知正比例函数y=mx的图象经过点(m,4),且y的值随着x值的增大而减小,求m的值.
解:∵正比例函数y=mx的图象经过点(m,4),
∴4=m·m,解得m=±2.
又∵y的值随着x值的增大而减小,
∴m<0,故m=-2
精讲实练
1.函数y=-7x的图象经过第_________象限,经过点_______与点 ,y随x的增大而_______.
2.已知正比例函数y=(2m+4)x.
(1)当m ,函数图象经过第一、三象限;
(2)当m ,y 随x 的增大而减小;
(3)当m ,函数图象经过点(2,10)
牛刀小试
二、四
(0,0)
(1,-7)
减小
>-2
<-2
=0.5
例2.如图分别是函数y=k1 x,y=k2 x,y=k3 x,y=k4 x的图象.(1)k1 k2,k3 k4(填“>”或“<”或“=”);
(2)用不等号将k1, k2, k3, k4及0依次连接起来.
<
解: k1<k2 <0<k3 <k4
4
2
-2
-4
4
x
y
O
y =k4 x
-4
-2
2
y =k3 x
y =k2 x
y =k1 x
<
精讲实练
课堂检测
1.已知正比例函数y=2x的图象上有两点(3,y1),
(5,y2),则y1 y2.
<
2.已知正比例函数y=kx(k<0)的图象上有两点(-3,y1),
(1,y2),则y1 y2.
>
正比例函数的图象和性质
图象:
经过原点的直线.
当k>0时,经过第一、三象限;当k<0时,经过第二、四象限.
性质:
当k>0时,y的值随x值的增大而增大;
当k<0时,y的值随x值的增大而减小.
课堂小结
伟大的成功和辛勤的劳动是成正比例关系的,一分劳动就会有一分收获,日积月累,积少成多,奇迹就可以创造出来。
---------鲁迅
寄 语
再见
