人教版八年级下册数学课件:19.2.2一次函数(共19张PPT)
文档属性
| 名称 | 人教版八年级下册数学课件:19.2.2一次函数(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 457.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:00:00 | ||
图片预览






文档简介
一次函数
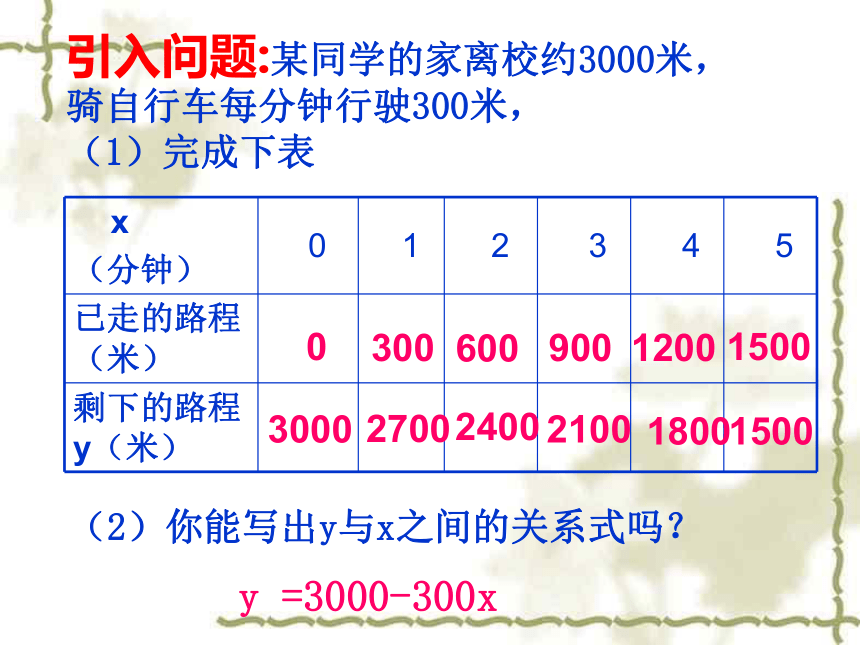
引入问题:某同学的家离校约3000米,骑自行车每分钟行驶300米,
(1)完成下表
x
(分钟)
0
1
2
3
4
5
已走的路程(米)
剩下的路程 y(米)
(2)你能写出y与x之间的关系式吗?
y =3000-300x
3000
2700
2400
2100
1800
1500
0
300
600
900
1200
1500
小明暑假第一次去北京.汽车驶上A地的高速公路后,小明观察里程碑,发现汽车的平均速度是95千米/时.已知A地直达北京的高速公路全程570千米,小明想知道汽车从A地驶出后,距北京的路程和汽车在高速公路上行驶的时间有什么关系,以便根据时间估计自己和北京的距离.
问题1
分 析
我们知道汽车距北京的路程随着行车时间而变化.要想找出这两个变化着的量的关系,并据此得出相应的值,显然,应该探究这两个量之间的变化规律.为此,我们设汽车在高速公路上行驶时间为t小时,汽车距北京的路程为s千米,则不难得到s与t的函数关系式是
s=570-95t (1)
问题2
小张准备将平时的零用钱节约一些储存起来.他已存有50元,从现在起每个月节存12元.试写出小张的存款数与从现在开始的月份数之间的函数关系式.
分 析
同样,我们设从现在开始的月份数为x,小张的存款数为y元,得到所求的函数关系式为
y=_______________ (2)
50+12x
概 括
上述函数的解析式都是用自变量的一次整式表示的,我们称它们为一次函数.
一次函数通常可以表示为y=kx+b的形式,其中k、b是常数,k≠0.
特别地,当b=0时,一次函数y=kx(常数k≠0)也叫做正比例函数.
正比例函数是一种特殊的一次函数.
一次函数定义
它是一次函数.
它不是一次函数.
它是一次函数,也是正比例函数.
它是一次函数.
它不是一次函数.
它是一次函数.
下列函数中,哪些是一次函数,并指出K、b
(1) y =-3X+7
(2) y =6X2-3X
(3) y =8X
(4) y =1+9X
(5) y =
(6)y = -0.5x-1
巩固概念
1.已知下列函数:y=2x+1;
;s=60t;y=100-25x,其中表示
一次函数的有( )
(A )1个
( B)2个
( C)3个
( D)4个
D
2.要使y=(m-2)xn-1+n是关于x的一次函数,n,m应满足 , .
n=2
m≠2
3.下列说法不正确的是( )
(A)一次函数不一定是正比例函数
(B)不是一次函数就一定不是正比例函数
(C)正比例函数是特定的一次函数
(D)不是正比例函数就不是一次函数
D
4.若函数y=(m-1)x|m|+m是关于x的一次函数,试求m的值.
1.已知函数y=(m+1)x+(m2-1),当m取什么值时, y是x的一次函数?当m取什么值时,y是x的正比例函数?
应用拓展
解:(1)因为y是x的一次函数
所以 m+1 ≠ 0 m≠-1
(2)因为y是x的正比例函数
所以 m2-1=0 m=1或-1
又因为 m≠ -1 所以 m=1
2.已知函数y=(k-2)x+2k+1,若它是一次函数,求k的取值范围;若它是正比例函数,求k的值.
解:
若y=(k-2)x+2k+1是正比例函数
则
k=-
1
2
2k+1=0,
k-2≠0,
解得
若y=(k-2)x+2k+1是一次函数
则k-2≠0,
即k ≠ 2
3.已知y与x-3成正比例,当x=4时, y=3 .
(1)写出y与x之间的函数关系式;
(2) y与x之间是什么函数关系式;
(3)求x =2.5时, y的值
解:
(1) ∵ y与x-3成正比例
∴可设y = k(x-3)
又∵当x=4时, y=3
∴3 = k(4-3)
解得k =3
∴y = 3(x-3) = 3x-9
(2) y是x的一次函数;
(3)当x =2.5时, y = 3×2.5-9 =-1.5
(k ≠ 0)
某书定价25元,如果一次购买20本以上,超过20本的部分打八折,试写出付款金额y(单位:元)与购书数量x(单位:本)之间的函数关系 .
某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费,月用电量不超过200度时,按0.55元/度计费;月用电量超过200度时,其中的200度仍按0.55元/度计费,超过部分按0.70元/度计费,设每户家庭月用电量为x度时,应交电费y元
(1)分别求出0≤x≤200和x>200时,y与x的函数表达式;
(2)小明家5月份交纳电费117元,小明家这个月用电多少度?
如图在矩形ABCD中,AD=8cm,AB=6cm.点A处有一动点E以1cm∕s的速度由点A向点B运动,同时点C处也有一动点F以2cm∕s的速度由点C向点D运动?设运动的时间为x(s)四边形EBFD的面积为y(cm2)求y与x的函数关系式及自变量x的取值范围.
4.已知A、B两地相距30千米, B 、C两地相距48千米,某人骑自行车以每小时12千米的速度从A地出发,经过B地到达C地.设此人骑车时间为x(时)离B地距离为y(千米).
(1)当此人在A、B两地之间时,求 y与x之间的函数关系式及自变量x的取值范围;
(2)当此人在B 、C两地之间时,求 y与x之间的函数关系式及自变量x的取值范围;
(1) y=30-12x,
(0≤x ≤2.5)
(2) y=12x -30,
(2.5≤x ≤6.5)
略解:
分析:
5.某油库有一没储油的储油罐,在开始的8分钟内,只开进油管,不开出油管,油罐进油至24吨后,将进油管和出油管同时打开16分钟,油罐中的油从24吨增至40吨.随后又关闭进油管,只开出油管,直至将油罐内的油放完.假设在单位时间内进油管与出油管的流量分别保持不变.写出这段时间内油罐的储油量y(吨)与进出油时间x(分)的函数式及相应的x取值范围.
(1)在第一阶段:
(0≤x ≤8)
24÷8=3
解:
分析:
∴ y= 3x
(0≤x ≤8)
5.某油库有一没储油的储油罐,在开始的8分钟内,只开进油管,不开出油管,油罐进油至24吨后,将进油管和出油管同时打开16分钟,油罐中的油从24吨增至40吨.随后又关闭进油管,只开出油管,直至将油罐内的油放完.假设在单位时间内进油管与出油管的流量分别保持不变.写出这段时间内油罐的储油量y(吨)与进出油时间x(分)的函数式及相应的x取值范围.
(2)在第二阶段:
(8≤x ≤8+16)
设每分钟放出油m吨,
解:
∴ y= 24+(3-2)(x-8)
(8≤x ≤24)
则
16×3-16m =40-24
m =2
即 y= 16+x
5.某油库有一没储油的储油罐,在开始的8分钟内,只开进油管,不开出油管,油罐进油至24吨后,将进油管和出油管同时打开16分钟,油罐中的油从24吨增至40吨.随后又关闭进油管,只开出油管,直至将油罐内的油放完.假设在单位时间内进油管与出油管的流量分别保持不变.写出这段时间内油罐的储油量y(吨)与进出油时间x(分)的函数式及相应的x取值范围.
(3)在第三阶段:
40÷2=20
解:
∴ y= 40-2(x-24)
(24≤x ≤44)
24+20 =44
即 y=-2x +88
小结
函数的解析式是用自变量的一次整式表示的,我们称它们为一次函数.
一次函数通常可以表示为y=kx+b的形式,其中k、b是常数,k≠0.
正比例函数也是一次函数,它是一次函数的特例.
特别地,当b=0时,一次函数y=kx(常数k≠0)也叫做正比例函数.
引入问题:某同学的家离校约3000米,骑自行车每分钟行驶300米,
(1)完成下表
x
(分钟)
0
1
2
3
4
5
已走的路程(米)
剩下的路程 y(米)
(2)你能写出y与x之间的关系式吗?
y =3000-300x
3000
2700
2400
2100
1800
1500
0
300
600
900
1200
1500
小明暑假第一次去北京.汽车驶上A地的高速公路后,小明观察里程碑,发现汽车的平均速度是95千米/时.已知A地直达北京的高速公路全程570千米,小明想知道汽车从A地驶出后,距北京的路程和汽车在高速公路上行驶的时间有什么关系,以便根据时间估计自己和北京的距离.
问题1
分 析
我们知道汽车距北京的路程随着行车时间而变化.要想找出这两个变化着的量的关系,并据此得出相应的值,显然,应该探究这两个量之间的变化规律.为此,我们设汽车在高速公路上行驶时间为t小时,汽车距北京的路程为s千米,则不难得到s与t的函数关系式是
s=570-95t (1)
问题2
小张准备将平时的零用钱节约一些储存起来.他已存有50元,从现在起每个月节存12元.试写出小张的存款数与从现在开始的月份数之间的函数关系式.
分 析
同样,我们设从现在开始的月份数为x,小张的存款数为y元,得到所求的函数关系式为
y=_______________ (2)
50+12x
概 括
上述函数的解析式都是用自变量的一次整式表示的,我们称它们为一次函数.
一次函数通常可以表示为y=kx+b的形式,其中k、b是常数,k≠0.
特别地,当b=0时,一次函数y=kx(常数k≠0)也叫做正比例函数.
正比例函数是一种特殊的一次函数.
一次函数定义
它是一次函数.
它不是一次函数.
它是一次函数,也是正比例函数.
它是一次函数.
它不是一次函数.
它是一次函数.
下列函数中,哪些是一次函数,并指出K、b
(1) y =-3X+7
(2) y =6X2-3X
(3) y =8X
(4) y =1+9X
(5) y =
(6)y = -0.5x-1
巩固概念
1.已知下列函数:y=2x+1;
;s=60t;y=100-25x,其中表示
一次函数的有( )
(A )1个
( B)2个
( C)3个
( D)4个
D
2.要使y=(m-2)xn-1+n是关于x的一次函数,n,m应满足 , .
n=2
m≠2
3.下列说法不正确的是( )
(A)一次函数不一定是正比例函数
(B)不是一次函数就一定不是正比例函数
(C)正比例函数是特定的一次函数
(D)不是正比例函数就不是一次函数
D
4.若函数y=(m-1)x|m|+m是关于x的一次函数,试求m的值.
1.已知函数y=(m+1)x+(m2-1),当m取什么值时, y是x的一次函数?当m取什么值时,y是x的正比例函数?
应用拓展
解:(1)因为y是x的一次函数
所以 m+1 ≠ 0 m≠-1
(2)因为y是x的正比例函数
所以 m2-1=0 m=1或-1
又因为 m≠ -1 所以 m=1
2.已知函数y=(k-2)x+2k+1,若它是一次函数,求k的取值范围;若它是正比例函数,求k的值.
解:
若y=(k-2)x+2k+1是正比例函数
则
k=-
1
2
2k+1=0,
k-2≠0,
解得
若y=(k-2)x+2k+1是一次函数
则k-2≠0,
即k ≠ 2
3.已知y与x-3成正比例,当x=4时, y=3 .
(1)写出y与x之间的函数关系式;
(2) y与x之间是什么函数关系式;
(3)求x =2.5时, y的值
解:
(1) ∵ y与x-3成正比例
∴可设y = k(x-3)
又∵当x=4时, y=3
∴3 = k(4-3)
解得k =3
∴y = 3(x-3) = 3x-9
(2) y是x的一次函数;
(3)当x =2.5时, y = 3×2.5-9 =-1.5
(k ≠ 0)
某书定价25元,如果一次购买20本以上,超过20本的部分打八折,试写出付款金额y(单位:元)与购书数量x(单位:本)之间的函数关系 .
某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费,月用电量不超过200度时,按0.55元/度计费;月用电量超过200度时,其中的200度仍按0.55元/度计费,超过部分按0.70元/度计费,设每户家庭月用电量为x度时,应交电费y元
(1)分别求出0≤x≤200和x>200时,y与x的函数表达式;
(2)小明家5月份交纳电费117元,小明家这个月用电多少度?
如图在矩形ABCD中,AD=8cm,AB=6cm.点A处有一动点E以1cm∕s的速度由点A向点B运动,同时点C处也有一动点F以2cm∕s的速度由点C向点D运动?设运动的时间为x(s)四边形EBFD的面积为y(cm2)求y与x的函数关系式及自变量x的取值范围.
4.已知A、B两地相距30千米, B 、C两地相距48千米,某人骑自行车以每小时12千米的速度从A地出发,经过B地到达C地.设此人骑车时间为x(时)离B地距离为y(千米).
(1)当此人在A、B两地之间时,求 y与x之间的函数关系式及自变量x的取值范围;
(2)当此人在B 、C两地之间时,求 y与x之间的函数关系式及自变量x的取值范围;
(1) y=30-12x,
(0≤x ≤2.5)
(2) y=12x -30,
(2.5≤x ≤6.5)
略解:
分析:
5.某油库有一没储油的储油罐,在开始的8分钟内,只开进油管,不开出油管,油罐进油至24吨后,将进油管和出油管同时打开16分钟,油罐中的油从24吨增至40吨.随后又关闭进油管,只开出油管,直至将油罐内的油放完.假设在单位时间内进油管与出油管的流量分别保持不变.写出这段时间内油罐的储油量y(吨)与进出油时间x(分)的函数式及相应的x取值范围.
(1)在第一阶段:
(0≤x ≤8)
24÷8=3
解:
分析:
∴ y= 3x
(0≤x ≤8)
5.某油库有一没储油的储油罐,在开始的8分钟内,只开进油管,不开出油管,油罐进油至24吨后,将进油管和出油管同时打开16分钟,油罐中的油从24吨增至40吨.随后又关闭进油管,只开出油管,直至将油罐内的油放完.假设在单位时间内进油管与出油管的流量分别保持不变.写出这段时间内油罐的储油量y(吨)与进出油时间x(分)的函数式及相应的x取值范围.
(2)在第二阶段:
(8≤x ≤8+16)
设每分钟放出油m吨,
解:
∴ y= 24+(3-2)(x-8)
(8≤x ≤24)
则
16×3-16m =40-24
m =2
即 y= 16+x
5.某油库有一没储油的储油罐,在开始的8分钟内,只开进油管,不开出油管,油罐进油至24吨后,将进油管和出油管同时打开16分钟,油罐中的油从24吨增至40吨.随后又关闭进油管,只开出油管,直至将油罐内的油放完.假设在单位时间内进油管与出油管的流量分别保持不变.写出这段时间内油罐的储油量y(吨)与进出油时间x(分)的函数式及相应的x取值范围.
(3)在第三阶段:
40÷2=20
解:
∴ y= 40-2(x-24)
(24≤x ≤44)
24+20 =44
即 y=-2x +88
小结
函数的解析式是用自变量的一次整式表示的,我们称它们为一次函数.
一次函数通常可以表示为y=kx+b的形式,其中k、b是常数,k≠0.
正比例函数也是一次函数,它是一次函数的特例.
特别地,当b=0时,一次函数y=kx(常数k≠0)也叫做正比例函数.
