人教版七年级数学 3.2 合并同类项与移项 课件
文档属性
| 名称 | 人教版七年级数学 3.2 合并同类项与移项 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 871.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 00:00:00 | ||
图片预览






文档简介
3.2 解一元一次方程(一)
义务教育教科书 数学 七年级 上册
理解移项法则,会解形如ax+b=cx+d的方程。
学习目标
能够从实际问题列出一元一次方程,进一步体会方程模型思想的作用及应用价值。
回顾旧知
用合并同类项进行化简
:
1. 20x -12x= ________
2. x + 7x-5x= ________
3. ________
4. 3y-4y-(-2y)=_______
8x
3x
-y
y
合并同类项的法则:
同类项的系数相加所得的结果作为系数,字母和字母的指数
不变.
当天平处于平衡状态时,你能由图列出一个一元一次方程吗?
问题1:
某校三年共购买计算机140台,去年购买数量是前年的2倍,今年购买数量又是去年的2倍.前年这个学校购买了多少台计算机?
分析:
设前年这个学校购买了计算机x台,则去年购买计算机_____台,今年购买计算机_____台,
根据问题中的相等关系:
前年购买量+去年购买量+今年购买量=140台
列得方程
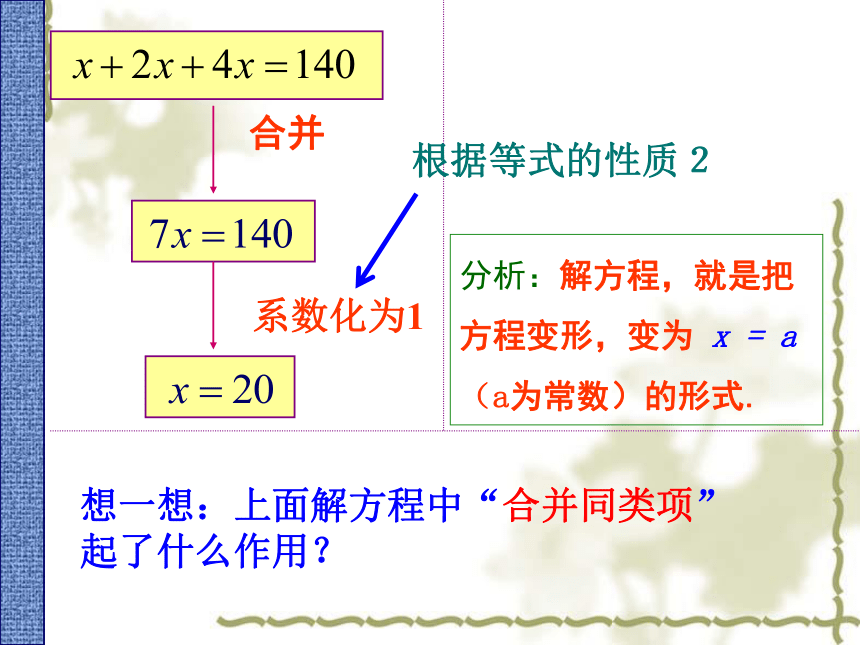
x + 2x +4x = 140
2x
4x
思考:怎样解这个方程呢?
分析:解方程,就是把方程变形,变为 x = a(a为常数)的形式.
合并
系数化为1
想一想:上面解方程中“合并同类项”起了什么作用?
根据等式的性质2
合并同类项起到了“化简”的作用,即把含有未知数的项合并,从而把方程转化为ax=b,使其更接近x=a的形式(其中a,b是常数) .
合并同类项的作用:
解方程:
解:
合并同类项,得
(1) x+2x=14
x=14
系数化为1,得
x=4:
(2) 7x-2.5x+3x-1.5x=-15×4-6×3
解:
合并同类项,得
系数化为1,得
6x=-78
x=-13
解下列方程
你一定会!
小试牛刀
1、设未知数:设这个班有x名学生.
2、找等量关系
这批书的总数是一个定值,表示它的两个等式相等
3、列方程
3x+20 = 4x-25
分析问题
把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?
每人分3本,共分出3x本,加上剩余的20本,这批书共 本.
每人分4本,需要____ 本,减去缺的25本,
这批书共 本.
(3x+20)
4x
(4x-25)
3x+20=4x-25
3x+20-20=4x-25-20
提问2:如何才能使这个方程向x=a的形式转化?
将原方程转化成了x=a的形式。
3x=4x-25-20
3x-4x=4x-4x-25-20
3x-4x=-25-20
你发现了什么?
3x +20 = 4x -25
3x-4x=-25 -20
把等式一边的某一项改变符号后移到另一边,叫做移项.
跨等号就变号!
3x+20=4x-25
3x-4x=-25-20
-x=-45
X=45
移项
合并同类项
系数化为1
下面的框图表示了解这个方程的具体过程:
3x+20=4x-2x
解:移项 3x+2x=32-7
合并同类项 5x=25
系数化为1 x=5
例1:解下列方程
解:移项,得
系数化为1,得 x = - 2
(2)
解:移项,得
合并同类项,得
系数化为1,得
(1)
运用新知
含未知数的项宜向左移、
常数项往右移.
左边对含未知数的项合并、
右边对常数项合并.
移项
移项
练习1:判断下列移项是否正确:
随堂练习
解下列方程:
x+7=0;
x —10 =-3;
(3) 3x=-2x-6;
(4)0.2x+1.8=3-1.8x.
练习1
解下列方程:
(1)3(x-1)=9;
(2)8(y-3)=5y+3;
(3)-7(x+4)-5=2(x-3);
(4)3(x-1)+2=2(x+3)+7.
练习2
1. :一般地,把方程中的某些项改变符号后,从方程的一边移到另一边,这种变形叫做移项。
3.移项要改变符号.
2.解一元一次方程需要移项时我们把含未知数的项移到方程的一边(通常移到左边),常数项移到方程的另一边(通常移到右边).
这节课我们学习了什么?
移项
义务教育教科书 数学 七年级 上册
理解移项法则,会解形如ax+b=cx+d的方程。
学习目标
能够从实际问题列出一元一次方程,进一步体会方程模型思想的作用及应用价值。
回顾旧知
用合并同类项进行化简
:
1. 20x -12x= ________
2. x + 7x-5x= ________
3. ________
4. 3y-4y-(-2y)=_______
8x
3x
-y
y
合并同类项的法则:
同类项的系数相加所得的结果作为系数,字母和字母的指数
不变.
当天平处于平衡状态时,你能由图列出一个一元一次方程吗?
问题1:
某校三年共购买计算机140台,去年购买数量是前年的2倍,今年购买数量又是去年的2倍.前年这个学校购买了多少台计算机?
分析:
设前年这个学校购买了计算机x台,则去年购买计算机_____台,今年购买计算机_____台,
根据问题中的相等关系:
前年购买量+去年购买量+今年购买量=140台
列得方程
x + 2x +4x = 140
2x
4x
思考:怎样解这个方程呢?
分析:解方程,就是把方程变形,变为 x = a(a为常数)的形式.
合并
系数化为1
想一想:上面解方程中“合并同类项”起了什么作用?
根据等式的性质2
合并同类项起到了“化简”的作用,即把含有未知数的项合并,从而把方程转化为ax=b,使其更接近x=a的形式(其中a,b是常数) .
合并同类项的作用:
解方程:
解:
合并同类项,得
(1) x+2x=14
x=14
系数化为1,得
x=4:
(2) 7x-2.5x+3x-1.5x=-15×4-6×3
解:
合并同类项,得
系数化为1,得
6x=-78
x=-13
解下列方程
你一定会!
小试牛刀
1、设未知数:设这个班有x名学生.
2、找等量关系
这批书的总数是一个定值,表示它的两个等式相等
3、列方程
3x+20 = 4x-25
分析问题
把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?
每人分3本,共分出3x本,加上剩余的20本,这批书共 本.
每人分4本,需要____ 本,减去缺的25本,
这批书共 本.
(3x+20)
4x
(4x-25)
3x+20=4x-25
3x+20-20=4x-25-20
提问2:如何才能使这个方程向x=a的形式转化?
将原方程转化成了x=a的形式。
3x=4x-25-20
3x-4x=4x-4x-25-20
3x-4x=-25-20
你发现了什么?
3x +20 = 4x -25
3x-4x=-25 -20
把等式一边的某一项改变符号后移到另一边,叫做移项.
跨等号就变号!
3x+20=4x-25
3x-4x=-25-20
-x=-45
X=45
移项
合并同类项
系数化为1
下面的框图表示了解这个方程的具体过程:
3x+20=4x-2x
解:移项 3x+2x=32-7
合并同类项 5x=25
系数化为1 x=5
例1:解下列方程
解:移项,得
系数化为1,得 x = - 2
(2)
解:移项,得
合并同类项,得
系数化为1,得
(1)
运用新知
含未知数的项宜向左移、
常数项往右移.
左边对含未知数的项合并、
右边对常数项合并.
移项
移项
练习1:判断下列移项是否正确:
随堂练习
解下列方程:
x+7=0;
x —10 =-3;
(3) 3x=-2x-6;
(4)0.2x+1.8=3-1.8x.
练习1
解下列方程:
(1)3(x-1)=9;
(2)8(y-3)=5y+3;
(3)-7(x+4)-5=2(x-3);
(4)3(x-1)+2=2(x+3)+7.
练习2
1. :一般地,把方程中的某些项改变符号后,从方程的一边移到另一边,这种变形叫做移项。
3.移项要改变符号.
2.解一元一次方程需要移项时我们把含未知数的项移到方程的一边(通常移到左边),常数项移到方程的另一边(通常移到右边).
这节课我们学习了什么?
移项
