陕西省榆林市第十二中学2021届高三上学期第三次月考(12月)数学(理)试题 Word版含答案解析
文档属性
| 名称 | 陕西省榆林市第十二中学2021届高三上学期第三次月考(12月)数学(理)试题 Word版含答案解析 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 00:00:00 | ||
图片预览




文档简介
榆林市第十二中学2020-2021学年第一学期高三年级
第三次质量检测理数试题
试卷满分:150分(Ⅰ卷60分,Ⅱ卷90分)
第I卷(选择题)
一、单选题(每小题5分,共60分)
1.已知集合false,false,则false( )
A.false B.false C.false D.false
2.投掷两颗骰子,其向上的点数分别为m和n,则复数false为纯虚数的概率为( )
A.false B.false C.false D.false
3.false展开式false的系数为( )
A.-10 B.10 C.-30 D.30
4.设数列false的前n项和为false,且falsefalse,则false( )
A.-7 B.-3 C.3 D.7
5.函数false(false且false)与false在同一坐标系内的图象可能是( )
A. B. C. D.
6.向量false,false满足false,false,且false,则false在false方向上的投影为( )
A.false B.-1 C.false D.1
7.抛物线false的准线被圆false截得的线段长为( )
A.4 B.false C.false D.2
8.函数false(false,false)的图象如图所示,为了得到false的图象,则只将false的图象( )
A.左移false个单位 B.右移false个单位
C.左移false个单位 D.右移false个单位
9.一对夫妇带着他们的两个小孩一起去观看影片,订购的4张电影票恰好在同一排且连在一起.影院要求每个小孩子要有家长相邻陪坐,则不同的坐法种数是( )
A.8 B.12 C.16 D.20
10.已知定义在R上的偶函数false在false上单调递增,则( )
A.false B.false
C.false D.false
11.已知点false,false分别是双曲线false(false,false)的左、右焦点,过点false且垂直于x轴的直线与双曲线交于A,B两点,若false是锐角三角形,则该双曲线离心率的取值范围是( )
A.false B.false C.false D.false
12.设函数false在false上的导函数为false,false在false上的导函数为false,若在false上false恒成立,则称函数false在false上为“凸函数”.已知false在false上为“凸函数”,则实数p的取值范围是( )
A.false B.false C.false D.false
第II卷(非选择题)
二、填空题(共20分)
13.若幂函数false的图象过点false,则曲线false在点false处的切线方程为______.
14.已知角false终边上一点false,则false________.
15.口袋中有形状,大小都相同的6只球,其中一只白球,2只红球,3只黄球,从袋中随机摸出2只球,则这2只球颜色不同的概率为_______.
16.将正三棱锥false置于水平反射镜面上,得“倒影三棱锥”false如图,下列关于该“倒影三棱锥”的说法中,正确的有_________.
①false平面false;
②若P,A,B,C在同一球面上,则Q也在该球面上;
③若该“倒影三棱锥”存在外接球,则false;
④若false,则false的中点必为“倒影三棱锥”外接球的球心
三、解答题(第一题10分,其余各题12分,共70分)
17.false的内角A、B、C的对边分别为a、b、c,已知false.
(1)求A; (2)若false,false的面积为false,求a.
18.数列false的前n项和为false,false,点false在直线false(false).
(1)求证:数列false是等差数列,并求false的通项公式;
(2)若数列false满足false,求数列false的前n项和false.
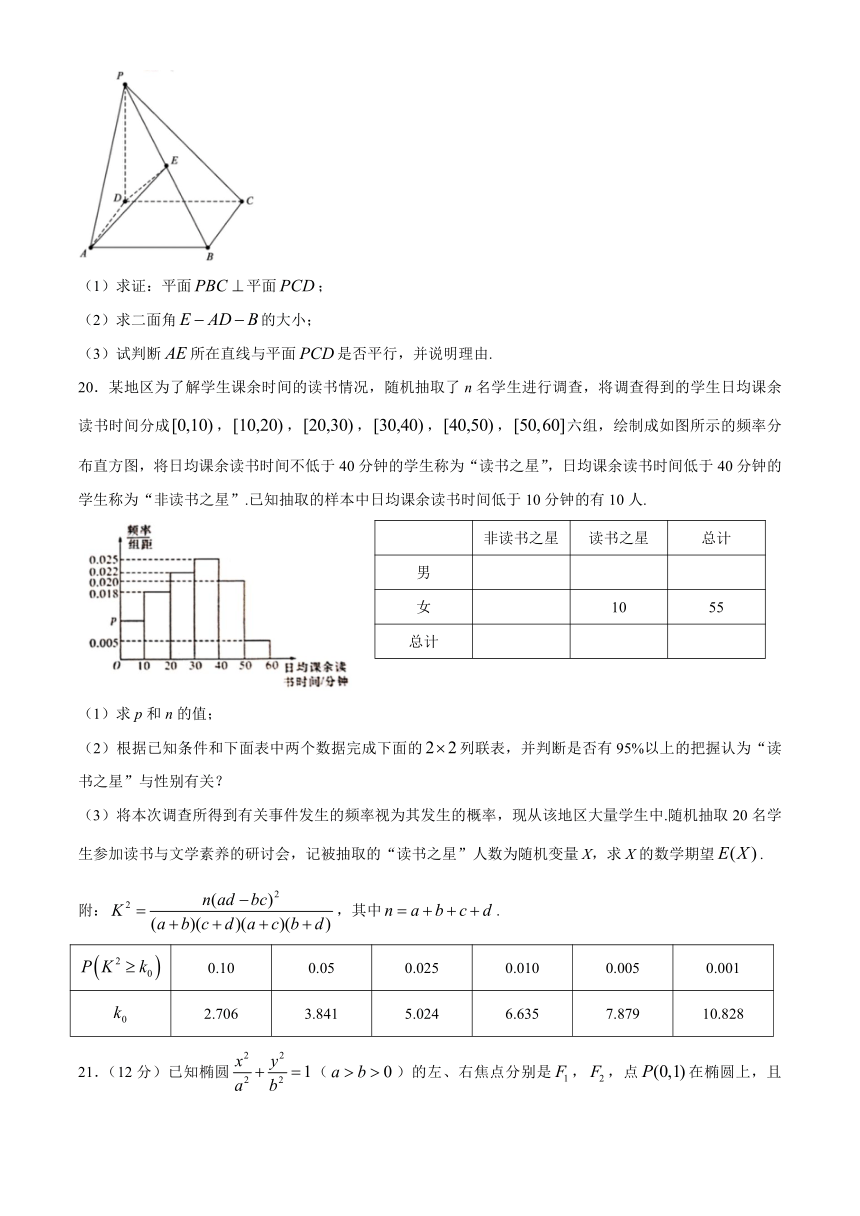
19.在四棱锥false中,底面false是正方形,false平面false,false,E是false的中点.
(1)求证:平面false平面false;
(2)求二面角false的大小;
(3)试判断false所在直线与平面false是否平行,并说明理由.
20.某地区为了解学生课余时间的读书情况,随机抽取了n名学生进行调查,将调查得到的学生日均课余读书时间分成false,false,false,false,false,false六组,绘制成如图所示的频率分布直方图,将日均课余读书时间不低于40分钟的学生称为“读书之星”,日均课余读书时间低于40分钟的学生称为“非读书之星”.已知抽取的样本中日均课余读书时间低于10分钟的有10人.
非读书之星
读书之星
总计
男
女
10
55
总计
(1)求p和n的值;
(2)根据已知条件和下面表中两个数据完成下面的false列联表,并判断是否有95%以上的把握认为“读书之星”与性别有关?
(3)将本次调查所得到有关事件发生的频率视为其发生的概率,现从该地区大量学生中.随机抽取20名学生参加读书与文学素养的研讨会,记被抽取的“读书之星”人数为随机变量X,求X的数学期望false.
附:false,其中false.
false
0.10
0.05
0.025
0.010
0.005
0.001
false
2.706
3.841
5.024
6.635
7.879
10.828
21.(12分)已知椭圆false(false)的左、右焦点分别是false,false,点false在椭圆上,且false.
(1)求椭圆的标准方程;
(2)过点false且不过点P的直线l交椭圆于A,B两点,求证:直线false与false的斜率之和为定值.
22.(12分)已知函数false,false.
(1)当false时,若false在false上的最大值为10,求实数b的值;
(2)若对任意false,都有false恒成立,求实数a的取值范围.
高三理数参考答案
1.A
解:由false,得false,所以false,
由false,得false,解得false,所以false,
所以false.
2.C
由题意知m,false,
以false表示事件空间中的基本事件,
其中m是抛掷第一颗骰子时向上的点数,n是抛掷第二颗骰子时向上的点数,
则事件空间的基本事件总数为false个,
而false为纯虚数
则false,由于false,false,则false,
符合条件的基本事件有false,false,false,false,false,false共六个,
由古典概型的概率计算公式得false.
即复数false为纯虚数的概率为false.
3.A
false的通项公式为false,
因为false。
所以含false的项为:falsefalse,
false展开式false的系数为-10.
4.A
解:当false时,false,得false,
当false时,由false得false,两式相减得
false,即false,所以false,
所以数列false是以false为首项,2为公比的等比数列,
所以false,所以false,所以false.
5.C
解:当false时,false为增函数,false开口向上,对称轴false,
排除B,D;当false时,false为减函数,false开口向下,对称轴false,排除A,故选:C.
6.B
因为false,false,false,
所以false在false方向上的投影为false.
7.B
因为抛物线false的准线方程为false,
圆false整理得false,则圆心坐标为false,半径为false,
则圆心到直线false的距离为false,
因此false被圆false截得的弦长为false.
8.A
由图像观察可知,false,
所以false,则false,所以false,
根据图像过点false,所以false,则false,所以false,
函数false,
因此把false图像向左平移false个单位即得到false的函数图像.
9.C
四个元素全排列,再除去两个家长相邻和两个小孩相邻情况,故false.
10.D
∵偶函数false在false上单调递增,
∴函数false在false上单调递减,
∵false,false,
又false,false,∴false,false
∴false,∴false,
11.D
由题意知,若如下图示,则false,false,
∴false,false,
令false,则有false,
false是锐角三角形,有false,得false
∴false,而false可知:false的范围false
12.C
∵false,∴false,∴false,
∵false在false上为“凸函数”,
∴false在false上恒成立,即false在false上恒成立,
令false,false,∴false,
∴false在false上单调递增,∴false,
∴false,即false.
13.false
设false,将false代入,false,解得false,
∴false,则false,∴false,
则切线方程为false,即false.
14.false
由已知可得false,false,则false.
15.false
由题得“摸出两只球颜色相同”的概率为false.故“摸出两只球颜色不同”的概率为false.
16.①④
由“倒影三棱锥”的几何特征可知false平面false,①正确;
当P,A,B,C在同一球面上时,若false的外接圆不是球的最大圆,
则点false不在该球面上,②错误;
若该“倒影三棱锥”存在外接球,
则三棱锥false的外接球的半径与等边三角形false外接圆的半径相等,设其为false,
则false,false,
则false,③错误;
由③的推导可知该“倒影三棱锥”外接球的球心为false的中心,
即false的中点,④正确.
故正确的说法有①④.
17.(1)false(2)false
(1)∵false.
由正弦定理得false,即false,
∴false,∵false,∴false.
(2)∵false,∴false,
因为false,所以false
∴false,即false.
18.(1)证明见解析,false;(2)false.
(Ⅰ)false,则有:false数列false是以3为首项,1为公差的等差数列故false,∴false.
∴当false时,false,当false时,false,当false时也成立.
∴false
(Ⅱ)∵false,∴false,
∵false
∴false
∴false
∴false
false
解得:false
19.(1)证明见解析 (2)false (3)false与平面false不平行,详见解析
(1)证明:∵false是正方形,∴false
∵false平面false,false平面false,∴false
∵falsefalse,false平面false∴false平面false
又∵false平面false∴平面false平面false
(2)∵false平面false,false,false平面false
∴false,false
又∵false是正方形∴false∴false,false,false两两垂直
∴以false为原点如图建系,设false
∴false,false,false,false,false,false
∴false,false
又∵false平面false
∴平面false的法向量false
设平面false的法向量false
则false,false
∴false
令false,得false,false,∴false
∴false
∴二面角false的大小为false
(3)∵false,false,false
又false,false平面false,∴false平面false
∴平面false的法向量为false
又∵false
∴false与false不垂直,∴false与平面false不平行
20.(1)false,false;(2)填表见解析;没有;(3)false人.
(1)false,解得:false,
所以false.
(2)因为false,所以“读书之星”有false,
从而false列联表如下图所示:
非读书之星
读书之星
总计
男
30
15
45
女
45
10
55
总计
75
25
100
将false列联表中的数据代入公式计算得false,
因为false,所以没有95%以上的把握认为“读书之星”与性别有关.
(3)将频率视为概率,即从该地区学生中抽取一名学生是“读书之星”的概率为false.
由题意可知false,所以false(人).
21.(1)false;(2)证明见解析.
解:(1)根据点false在椭圆false上,得false.
由false,得false.
因为false,所以false,
所以椭圆的标准方程为false.
(2)若直线false的斜率不存在,则直线false的方程为false,与椭圆只有一个交点,不符合题意.
若直线false的斜率存在,设点false,false,直线l:false(false,false),
根据点false在直线false上,得false.
把false代入false,得false,
则false,false.
由false,false知,false,则false,false均不为0,
则直线false的斜率false,直线false的斜率false,false
falsefalse,
因为false,所以false,
即直线false与false的斜率之和为定值.
22.(1)-8;(2)false.
(1)当false时,由false,得false,
令false,得false或false.
当false变化时,false,false在false的变化情况如下表:
false
false
false
false
false
1
false
2
false
false
0
false
0
false
false
false
单调递减
极小值false
单调递增
极大值false
单调递减
false
所以false在false上的最大值为false,得false.
(2)由false,得false,
因为false,false且等号不能同时取得,
所以false,即false,
所以false恒成立,即false.
令false,false,则false,
当false时,false,false,从而false,
所以false在false上为增函数,所以false,
所以false.
第三次质量检测理数试题
试卷满分:150分(Ⅰ卷60分,Ⅱ卷90分)
第I卷(选择题)
一、单选题(每小题5分,共60分)
1.已知集合false,false,则false( )
A.false B.false C.false D.false
2.投掷两颗骰子,其向上的点数分别为m和n,则复数false为纯虚数的概率为( )
A.false B.false C.false D.false
3.false展开式false的系数为( )
A.-10 B.10 C.-30 D.30
4.设数列false的前n项和为false,且falsefalse,则false( )
A.-7 B.-3 C.3 D.7
5.函数false(false且false)与false在同一坐标系内的图象可能是( )
A. B. C. D.
6.向量false,false满足false,false,且false,则false在false方向上的投影为( )
A.false B.-1 C.false D.1
7.抛物线false的准线被圆false截得的线段长为( )
A.4 B.false C.false D.2
8.函数false(false,false)的图象如图所示,为了得到false的图象,则只将false的图象( )
A.左移false个单位 B.右移false个单位
C.左移false个单位 D.右移false个单位
9.一对夫妇带着他们的两个小孩一起去观看影片,订购的4张电影票恰好在同一排且连在一起.影院要求每个小孩子要有家长相邻陪坐,则不同的坐法种数是( )
A.8 B.12 C.16 D.20
10.已知定义在R上的偶函数false在false上单调递增,则( )
A.false B.false
C.false D.false
11.已知点false,false分别是双曲线false(false,false)的左、右焦点,过点false且垂直于x轴的直线与双曲线交于A,B两点,若false是锐角三角形,则该双曲线离心率的取值范围是( )
A.false B.false C.false D.false
12.设函数false在false上的导函数为false,false在false上的导函数为false,若在false上false恒成立,则称函数false在false上为“凸函数”.已知false在false上为“凸函数”,则实数p的取值范围是( )
A.false B.false C.false D.false
第II卷(非选择题)
二、填空题(共20分)
13.若幂函数false的图象过点false,则曲线false在点false处的切线方程为______.
14.已知角false终边上一点false,则false________.
15.口袋中有形状,大小都相同的6只球,其中一只白球,2只红球,3只黄球,从袋中随机摸出2只球,则这2只球颜色不同的概率为_______.
16.将正三棱锥false置于水平反射镜面上,得“倒影三棱锥”false如图,下列关于该“倒影三棱锥”的说法中,正确的有_________.
①false平面false;
②若P,A,B,C在同一球面上,则Q也在该球面上;
③若该“倒影三棱锥”存在外接球,则false;
④若false,则false的中点必为“倒影三棱锥”外接球的球心
三、解答题(第一题10分,其余各题12分,共70分)
17.false的内角A、B、C的对边分别为a、b、c,已知false.
(1)求A; (2)若false,false的面积为false,求a.
18.数列false的前n项和为false,false,点false在直线false(false).
(1)求证:数列false是等差数列,并求false的通项公式;
(2)若数列false满足false,求数列false的前n项和false.
19.在四棱锥false中,底面false是正方形,false平面false,false,E是false的中点.
(1)求证:平面false平面false;
(2)求二面角false的大小;
(3)试判断false所在直线与平面false是否平行,并说明理由.
20.某地区为了解学生课余时间的读书情况,随机抽取了n名学生进行调查,将调查得到的学生日均课余读书时间分成false,false,false,false,false,false六组,绘制成如图所示的频率分布直方图,将日均课余读书时间不低于40分钟的学生称为“读书之星”,日均课余读书时间低于40分钟的学生称为“非读书之星”.已知抽取的样本中日均课余读书时间低于10分钟的有10人.
非读书之星
读书之星
总计
男
女
10
55
总计
(1)求p和n的值;
(2)根据已知条件和下面表中两个数据完成下面的false列联表,并判断是否有95%以上的把握认为“读书之星”与性别有关?
(3)将本次调查所得到有关事件发生的频率视为其发生的概率,现从该地区大量学生中.随机抽取20名学生参加读书与文学素养的研讨会,记被抽取的“读书之星”人数为随机变量X,求X的数学期望false.
附:false,其中false.
false
0.10
0.05
0.025
0.010
0.005
0.001
false
2.706
3.841
5.024
6.635
7.879
10.828
21.(12分)已知椭圆false(false)的左、右焦点分别是false,false,点false在椭圆上,且false.
(1)求椭圆的标准方程;
(2)过点false且不过点P的直线l交椭圆于A,B两点,求证:直线false与false的斜率之和为定值.
22.(12分)已知函数false,false.
(1)当false时,若false在false上的最大值为10,求实数b的值;
(2)若对任意false,都有false恒成立,求实数a的取值范围.
高三理数参考答案
1.A
解:由false,得false,所以false,
由false,得false,解得false,所以false,
所以false.
2.C
由题意知m,false,
以false表示事件空间中的基本事件,
其中m是抛掷第一颗骰子时向上的点数,n是抛掷第二颗骰子时向上的点数,
则事件空间的基本事件总数为false个,
而false为纯虚数
则false,由于false,false,则false,
符合条件的基本事件有false,false,false,false,false,false共六个,
由古典概型的概率计算公式得false.
即复数false为纯虚数的概率为false.
3.A
false的通项公式为false,
因为false。
所以含false的项为:falsefalse,
false展开式false的系数为-10.
4.A
解:当false时,false,得false,
当false时,由false得false,两式相减得
false,即false,所以false,
所以数列false是以false为首项,2为公比的等比数列,
所以false,所以false,所以false.
5.C
解:当false时,false为增函数,false开口向上,对称轴false,
排除B,D;当false时,false为减函数,false开口向下,对称轴false,排除A,故选:C.
6.B
因为false,false,false,
所以false在false方向上的投影为false.
7.B
因为抛物线false的准线方程为false,
圆false整理得false,则圆心坐标为false,半径为false,
则圆心到直线false的距离为false,
因此false被圆false截得的弦长为false.
8.A
由图像观察可知,false,
所以false,则false,所以false,
根据图像过点false,所以false,则false,所以false,
函数false,
因此把false图像向左平移false个单位即得到false的函数图像.
9.C
四个元素全排列,再除去两个家长相邻和两个小孩相邻情况,故false.
10.D
∵偶函数false在false上单调递增,
∴函数false在false上单调递减,
∵false,false,
又false,false,∴false,false
∴false,∴false,
11.D
由题意知,若如下图示,则false,false,
∴false,false,
令false,则有false,
false是锐角三角形,有false,得false
∴false,而false可知:false的范围false
12.C
∵false,∴false,∴false,
∵false在false上为“凸函数”,
∴false在false上恒成立,即false在false上恒成立,
令false,false,∴false,
∴false在false上单调递增,∴false,
∴false,即false.
13.false
设false,将false代入,false,解得false,
∴false,则false,∴false,
则切线方程为false,即false.
14.false
由已知可得false,false,则false.
15.false
由题得“摸出两只球颜色相同”的概率为false.故“摸出两只球颜色不同”的概率为false.
16.①④
由“倒影三棱锥”的几何特征可知false平面false,①正确;
当P,A,B,C在同一球面上时,若false的外接圆不是球的最大圆,
则点false不在该球面上,②错误;
若该“倒影三棱锥”存在外接球,
则三棱锥false的外接球的半径与等边三角形false外接圆的半径相等,设其为false,
则false,false,
则false,③错误;
由③的推导可知该“倒影三棱锥”外接球的球心为false的中心,
即false的中点,④正确.
故正确的说法有①④.
17.(1)false(2)false
(1)∵false.
由正弦定理得false,即false,
∴false,∵false,∴false.
(2)∵false,∴false,
因为false,所以false
∴false,即false.
18.(1)证明见解析,false;(2)false.
(Ⅰ)false,则有:false数列false是以3为首项,1为公差的等差数列故false,∴false.
∴当false时,false,当false时,false,当false时也成立.
∴false
(Ⅱ)∵false,∴false,
∵false
∴false
∴false
∴false
false
解得:false
19.(1)证明见解析 (2)false (3)false与平面false不平行,详见解析
(1)证明:∵false是正方形,∴false
∵false平面false,false平面false,∴false
∵falsefalse,false平面false∴false平面false
又∵false平面false∴平面false平面false
(2)∵false平面false,false,false平面false
∴false,false
又∵false是正方形∴false∴false,false,false两两垂直
∴以false为原点如图建系,设false
∴false,false,false,false,false,false
∴false,false
又∵false平面false
∴平面false的法向量false
设平面false的法向量false
则false,false
∴false
令false,得false,false,∴false
∴false
∴二面角false的大小为false
(3)∵false,false,false
又false,false平面false,∴false平面false
∴平面false的法向量为false
又∵false
∴false与false不垂直,∴false与平面false不平行
20.(1)false,false;(2)填表见解析;没有;(3)false人.
(1)false,解得:false,
所以false.
(2)因为false,所以“读书之星”有false,
从而false列联表如下图所示:
非读书之星
读书之星
总计
男
30
15
45
女
45
10
55
总计
75
25
100
将false列联表中的数据代入公式计算得false,
因为false,所以没有95%以上的把握认为“读书之星”与性别有关.
(3)将频率视为概率,即从该地区学生中抽取一名学生是“读书之星”的概率为false.
由题意可知false,所以false(人).
21.(1)false;(2)证明见解析.
解:(1)根据点false在椭圆false上,得false.
由false,得false.
因为false,所以false,
所以椭圆的标准方程为false.
(2)若直线false的斜率不存在,则直线false的方程为false,与椭圆只有一个交点,不符合题意.
若直线false的斜率存在,设点false,false,直线l:false(false,false),
根据点false在直线false上,得false.
把false代入false,得false,
则false,false.
由false,false知,false,则false,false均不为0,
则直线false的斜率false,直线false的斜率false,false
falsefalse,
因为false,所以false,
即直线false与false的斜率之和为定值.
22.(1)-8;(2)false.
(1)当false时,由false,得false,
令false,得false或false.
当false变化时,false,false在false的变化情况如下表:
false
false
false
false
false
1
false
2
false
false
0
false
0
false
false
false
单调递减
极小值false
单调递增
极大值false
单调递减
false
所以false在false上的最大值为false,得false.
(2)由false,得false,
因为false,false且等号不能同时取得,
所以false,即false,
所以false恒成立,即false.
令false,false,则false,
当false时,false,false,从而false,
所以false在false上为增函数,所以false,
所以false.
同课章节目录
