沪教版(上海)初中数学九年级第一学期第26章: 二次函数复习课 课件(18张)
文档属性
| 名称 | 沪教版(上海)初中数学九年级第一学期第26章: 二次函数复习课 课件(18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 334.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-27 21:13:11 | ||
图片预览






文档简介
(共18张PPT)
二次函数复习课
二次函数一般考点:
1、二次函数的定义
2、二次函数的图象及性质
3、求二次函数的解析式
4、a,b,c符号的确定
5、抛物线的平移法则
6、二次函数与一元二次方程的关系
7、二次函数的综合运用
1、二次函数的定义
定义:y=ax?+bx+c
(
a
、b
、
c
是常数,
a
≠
0
)
条件:①a
≠
0
②最高次数为2
③代数式一定是整式
1、y=-x?,
,
y=100-5x?,y=3x?-2x?+5,
其中是二次函数的有____个。
2
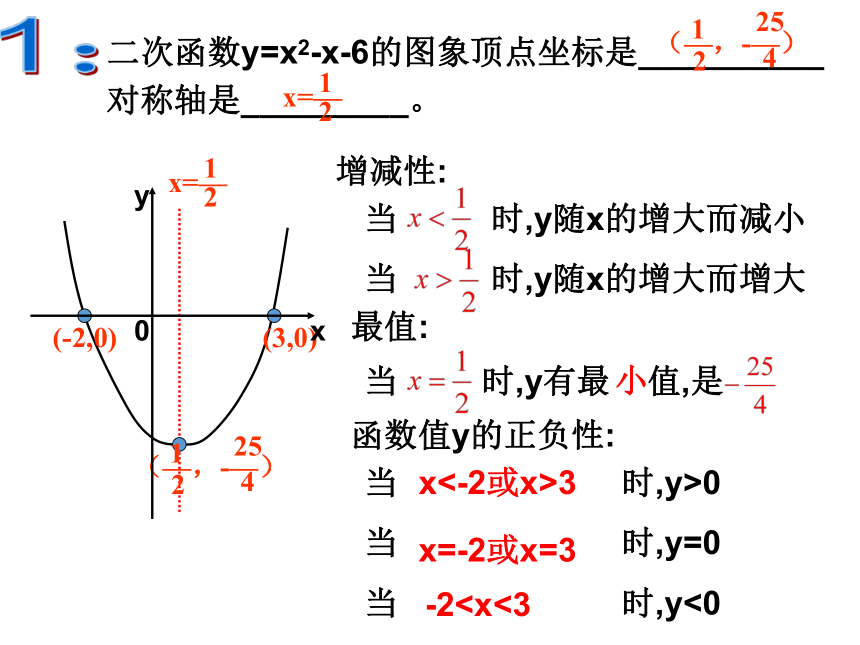
二次函数y=x2-x-6的图象顶点坐标是__________
对称轴是_________。
例1:
(—,— )
1
25
2
4
x=—
1
2
一般式 y=ax?+bx+c
顶点式 y=a(x-h)?+k
二次函数的解析式:
(a≠0)
对称轴:直线x=h
顶点:(h,k)
二次函数的图象:
是一条抛物线
二次函数的图象的性质:
开口方向;
对称轴;
顶点坐标;
增减性;
最值
2、二次函数的图象及性质
二次函数y=x2-x-6的图象顶点坐标是__________
对称轴是_________。
1:
(—,-—)
1
25
2
4
x=—
1
2
x=—
1
2
(—,-—)
1
25
2
4
(-2,0)
(3,0)
0
x
y
增减性:
当
时,y随x的增大而减小
当
时,y随x的增大而增大
最值:
当
时,y有最
值,是
小
函数值y的正负性:
当
时,y>0
当
时,y=0
当
时,y<0
x<-2或x>3
x=-2或x=3
-21、根据下列条件,求二次函数的解析式。
(1)、图象经过(0,0),
(1,-2)
,
(2,3)
三点;
(2)、图象的顶点(2,3),
且经过点(3,1)
;
(3)、图象经过(0,0),
(12,0)
,且最高点
的纵坐标是3
。
4、a,b,c符号的确定
a
a,b
c
△
a决定开口方向和大小:a>0时开口向上,
a<0时开口向下
a、b同时决定对称轴位置:a、b同号时对称轴在y轴左侧
a、b异号时对称轴在y轴右侧
b=0时对称轴是y轴
c决定抛物线与y轴的交点:c>0时抛物线交于y轴的正半轴
c=0时抛物线过原点
c<0时抛物线交于y轴的负半轴
△决定抛物线与x轴的交点:△>0时抛物线与x轴有两个交点
△=0时抛物线与x轴有一个交点
△<0时抛物线与x轴没有交点
(上正、下负)
(左同、右异)
(上正、下负)
△=
b2-4ac
-2
二次函数y=ax2+bx+c(a≠0)的几个特例:
1)、当x=1
时,
2)、当x=-1时,
3)、当x=2时,
4)、当x=-2时,
y=
y=
y=
y=
6)、2a+b
0.
x
y
o
1
-1
2
>0
=0
>0
<0
>
5)、b?-4ac
0.
<
a+b+c
a-b+c
4a+2b+c
4a-2b+c
例2:如图所示,二次函数y=ax2+bx+c的图像开口向上,图像经过点(-1,2)和(1,0)且与y轴交于负半轴.
问:给出五个结论:①a>0;②b>0;③c>0;④a+b+c=0;
⑤a-b+c<1.其中正确的结论的序号是
(
)
①④
x
y
1、二次函数y=ax2+bx+c(a≠0)的图象如图
所示,则a、b、c的符号为( )
A、a<0,b>0,c>0
B、a<0,b>0,c<0
C、a<0,b<0,c>0
D、a<0,b<0,c<0
x
y
2、二次函数y=ax2+bx+c(a≠0)的图象
如图所示,则a、b、c的符号为( )
A、a>0,b>0,c=0
B、a<0,b>0,c=0
C、a<0,b<0,c<0
D、a>0,b<0,c=0
x
y
3、二次函数y=ax2+bx+c(a≠0)的图象如图
所示,则a、b、c
、
△的符号为(
)
A、a>0,b=0,c>0,△>0
B、a<0,b>0,c<0,△=0
C、a>0,b=0,c<0,△>0
D、a<0,b=0,c<0,△<0
B
A
C
o
o
o
练习:
熟练掌握a,b,
c,△与抛物线图象的关系
(上正、下负)
(左同、右异)
·
c
已知二次函数y=ax2+bx+c
(a≠0)的图象如图,则下列结论中正确的是(
)
A.a>0
B.当x>1时,y随x的增大而增大
C.c<0
D.3是方程ax2+bx+c=0的一个根
D
5、抛物线的平移法则
左加右减,上加下减
练习
⑴二次函数y=2x2的图象向
平移
个单位可得到y=2x2-3的图象;
二次函数y=2x2的图象向
平移
个单位可得到y=2(x-3)2的图象。
⑵二次函数y=2x2的图象先向
平移
个单位,再向
平移
个单位可得到函数y=2(x+1)2+2的图象。
下
3
右
3
左
1
上
2
引申:y=2(x+3)2-4
y=2(x+1)2+2
判别式:
b2-4ac
二次函数
y=ax2+bx+c
(a≠0)
图象
一元二次方程ax2+bx+c=0
(a≠0)的根
x
y
O
与x轴有两个不
同的交点
(x1,0)
(x2,0)
有两个不同的解x=x1,x=x2
b2-4ac>0
x
y
O
与x轴有唯一个
交点
有两个相等的解
x1=x2=
b2-4ac=0
x
y
O
与x轴没有
交点
没有实数根
b2-4ac<0
6、二次函数与一元二次方程的关系
二次函数y=ax2+bx+c的图象和x轴交点有三种情况:
(1)有两个交点
(2)有一个交点
(3)没有交点
△=b2
–
4ac
>
0
△=
b2
–
4ac=
0
△=
b2
–
4ac<
0
若抛物线y=ax2+bx+c与x轴有交点,则
△=
b2
–
4ac
≥0
例2:已知抛物线y=x2-2x-8,
(1)求证:该抛物线与x轴一定有两个交点;
(2)若该抛物线与x轴的两个交点分别为A、B,且它的顶点为P,求△ABP的面积。
(1)证明:∵△=22-4
×
(-8)=36>0
∴该抛物线与x轴一定有两个交点
(2)解:∵抛物线与x轴相交时
x2-2x-8=0
解方程得:x1=4,
x2=-2
∴AB=|4-(-2)|=6
而P点坐标是(1,-9),PC=|-9|=9
S=1/2
AB×PC=
x
y
A
B
P
c
1.已知抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同,顶点在直线x=1上,且顶点到x轴的距离为5,请写出满足此条件的抛物线的解析式.
解:抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同
?
a=1或-1
又
顶点在直线x=1上,且顶点到x轴的距离为5,
?
顶点为(1,5)或(1,-5)
所以其解析式为:
(1)
y=(x-1)2+5
(2)
y=(x-1)2-5
(3)
y=-(x-1)2+5
(4)
y=-(x-1)2-5
展开成一般式即可.
7、二次函数的综合运用
2.若a+b+c=0,a?0,把抛物线y=ax2+bx+c向下平移
4个单位,再向左平移5个单位所到的新抛物线的
顶点是(-2,0),求原抛物线的解析式.
分析:
(1)由a+b+c=0可知,原抛物线的图象经过(1,0)
(2)
新抛物线向右平移5个单位,
再向上平移4个单位即得原抛物线
答案:y=-x2+6x-5
二次函数复习课
二次函数一般考点:
1、二次函数的定义
2、二次函数的图象及性质
3、求二次函数的解析式
4、a,b,c符号的确定
5、抛物线的平移法则
6、二次函数与一元二次方程的关系
7、二次函数的综合运用
1、二次函数的定义
定义:y=ax?+bx+c
(
a
、b
、
c
是常数,
a
≠
0
)
条件:①a
≠
0
②最高次数为2
③代数式一定是整式
1、y=-x?,
,
y=100-5x?,y=3x?-2x?+5,
其中是二次函数的有____个。
2
二次函数y=x2-x-6的图象顶点坐标是__________
对称轴是_________。
例1:
(—,— )
1
25
2
4
x=—
1
2
一般式 y=ax?+bx+c
顶点式 y=a(x-h)?+k
二次函数的解析式:
(a≠0)
对称轴:直线x=h
顶点:(h,k)
二次函数的图象:
是一条抛物线
二次函数的图象的性质:
开口方向;
对称轴;
顶点坐标;
增减性;
最值
2、二次函数的图象及性质
二次函数y=x2-x-6的图象顶点坐标是__________
对称轴是_________。
1:
(—,-—)
1
25
2
4
x=—
1
2
x=—
1
2
(—,-—)
1
25
2
4
(-2,0)
(3,0)
0
x
y
增减性:
当
时,y随x的增大而减小
当
时,y随x的增大而增大
最值:
当
时,y有最
值,是
小
函数值y的正负性:
当
时,y>0
当
时,y=0
当
时,y<0
x<-2或x>3
x=-2或x=3
-2
(1)、图象经过(0,0),
(1,-2)
,
(2,3)
三点;
(2)、图象的顶点(2,3),
且经过点(3,1)
;
(3)、图象经过(0,0),
(12,0)
,且最高点
的纵坐标是3
。
4、a,b,c符号的确定
a
a,b
c
△
a决定开口方向和大小:a>0时开口向上,
a<0时开口向下
a、b同时决定对称轴位置:a、b同号时对称轴在y轴左侧
a、b异号时对称轴在y轴右侧
b=0时对称轴是y轴
c决定抛物线与y轴的交点:c>0时抛物线交于y轴的正半轴
c=0时抛物线过原点
c<0时抛物线交于y轴的负半轴
△决定抛物线与x轴的交点:△>0时抛物线与x轴有两个交点
△=0时抛物线与x轴有一个交点
△<0时抛物线与x轴没有交点
(上正、下负)
(左同、右异)
(上正、下负)
△=
b2-4ac
-2
二次函数y=ax2+bx+c(a≠0)的几个特例:
1)、当x=1
时,
2)、当x=-1时,
3)、当x=2时,
4)、当x=-2时,
y=
y=
y=
y=
6)、2a+b
0.
x
y
o
1
-1
2
>0
=0
>0
<0
>
5)、b?-4ac
0.
<
a+b+c
a-b+c
4a+2b+c
4a-2b+c
例2:如图所示,二次函数y=ax2+bx+c的图像开口向上,图像经过点(-1,2)和(1,0)且与y轴交于负半轴.
问:给出五个结论:①a>0;②b>0;③c>0;④a+b+c=0;
⑤a-b+c<1.其中正确的结论的序号是
(
)
①④
x
y
1、二次函数y=ax2+bx+c(a≠0)的图象如图
所示,则a、b、c的符号为( )
A、a<0,b>0,c>0
B、a<0,b>0,c<0
C、a<0,b<0,c>0
D、a<0,b<0,c<0
x
y
2、二次函数y=ax2+bx+c(a≠0)的图象
如图所示,则a、b、c的符号为( )
A、a>0,b>0,c=0
B、a<0,b>0,c=0
C、a<0,b<0,c<0
D、a>0,b<0,c=0
x
y
3、二次函数y=ax2+bx+c(a≠0)的图象如图
所示,则a、b、c
、
△的符号为(
)
A、a>0,b=0,c>0,△>0
B、a<0,b>0,c<0,△=0
C、a>0,b=0,c<0,△>0
D、a<0,b=0,c<0,△<0
B
A
C
o
o
o
练习:
熟练掌握a,b,
c,△与抛物线图象的关系
(上正、下负)
(左同、右异)
·
c
已知二次函数y=ax2+bx+c
(a≠0)的图象如图,则下列结论中正确的是(
)
A.a>0
B.当x>1时,y随x的增大而增大
C.c<0
D.3是方程ax2+bx+c=0的一个根
D
5、抛物线的平移法则
左加右减,上加下减
练习
⑴二次函数y=2x2的图象向
平移
个单位可得到y=2x2-3的图象;
二次函数y=2x2的图象向
平移
个单位可得到y=2(x-3)2的图象。
⑵二次函数y=2x2的图象先向
平移
个单位,再向
平移
个单位可得到函数y=2(x+1)2+2的图象。
下
3
右
3
左
1
上
2
引申:y=2(x+3)2-4
y=2(x+1)2+2
判别式:
b2-4ac
二次函数
y=ax2+bx+c
(a≠0)
图象
一元二次方程ax2+bx+c=0
(a≠0)的根
x
y
O
与x轴有两个不
同的交点
(x1,0)
(x2,0)
有两个不同的解x=x1,x=x2
b2-4ac>0
x
y
O
与x轴有唯一个
交点
有两个相等的解
x1=x2=
b2-4ac=0
x
y
O
与x轴没有
交点
没有实数根
b2-4ac<0
6、二次函数与一元二次方程的关系
二次函数y=ax2+bx+c的图象和x轴交点有三种情况:
(1)有两个交点
(2)有一个交点
(3)没有交点
△=b2
–
4ac
>
0
△=
b2
–
4ac=
0
△=
b2
–
4ac<
0
若抛物线y=ax2+bx+c与x轴有交点,则
△=
b2
–
4ac
≥0
例2:已知抛物线y=x2-2x-8,
(1)求证:该抛物线与x轴一定有两个交点;
(2)若该抛物线与x轴的两个交点分别为A、B,且它的顶点为P,求△ABP的面积。
(1)证明:∵△=22-4
×
(-8)=36>0
∴该抛物线与x轴一定有两个交点
(2)解:∵抛物线与x轴相交时
x2-2x-8=0
解方程得:x1=4,
x2=-2
∴AB=|4-(-2)|=6
而P点坐标是(1,-9),PC=|-9|=9
S=1/2
AB×PC=
x
y
A
B
P
c
1.已知抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同,顶点在直线x=1上,且顶点到x轴的距离为5,请写出满足此条件的抛物线的解析式.
解:抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同
?
a=1或-1
又
顶点在直线x=1上,且顶点到x轴的距离为5,
?
顶点为(1,5)或(1,-5)
所以其解析式为:
(1)
y=(x-1)2+5
(2)
y=(x-1)2-5
(3)
y=-(x-1)2+5
(4)
y=-(x-1)2-5
展开成一般式即可.
7、二次函数的综合运用
2.若a+b+c=0,a?0,把抛物线y=ax2+bx+c向下平移
4个单位,再向左平移5个单位所到的新抛物线的
顶点是(-2,0),求原抛物线的解析式.
分析:
(1)由a+b+c=0可知,原抛物线的图象经过(1,0)
(2)
新抛物线向右平移5个单位,
再向上平移4个单位即得原抛物线
答案:y=-x2+6x-5
