北师大版九年级数学上册4.8图形的位似假期同步测试(Word版,含答案)
文档属性
| 名称 | 北师大版九年级数学上册4.8图形的位似假期同步测试(Word版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 396.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 14:58:56 | ||
图片预览




文档简介
1029970010375900北师大版九年级数学上册第四章4.8图形的位似 同步测试
一.选择题
1.已知点A的坐标是(2,1),以坐标原点O为位似中心,图像与原图形的位似比为2,则点false的坐标为( )
A.(1,false) B.(4,2) C.(1,false)或(-1,-false) D.(4,2)或(-4,-2)
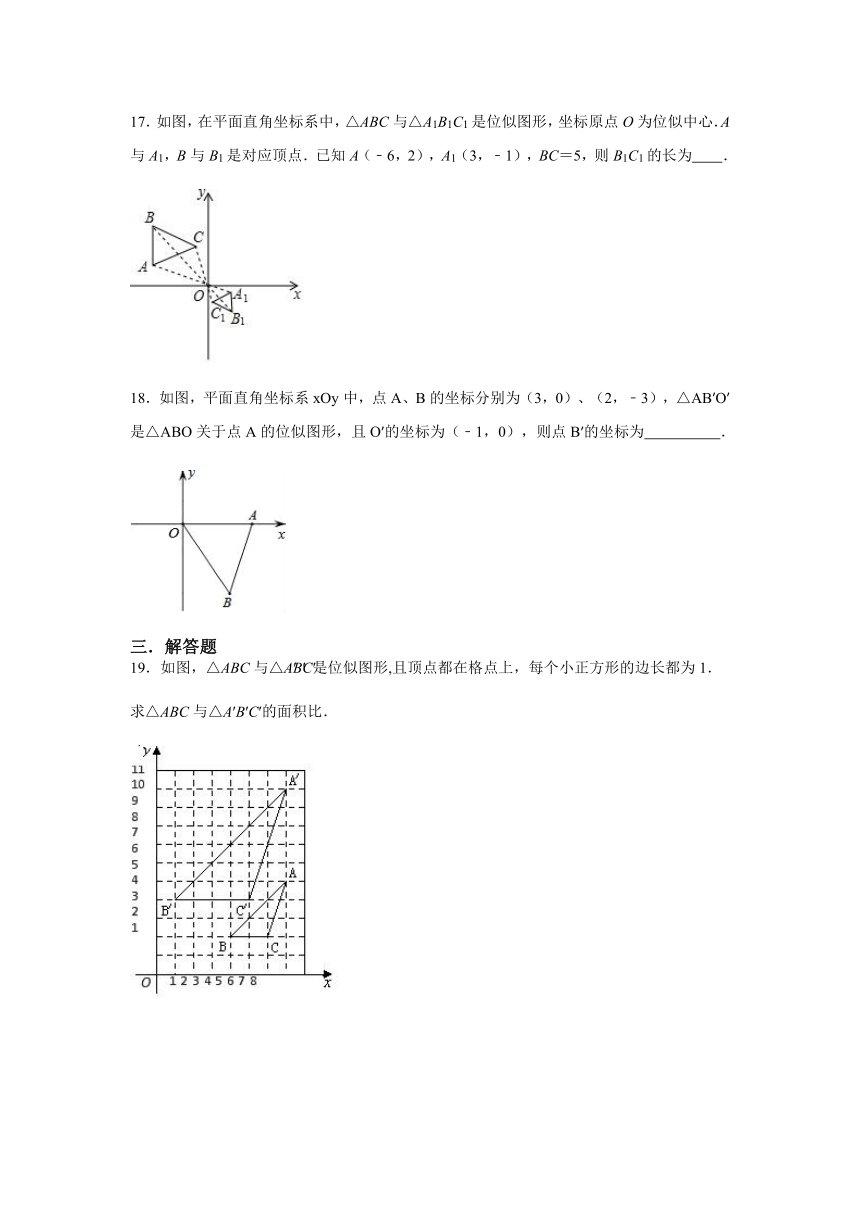
2.如图,△ABO缩小后变为△A′B′O,其中A、B的对应点分别为A′、B′点A、B、A′、B′均在图中在格点上.若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为( )
A.(,n) B.(m,n) C.(m,) D.()
3.(如图,线段AB两个端点的坐标分别为A(4,4),B(6,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,则端点C和D的坐标分别为( )
(2,2),(3,2) B.(2,4),(3,1)
C.(2,2),(3,1) D.(3,1),(2,2)
4.如图,线段CD两个端点的坐标分别为C(1,2)、D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B坐标为(5,0),则点A的坐标为( )
A.(2,5) B.(2.5,5) C.(3,5) D.(3,6)
5.如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD.若B(1,0),则点C的坐标为( )
A.(1,2) B.(1,1) C.(,) D.(2,1)
6.如图,△DEF与△ABC是位似图形,点O是位似中心,D、E、F分别是OA、OB、OC的中点,则△DEF与△ABC的面积比是( )
A.1:6 B.1:5 C.1:4 D.1:2
7.在平面直角坐标系中,已知点E(﹣4,2),F(﹣2,﹣2),以原点O为位似中心,相似比为,把△EFO缩小,则点E的对应点E′的坐标是( )
A.(﹣2,1) B.(﹣8,4)
C.(﹣8,4)或(8,﹣4) D.(﹣2,1)或(2,﹣1)
8.已知,直角坐标系中,点E(-4,2),F(-1,-1),以O为位似中心,按比例尺2:1把△EFO缩小,则点E的对应点false的坐标为( )
(2,-1)或(-2,1) B.(8,-4)或(-8,4)
C.(2,-1) D.(8,-4)
9.如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABO与△A′B′O′是以点P为位似中心的位似图形,它们的顶点均在格点(网格线的交点)上,则点P的坐标为( )
A.(0,0) B.(0,1) C.(﹣3,2) D.(3,﹣2)
10.如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比为1:false,点A的坐标为(0,1),则点E的坐标是( )
A.(-1.4,-1.4) B.(1.4,1.4) C.(-false,-false) D.(false,false)
二.填空题
11.如图,△ABC与△DEF位似,位似中心为点O,且△ABC的面积等于△DEF面积的,则AB:DE= .
12.△ABC与△A′B′C′是位似图形,且△ABC与△false的位似比是1:2,已知△ABC的面积是3,则△false的面积是
13.在平面直角坐标系中,△ABC和△A1B1C1的相似比等于,并且是关于原点O的位似图形,若点A的坐标为(3,6),则其对应点A1的坐标是 .
14.如果两个三角形不仅是相似三角形,而且每组对应点的连线交于一点,那么这两个三角形叫做位似三角形,这个点叫做位似中心.如图,△ABC和△A1B1C1是以点O为位似中心的位似三角形,若C1为OC的中点,AB=4.则A1B1的长为 .
15.在平面直角坐标系中,△ABC的顶点坐标分别是A(6,8),B(7,0),C(7,8)以原点O为位似中心,相似比为,把△ABC缩小,得到△A1B1C1,则点A的对应点A1的坐标为 .
16.如图,在平面直角坐标系中,点A、B的坐标分别为(﹣4,4)、(0,4),点C、D的坐标分别为(0,1)、(2,1).若线段AB和CD是位似图形,且位似中心在y轴上,则位似中心的坐标为 .
17.如图,在平面直角坐标系中,△ABC与△A1B1C1是位似图形,坐标原点O为位似中心.A与A1,B与B1是对应顶点.已知A(﹣6,2),A1(3,﹣1),BC=5,则B1C1的长为 .
18.如图,平面直角坐标系xOy中,点A、B的坐标分别为(3,0)、(2,﹣3),△AB′O′是△ABO关于点A的位似图形,且O′的坐标为(﹣1,0),则点B′的坐标为 .
三.解答题
19.如图,△ABC与△A′B′C′是位似图形,且顶点都在格点上,每个小正方形的边长都为1.
求△ABC与△A′B′C′的面积比.
20.如图,在边上为1个单位长度的小正方形网格中:
(1)画出△ABC向上平移6个单位长度,再向右平移5个单位长度后的△A1B1C1.
(2)以点B为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,请在网格中画出△A2B2C2.
(3)求△CC1C2的面积.
21.如图,四边形ABCD和四边形false位似,位似比false=2,四边形A′B′C′D′和四边形false位似,位似比false=1.四边形false和四边形ABCD是位似图形吗?位似比是多少?
22.如图,将△ABC在网格中(网格中每个小正方形的边长均为1)依次进行位似变换、轴对称变换和平移变换后得到△A3B3C3.
(1)△ABC与△A1B1C1的位似比等于 ;
(2)在网格中画出△A1B1C1关于y轴的轴对称图形△A2B2C2;
(3)请写出△A3B3C3是由△A2B2C2怎样平移得到的?
(4)设点P(x,y)为△ABC内一点,依次经过上述三次变换后,点P的对应点的坐标为 .
23.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点坐标;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点坐标;
(3)如果点D(a,b)在线段AB上,请直接写出经过(2)的变化后点D的对应点D2的坐标.
24.如图,在平面直角坐标系中,△ABC和△A1B1C1关于点E成中心对称,
(1)在图中标出点E,且点E的坐标为 ;
(2)点P(a,b)是△ABC边AB上一点,△ABC经过平移后点P的对应点P′的坐标为(a﹣6,b+2),请画出上述平移后的△A2B2C2,此时A2的坐标为 ,C2的坐标为 ;
(3)若△A1B1C1和△A2B2C2关于点F成位似三角形,则点F的坐标为 .
25.如图,利用直尺、计算机或图形计算器任意画一个△ABC,以点O为位似中心,自选相似比k,进行位似变换,得到△A'B′C′.度量线段OA,OA′,OB,OB′,OC,OC′的长,你有什么发现?任意改变△ABC的位置,得出的结论是否仍然成立?
答案提示
1.D.2.D.3.C.4.B.5.B.6.C.7.D.8.A.9.C. 10.D.
11.2:3. 12.12. 13.(9,18)或(﹣9,﹣18). 14.2.
15.(3,4)或(﹣3,﹣4). 16.(0,2).17..
18.解:过点B作BE⊥x轴于点E,B′作B′F⊥x轴于点F,
∵点A、B的坐标分别为(3,0)、(2,﹣3),△AB′O′是△ABO关于的A的位似图形,且O′的坐标为(﹣1,0),
∴==,AE=1,EO=2,BE=3,
∴==,
∴=,
解得:AF=,
∴EF=,
∴FO=2﹣=,
∵=,
解得:B′F=4,
则点B′的坐标为:(,﹣4).
故答案为:(,﹣4).
19.解:∵由已知条件可知false∽false
∴false.
20.解:(1)如图所示:
;
(2)如图所示:
;
(3)如图所示:
△CC1C2的面积为×3×6=9.
21.解:∵四边形ABCD和四边形false位似,
∴四边形ABCD∽四边形false.
∵四边形false和四边形false位似,
∴四边形false∽四边形false.
∴四边形false∽四边形ABCD.
∵对应顶点的连线过同一点,
∴四边形false和四边形ABCD是位似图形.
∵四边形ABCD和四边形false位似,位似比false=2,
四边形false和四边形false位似,位似比false=1,
∴四边形false和四边形ABCD的位似比为false.
22.解:(1))△ABC与△A1B1C1的位似比等于=;
(2)如图所示
(3)△A3B3C3是由△A2B2C2沿x轴向左平移2个单位,再沿y轴向上平移2个单位得到;
(4)点P(x,y)为△ABC内一点,依次经过上述三次变换后,点P的对应点的坐标为(﹣2x﹣2,2y+2).
故答案为:;(﹣2x﹣2,2y+2).
23.解:(1)如图所示:△A1B1C1,即为所求,
C1点坐标为:(3,2);
(2)如图所示:△A2B2C2,即为所求,
C2点坐标为:(﹣6,4);
(3)如果点D(a,b)在线段AB上,经过(2)的变化后D的对应点D2的坐标为:(2a,2b).
24.解:(1)如图,线段BB1的中点即为点E,
∵B(1,1),B1(﹣1,﹣3)
∴E(0,﹣1);
(2)如图,
∵点P(a,b)是△ABC边AB上一点,△ABC经过平移后点P的对应点P′的坐标为(a﹣6,b+2),
又∵A(3,2),C(4,0),
∴A2(﹣3,4),C2(﹣2,2);
(3)∵对应顶点A1A2与B1B2的连线交于点(﹣3,0),
∴F(﹣3,0).
25.解:经测量,OA=2cm,OA′=1cm,OB=3cm,OB′=1.5cm,OC=3cm,OC′=1.5cm,
可以得到,===2,
∴A′B′∥AB,A′C′∥AC,C′B′∥CB,即位似图形的对应边互相平行,
任意改变△ABC的位置,得到△A'B′C′,△ABC与△A'B′C′的对应边互相平行,
即意改变△ABC的位置,得出的结论仍然成立.
一.选择题
1.已知点A的坐标是(2,1),以坐标原点O为位似中心,图像与原图形的位似比为2,则点false的坐标为( )
A.(1,false) B.(4,2) C.(1,false)或(-1,-false) D.(4,2)或(-4,-2)
2.如图,△ABO缩小后变为△A′B′O,其中A、B的对应点分别为A′、B′点A、B、A′、B′均在图中在格点上.若线段AB上有一点P(m,n),则点P在A′B′上的对应点P′的坐标为( )
A.(,n) B.(m,n) C.(m,) D.()
3.(如图,线段AB两个端点的坐标分别为A(4,4),B(6,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,则端点C和D的坐标分别为( )
(2,2),(3,2) B.(2,4),(3,1)
C.(2,2),(3,1) D.(3,1),(2,2)
4.如图,线段CD两个端点的坐标分别为C(1,2)、D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B坐标为(5,0),则点A的坐标为( )
A.(2,5) B.(2.5,5) C.(3,5) D.(3,6)
5.如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD.若B(1,0),则点C的坐标为( )
A.(1,2) B.(1,1) C.(,) D.(2,1)
6.如图,△DEF与△ABC是位似图形,点O是位似中心,D、E、F分别是OA、OB、OC的中点,则△DEF与△ABC的面积比是( )
A.1:6 B.1:5 C.1:4 D.1:2
7.在平面直角坐标系中,已知点E(﹣4,2),F(﹣2,﹣2),以原点O为位似中心,相似比为,把△EFO缩小,则点E的对应点E′的坐标是( )
A.(﹣2,1) B.(﹣8,4)
C.(﹣8,4)或(8,﹣4) D.(﹣2,1)或(2,﹣1)
8.已知,直角坐标系中,点E(-4,2),F(-1,-1),以O为位似中心,按比例尺2:1把△EFO缩小,则点E的对应点false的坐标为( )
(2,-1)或(-2,1) B.(8,-4)或(-8,4)
C.(2,-1) D.(8,-4)
9.如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系,△ABO与△A′B′O′是以点P为位似中心的位似图形,它们的顶点均在格点(网格线的交点)上,则点P的坐标为( )
A.(0,0) B.(0,1) C.(﹣3,2) D.(3,﹣2)
10.如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比为1:false,点A的坐标为(0,1),则点E的坐标是( )
A.(-1.4,-1.4) B.(1.4,1.4) C.(-false,-false) D.(false,false)
二.填空题
11.如图,△ABC与△DEF位似,位似中心为点O,且△ABC的面积等于△DEF面积的,则AB:DE= .
12.△ABC与△A′B′C′是位似图形,且△ABC与△false的位似比是1:2,已知△ABC的面积是3,则△false的面积是
13.在平面直角坐标系中,△ABC和△A1B1C1的相似比等于,并且是关于原点O的位似图形,若点A的坐标为(3,6),则其对应点A1的坐标是 .
14.如果两个三角形不仅是相似三角形,而且每组对应点的连线交于一点,那么这两个三角形叫做位似三角形,这个点叫做位似中心.如图,△ABC和△A1B1C1是以点O为位似中心的位似三角形,若C1为OC的中点,AB=4.则A1B1的长为 .
15.在平面直角坐标系中,△ABC的顶点坐标分别是A(6,8),B(7,0),C(7,8)以原点O为位似中心,相似比为,把△ABC缩小,得到△A1B1C1,则点A的对应点A1的坐标为 .
16.如图,在平面直角坐标系中,点A、B的坐标分别为(﹣4,4)、(0,4),点C、D的坐标分别为(0,1)、(2,1).若线段AB和CD是位似图形,且位似中心在y轴上,则位似中心的坐标为 .
17.如图,在平面直角坐标系中,△ABC与△A1B1C1是位似图形,坐标原点O为位似中心.A与A1,B与B1是对应顶点.已知A(﹣6,2),A1(3,﹣1),BC=5,则B1C1的长为 .
18.如图,平面直角坐标系xOy中,点A、B的坐标分别为(3,0)、(2,﹣3),△AB′O′是△ABO关于点A的位似图形,且O′的坐标为(﹣1,0),则点B′的坐标为 .
三.解答题
19.如图,△ABC与△A′B′C′是位似图形,且顶点都在格点上,每个小正方形的边长都为1.
求△ABC与△A′B′C′的面积比.
20.如图,在边上为1个单位长度的小正方形网格中:
(1)画出△ABC向上平移6个单位长度,再向右平移5个单位长度后的△A1B1C1.
(2)以点B为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,请在网格中画出△A2B2C2.
(3)求△CC1C2的面积.
21.如图,四边形ABCD和四边形false位似,位似比false=2,四边形A′B′C′D′和四边形false位似,位似比false=1.四边形false和四边形ABCD是位似图形吗?位似比是多少?
22.如图,将△ABC在网格中(网格中每个小正方形的边长均为1)依次进行位似变换、轴对称变换和平移变换后得到△A3B3C3.
(1)△ABC与△A1B1C1的位似比等于 ;
(2)在网格中画出△A1B1C1关于y轴的轴对称图形△A2B2C2;
(3)请写出△A3B3C3是由△A2B2C2怎样平移得到的?
(4)设点P(x,y)为△ABC内一点,依次经过上述三次变换后,点P的对应点的坐标为 .
23.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点坐标;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点坐标;
(3)如果点D(a,b)在线段AB上,请直接写出经过(2)的变化后点D的对应点D2的坐标.
24.如图,在平面直角坐标系中,△ABC和△A1B1C1关于点E成中心对称,
(1)在图中标出点E,且点E的坐标为 ;
(2)点P(a,b)是△ABC边AB上一点,△ABC经过平移后点P的对应点P′的坐标为(a﹣6,b+2),请画出上述平移后的△A2B2C2,此时A2的坐标为 ,C2的坐标为 ;
(3)若△A1B1C1和△A2B2C2关于点F成位似三角形,则点F的坐标为 .
25.如图,利用直尺、计算机或图形计算器任意画一个△ABC,以点O为位似中心,自选相似比k,进行位似变换,得到△A'B′C′.度量线段OA,OA′,OB,OB′,OC,OC′的长,你有什么发现?任意改变△ABC的位置,得出的结论是否仍然成立?
答案提示
1.D.2.D.3.C.4.B.5.B.6.C.7.D.8.A.9.C. 10.D.
11.2:3. 12.12. 13.(9,18)或(﹣9,﹣18). 14.2.
15.(3,4)或(﹣3,﹣4). 16.(0,2).17..
18.解:过点B作BE⊥x轴于点E,B′作B′F⊥x轴于点F,
∵点A、B的坐标分别为(3,0)、(2,﹣3),△AB′O′是△ABO关于的A的位似图形,且O′的坐标为(﹣1,0),
∴==,AE=1,EO=2,BE=3,
∴==,
∴=,
解得:AF=,
∴EF=,
∴FO=2﹣=,
∵=,
解得:B′F=4,
则点B′的坐标为:(,﹣4).
故答案为:(,﹣4).
19.解:∵由已知条件可知false∽false
∴false.
20.解:(1)如图所示:
;
(2)如图所示:
;
(3)如图所示:
△CC1C2的面积为×3×6=9.
21.解:∵四边形ABCD和四边形false位似,
∴四边形ABCD∽四边形false.
∵四边形false和四边形false位似,
∴四边形false∽四边形false.
∴四边形false∽四边形ABCD.
∵对应顶点的连线过同一点,
∴四边形false和四边形ABCD是位似图形.
∵四边形ABCD和四边形false位似,位似比false=2,
四边形false和四边形false位似,位似比false=1,
∴四边形false和四边形ABCD的位似比为false.
22.解:(1))△ABC与△A1B1C1的位似比等于=;
(2)如图所示
(3)△A3B3C3是由△A2B2C2沿x轴向左平移2个单位,再沿y轴向上平移2个单位得到;
(4)点P(x,y)为△ABC内一点,依次经过上述三次变换后,点P的对应点的坐标为(﹣2x﹣2,2y+2).
故答案为:;(﹣2x﹣2,2y+2).
23.解:(1)如图所示:△A1B1C1,即为所求,
C1点坐标为:(3,2);
(2)如图所示:△A2B2C2,即为所求,
C2点坐标为:(﹣6,4);
(3)如果点D(a,b)在线段AB上,经过(2)的变化后D的对应点D2的坐标为:(2a,2b).
24.解:(1)如图,线段BB1的中点即为点E,
∵B(1,1),B1(﹣1,﹣3)
∴E(0,﹣1);
(2)如图,
∵点P(a,b)是△ABC边AB上一点,△ABC经过平移后点P的对应点P′的坐标为(a﹣6,b+2),
又∵A(3,2),C(4,0),
∴A2(﹣3,4),C2(﹣2,2);
(3)∵对应顶点A1A2与B1B2的连线交于点(﹣3,0),
∴F(﹣3,0).
25.解:经测量,OA=2cm,OA′=1cm,OB=3cm,OB′=1.5cm,OC=3cm,OC′=1.5cm,
可以得到,===2,
∴A′B′∥AB,A′C′∥AC,C′B′∥CB,即位似图形的对应边互相平行,
任意改变△ABC的位置,得到△A'B′C′,△ABC与△A'B′C′的对应边互相平行,
即意改变△ABC的位置,得出的结论仍然成立.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
