2020-2021学年安徽蚌埠九年级上数学第二次月考试卷 (word版 含解析)
文档属性
| 名称 | 2020-2021学年安徽蚌埠九年级上数学第二次月考试卷 (word版 含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 574.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-18 00:00:00 | ||
图片预览

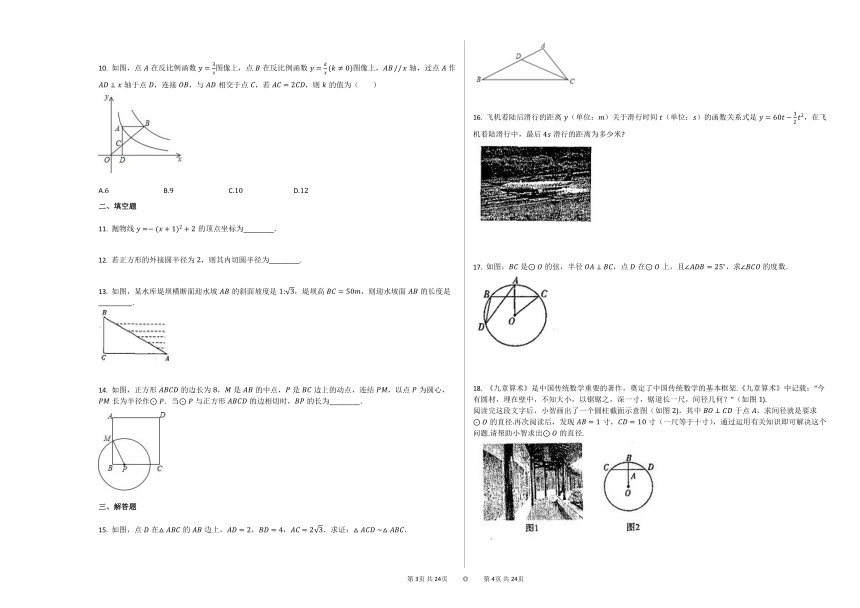



文档简介
安徽蚌埠九年级上数学月考试卷
一、选择题
?
1. 下列交通标志中,不是中心对称图形的是(? ? ? ? )
A. B. C. D.
?
2. 在平面直角坐标系中,点P坐标为(3,?-2),把线段OP绕坐标原点O顺时针旋转90?后,得到线段OQ,则点Q的坐标是(? ? ? ? )
A.(2,?3) B.(-3,?-2) C.(-3,?2) D.(-2,?-3)
?
3. 如图,⊙O的弦AB垂直平分半径OC,垂足为D.?若CD=2,则AB的长为(? ? ? ? )
A.4 B.42 C.43 D.8
?
4. 如图,圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影的示意图. 已知桌面的直径为1.2米,桌面离地面1米. 若灯泡距离地面3米,则地面上阴影部分的面积为(? ? ? ? )
A.0.36π平方米 B.0.81π平方米 C.2π平方米 D.3.24π平方米
?
5. 如图,∠AOB=100?,点C在⊙O上,且点C不与A,B重合,则∠ACB的度数为(? ? ? ? )
A.50? B.80?或50? C.130? D.50?或130?
?
6. 已知二次函数y=x2-6x+m的最小值是1,那么m的值等于(? ? ? ? )
A.1 B.10 C.4 D.6
?
7. 如图,为了测量河岸A,B两点间的距离,在与AB垂直的方向上取点C,测得AC=a,∠ABC=α,那么AB等于(? ? ? ? )
A.a?sinα B.a?cosα C.a?tanα D.atanα
?
8. 如图,AB为 ⊙O 的切线,AC,BD分别与 ⊙O 切于C,D两点.若 AB=5,AC=3?,则BD的长是(? ? ? ? )
A.2 B.3 C.4 D.5
?
9. 如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD,BE,CE,若∠CBD=33?,则∠BEC=(? ? ? ? )
A.66? B.114? C.123? D.132?
?
10. 如图,点A在反比例函数y=3x图像上,点B在反比例函数y=kx(k≠0)图像上,AB?//?x轴,过点A作AD⊥x轴于点D,连接OB,与AD相交于点C,若AC=2CD,则k的值为(? ? ? ? )
?
A.6 B.9 C.10 D.12
二、填空题
?
11. 抛物线y=-(x+1)2+2的顶点坐标为________.
?
12. 若正方形的外接圆半径为2,则其内切圆半径为________.
?
13. 如图,某水库堤坝横断面迎水坡AB的斜面坡度是1:3,堤坝高BC=50m,则迎水坡面AB的长度是_________.
?
14. 如图,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连结PM,以点P为圆心,PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时,BP的长为________.
三、解答题
?
15. 如图,点D在△ABC的AB边上,AD=2,BD=4,AC=23.求证:△ACD?△ABC.
?
16. 飞机着陆后滑行的距离y(单位:m)关于滑行时间t(单位:s)的函数关系式是y=60t-32t2,在飞机着陆滑行中,最后4s滑行的距离为多少米?
?
17. 如图,BC是⊙O的弦,半径OA⊥BC,点D在⊙O上,且∠ADB=25?,求∠BCO的度数.
?
18. 《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架.《九章算术》中记载:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,间径几何?”(如图1).
阅读完这段文字后,小智画出了一个圆柱截面示意图(如图2),其中BO⊥CD于点A,求间径就是要求⊙O的直径.再次阅读后,发现AB=1寸,CD=10寸(一尺等于十寸),通过运用有关知识即可解决这个问题.请帮助小智求出⊙O的直径.
?
19. 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,?5),B(-2,?1),C(-1,?3).
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,?0),写出顶点A1,B1的坐标,画出△A1B1C1;
(2)若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
(3)将△ABC绕点O按顺时针方向旋转90?,得到△A3B3C3,写出△A3B3C3的各顶点的坐标.
?
20. 如图,一次函数y=kx+b与反比例函数y=mx的图象交于A(2,?3),B(-3,?n)两点.
(1)求一次函数与反比例函数的表达式;
(2)根据所给条件,请直接写出不等式kx+b
(3)过点B作BC⊥x轴,垂足为C,求S△ABC.
?
21. 如图,AB是⊙O的直径,PA是⊙O的切线,A是切点,BP与⊙O交于点C.
(1)若AB=4,∠ABP=60?,求CP的长;
(2)若CD是⊙O的切线,求证:D是AP的中点.
?
22. 如图,?△ABC?为锐角三角形,过A作?DE//BC?,分别延长AC,EB交于点O;AO与DF交于点C,且?∠BCF=∠EAB?,延长FC交DE于点D,连接OD.
(1)求证:①AB?//?DF;②OB2=OE?OF;
(2)若∠OBC=∠ODC,求证:四边形ABCD为菱形.
?
23. 新华书店正在销售一种课外读本,进价12元/本,售价20元/本,为了促销,书店决定凡是一次购买10本以上的客户,每多买一本,售价就降低0.10元(顾客所购买的全部课外读本),但最低价为16元/本.
(1)问:客户一次至少买多少本,才能以最低价购买?
(2)写出当一次购买x本时(x>10),书店利润y(元)与购买量x(本)之间的函数关系式;
(3)在销售过程中,书店发现卖出50本比卖出46本赚的钱少,为了使每次的销售均能达到多卖出就多获利,在其他促销条件不变的情况下,最低价应确定为多少元/本?请说明理由.
参考答案与试题解析
2019-2020学年安徽蚌埠九年级上数学月考试卷
一、选择题
1.
【答案】
A
【考点】
中心对称图形
【解析】
根据中心对称图形的定义可直接选出答案.
【解答】
解:中心对称图形即绕对称中心旋转180?后与原图重合的图形,
观察选项,只有A项不是中心对称图形.
故选A.
2.
【答案】
D
【考点】
坐标与图形变化-旋转
【解析】
抓住旋转的三要素:旋转中心是O,旋转方向顺时针,旋转角度90?,通过画图得Q点.
【解答】
解:如图,
∵ 线段OP绕原点O顺时针旋转90?得到OQ,
∴ Q即为所求,
∴ 点Q的坐标是:(-2,?-3).
故选D.
3.
【答案】
C
【考点】
垂径定理的应用
勾股定理
【解析】
此题暂无解析
【解答】
解:连接OA.
∵ ⊙O的弦AB垂直平分半径OC,CD=2,
∴ OD=CD=2,OA=4.
在△AOD中,
AO2=OD2+AD2,
即42=22+AD2,
解得:AD=23.
由垂径定理得AB=43.
故选C.
4.
【答案】
B
【考点】
相似图形
【解析】
解答此题的关键在于理解相似图形的相关知识,掌握形状相同,大小不一定相同(放大或缩小);判定:①平行;②两角相等;③两边对应成比例,夹角相等;④三边对应成比例.
【解答】
解:桌面离地面1米,若灯泡离地面3米,则灯泡离桌面是2米,桌面与阴影是相似图形,
设阴影部分的直径是xm,则:
1.2:x=2:3,
解得x=1.8,
所以地面上阴影部分的面积为:S=πr2=0.81πm2.
故选B.
5.
【答案】
D
【考点】
圆周角定理
【解析】
利用同弧所对的圆周角是圆心角的一半,求得圆周角的度数即可,注意点C可能在优弧上也可能在劣弧上,分两种情况讨论.
【解答】
解:如图,
当点C在劣弧上时,∠ACB=12(360?-∠AOB)
=12×(360?-100?)=130?;
当点C在优弧上时,∠AC'B=12∠AOB=12×100?=50?.
故选D.
6.
【答案】
B
【考点】
二次函数的最值
【解析】
将二次函数化为顶点式,即可建立关于m的等式,解方程求出m的值即可.
【解答】
解:原式可化为:y=(x-3)2-9+m,
∵ 函数的最小值是1,
∴ -9+m=1,
m=10.
故选B.
7.
【答案】
D
【考点】
解直角三角形的应用
【解析】
根据已知角的正切值表示即可.
【解答】
解:∵ AC=a,∠ABC=α,
在直角△ABC中,tanα=ACAB,
∴ AB=atanα.
故选D.
8.
【答案】
A
【考点】
切线的性质
【解析】
此题暂无解析
【解答】
解:∵ AC,AB为⊙O的切线,
∴ AC=AE,
同理,BD=BE,
则AB=AE+BE=AC+BD=5,
∴ BD=5-AC=5-3=2.
故选A.
9.
【答案】
C
【考点】
圆周角定理
三角形的内切圆与内心
【解析】
根据圆周角定理可求∠CAD=32?,再根据三角形内心的定义可求∠BAC,再根据三角形内角和定理和三角形内心的定义可求∠EBC+∠ECB,再根据三角形内角和定理可求∠BEC的度数.
【解答】
解:在⊙O中,∵ ∠CBD=33?,
∴ ∠CAD=33?.
∵ 点E是△ABC的内心,
∴ ∠BAC=66?,
∴ ∠EBC+∠ECB=(180?-66?)÷2=57?,
∴ ∠BEC=180?-57?=123?.
故选C.
10.
【答案】
B
【考点】
矩形的性质
反比例函数综合题
反比例函数图象上点的坐标特征
反比例函数系数k的几何意义
【解析】
过点B作BE⊥x轴于E,延长线段BA,交y轴于F,得出四边形AFOD是矩形,四边形OEBF是矩形,得出S矩形AFOD=3,S矩形OEBF=k,根据平行线分线段成比例定理证得AB=2OD,即OE=3OD,即可求得矩形OEBF的面积,根据反比例函数系数k的几何意义即可求得k的值.
【解答】
解:过点B作BE⊥x轴于E,延长线段BA,交y轴于F,
∵ AB?//?x轴,
∴ AF⊥y轴,
∴ 四边形AFOD是矩形,四边形OEBF是矩形,
∴ AF=OD,BF=OE,
∴ AB=DE,
∵ 点A在双曲线y=3x上,
∴ S矩形AFOD=3,
同理S矩形OEBF=k,
∵ AB?//?OD,
∴ ODAB=CDAC=12,
∴ AB=2OD,
∴ DE=2OD,
∴ S矩形OEBF=3S矩形AFOD=9,
∴ k=9.
故选B.
二、填空题
11.
【答案】
(-1,?2)
【考点】
二次函数的性质
【解析】
根据顶点式的特点可直接写出顶点坐标.
【解答】
解:因为y=-(x+1)2+2是抛物线的顶点式,
所以根据顶点式的坐标特点可知,顶点坐标为(-1,?2).
故答案为:(-1,?2).
12.
【答案】
2
【考点】
圆内接四边形的性质
【解析】
根据题意画出图形,再由正方形及等腰直角三角形的性质求解即可.
【解答】
解:如图所示,连接OA,OB,OE,
∵ AB是小圆的切线,
∴ OE⊥AB,
∵ 四边形ABCD是正方形,OA=OB,
∴ AE=OE,
∴ △AOE是等腰直角三角形,
∴ OE=22OA=22×2=2.
故答案为:2.
13.
【答案】
100m
【考点】
解直角三角形的应用-坡度坡角问题
【解析】
根据迎水坡AB的斜面坡度是1:3,堤坝高BC=50m,可以求得AC的长,然后根据勾股定理即可得到AB的长.
【解答】
解:∵ 迎水坡AB的斜面坡度是1:3,堤坝高BC=50m,
∴ tanA=BCAC=50AC=13,
解得,AC=503,
∴ AB=AC2+BC2=(503)2+502=100(m).
故答案为:100m.
14.
【答案】
3或43
【考点】
切线的性质
正方形的性质
矩形的性质
勾股定理
【解析】
本题考查切线的性质、正方形的性质、勾股定理等知识,解题的关键是学会用分类讨论的思想思考问题,学会利用参数构建方程解决问题.
【解答】
解:①当⊙P与直线CD相切时,如图:
设PC=PM=x,
∵ 正方形ABCD的边长为8,M是AB的中点,
∴ BM=12×8=4,BP=BC-PC=8-x,∠B=90?,
在Rt△PBM中,∵ BP2+BM2=PM2,
∴ (8-x)2+42=x2,解得 x=5,
∴ BP=8-5=3;
②当⊙P 与直线AD相切时,设切点为K,连接PK,如图:
则PK⊥AD,PK=PM,∴ ∠PKD=90?,
∵ 正方形ABCD的边长为8,M是AB的中点,
∴ BM=12×8=4,?CD=8,
∠ABC=∠ADC=∠BCD=90?,
∴ 四边形PKDC是矩形,
∴ PK=CD=8,
∴ PM=PK=8,
∴ BP=PM2-BM2=43.
综上所述,BP的长为3或 43.
故答案为:3或 43.
三、解答题
15.
【答案】
证明:∵ ADAC=223=33,ACAB=33,
∴ ADAC=ACAB.
∵ ∠A=∠A,
∴ △ACD?△ABC.
【考点】
相似三角形的判定
【解析】
首先利用已知得出ADAC=ACAB,进而利用相似三角形的判定方法得出即可.
【解答】
证明:∵ ADAC=223=33,ACAB=33,
∴ ADAC=ACAB.
∵ ∠A=∠A,
∴ △ACD?△ABC.
16.
【答案】
解:∵ y=60t-32t2=-32(t-20)2+600,
a=-32<0,
∴ 当 t=20时,y有最大值600.
即:飞机着陆滑行20秒时停止滑动,此时共滑行了600米;
当t=16时,y=-32(16-20)2+600=-24+600=576,
∴ 600-576=24.
答:在飞机着陆滑行中,最后4s滑行的距离为24米.
【考点】
二次函数的应用
【解析】
此题暂无解析
【解答】
解:∵ ?y=60t-32t2=-32(t-20)2+600,
a=-32<0,
∴ 当?t=20时,y有最大值600.
即:飞机着陆滑行20秒时停止滑动,此时共滑行了600米;
当t=16时,y=-32(16-20)2+600=-24+600=576,
∴ 600-576=24.
答:在飞机着陆滑行中,最后4s滑行的距离为24米.
17.
【答案】
解:连接OB,如图,
∵ BC⊥OA,
∴ AB=AC,
∴ ∠AOB=∠AOC,
∴ ∠AOC=2∠ADB=2×25?=50?,
∴ ∠BCO=90?-50?=40?.
【考点】
圆周角定理
垂径定理
【解析】
先根据垂径定理得到AB=AC,然后根据圆周角定理求解.
【解答】
解:连接OB,如图,
∵ BC⊥OA,
∴ AB=AC,
∴ ∠AOB=∠AOC,
∴ ∠AOC=2∠ADB=2×25?=50?,
∴ ∠BCO=90?-50?=40?.
18.
【答案】
解:连接OC,
∵ BO⊥CD,垂足为A,
∴ CA=12CD=5,
设CO=x,则AO=x-1,
在Rt△AOC中,∠CAO=90?,
∴ OA2+CA2=OC2,
∴ (x-1)2+52=x2,解得x=13,
∴ ⊙O的直径为26寸.
【考点】
垂径定理的应用
勾股定理
【解析】
此题暂无解析
【解答】
解:连接OC,
∵ BO⊥CD,垂足为A,
∴ CA=12CD=5,
设CO=x,则AO=x-1,
在Rt△AOC中,∠CAO=90?,
∴ OA2+CA2=OC2,
∴ (x-1)2+52=x2,解得x=13,
∴ ⊙O的直径为26寸.
19.
【答案】
解:(1)如图,△A1B1C1即为所作,
因为点C(-1,?3)平移后的对应点C1的坐标为(4,?0),
所以△ABC先向右平移5个单位,再向下平移3个单位得到△A1B1C1,
所以点A1的坐标为(2,?2),B1点的坐标为(3,?-2);
(2)因为△ABC和△A2B2C2关于原点O成中心对称图形,
所以A2(3,?-5),B2(2,?-1),C2(1,?-3);
(3)如(1)中图,△A3B3C3即为所作,
则A3(5,?3),B3(1,?2),C3(3,?1).
【考点】
坐标与图形变化-旋转
关于原点对称的点的坐标
坐标与图形变化-平移
点的坐标
【解析】
(1)利用点C和点C1的坐标变化得到平移的方向与距离,然后利用此平移规律写出顶点A1,B1的坐标;
(2)根据关于原点对称的点的坐标特征求解;
(3)利用网格和旋转的性质画出△A2B3C3,然后写出△A2B3C3的各顶点的坐标.
【解答】
解:(1)如图,△A1B1C1即为所作,
因为点C(-1,?3)平移后的对应点C1的坐标为(4,?0),
所以△ABC先向右平移5个单位,再向下平移3个单位得到△A1B1C1,
所以点A1的坐标为(2,?2),B1点的坐标为(3,?-2);
(2)因为△ABC和△A2B2C2关于原点O成中心对称图形,
所以A2(3,?-5),B2(2,?-1),C2(1,?-3);
(3)如(1)中图,△A3B3C3即为所作,
则A3(5,?3),B3(1,?2),C3(3,?1).
20.
【答案】
解:(1)把点A(2,?3)代入y=mx得:m=2×3=6,
∴ 反比例函数表达式为y=6x,
把B(-3,?n)代入y=6x得:n=-2,即B(-3,?-2),
把A(2,?3),B(-3,?-2)代入y=kx+b得:
2k+b=3,-3k+b=-2,?
解得:k=1,b=1,
∴ 一次函数表达式为y=x+1;
(2)由图象知:当x<-3或0(3)根据题意得:
S△ABC=12×2×(2+3)=5.
【考点】
反比例函数与一次函数的综合
待定系数法求一次函数解析式
三角形的面积
待定系数法求反比例函数解析式
【解析】
(1)把A坐标代入反比例解析式求出m的值,确定出反比例解析式,将B坐标代入求出n的值,确定出B坐标,将A与B坐标代入一次函数解析式求出k与b的值即可;
(2)利用图象找出所求不等式的解集即可;
(3)以BC为底,A与B横坐标相减为高求出三角形面积即可.
【解答】
解:(1)把点A(2,?3)代入y=mx得:m=2×3=6,
∴ 反比例函数表达式为y=6x,
把B(-3,?n)代入y=6x得:n=-2,即B(-3,?-2),
把A(2,?3),B(-3,?-2)代入y=kx+b得:
2k+b=3,-3k+b=-2,?
解得:k=1,b=1,
∴ 一次函数表达式为y=x+1;
(2)由图象知:当x<-3或0(3)根据题意得:
S△ABC=12×2×(2+3)=5.
21.
【答案】
(1)解:如图,连接AC.
∵ PA是⊙O的切线,AB是直径,
∴ PA⊥AB,
∴ ∠BAP=90?,
∴ ∠P+∠ABP=90?.
∵ ∠ABP=60?,
∴ ∠P=30?.
又∵ AB=4,∴ PB=2AB=2×4=8.
∵ AB是直径,
∴ ∠BCA=90?,
∴ ∠BAC=30?,
∴ BC=12AB=2,
∴ PC=PB-BC=6;
(2)证明:如图,连接OC.
∵ PA是⊙O的切线,CD是⊙O的切线,
∴ ∠OAC+∠DAC=90?,∠DCA+∠OCA=90?.
∵ OA=OC,∴ ∠OAC=∠OCA,
∴ ∠DAC=∠DCA,∴ CD=AD.
∵ CD是⊙O的切线,
∴ ∠CAP+∠P=∠DCA+∠PCD=90?,
∴ ∠P=∠PCD,
∴ CD=PD,
∴ D是AP的中点.
【考点】
圆周角定理
切线的性质
【解析】
(1)首先根据切线的性质判定∠BAP=90?;然后在直角三角形ABP中利用三角函数的定义求得AP的长度;
【解答】
(1)解:如图,连接AC.
∵ PA是⊙O的切线,AB是直径,?
∴ PA⊥AB,
∴ ∠BAP=90?,
∴ ∠P+∠ABP=90?.
∵ ∠ABP=60?,
∴ ∠P=30?.
又∵ AB=4,∴ PB=2AB=2×4=8.
∵ AB是直径,
∴ ∠BCA=90?,
∴ ∠BAC=30?,
∴ BC=12AB=2,
∴ PC=PB-BC=6;
(2)证明:如图,连接OC.
∵ PA是⊙O的切线,CD是⊙O的切线,
∴ ∠OAC+∠DAC=90?,∠DCA+∠OCA=90?.
∵ OA=OC,∴ ∠OAC=∠OCA,
∴ ∠DAC=∠DCA,∴ CD=AD.
∵ CD是⊙O的切线,
∴ ∠CAP+∠P=∠DCA+∠PCD=90?,
∴ ∠P=∠PCD,
∴ CD=PD,
∴ D是AP的中点.
22.
【答案】
证明:(1)①∵ DE?//?BC,
∴ ∠EDF=∠BCF,
∵ ∠EAB=∠BCF,
∴ ∠EAB=∠EDF,
∴ AB?//?DF.
②∵ DE?//?BC,
∴ OBOE=OCOA,
∵ AB?//?CD,
∴ OCOA=OFOB,
∴ OBOE=OFOB,
∴ OB2=OE?OF.
(2)连接BD交AO于点P,
∵ DE?//?BC,
∴ ∠OBC=∠E,
∵ ∠OBC=∠ODC,
∴ ∠ODC=∠E,
∵ ∠DOF=∠DOE,
∴ △ODF?△OED,
∴ ODOE=OFOD,
∴ OD2=OE?OF,
∵ OB2=OE?OF,
∴ OB=OD,
∵ DE?//?BC,AB?//?DF,
∴ 四边形ABCD是平行四边形,
∴ BP=DP,
∴ OP⊥BD,
∴ 四边形ABCD是菱形.
【考点】
相似三角形的性质与判定
平行线分线段成比例
菱形的判定
【解析】
(1)欲证明AB?//?DF,只要证明∠EAB=∠EDF即可;
(2)由DE?//?BC,可得OBOE=OCOA,由AB?//?CD,可得OCOA=OFOB,即可推出OBOE=OFOB,由此即可解决问题;
(3)首先证明OB=OD,再证明四边形ABCD是平行四边形,BD⊥AC即可解决问题;
【解答】
证明:(1)①∵ DE?//?BC,
∴ ∠EDF=∠BCF,
∵ ∠EAB=∠BCF,
∴ ∠EAB=∠EDF,
∴ AB?//?DF.
②∵ DE?//?BC,
∴ OBOE=OCOA,
∵ AB?//?CD,
∴ OCOA=OFOB,
∴ OBOE=OFOB,
∴ OB2=OE?OF.
(2)连接BD交AO于点P,
∵ DE?//?BC,
∴ ∠OBC=∠E,
∵ ∠OBC=∠ODC,
∴ ∠ODC=∠E,
∵ ∠DOF=∠DOE,
∴ △ODF?△OED,
∴ ODOE=OFOD,
∴ OD2=OE?OF,
∵ OB2=OE?OF,
∴ OB=OD,
∵ DE?//?BC,AB?//?DF,
∴ 四边形ABCD是平行四边形,
∴ BP=DP,
∴ OP⊥BD,
∴ 四边形ABCD是菱形.
23.
【答案】
解:(1)设客户一次购买x本,才能以最低价购买,
由题意得,(x-10)×0.1=20-16,解得:x=50,
答:客户一次至少买50本,才能以最低价购买.
(2)当10y=[20-12-0.1(x-10)]?x=-0.1x2+9x,
当x>50时,y=(16-12)?x=4x,
即y=-0.1x2+9x(1050).
(3)当10y=-0.1x2+9x=-0.1(x2-90x)=-0.1(x-45)2+202.5,
因为-0.1<0,
所以当x=45时,y最大=202.5,
当45所以,卖出50本比卖出46本赚的钱少,
因此最低价定在销售数量为45本时的价格,
才能使每次的销售均能达到多卖出就多获利,
20-0.1×(45-10)=20-3.5=16.5(元),
即最低价应确定为16.5元/本.
【考点】
一元一次方程的应用——其他问题
二次函数的应用
【解析】
(1)设客户一次购买x本,才能以最低价购买,然后根据降低的价钱列出方程求解即可;
(2)根据利润等于每本的盈利乘以购买的本数,分大于最低价与等于最低价两种情况列式整理即可得解;
(3)根据二次函数的最值问题确定出获利最多时卖出书本的本数即可得解.
【解答】
解:(1)设客户一次购买x本,才能以最低价购买,
由题意得,(x-10)×0.1=20-16,解得:x=50,
答:客户一次至少买50本,才能以最低价购买.
(2)当10y=[20-12-0.1(x-10)]?x=-0.1x2+9x,
当x>50时,y=(16-12)?x=4x,
即y=-0.1x2+9x(1050).
(3)当10y=-0.1x2+9x=-0.1(x2-90x)=-0.1(x-45)2+202.5,
因为-0.1<0,
所以当x=45时,y最大=202.5,
当45所以,卖出50本比卖出46本赚的钱少,
因此最低价定在销售数量为45本时的价格,
才能使每次的销售均能达到多卖出就多获利,
20-0.1×(45-10)=20-3.5=16.5(元),
即最低价应确定为16.5元/本.
一、选择题
?
1. 下列交通标志中,不是中心对称图形的是(? ? ? ? )
A. B. C. D.
?
2. 在平面直角坐标系中,点P坐标为(3,?-2),把线段OP绕坐标原点O顺时针旋转90?后,得到线段OQ,则点Q的坐标是(? ? ? ? )
A.(2,?3) B.(-3,?-2) C.(-3,?2) D.(-2,?-3)
?
3. 如图,⊙O的弦AB垂直平分半径OC,垂足为D.?若CD=2,则AB的长为(? ? ? ? )
A.4 B.42 C.43 D.8
?
4. 如图,圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影的示意图. 已知桌面的直径为1.2米,桌面离地面1米. 若灯泡距离地面3米,则地面上阴影部分的面积为(? ? ? ? )
A.0.36π平方米 B.0.81π平方米 C.2π平方米 D.3.24π平方米
?
5. 如图,∠AOB=100?,点C在⊙O上,且点C不与A,B重合,则∠ACB的度数为(? ? ? ? )
A.50? B.80?或50? C.130? D.50?或130?
?
6. 已知二次函数y=x2-6x+m的最小值是1,那么m的值等于(? ? ? ? )
A.1 B.10 C.4 D.6
?
7. 如图,为了测量河岸A,B两点间的距离,在与AB垂直的方向上取点C,测得AC=a,∠ABC=α,那么AB等于(? ? ? ? )
A.a?sinα B.a?cosα C.a?tanα D.atanα
?
8. 如图,AB为 ⊙O 的切线,AC,BD分别与 ⊙O 切于C,D两点.若 AB=5,AC=3?,则BD的长是(? ? ? ? )
A.2 B.3 C.4 D.5
?
9. 如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD,BE,CE,若∠CBD=33?,则∠BEC=(? ? ? ? )
A.66? B.114? C.123? D.132?
?
10. 如图,点A在反比例函数y=3x图像上,点B在反比例函数y=kx(k≠0)图像上,AB?//?x轴,过点A作AD⊥x轴于点D,连接OB,与AD相交于点C,若AC=2CD,则k的值为(? ? ? ? )
?
A.6 B.9 C.10 D.12
二、填空题
?
11. 抛物线y=-(x+1)2+2的顶点坐标为________.
?
12. 若正方形的外接圆半径为2,则其内切圆半径为________.
?
13. 如图,某水库堤坝横断面迎水坡AB的斜面坡度是1:3,堤坝高BC=50m,则迎水坡面AB的长度是_________.
?
14. 如图,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连结PM,以点P为圆心,PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时,BP的长为________.
三、解答题
?
15. 如图,点D在△ABC的AB边上,AD=2,BD=4,AC=23.求证:△ACD?△ABC.
?
16. 飞机着陆后滑行的距离y(单位:m)关于滑行时间t(单位:s)的函数关系式是y=60t-32t2,在飞机着陆滑行中,最后4s滑行的距离为多少米?
?
17. 如图,BC是⊙O的弦,半径OA⊥BC,点D在⊙O上,且∠ADB=25?,求∠BCO的度数.
?
18. 《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架.《九章算术》中记载:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,间径几何?”(如图1).
阅读完这段文字后,小智画出了一个圆柱截面示意图(如图2),其中BO⊥CD于点A,求间径就是要求⊙O的直径.再次阅读后,发现AB=1寸,CD=10寸(一尺等于十寸),通过运用有关知识即可解决这个问题.请帮助小智求出⊙O的直径.
?
19. 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,?5),B(-2,?1),C(-1,?3).
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,?0),写出顶点A1,B1的坐标,画出△A1B1C1;
(2)若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
(3)将△ABC绕点O按顺时针方向旋转90?,得到△A3B3C3,写出△A3B3C3的各顶点的坐标.
?
20. 如图,一次函数y=kx+b与反比例函数y=mx的图象交于A(2,?3),B(-3,?n)两点.
(1)求一次函数与反比例函数的表达式;
(2)根据所给条件,请直接写出不等式kx+b
(3)过点B作BC⊥x轴,垂足为C,求S△ABC.
?
21. 如图,AB是⊙O的直径,PA是⊙O的切线,A是切点,BP与⊙O交于点C.
(1)若AB=4,∠ABP=60?,求CP的长;
(2)若CD是⊙O的切线,求证:D是AP的中点.
?
22. 如图,?△ABC?为锐角三角形,过A作?DE//BC?,分别延长AC,EB交于点O;AO与DF交于点C,且?∠BCF=∠EAB?,延长FC交DE于点D,连接OD.
(1)求证:①AB?//?DF;②OB2=OE?OF;
(2)若∠OBC=∠ODC,求证:四边形ABCD为菱形.
?
23. 新华书店正在销售一种课外读本,进价12元/本,售价20元/本,为了促销,书店决定凡是一次购买10本以上的客户,每多买一本,售价就降低0.10元(顾客所购买的全部课外读本),但最低价为16元/本.
(1)问:客户一次至少买多少本,才能以最低价购买?
(2)写出当一次购买x本时(x>10),书店利润y(元)与购买量x(本)之间的函数关系式;
(3)在销售过程中,书店发现卖出50本比卖出46本赚的钱少,为了使每次的销售均能达到多卖出就多获利,在其他促销条件不变的情况下,最低价应确定为多少元/本?请说明理由.
参考答案与试题解析
2019-2020学年安徽蚌埠九年级上数学月考试卷
一、选择题
1.
【答案】
A
【考点】
中心对称图形
【解析】
根据中心对称图形的定义可直接选出答案.
【解答】
解:中心对称图形即绕对称中心旋转180?后与原图重合的图形,
观察选项,只有A项不是中心对称图形.
故选A.
2.
【答案】
D
【考点】
坐标与图形变化-旋转
【解析】
抓住旋转的三要素:旋转中心是O,旋转方向顺时针,旋转角度90?,通过画图得Q点.
【解答】
解:如图,
∵ 线段OP绕原点O顺时针旋转90?得到OQ,
∴ Q即为所求,
∴ 点Q的坐标是:(-2,?-3).
故选D.
3.
【答案】
C
【考点】
垂径定理的应用
勾股定理
【解析】
此题暂无解析
【解答】
解:连接OA.
∵ ⊙O的弦AB垂直平分半径OC,CD=2,
∴ OD=CD=2,OA=4.
在△AOD中,
AO2=OD2+AD2,
即42=22+AD2,
解得:AD=23.
由垂径定理得AB=43.
故选C.
4.
【答案】
B
【考点】
相似图形
【解析】
解答此题的关键在于理解相似图形的相关知识,掌握形状相同,大小不一定相同(放大或缩小);判定:①平行;②两角相等;③两边对应成比例,夹角相等;④三边对应成比例.
【解答】
解:桌面离地面1米,若灯泡离地面3米,则灯泡离桌面是2米,桌面与阴影是相似图形,
设阴影部分的直径是xm,则:
1.2:x=2:3,
解得x=1.8,
所以地面上阴影部分的面积为:S=πr2=0.81πm2.
故选B.
5.
【答案】
D
【考点】
圆周角定理
【解析】
利用同弧所对的圆周角是圆心角的一半,求得圆周角的度数即可,注意点C可能在优弧上也可能在劣弧上,分两种情况讨论.
【解答】
解:如图,
当点C在劣弧上时,∠ACB=12(360?-∠AOB)
=12×(360?-100?)=130?;
当点C在优弧上时,∠AC'B=12∠AOB=12×100?=50?.
故选D.
6.
【答案】
B
【考点】
二次函数的最值
【解析】
将二次函数化为顶点式,即可建立关于m的等式,解方程求出m的值即可.
【解答】
解:原式可化为:y=(x-3)2-9+m,
∵ 函数的最小值是1,
∴ -9+m=1,
m=10.
故选B.
7.
【答案】
D
【考点】
解直角三角形的应用
【解析】
根据已知角的正切值表示即可.
【解答】
解:∵ AC=a,∠ABC=α,
在直角△ABC中,tanα=ACAB,
∴ AB=atanα.
故选D.
8.
【答案】
A
【考点】
切线的性质
【解析】
此题暂无解析
【解答】
解:∵ AC,AB为⊙O的切线,
∴ AC=AE,
同理,BD=BE,
则AB=AE+BE=AC+BD=5,
∴ BD=5-AC=5-3=2.
故选A.
9.
【答案】
C
【考点】
圆周角定理
三角形的内切圆与内心
【解析】
根据圆周角定理可求∠CAD=32?,再根据三角形内心的定义可求∠BAC,再根据三角形内角和定理和三角形内心的定义可求∠EBC+∠ECB,再根据三角形内角和定理可求∠BEC的度数.
【解答】
解:在⊙O中,∵ ∠CBD=33?,
∴ ∠CAD=33?.
∵ 点E是△ABC的内心,
∴ ∠BAC=66?,
∴ ∠EBC+∠ECB=(180?-66?)÷2=57?,
∴ ∠BEC=180?-57?=123?.
故选C.
10.
【答案】
B
【考点】
矩形的性质
反比例函数综合题
反比例函数图象上点的坐标特征
反比例函数系数k的几何意义
【解析】
过点B作BE⊥x轴于E,延长线段BA,交y轴于F,得出四边形AFOD是矩形,四边形OEBF是矩形,得出S矩形AFOD=3,S矩形OEBF=k,根据平行线分线段成比例定理证得AB=2OD,即OE=3OD,即可求得矩形OEBF的面积,根据反比例函数系数k的几何意义即可求得k的值.
【解答】
解:过点B作BE⊥x轴于E,延长线段BA,交y轴于F,
∵ AB?//?x轴,
∴ AF⊥y轴,
∴ 四边形AFOD是矩形,四边形OEBF是矩形,
∴ AF=OD,BF=OE,
∴ AB=DE,
∵ 点A在双曲线y=3x上,
∴ S矩形AFOD=3,
同理S矩形OEBF=k,
∵ AB?//?OD,
∴ ODAB=CDAC=12,
∴ AB=2OD,
∴ DE=2OD,
∴ S矩形OEBF=3S矩形AFOD=9,
∴ k=9.
故选B.
二、填空题
11.
【答案】
(-1,?2)
【考点】
二次函数的性质
【解析】
根据顶点式的特点可直接写出顶点坐标.
【解答】
解:因为y=-(x+1)2+2是抛物线的顶点式,
所以根据顶点式的坐标特点可知,顶点坐标为(-1,?2).
故答案为:(-1,?2).
12.
【答案】
2
【考点】
圆内接四边形的性质
【解析】
根据题意画出图形,再由正方形及等腰直角三角形的性质求解即可.
【解答】
解:如图所示,连接OA,OB,OE,
∵ AB是小圆的切线,
∴ OE⊥AB,
∵ 四边形ABCD是正方形,OA=OB,
∴ AE=OE,
∴ △AOE是等腰直角三角形,
∴ OE=22OA=22×2=2.
故答案为:2.
13.
【答案】
100m
【考点】
解直角三角形的应用-坡度坡角问题
【解析】
根据迎水坡AB的斜面坡度是1:3,堤坝高BC=50m,可以求得AC的长,然后根据勾股定理即可得到AB的长.
【解答】
解:∵ 迎水坡AB的斜面坡度是1:3,堤坝高BC=50m,
∴ tanA=BCAC=50AC=13,
解得,AC=503,
∴ AB=AC2+BC2=(503)2+502=100(m).
故答案为:100m.
14.
【答案】
3或43
【考点】
切线的性质
正方形的性质
矩形的性质
勾股定理
【解析】
本题考查切线的性质、正方形的性质、勾股定理等知识,解题的关键是学会用分类讨论的思想思考问题,学会利用参数构建方程解决问题.
【解答】
解:①当⊙P与直线CD相切时,如图:
设PC=PM=x,
∵ 正方形ABCD的边长为8,M是AB的中点,
∴ BM=12×8=4,BP=BC-PC=8-x,∠B=90?,
在Rt△PBM中,∵ BP2+BM2=PM2,
∴ (8-x)2+42=x2,解得 x=5,
∴ BP=8-5=3;
②当⊙P 与直线AD相切时,设切点为K,连接PK,如图:
则PK⊥AD,PK=PM,∴ ∠PKD=90?,
∵ 正方形ABCD的边长为8,M是AB的中点,
∴ BM=12×8=4,?CD=8,
∠ABC=∠ADC=∠BCD=90?,
∴ 四边形PKDC是矩形,
∴ PK=CD=8,
∴ PM=PK=8,
∴ BP=PM2-BM2=43.
综上所述,BP的长为3或 43.
故答案为:3或 43.
三、解答题
15.
【答案】
证明:∵ ADAC=223=33,ACAB=33,
∴ ADAC=ACAB.
∵ ∠A=∠A,
∴ △ACD?△ABC.
【考点】
相似三角形的判定
【解析】
首先利用已知得出ADAC=ACAB,进而利用相似三角形的判定方法得出即可.
【解答】
证明:∵ ADAC=223=33,ACAB=33,
∴ ADAC=ACAB.
∵ ∠A=∠A,
∴ △ACD?△ABC.
16.
【答案】
解:∵ y=60t-32t2=-32(t-20)2+600,
a=-32<0,
∴ 当 t=20时,y有最大值600.
即:飞机着陆滑行20秒时停止滑动,此时共滑行了600米;
当t=16时,y=-32(16-20)2+600=-24+600=576,
∴ 600-576=24.
答:在飞机着陆滑行中,最后4s滑行的距离为24米.
【考点】
二次函数的应用
【解析】
此题暂无解析
【解答】
解:∵ ?y=60t-32t2=-32(t-20)2+600,
a=-32<0,
∴ 当?t=20时,y有最大值600.
即:飞机着陆滑行20秒时停止滑动,此时共滑行了600米;
当t=16时,y=-32(16-20)2+600=-24+600=576,
∴ 600-576=24.
答:在飞机着陆滑行中,最后4s滑行的距离为24米.
17.
【答案】
解:连接OB,如图,
∵ BC⊥OA,
∴ AB=AC,
∴ ∠AOB=∠AOC,
∴ ∠AOC=2∠ADB=2×25?=50?,
∴ ∠BCO=90?-50?=40?.
【考点】
圆周角定理
垂径定理
【解析】
先根据垂径定理得到AB=AC,然后根据圆周角定理求解.
【解答】
解:连接OB,如图,
∵ BC⊥OA,
∴ AB=AC,
∴ ∠AOB=∠AOC,
∴ ∠AOC=2∠ADB=2×25?=50?,
∴ ∠BCO=90?-50?=40?.
18.
【答案】
解:连接OC,
∵ BO⊥CD,垂足为A,
∴ CA=12CD=5,
设CO=x,则AO=x-1,
在Rt△AOC中,∠CAO=90?,
∴ OA2+CA2=OC2,
∴ (x-1)2+52=x2,解得x=13,
∴ ⊙O的直径为26寸.
【考点】
垂径定理的应用
勾股定理
【解析】
此题暂无解析
【解答】
解:连接OC,
∵ BO⊥CD,垂足为A,
∴ CA=12CD=5,
设CO=x,则AO=x-1,
在Rt△AOC中,∠CAO=90?,
∴ OA2+CA2=OC2,
∴ (x-1)2+52=x2,解得x=13,
∴ ⊙O的直径为26寸.
19.
【答案】
解:(1)如图,△A1B1C1即为所作,
因为点C(-1,?3)平移后的对应点C1的坐标为(4,?0),
所以△ABC先向右平移5个单位,再向下平移3个单位得到△A1B1C1,
所以点A1的坐标为(2,?2),B1点的坐标为(3,?-2);
(2)因为△ABC和△A2B2C2关于原点O成中心对称图形,
所以A2(3,?-5),B2(2,?-1),C2(1,?-3);
(3)如(1)中图,△A3B3C3即为所作,
则A3(5,?3),B3(1,?2),C3(3,?1).
【考点】
坐标与图形变化-旋转
关于原点对称的点的坐标
坐标与图形变化-平移
点的坐标
【解析】
(1)利用点C和点C1的坐标变化得到平移的方向与距离,然后利用此平移规律写出顶点A1,B1的坐标;
(2)根据关于原点对称的点的坐标特征求解;
(3)利用网格和旋转的性质画出△A2B3C3,然后写出△A2B3C3的各顶点的坐标.
【解答】
解:(1)如图,△A1B1C1即为所作,
因为点C(-1,?3)平移后的对应点C1的坐标为(4,?0),
所以△ABC先向右平移5个单位,再向下平移3个单位得到△A1B1C1,
所以点A1的坐标为(2,?2),B1点的坐标为(3,?-2);
(2)因为△ABC和△A2B2C2关于原点O成中心对称图形,
所以A2(3,?-5),B2(2,?-1),C2(1,?-3);
(3)如(1)中图,△A3B3C3即为所作,
则A3(5,?3),B3(1,?2),C3(3,?1).
20.
【答案】
解:(1)把点A(2,?3)代入y=mx得:m=2×3=6,
∴ 反比例函数表达式为y=6x,
把B(-3,?n)代入y=6x得:n=-2,即B(-3,?-2),
把A(2,?3),B(-3,?-2)代入y=kx+b得:
2k+b=3,-3k+b=-2,?
解得:k=1,b=1,
∴ 一次函数表达式为y=x+1;
(2)由图象知:当x<-3或0
S△ABC=12×2×(2+3)=5.
【考点】
反比例函数与一次函数的综合
待定系数法求一次函数解析式
三角形的面积
待定系数法求反比例函数解析式
【解析】
(1)把A坐标代入反比例解析式求出m的值,确定出反比例解析式,将B坐标代入求出n的值,确定出B坐标,将A与B坐标代入一次函数解析式求出k与b的值即可;
(2)利用图象找出所求不等式的解集即可;
(3)以BC为底,A与B横坐标相减为高求出三角形面积即可.
【解答】
解:(1)把点A(2,?3)代入y=mx得:m=2×3=6,
∴ 反比例函数表达式为y=6x,
把B(-3,?n)代入y=6x得:n=-2,即B(-3,?-2),
把A(2,?3),B(-3,?-2)代入y=kx+b得:
2k+b=3,-3k+b=-2,?
解得:k=1,b=1,
∴ 一次函数表达式为y=x+1;
(2)由图象知:当x<-3或0
S△ABC=12×2×(2+3)=5.
21.
【答案】
(1)解:如图,连接AC.
∵ PA是⊙O的切线,AB是直径,
∴ PA⊥AB,
∴ ∠BAP=90?,
∴ ∠P+∠ABP=90?.
∵ ∠ABP=60?,
∴ ∠P=30?.
又∵ AB=4,∴ PB=2AB=2×4=8.
∵ AB是直径,
∴ ∠BCA=90?,
∴ ∠BAC=30?,
∴ BC=12AB=2,
∴ PC=PB-BC=6;
(2)证明:如图,连接OC.
∵ PA是⊙O的切线,CD是⊙O的切线,
∴ ∠OAC+∠DAC=90?,∠DCA+∠OCA=90?.
∵ OA=OC,∴ ∠OAC=∠OCA,
∴ ∠DAC=∠DCA,∴ CD=AD.
∵ CD是⊙O的切线,
∴ ∠CAP+∠P=∠DCA+∠PCD=90?,
∴ ∠P=∠PCD,
∴ CD=PD,
∴ D是AP的中点.
【考点】
圆周角定理
切线的性质
【解析】
(1)首先根据切线的性质判定∠BAP=90?;然后在直角三角形ABP中利用三角函数的定义求得AP的长度;
【解答】
(1)解:如图,连接AC.
∵ PA是⊙O的切线,AB是直径,?
∴ PA⊥AB,
∴ ∠BAP=90?,
∴ ∠P+∠ABP=90?.
∵ ∠ABP=60?,
∴ ∠P=30?.
又∵ AB=4,∴ PB=2AB=2×4=8.
∵ AB是直径,
∴ ∠BCA=90?,
∴ ∠BAC=30?,
∴ BC=12AB=2,
∴ PC=PB-BC=6;
(2)证明:如图,连接OC.
∵ PA是⊙O的切线,CD是⊙O的切线,
∴ ∠OAC+∠DAC=90?,∠DCA+∠OCA=90?.
∵ OA=OC,∴ ∠OAC=∠OCA,
∴ ∠DAC=∠DCA,∴ CD=AD.
∵ CD是⊙O的切线,
∴ ∠CAP+∠P=∠DCA+∠PCD=90?,
∴ ∠P=∠PCD,
∴ CD=PD,
∴ D是AP的中点.
22.
【答案】
证明:(1)①∵ DE?//?BC,
∴ ∠EDF=∠BCF,
∵ ∠EAB=∠BCF,
∴ ∠EAB=∠EDF,
∴ AB?//?DF.
②∵ DE?//?BC,
∴ OBOE=OCOA,
∵ AB?//?CD,
∴ OCOA=OFOB,
∴ OBOE=OFOB,
∴ OB2=OE?OF.
(2)连接BD交AO于点P,
∵ DE?//?BC,
∴ ∠OBC=∠E,
∵ ∠OBC=∠ODC,
∴ ∠ODC=∠E,
∵ ∠DOF=∠DOE,
∴ △ODF?△OED,
∴ ODOE=OFOD,
∴ OD2=OE?OF,
∵ OB2=OE?OF,
∴ OB=OD,
∵ DE?//?BC,AB?//?DF,
∴ 四边形ABCD是平行四边形,
∴ BP=DP,
∴ OP⊥BD,
∴ 四边形ABCD是菱形.
【考点】
相似三角形的性质与判定
平行线分线段成比例
菱形的判定
【解析】
(1)欲证明AB?//?DF,只要证明∠EAB=∠EDF即可;
(2)由DE?//?BC,可得OBOE=OCOA,由AB?//?CD,可得OCOA=OFOB,即可推出OBOE=OFOB,由此即可解决问题;
(3)首先证明OB=OD,再证明四边形ABCD是平行四边形,BD⊥AC即可解决问题;
【解答】
证明:(1)①∵ DE?//?BC,
∴ ∠EDF=∠BCF,
∵ ∠EAB=∠BCF,
∴ ∠EAB=∠EDF,
∴ AB?//?DF.
②∵ DE?//?BC,
∴ OBOE=OCOA,
∵ AB?//?CD,
∴ OCOA=OFOB,
∴ OBOE=OFOB,
∴ OB2=OE?OF.
(2)连接BD交AO于点P,
∵ DE?//?BC,
∴ ∠OBC=∠E,
∵ ∠OBC=∠ODC,
∴ ∠ODC=∠E,
∵ ∠DOF=∠DOE,
∴ △ODF?△OED,
∴ ODOE=OFOD,
∴ OD2=OE?OF,
∵ OB2=OE?OF,
∴ OB=OD,
∵ DE?//?BC,AB?//?DF,
∴ 四边形ABCD是平行四边形,
∴ BP=DP,
∴ OP⊥BD,
∴ 四边形ABCD是菱形.
23.
【答案】
解:(1)设客户一次购买x本,才能以最低价购买,
由题意得,(x-10)×0.1=20-16,解得:x=50,
答:客户一次至少买50本,才能以最低价购买.
(2)当10
当x>50时,y=(16-12)?x=4x,
即y=-0.1x2+9x(10
(3)当10
因为-0.1<0,
所以当x=45时,y最大=202.5,
当45
因此最低价定在销售数量为45本时的价格,
才能使每次的销售均能达到多卖出就多获利,
20-0.1×(45-10)=20-3.5=16.5(元),
即最低价应确定为16.5元/本.
【考点】
一元一次方程的应用——其他问题
二次函数的应用
【解析】
(1)设客户一次购买x本,才能以最低价购买,然后根据降低的价钱列出方程求解即可;
(2)根据利润等于每本的盈利乘以购买的本数,分大于最低价与等于最低价两种情况列式整理即可得解;
(3)根据二次函数的最值问题确定出获利最多时卖出书本的本数即可得解.
【解答】
解:(1)设客户一次购买x本,才能以最低价购买,
由题意得,(x-10)×0.1=20-16,解得:x=50,
答:客户一次至少买50本,才能以最低价购买.
(2)当10
当x>50时,y=(16-12)?x=4x,
即y=-0.1x2+9x(10
(3)当10
因为-0.1<0,
所以当x=45时,y最大=202.5,
当45
因此最低价定在销售数量为45本时的价格,
才能使每次的销售均能达到多卖出就多获利,
20-0.1×(45-10)=20-3.5=16.5(元),
即最低价应确定为16.5元/本.
同课章节目录
