北师大版七年级数学下册 4.5利用三角形全等测距离 习题课件(共26张PPT)
文档属性
| 名称 | 北师大版七年级数学下册 4.5利用三角形全等测距离 习题课件(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 772.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 16:12:49 | ||
图片预览








文档简介
(共26张PPT)
第四章
三角形
4.5
利用三角形全等测距离
北师大版七年级数学下册
习题课件
4
提示:点击
进入习题
答案显示
6
7
1
2
3
5
SAS;BC
A
B
2.5
m
8
见习题
见习题
D
B
提示:点击
进入习题
答案显示
10
11
9
见习题
见习题
见习题
1.如图,为了测量出A,B两点之间的距离,在地面上找到一点C,连接BC,AC,使∠ACB=90°,然后在BC的延长线上确定点D,使CD=BC,那么只要测量出AD的长度也就得到了A,B两点之间的距离,这样测量的依据是( )
A.AAS
B.SAS
C.ASA
D.SSS
【点拨】因为AC⊥BD,所以∠ACB=∠ACD=90°.在△ACB和△ACD中,AC=AC,∠ACB=∠ACD,CB=CD,所以△ACB≌△ACD(SAS).所以AB=AD(全等三角形的对应边相等).
【答案】B
2.如图,A,B在一水池两侧,若BE=DE,∠B=∠D=90°,CD=10
m,则水池宽AB为( )
A.8
m
B.10
m
C.12
m
D.无法确定
B
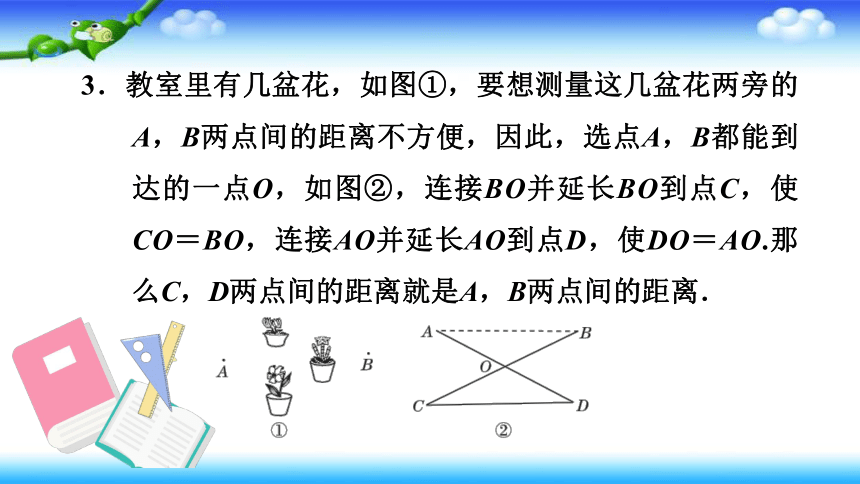
3.教室里有几盆花,如图①,要想测量这几盆花两旁的A,B两点间的距离不方便,因此,选点A,B都能到达的一点O,如图②,连接BO并延长BO到点C,使CO=BO,连接AO并延长AO到点D,使DO=AO.那么C,D两点间的距离就是A,B两点间的距离.
SAS
BA
4.如图,将两根钢条AA′,BB′的中点O连在一起,使AA′,BB′可以绕着点O自由转动,就
做成了一个测量工件,由三角形全等得出A′B′的长等于内槽宽AB,那么判定△OAB≌△OA′B′的理由是( )
A.边角边
B.角边角
C.边边边
D.角角边
A
5.如图,某校学生为测量B点到河对面的目标A之间的距离,他们在B点同侧选择了一点C,测得∠ABC=70°,∠ACB=40°,然后在M处立了标杆,使∠CBM=70°,那么他们还应做什么才能测得A,B之间的距离?( )
A.直接测量BM
B.测量BC
C.测量∠A的度数
D.作∠BCN=40°交MB于点N
【点拨】由题意知,∠ABC=∠CBM,BC为公共边,选项D符合“ASA”判定条件.
【答案】D
6.如图,有两个滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,左边滑梯水平方向的长度AB与右边滑梯的高度DE相等,测得BC=2.5
m,则EF= .
【点拨】由题意,因为左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,左边滑梯水平方向的长度AB与右边滑梯的高度DE相等,所以AC=DF,AB=DE.又因为∠BAC=∠EDF,所以△BAC≌△EDF(SAS).所以EF=BC=2.5
m.
【答案】2.5
m
7.如图是由两根钢丝固定的高压电线杆,按要求当两根钢丝与电线杆的夹角相同时,固定效果最好.现已知钢丝触地点到电线杆的距离相等,那么请你判断图中两根钢丝的固定效果是否最好,并说明理由(电线杆的粗细忽略不计).
【点拨】本题易误认为AB=AC,由BO=CO,AO=AO判定△ABO≌△ACO而出错.
8.如图,小刚站在河边的点A处,在河的对面(小刚的正北方向)的点B处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树点C处,接着再向前走了30步到达点D处,然后他左转90°直行,当小刚看到电线塔、树与自己现处的位置E在一条直线上时,
他共走了140步.
(1)根据题意,画出示意图;
解:所画示意图如图所示.
(2)如果小刚一步大约50
cm,估计小刚在点A处时他与电线塔的距离,并说明理由.
9.【2019·南通】如图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A和B.连接AC并延长到点D,使CD=CA.连接BC并延长到点E,使CE=CB.连接DE,那么量出DE的长就是A,B的距离.为什么?
10.如图,某市新开发了一个旅游景点,湖心有一个小岛C,现需要在湖心小岛C上修建一个度假村,因此要测量景点A,B与C的距离.设计人员拟出下列方案:画出∠BAM=∠CAB,∠ABN=∠ABC,射线AM与射线BN交于点D,于是只需量出AD,BD的长,就知道AC,BC的长.这个方法可行吗?
根据是什么?你还能设计出其他方案吗?
解:可行.
根据“ASA”可得△ABC≌△ABD,则AC=AD,
BC=BD.
其他方案略.
11.某校七年级学生到野外活动,为测量一池塘两端A,B的距离,甲、乙两名同学分别设计如下两种方案:
甲:如图①,先在平地上取一个可直接到达A,B的点C,再连接AC,BC,并分别延长AC至点D,延长BC至点E,使DC=AC,EC=BC,最后测出DE的长就是A,B的距离.
乙:如图②,过点B作BD⊥AB,在AB的延长线上取一点C,使∠BDC=∠BDA,这时测出BC的长就是A,B的距离.
以上两名同学所设计的方案可行吗?为什么?
解:都可行.理由如下:
两名同学作出的都是全等三角形,甲同学利用的是“边角边”,乙同学利用的是“角边角”,都是根据全等三角形的对应边相等测量的,所以都是可行的.
谢谢欣赏
THANK
YOU
FOR
LISTENING
第四章
三角形
4.5
利用三角形全等测距离
北师大版七年级数学下册
习题课件
4
提示:点击
进入习题
答案显示
6
7
1
2
3
5
SAS;BC
A
B
2.5
m
8
见习题
见习题
D
B
提示:点击
进入习题
答案显示
10
11
9
见习题
见习题
见习题
1.如图,为了测量出A,B两点之间的距离,在地面上找到一点C,连接BC,AC,使∠ACB=90°,然后在BC的延长线上确定点D,使CD=BC,那么只要测量出AD的长度也就得到了A,B两点之间的距离,这样测量的依据是( )
A.AAS
B.SAS
C.ASA
D.SSS
【点拨】因为AC⊥BD,所以∠ACB=∠ACD=90°.在△ACB和△ACD中,AC=AC,∠ACB=∠ACD,CB=CD,所以△ACB≌△ACD(SAS).所以AB=AD(全等三角形的对应边相等).
【答案】B
2.如图,A,B在一水池两侧,若BE=DE,∠B=∠D=90°,CD=10
m,则水池宽AB为( )
A.8
m
B.10
m
C.12
m
D.无法确定
B
3.教室里有几盆花,如图①,要想测量这几盆花两旁的A,B两点间的距离不方便,因此,选点A,B都能到达的一点O,如图②,连接BO并延长BO到点C,使CO=BO,连接AO并延长AO到点D,使DO=AO.那么C,D两点间的距离就是A,B两点间的距离.
SAS
BA
4.如图,将两根钢条AA′,BB′的中点O连在一起,使AA′,BB′可以绕着点O自由转动,就
做成了一个测量工件,由三角形全等得出A′B′的长等于内槽宽AB,那么判定△OAB≌△OA′B′的理由是( )
A.边角边
B.角边角
C.边边边
D.角角边
A
5.如图,某校学生为测量B点到河对面的目标A之间的距离,他们在B点同侧选择了一点C,测得∠ABC=70°,∠ACB=40°,然后在M处立了标杆,使∠CBM=70°,那么他们还应做什么才能测得A,B之间的距离?( )
A.直接测量BM
B.测量BC
C.测量∠A的度数
D.作∠BCN=40°交MB于点N
【点拨】由题意知,∠ABC=∠CBM,BC为公共边,选项D符合“ASA”判定条件.
【答案】D
6.如图,有两个滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,左边滑梯水平方向的长度AB与右边滑梯的高度DE相等,测得BC=2.5
m,则EF= .
【点拨】由题意,因为左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,左边滑梯水平方向的长度AB与右边滑梯的高度DE相等,所以AC=DF,AB=DE.又因为∠BAC=∠EDF,所以△BAC≌△EDF(SAS).所以EF=BC=2.5
m.
【答案】2.5
m
7.如图是由两根钢丝固定的高压电线杆,按要求当两根钢丝与电线杆的夹角相同时,固定效果最好.现已知钢丝触地点到电线杆的距离相等,那么请你判断图中两根钢丝的固定效果是否最好,并说明理由(电线杆的粗细忽略不计).
【点拨】本题易误认为AB=AC,由BO=CO,AO=AO判定△ABO≌△ACO而出错.
8.如图,小刚站在河边的点A处,在河的对面(小刚的正北方向)的点B处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树点C处,接着再向前走了30步到达点D处,然后他左转90°直行,当小刚看到电线塔、树与自己现处的位置E在一条直线上时,
他共走了140步.
(1)根据题意,画出示意图;
解:所画示意图如图所示.
(2)如果小刚一步大约50
cm,估计小刚在点A处时他与电线塔的距离,并说明理由.
9.【2019·南通】如图,有一池塘,要测池塘两端A,B的距离,可先在平地上取一个点C,从点C不经过池塘可以直接到达点A和B.连接AC并延长到点D,使CD=CA.连接BC并延长到点E,使CE=CB.连接DE,那么量出DE的长就是A,B的距离.为什么?
10.如图,某市新开发了一个旅游景点,湖心有一个小岛C,现需要在湖心小岛C上修建一个度假村,因此要测量景点A,B与C的距离.设计人员拟出下列方案:画出∠BAM=∠CAB,∠ABN=∠ABC,射线AM与射线BN交于点D,于是只需量出AD,BD的长,就知道AC,BC的长.这个方法可行吗?
根据是什么?你还能设计出其他方案吗?
解:可行.
根据“ASA”可得△ABC≌△ABD,则AC=AD,
BC=BD.
其他方案略.
11.某校七年级学生到野外活动,为测量一池塘两端A,B的距离,甲、乙两名同学分别设计如下两种方案:
甲:如图①,先在平地上取一个可直接到达A,B的点C,再连接AC,BC,并分别延长AC至点D,延长BC至点E,使DC=AC,EC=BC,最后测出DE的长就是A,B的距离.
乙:如图②,过点B作BD⊥AB,在AB的延长线上取一点C,使∠BDC=∠BDA,这时测出BC的长就是A,B的距离.
以上两名同学所设计的方案可行吗?为什么?
解:都可行.理由如下:
两名同学作出的都是全等三角形,甲同学利用的是“边角边”,乙同学利用的是“角边角”,都是根据全等三角形的对应边相等测量的,所以都是可行的.
谢谢欣赏
THANK
YOU
FOR
LISTENING
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
