1.4用一元二次方程解决问题(2)-苏科版九年级数学上册课件(共17张ppt)
文档属性
| 名称 | 1.4用一元二次方程解决问题(2)-苏科版九年级数学上册课件(共17张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 333.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 00:00:00 | ||
图片预览






文档简介
1.4 用一元二次方程
解决问题(2)
1、学生经历和体验用一元二次方程解决实际问题中有关商品的销售问题的过程,进一步体会一元二次方程也是刻画现实世界数量关系的有效数学模型,增强学生数学的应用意识;
2、进一步提高学生逻辑思维能力,提高学生分析问题、解决问题的能力.
学习目标:
某商品原来每天可销售80件,后来进行价格调整。
(1)市场调查发现,该商品每涨价1元,商场平均每天可少销售2件。
①如果涨价2元,则少卖 件,每天销售量为 件.
②如果涨价3元,则少卖 件,每天销售量为 件.
③如果涨价x元,则少卖 件,每天销售量为 件
4
76
6
74
2x
(80-2x)
自主学习:
某商品原来每天可销售80件,后来进行价格调整。
(2)市场调查发现,该商品每降价3元,商场平均每天可多销售2件。
①如果降价6元,则多卖 件,每天销售量为 件。
②如果降价9元,则多卖 件,每天销售量为 件。
③如果降价x元,则多卖 件,每天销售量为 件。
4
84
6
86
自主学习:
1.某商场销售一批衬衫,平均每天可销售20件.假设在一定的范围内,衬衫的单价每降低1元,商场平均每天可多售出2件,那么,每降低2元,每天可多售出___件;
4
2x
(20+2x)
如果衬衫的单价每降低 x元,每天可多售出_____件,每天销售________ 件.
合作探究:
2.某商场销售一批衬衫,平均每天可销售20件,每件盈利40元.为了扩大销售,增加盈利,商场采取了降价措施.假设在一定的范围内,衬衫的单价每降低1元,商场平均每天多售出2件.如果商场通过销售这批衬衫每天盈利1250元,那么衬衫的单价降了多少元?
分析:设衬衫的单价降了x元,则商场平均每天可多售出____ 件,实际每天销售_______件,每件衬衫盈利 ________元.根据公式“总利润=销售量×单件利润”建立方程.
2x
(20+2x)
(40-x)
合作探究:
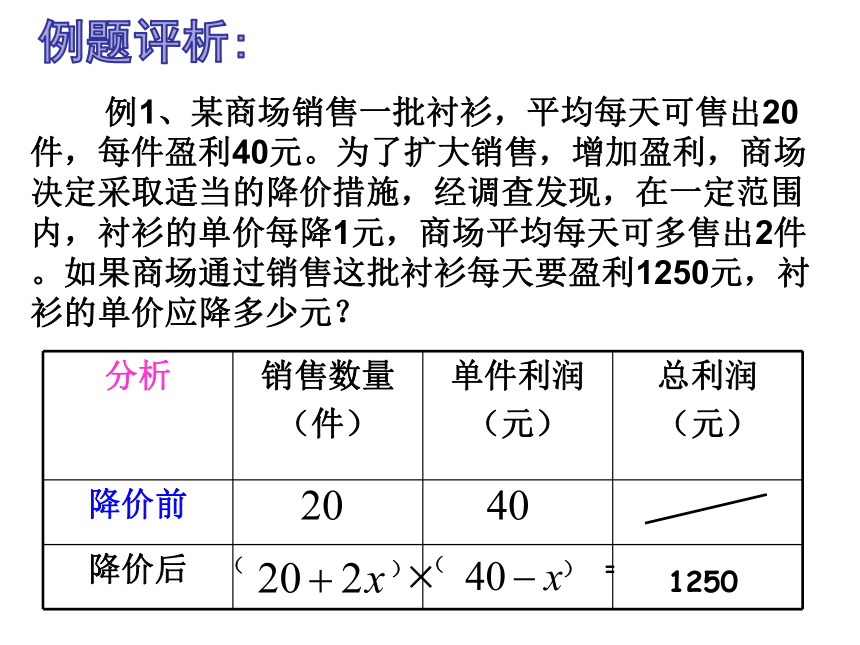
例1、某商场销售一批衬衫,平均每天可售出20件,每件盈利40元。为了扩大销售,增加盈利,商场决定采取适当的降价措施,经调查发现,在一定范围内,衬衫的单价每降1元,商场平均每天可多售出2件。如果商场通过销售这批衬衫每天要盈利1250元,衬衫的单价应降多少元?
分析
销售数量
(件)
单件利润
(元)
总利润
(元)
降价前
降价后
1250
(
)
×
(
)
=
例题评析:
某商店经销一种销售成本为每千克40元的水产品,椐市场分析,若按每千克50元销售,一个月能售出500千克;销售单价每涨1元,月销售量就减少10千克。针对这种水产品的销售情况,要使月销售利润达到8000元,同时又要使顾客得到实惠,销售单价应定为多少?
变式练习:
例2、某商店销售进了一批服装,每件成本50元.如果按每件60元出售,可销售800件;如果每件提价5元出售,其销售量就减少100件.如果商店销售这批服装要获得12000元,那么这种服装售价应定为多少元?该商店应进这种服装多少件?
例题评析:
1、某商店经销一批小家电,每个小家电的成本为40元,经市场调研,售价为50元时,可销售200个;售价每增加1元,销售量将减少10个.如果商店的进货全部销售完,盈利2250元,那么该商店进了多少个这种小家电?售价是多少?
巩固练习:
2.某商店的一种服装,每件成本为50元.
市场调研,售价为60元时,可销售800件;
售价每提高5元,销售量将减少100件.已
知商店销售这批服装获利12000元,问这
种服装每件售价是多少元?(请完成“设”“列”.)
巩固练习:
3.某商店从厂家以每件18元的价格购进一批商品,该商店可以自行定价.据市场调查,该商品的售价与销售量的关系是:若每件售价a元,则可卖出(320-10a)件,但物价部门限定每件商品加价不能超过进货价的25%.如果商店计划要获利400元,则每件商品的售价应定为多少元?需要卖出这种商品多少件?
巩固练习:
某公司组织一批员工到该风景区旅游,支付给旅行社28000元,你能确定参加这次旅游的人数吗?
该公司又组织第二批员工到龙湾风景区旅游,并支付给旅行社29250元,求该公司第二批参加旅游的员工人数。
点拨提升:
小结:
本节课你学到了什么知识?
还有什么疑问?
1.某品牌服装每件进价a元,售价b元,降价x元后则每件利润为_______元.
2.商场销售某品牌服装,每天售出a件。调查发现,该服装每涨价2元,商场平均每天可少销售m件,如果涨价x元则商场平均每天可销售__________ 件.
目标检测:
4.某商店将进价为8元的商品按每件10元售出,每天可售出200件,现在采取提高商品售价减少销售量的办法增加利润,如果这种商品每件的销售价每提高0.5元其销售量就减少10件,问应将每件售价定为多少元时,才能使每天利润为640元?
目标检测:
5.在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?
目标检测:
{5940675A-B579-460E-94D1-54222C63F5DA}销售量y(千克)
…
34.8
32
29.6
28
…
售价x(元/千克)
…
22.6
24
25.2
26
…
解决问题(2)
1、学生经历和体验用一元二次方程解决实际问题中有关商品的销售问题的过程,进一步体会一元二次方程也是刻画现实世界数量关系的有效数学模型,增强学生数学的应用意识;
2、进一步提高学生逻辑思维能力,提高学生分析问题、解决问题的能力.
学习目标:
某商品原来每天可销售80件,后来进行价格调整。
(1)市场调查发现,该商品每涨价1元,商场平均每天可少销售2件。
①如果涨价2元,则少卖 件,每天销售量为 件.
②如果涨价3元,则少卖 件,每天销售量为 件.
③如果涨价x元,则少卖 件,每天销售量为 件
4
76
6
74
2x
(80-2x)
自主学习:
某商品原来每天可销售80件,后来进行价格调整。
(2)市场调查发现,该商品每降价3元,商场平均每天可多销售2件。
①如果降价6元,则多卖 件,每天销售量为 件。
②如果降价9元,则多卖 件,每天销售量为 件。
③如果降价x元,则多卖 件,每天销售量为 件。
4
84
6
86
自主学习:
1.某商场销售一批衬衫,平均每天可销售20件.假设在一定的范围内,衬衫的单价每降低1元,商场平均每天可多售出2件,那么,每降低2元,每天可多售出___件;
4
2x
(20+2x)
如果衬衫的单价每降低 x元,每天可多售出_____件,每天销售________ 件.
合作探究:
2.某商场销售一批衬衫,平均每天可销售20件,每件盈利40元.为了扩大销售,增加盈利,商场采取了降价措施.假设在一定的范围内,衬衫的单价每降低1元,商场平均每天多售出2件.如果商场通过销售这批衬衫每天盈利1250元,那么衬衫的单价降了多少元?
分析:设衬衫的单价降了x元,则商场平均每天可多售出____ 件,实际每天销售_______件,每件衬衫盈利 ________元.根据公式“总利润=销售量×单件利润”建立方程.
2x
(20+2x)
(40-x)
合作探究:
例1、某商场销售一批衬衫,平均每天可售出20件,每件盈利40元。为了扩大销售,增加盈利,商场决定采取适当的降价措施,经调查发现,在一定范围内,衬衫的单价每降1元,商场平均每天可多售出2件。如果商场通过销售这批衬衫每天要盈利1250元,衬衫的单价应降多少元?
分析
销售数量
(件)
单件利润
(元)
总利润
(元)
降价前
降价后
1250
(
)
×
(
)
=
例题评析:
某商店经销一种销售成本为每千克40元的水产品,椐市场分析,若按每千克50元销售,一个月能售出500千克;销售单价每涨1元,月销售量就减少10千克。针对这种水产品的销售情况,要使月销售利润达到8000元,同时又要使顾客得到实惠,销售单价应定为多少?
变式练习:
例2、某商店销售进了一批服装,每件成本50元.如果按每件60元出售,可销售800件;如果每件提价5元出售,其销售量就减少100件.如果商店销售这批服装要获得12000元,那么这种服装售价应定为多少元?该商店应进这种服装多少件?
例题评析:
1、某商店经销一批小家电,每个小家电的成本为40元,经市场调研,售价为50元时,可销售200个;售价每增加1元,销售量将减少10个.如果商店的进货全部销售完,盈利2250元,那么该商店进了多少个这种小家电?售价是多少?
巩固练习:
2.某商店的一种服装,每件成本为50元.
市场调研,售价为60元时,可销售800件;
售价每提高5元,销售量将减少100件.已
知商店销售这批服装获利12000元,问这
种服装每件售价是多少元?(请完成“设”“列”.)
巩固练习:
3.某商店从厂家以每件18元的价格购进一批商品,该商店可以自行定价.据市场调查,该商品的售价与销售量的关系是:若每件售价a元,则可卖出(320-10a)件,但物价部门限定每件商品加价不能超过进货价的25%.如果商店计划要获利400元,则每件商品的售价应定为多少元?需要卖出这种商品多少件?
巩固练习:
某公司组织一批员工到该风景区旅游,支付给旅行社28000元,你能确定参加这次旅游的人数吗?
该公司又组织第二批员工到龙湾风景区旅游,并支付给旅行社29250元,求该公司第二批参加旅游的员工人数。
点拨提升:
小结:
本节课你学到了什么知识?
还有什么疑问?
1.某品牌服装每件进价a元,售价b元,降价x元后则每件利润为_______元.
2.商场销售某品牌服装,每天售出a件。调查发现,该服装每涨价2元,商场平均每天可少销售m件,如果涨价x元则商场平均每天可销售__________ 件.
目标检测:
4.某商店将进价为8元的商品按每件10元售出,每天可售出200件,现在采取提高商品售价减少销售量的办法增加利润,如果这种商品每件的销售价每提高0.5元其销售量就减少10件,问应将每件售价定为多少元时,才能使每天利润为640元?
目标检测:
5.在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?
目标检测:
{5940675A-B579-460E-94D1-54222C63F5DA}销售量y(千克)
…
34.8
32
29.6
28
…
售价x(元/千克)
…
22.6
24
25.2
26
…
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
