北师大版七年级数学下册 第四章 三角形 全章热门考点整合应用 习题课件(共35张ppt)
文档属性
| 名称 | 北师大版七年级数学下册 第四章 三角形 全章热门考点整合应用 习题课件(共35张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 960.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 17:10:49 | ||
图片预览









文档简介
(共35张PPT)
第四章
三角形
全章热门考点整合应用
北师大版七年级数学下册
习题课件
4
提示:点击
进入习题
答案显示
6
7
1
2
3
5
C
见习题
见习题
D
8
见习题
见习题
见习题
见习题
提示:点击
进入习题
答案显示
10
11
12
9
13
见习题
见习题
见习题
见习题
见习题
14
15
见习题
见习题
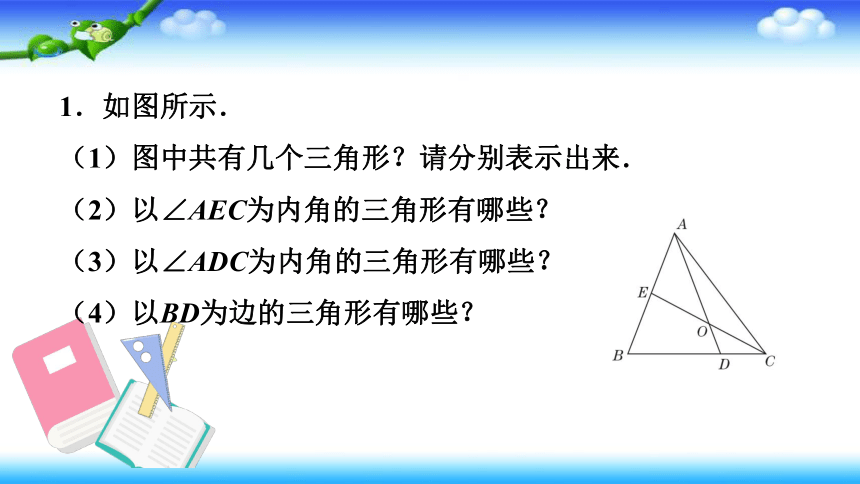
1.如图所示.
(1)图中共有几个三角形?请分别表示出来.
(2)以∠AEC为内角的三角形有哪些?
(3)以∠ADC为内角的三角形有哪些?
(4)以BD为边的三角形有哪些?
(1)图中共有几个三角形?请分别表示出来.
(2)以∠AEC为内角的三角形有哪些?
解:图中共有8个三角形,分别是△ABC,△ABD,△AEO,△AEC,△ADC,△AOC,△ODC,△EBC.
以∠AEC为内角的三角形有△AEO,△AEC.
(3)以∠ADC为内角的三角形有哪些?
(4)以BD为边的三角形有哪些?
解:以∠ADC为内角的三角形有△ADC,△ODC.
以BD为边的三角形只有△ABD.
2.如图,在△ABC中,∠BAC=80°,AD⊥BC于点D,AE平分∠DAC,∠B=60°,求∠DAE的度数.
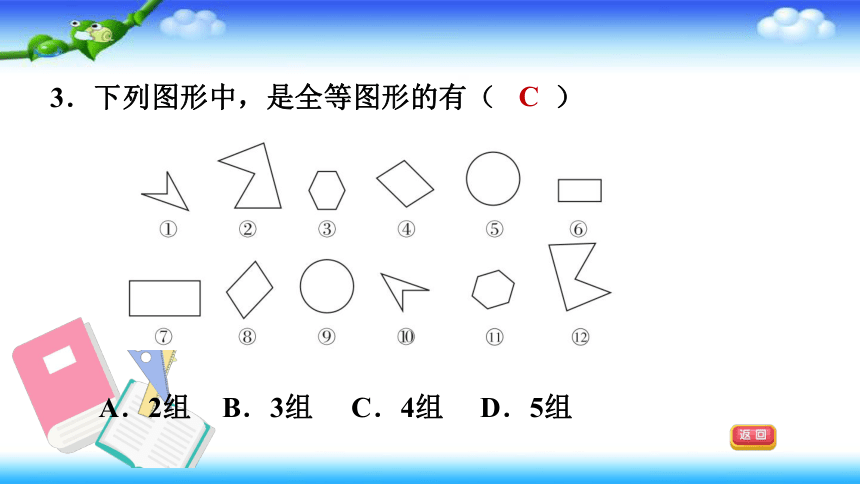
3.下列图形中,是全等图形的有( )
A.2组
B.3组
C.4组
D.5组
C
4.如图,已知△ABE与△ACD全等,∠1=∠2,∠B=∠C.指出全等三角形中的对应边和对应角.
解:AB与AC,AE与AD,BE与CD是对应边;∠B与∠C,∠2与∠1,∠BAE与∠CAD是对应角.
5.A,B,C,D四个工艺品厂的位置如图所示,准备修建一个公共展厅来展销这四个厂的产品,展厅建在何处,才能使四个工艺品厂到公共展厅的距离之和最短,并说明理由.
【点拨】将实际问题转化为数学模型,利用数学知识解决.
6.【2020·宁夏】如图摆放的一副学生用直角三角尺,∠F=30°,∠C=45°,AB与DE相交于点G,当EF∥BC时,∠EGB的度数是( )
A.135°
B.120°
C.115°
D.105°
【点拨】过点G作GH∥BC,则GH∥EF,所以∠HGB=∠B,∠HGE=∠E.又因为△DEF和△ABC都是直角三角形,∠F=30°,∠C=45°,所以∠E=60°,∠B=45°,则由∠EGB=∠HGE+∠HGB即可得出答案.
【答案】D
7.如图,在Rt△ABC中,∠ACB=90°,且AC=BC=4
cm.已知△BCD≌△ACE,求四边形AECD的面积.
【点拨】由△BCD≌△ACE,得S△BCD=S△ACE.从而得到S四边形AECD=S△ACB.
8.如图,已知AB=DC,AD=BC,O是DB的中点,过点O的直线分别交DA和BC的延长线于点E,F.
试说明:∠E=∠F.
9.【2020·黄石】如图,AB=AE,AB∥DE,∠DAB=70°,∠E=40°.
(1)求∠DAE的度数;
解:因为AB∥DE,∠E=40°,
所以∠EAB=∠E=40°.
因为∠DAB=70°,
所以∠DAE=∠DAB-∠EAB=70°-40°=30°.
(2)若∠B=30°,试说明:AD=BC.
10.【2020·内江】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)试说明:AB=CD;
解:因为AB∥CD,所以∠B=∠C.
又因为∠A=∠D,AE=DF,
所以△ABE≌△DCF(AAS).
所以AB=CD.
(2)若AB=CF,∠B=40°,求∠D的度数.
11.【2020·吉林】如图,在△ABC中,AB>AC,点D在边AB上,且BD=CA,过点D作DE∥AC,并截取DE=AB,且点C,E在AB同侧,连接BE.
试说明:△DEB≌△ABC.
解:因为DE∥AC,
所以∠EDB=∠A.
又因为BD=CA,DE=AB,
所以△DEB≌△ABC(SAS).
12.如图,在Rt△ABC中,∠BAC=90°,AB=AC,∠ABC的平分线交AC于点D,过点C作BD的垂线交BD的延长线于点E,交BA的延长线于点F.试说明:
(1)BF=BC;
解:因为BE平分∠ABC,所以∠FBE=∠CBE.
因为CE⊥BE,所以∠FEB=∠CEB=90°.
又因为BE=BE,所以△FBE≌△CBE(ASA).
所以BF=BC.
(2)BD=2CE.
【点拨】解答第(2)小题时,BD与CE不在同一条直线上,也不在同一个三角形中,要说明它们成倍数关系,就要联想到将其中一条线段转化到与另一条线段有关的线段上.
解:因为∠BAC=∠FAC=90°,∠FEB=90°,
所以∠ABD+∠F=∠ACF+∠F=90°.
所以∠ABD=∠ACF.
又因为AB=AC,∠BAD=∠CAF,
所以△BDA≌△CFA(ASA).所以BD=CF.
又因为△FBE≌△CBE,
所以EF=EC,即CF=2EC.所以BD=2CE.
13.如图,AB=DC,∠A=∠D.试说明:∠ABC=∠DCB.
【点拨】说明三角形全等时常需添加适当的辅助线,辅助线的添加以能创造已知条件为上策.如本题取AD,BC的中点就是把中点作为已知条件,这也是几何说明中的一种常用技巧.
解:如图,分别取AD,BC的中点N,M,连接BN,CN,MN,则有AN=ND,BM=MC.
14.如图,在△ABC中,∠BAC=4∠ABC=4∠C,BD⊥AC交CA的延长线于点D,求∠ABD的度数.
【点拨】已知条件中告诉了角的倍分关系时,我们一般用方程求解角的度数较简便.
解:设∠C=x°,则∠ABC=x°,∠BAC=4x°.
在△ABC中,x+x+4x=180,解得x=30.
所以∠BAC=120°.所以∠DAB=60°.
因为BD⊥AC,
所以∠ABD=90°-∠DAB=90°-60°=30°.
15.农科所有一块五边形的试验田如图所示,已知在五边形ABCDE中,∠ABC=∠AED=90°,AB=CD=AE=BC+DE=20
m,求这块试验田的面积.
【点拨】由于五边形试验田是一个不规则的多边形,要求其面积不容易,可以运用转化思想把五边形转化为规则的图形再求面积.
解:如图,延长DE至点F,使EF=BC,连接AC,AD,AF.易得CD=FD.
谢谢欣赏
THANK
YOU
FOR
LISTENING
第四章
三角形
全章热门考点整合应用
北师大版七年级数学下册
习题课件
4
提示:点击
进入习题
答案显示
6
7
1
2
3
5
C
见习题
见习题
D
8
见习题
见习题
见习题
见习题
提示:点击
进入习题
答案显示
10
11
12
9
13
见习题
见习题
见习题
见习题
见习题
14
15
见习题
见习题
1.如图所示.
(1)图中共有几个三角形?请分别表示出来.
(2)以∠AEC为内角的三角形有哪些?
(3)以∠ADC为内角的三角形有哪些?
(4)以BD为边的三角形有哪些?
(1)图中共有几个三角形?请分别表示出来.
(2)以∠AEC为内角的三角形有哪些?
解:图中共有8个三角形,分别是△ABC,△ABD,△AEO,△AEC,△ADC,△AOC,△ODC,△EBC.
以∠AEC为内角的三角形有△AEO,△AEC.
(3)以∠ADC为内角的三角形有哪些?
(4)以BD为边的三角形有哪些?
解:以∠ADC为内角的三角形有△ADC,△ODC.
以BD为边的三角形只有△ABD.
2.如图,在△ABC中,∠BAC=80°,AD⊥BC于点D,AE平分∠DAC,∠B=60°,求∠DAE的度数.
3.下列图形中,是全等图形的有( )
A.2组
B.3组
C.4组
D.5组
C
4.如图,已知△ABE与△ACD全等,∠1=∠2,∠B=∠C.指出全等三角形中的对应边和对应角.
解:AB与AC,AE与AD,BE与CD是对应边;∠B与∠C,∠2与∠1,∠BAE与∠CAD是对应角.
5.A,B,C,D四个工艺品厂的位置如图所示,准备修建一个公共展厅来展销这四个厂的产品,展厅建在何处,才能使四个工艺品厂到公共展厅的距离之和最短,并说明理由.
【点拨】将实际问题转化为数学模型,利用数学知识解决.
6.【2020·宁夏】如图摆放的一副学生用直角三角尺,∠F=30°,∠C=45°,AB与DE相交于点G,当EF∥BC时,∠EGB的度数是( )
A.135°
B.120°
C.115°
D.105°
【点拨】过点G作GH∥BC,则GH∥EF,所以∠HGB=∠B,∠HGE=∠E.又因为△DEF和△ABC都是直角三角形,∠F=30°,∠C=45°,所以∠E=60°,∠B=45°,则由∠EGB=∠HGE+∠HGB即可得出答案.
【答案】D
7.如图,在Rt△ABC中,∠ACB=90°,且AC=BC=4
cm.已知△BCD≌△ACE,求四边形AECD的面积.
【点拨】由△BCD≌△ACE,得S△BCD=S△ACE.从而得到S四边形AECD=S△ACB.
8.如图,已知AB=DC,AD=BC,O是DB的中点,过点O的直线分别交DA和BC的延长线于点E,F.
试说明:∠E=∠F.
9.【2020·黄石】如图,AB=AE,AB∥DE,∠DAB=70°,∠E=40°.
(1)求∠DAE的度数;
解:因为AB∥DE,∠E=40°,
所以∠EAB=∠E=40°.
因为∠DAB=70°,
所以∠DAE=∠DAB-∠EAB=70°-40°=30°.
(2)若∠B=30°,试说明:AD=BC.
10.【2020·内江】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)试说明:AB=CD;
解:因为AB∥CD,所以∠B=∠C.
又因为∠A=∠D,AE=DF,
所以△ABE≌△DCF(AAS).
所以AB=CD.
(2)若AB=CF,∠B=40°,求∠D的度数.
11.【2020·吉林】如图,在△ABC中,AB>AC,点D在边AB上,且BD=CA,过点D作DE∥AC,并截取DE=AB,且点C,E在AB同侧,连接BE.
试说明:△DEB≌△ABC.
解:因为DE∥AC,
所以∠EDB=∠A.
又因为BD=CA,DE=AB,
所以△DEB≌△ABC(SAS).
12.如图,在Rt△ABC中,∠BAC=90°,AB=AC,∠ABC的平分线交AC于点D,过点C作BD的垂线交BD的延长线于点E,交BA的延长线于点F.试说明:
(1)BF=BC;
解:因为BE平分∠ABC,所以∠FBE=∠CBE.
因为CE⊥BE,所以∠FEB=∠CEB=90°.
又因为BE=BE,所以△FBE≌△CBE(ASA).
所以BF=BC.
(2)BD=2CE.
【点拨】解答第(2)小题时,BD与CE不在同一条直线上,也不在同一个三角形中,要说明它们成倍数关系,就要联想到将其中一条线段转化到与另一条线段有关的线段上.
解:因为∠BAC=∠FAC=90°,∠FEB=90°,
所以∠ABD+∠F=∠ACF+∠F=90°.
所以∠ABD=∠ACF.
又因为AB=AC,∠BAD=∠CAF,
所以△BDA≌△CFA(ASA).所以BD=CF.
又因为△FBE≌△CBE,
所以EF=EC,即CF=2EC.所以BD=2CE.
13.如图,AB=DC,∠A=∠D.试说明:∠ABC=∠DCB.
【点拨】说明三角形全等时常需添加适当的辅助线,辅助线的添加以能创造已知条件为上策.如本题取AD,BC的中点就是把中点作为已知条件,这也是几何说明中的一种常用技巧.
解:如图,分别取AD,BC的中点N,M,连接BN,CN,MN,则有AN=ND,BM=MC.
14.如图,在△ABC中,∠BAC=4∠ABC=4∠C,BD⊥AC交CA的延长线于点D,求∠ABD的度数.
【点拨】已知条件中告诉了角的倍分关系时,我们一般用方程求解角的度数较简便.
解:设∠C=x°,则∠ABC=x°,∠BAC=4x°.
在△ABC中,x+x+4x=180,解得x=30.
所以∠BAC=120°.所以∠DAB=60°.
因为BD⊥AC,
所以∠ABD=90°-∠DAB=90°-60°=30°.
15.农科所有一块五边形的试验田如图所示,已知在五边形ABCDE中,∠ABC=∠AED=90°,AB=CD=AE=BC+DE=20
m,求这块试验田的面积.
【点拨】由于五边形试验田是一个不规则的多边形,要求其面积不容易,可以运用转化思想把五边形转化为规则的图形再求面积.
解:如图,延长DE至点F,使EF=BC,连接AC,AD,AF.易得CD=FD.
谢谢欣赏
THANK
YOU
FOR
LISTENING
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
