北师大版七年级数学下册 第四章 三角形4.2图形的全等 习题课件(共28张ppt)
文档属性
| 名称 | 北师大版七年级数学下册 第四章 三角形4.2图形的全等 习题课件(共28张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 663.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 00:00:00 | ||
图片预览






文档简介
(共28张PPT)
第四章
三角形
4.2
图形的全等
北师大版七年级数学下册
习题课件
4
提示:点击
进入习题
答案显示
6
7
1
2
3
5
C
A
见习题
B
8
A
D
C
C
提示:点击
进入习题
答案显示
10
11
9
D
见习题
见习题
12
见习题
13
见习题
14
见习题
1.下列说法中正确的有( )
①用一张底片冲洗出来的10张1寸相片是全等图形;
②我国国旗上的4颗小五角星是全等图形;
③所有的正方形是全等图形;
④全等图形的面积一定相等.
A.1个
B.2个
C.3个
D.4个
C
2.如图,将△ABC沿BC所在的直线平移到△A′B′C′的位置,则△ABC △A′B′C′,图中∠A与____,∠B与_________,∠ACB与_______是对应角.
≌
∠A′
∠A′B′C′
∠C′
3.如图,△AOC≌△BOD,点A与点B、点C与点D分别是对应顶点,下列结论中错误的是( )
A.∠A与∠B是对应角
B.∠AOC与∠BOD是对应角
C.OC与OB是对应边
D.OC与OD是对应边
C
4.如图,点E,F在线段BC上,△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DCE等于( )
A.∠B
B.∠A
C.∠EMF
D.∠AFB
A
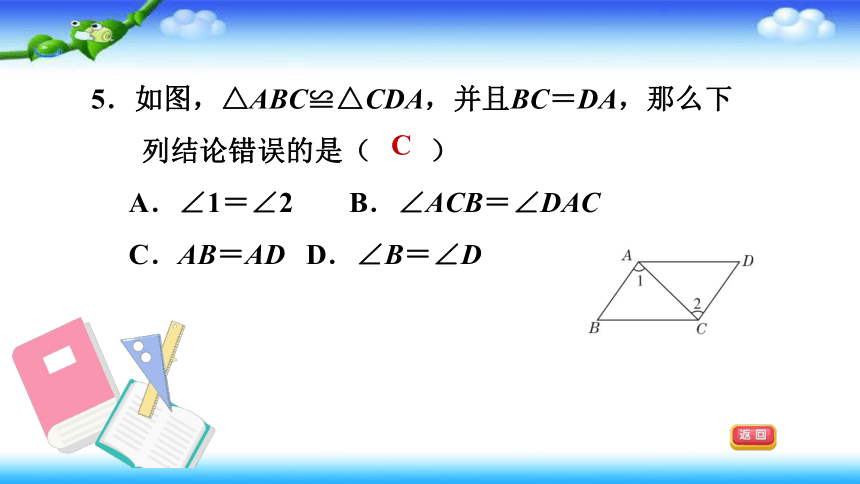
5.如图,△ABC≌△CDA,并且BC=DA,那么下列结论错误的是( )
A.∠1=∠2
B.∠ACB=∠DAC
C.AB=AD
D.∠B=∠D
C
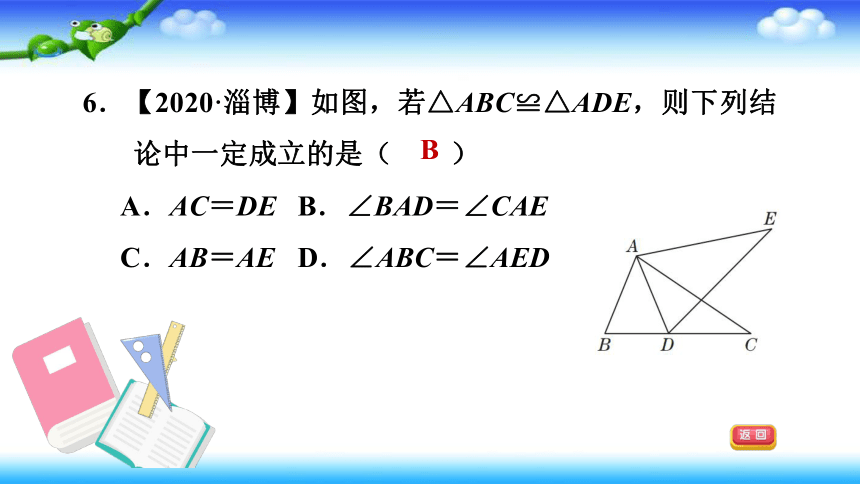
6.【2020·淄博】如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
A.AC=DE
B.∠BAD=∠CAE
C.AB=AE
D.∠ABC=∠AED
B
7.如图,△ABD≌△ACE,若AB=6,AE=4,则CD的长度为( )
A.10
B.6
C.4
D.2
D
8.【中考·吉林】如图,将△ABC折叠,使点A与BC边的中点D重合,折痕为MN,若AB=9,BC=6,则△DNB的周长为( )
A.12
B.13
C.14
D.15
【答案】A
9.【2020·天津】如图,在△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△DEC,使点B的对应点E恰好落在边AC上,点A的对应点为D,延长DE交AB于点F,则下列结论一定正确的是( )
A.AC=DE
B.BC=EF
C.∠AEF=∠D
D.AB⊥DF
【答案】D
10.如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,指出对应边和其他对应角.
错解:AB与AD,AE与AC,BE与CD是对应边;∠BAC与∠DAE是对应角.
诊断:一般情况下,对于图形的全等来说,能够完全重合的部分是相互对应的.实际应用中,应结合图形将对应顶点写在对应位置上,以免出现错误.
正解:AB与AC,AE与AD,BE与CD是对应边;∠E与∠D是对应角.
【点拨】旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.
11.如图,△ABC与△DEC全等,且∠ACB=90°.
(1)说明△ABC经过怎样的变换得到△DEC,并指出对应边和对应角.
(2)直线AB,DE有怎样的位置关系?
解:△ABC与△DEC全等,观察图形发现可将△ABC绕点C顺时针旋转90°得到△DEC.
对应边:AB与DE,AC与DC,BC与EC,
对应角:∠A与∠D,∠ACB与∠DCE,∠ABC与∠DEC.
(1)说明△ABC经过怎样的变换得到△DEC,并指出对应边和对应角.
解:直线AB,DE互相垂直.
(2)直线AB,DE有怎样的位置关系?
12.如图,已知点B,D,E,C在同一条直线上,△ABE≌△ACD.
(1)说明△ABE经过怎样的变化后可与△ACD重合.
解:过点A作DE的垂线,作△ABE
关于此线的轴对称图形,即可得
到△ACD.
(2)∠BAD与∠CAE有何关系?请说明理由.
解:∠BAD=∠CAE.理由如下:
因为△ABE≌△ACD,
所以∠BAE=∠CAD.
所以∠BAE-∠DAE=∠CAD-∠DAE,
即∠BAD=∠CAE.
(3)BD与CE相等吗?为什么?
解:BD与CE相等.理由如下:
因为△ABE≌△ACD,所以BE=CD.
所以BE-DE=CD-DE,即BD=CE.
13.如图,点E,D分别是等边△ABC的边CB,AC延长线上的点,连接AE,DB,延长DB交AE于点F.已知△ABE≌△BCD.
(1)写出所有与∠BAE相等的角,并说明理由;
解:与∠BAE相等的角有∠CBD,∠EBF.理由如下:
因为△ABE≌△BCD,
所以∠BAE=∠CBD.
因为∠CBD=∠EBF,
所以∠BAE=∠EBF.
(2)求∠AFB的度数.
解:因为△ABE≌△BCD,所以∠E=∠D.
因为180°-∠AFB=∠EFB=180°-∠E-∠EBF,
所以∠AFB=∠E+∠EBF,同理,∠ACB=∠D+∠CBD.又因为∠EBF=∠CBD,所以∠AFB=∠ACB.
因为△ABC为等边三角形,所以∠ACB=60°.
所以∠AFB=60°.
14.如图,A,D,E三点在同一条直线上,且△BAD≌△ACE.
(1)试说明:BD=DE+CE.
解:因为△BAD≌△ACE,
所以BD=AE,AD=CE.
又因为A,D,E三点在同一条直线上,
所以AE=DE+AD.所以BD=DE+CE.
(2)问:△ABD满足什么条件时,BD∥CE?
解:△ABD满足∠ADB=90°时,BD∥CE.
因为∠ADB=90°,所以∠BDE=90°.
又因为△BAD≌△ACE,所以∠CEA=∠ADB=90°.
所以∠CEA=∠BDE.所以BD∥CE.
谢谢欣赏
THANK
YOU
FOR
LISTENING
第四章
三角形
4.2
图形的全等
北师大版七年级数学下册
习题课件
4
提示:点击
进入习题
答案显示
6
7
1
2
3
5
C
A
见习题
B
8
A
D
C
C
提示:点击
进入习题
答案显示
10
11
9
D
见习题
见习题
12
见习题
13
见习题
14
见习题
1.下列说法中正确的有( )
①用一张底片冲洗出来的10张1寸相片是全等图形;
②我国国旗上的4颗小五角星是全等图形;
③所有的正方形是全等图形;
④全等图形的面积一定相等.
A.1个
B.2个
C.3个
D.4个
C
2.如图,将△ABC沿BC所在的直线平移到△A′B′C′的位置,则△ABC △A′B′C′,图中∠A与____,∠B与_________,∠ACB与_______是对应角.
≌
∠A′
∠A′B′C′
∠C′
3.如图,△AOC≌△BOD,点A与点B、点C与点D分别是对应顶点,下列结论中错误的是( )
A.∠A与∠B是对应角
B.∠AOC与∠BOD是对应角
C.OC与OB是对应边
D.OC与OD是对应边
C
4.如图,点E,F在线段BC上,△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DCE等于( )
A.∠B
B.∠A
C.∠EMF
D.∠AFB
A
5.如图,△ABC≌△CDA,并且BC=DA,那么下列结论错误的是( )
A.∠1=∠2
B.∠ACB=∠DAC
C.AB=AD
D.∠B=∠D
C
6.【2020·淄博】如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
A.AC=DE
B.∠BAD=∠CAE
C.AB=AE
D.∠ABC=∠AED
B
7.如图,△ABD≌△ACE,若AB=6,AE=4,则CD的长度为( )
A.10
B.6
C.4
D.2
D
8.【中考·吉林】如图,将△ABC折叠,使点A与BC边的中点D重合,折痕为MN,若AB=9,BC=6,则△DNB的周长为( )
A.12
B.13
C.14
D.15
【答案】A
9.【2020·天津】如图,在△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△DEC,使点B的对应点E恰好落在边AC上,点A的对应点为D,延长DE交AB于点F,则下列结论一定正确的是( )
A.AC=DE
B.BC=EF
C.∠AEF=∠D
D.AB⊥DF
【答案】D
10.如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,指出对应边和其他对应角.
错解:AB与AD,AE与AC,BE与CD是对应边;∠BAC与∠DAE是对应角.
诊断:一般情况下,对于图形的全等来说,能够完全重合的部分是相互对应的.实际应用中,应结合图形将对应顶点写在对应位置上,以免出现错误.
正解:AB与AC,AE与AD,BE与CD是对应边;∠E与∠D是对应角.
【点拨】旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.
11.如图,△ABC与△DEC全等,且∠ACB=90°.
(1)说明△ABC经过怎样的变换得到△DEC,并指出对应边和对应角.
(2)直线AB,DE有怎样的位置关系?
解:△ABC与△DEC全等,观察图形发现可将△ABC绕点C顺时针旋转90°得到△DEC.
对应边:AB与DE,AC与DC,BC与EC,
对应角:∠A与∠D,∠ACB与∠DCE,∠ABC与∠DEC.
(1)说明△ABC经过怎样的变换得到△DEC,并指出对应边和对应角.
解:直线AB,DE互相垂直.
(2)直线AB,DE有怎样的位置关系?
12.如图,已知点B,D,E,C在同一条直线上,△ABE≌△ACD.
(1)说明△ABE经过怎样的变化后可与△ACD重合.
解:过点A作DE的垂线,作△ABE
关于此线的轴对称图形,即可得
到△ACD.
(2)∠BAD与∠CAE有何关系?请说明理由.
解:∠BAD=∠CAE.理由如下:
因为△ABE≌△ACD,
所以∠BAE=∠CAD.
所以∠BAE-∠DAE=∠CAD-∠DAE,
即∠BAD=∠CAE.
(3)BD与CE相等吗?为什么?
解:BD与CE相等.理由如下:
因为△ABE≌△ACD,所以BE=CD.
所以BE-DE=CD-DE,即BD=CE.
13.如图,点E,D分别是等边△ABC的边CB,AC延长线上的点,连接AE,DB,延长DB交AE于点F.已知△ABE≌△BCD.
(1)写出所有与∠BAE相等的角,并说明理由;
解:与∠BAE相等的角有∠CBD,∠EBF.理由如下:
因为△ABE≌△BCD,
所以∠BAE=∠CBD.
因为∠CBD=∠EBF,
所以∠BAE=∠EBF.
(2)求∠AFB的度数.
解:因为△ABE≌△BCD,所以∠E=∠D.
因为180°-∠AFB=∠EFB=180°-∠E-∠EBF,
所以∠AFB=∠E+∠EBF,同理,∠ACB=∠D+∠CBD.又因为∠EBF=∠CBD,所以∠AFB=∠ACB.
因为△ABC为等边三角形,所以∠ACB=60°.
所以∠AFB=60°.
14.如图,A,D,E三点在同一条直线上,且△BAD≌△ACE.
(1)试说明:BD=DE+CE.
解:因为△BAD≌△ACE,
所以BD=AE,AD=CE.
又因为A,D,E三点在同一条直线上,
所以AE=DE+AD.所以BD=DE+CE.
(2)问:△ABD满足什么条件时,BD∥CE?
解:△ABD满足∠ADB=90°时,BD∥CE.
因为∠ADB=90°,所以∠BDE=90°.
又因为△BAD≌△ACE,所以∠CEA=∠ADB=90°.
所以∠CEA=∠BDE.所以BD∥CE.
谢谢欣赏
THANK
YOU
FOR
LISTENING
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
