北师大版九年级数学下册 3.1 圆 课件(18张)
文档属性
| 名称 | 北师大版九年级数学下册 3.1 圆 课件(18张) |  | |
| 格式 | pptx | ||
| 文件大小 | 707.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 17:09:46 | ||
图片预览


文档简介
第1课 圆
{5940675A-B579-460E-94D1-54222C63F5DA}
定义
图例
表示方法
注意
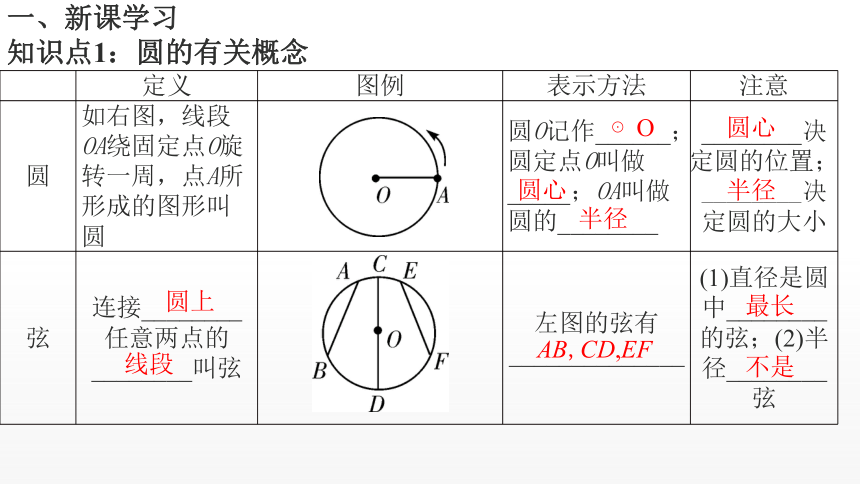
圆
如右图,线段OA绕固定点O旋转一周,点A所形成的图形叫圆
圆O记作______; 圆定点O叫做_____;OA叫做圆的________
________决定圆的位置;________决定圆的大小
弦
连接________任意两点的________叫弦
左图的弦有______________
(1)直径是圆中________的弦;(2)半径________弦
一、新课学习
知识点1:圆的有关概念
圆上
线段
圆心
半径
最长
不是
AB,CD,EF
⊙O
圆心
半径
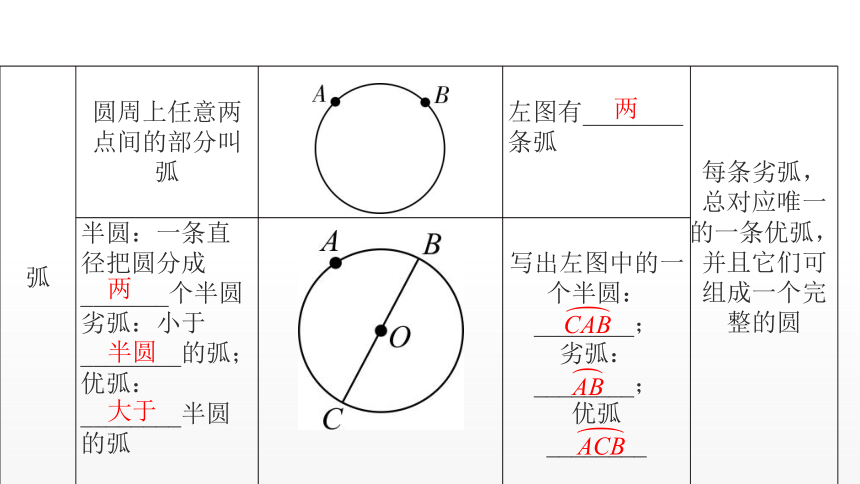
{5940675A-B579-460E-94D1-54222C63F5DA}弧
圆周上任意两点间的部分叫弧
左图有________条弧
每条劣弧,总对应唯一的一条优弧,并且它们可组成一个完整的圆
半圆:一条直径把圆分成_______个半圆
劣弧:小于________的弧;优弧:________半圆的弧
写出左图中的一个半圆:________;
劣弧:
________;
优弧
________
两
两
半圆
大于
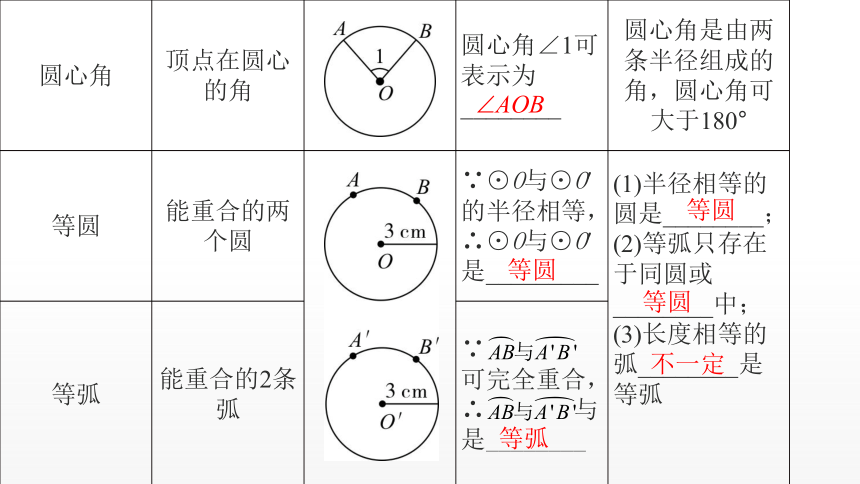
{5940675A-B579-460E-94D1-54222C63F5DA}圆心角
顶点在圆心的角
圆心角∠1可表示为________
圆心角是由两条半径组成的角,圆心角可大于180°
等圆
能重合的两个圆
∵⊙O与⊙O′的半径相等,∴⊙O与⊙O′是_________
(1)半径相等的圆是________;(2)等弧只存在于同圆或________中;
(3)长度相等的弧________是等弧
等弧
能重合的2条弧
∵ 可完全重合,∴ 与是________
等圆
等圆
等圆
不一定
等弧
1.(例1)如图,在⊙O中,
(1)半径有:________________;
(2)直径有:________________;
(3)弦有:________________;
(4)劣弧 对应的优弧是_______
劣弧________对应的优弧是________;
(5)半圆弧有:________________.
OA ,
OB
AB
AC,
BC,
AB
提示:在直径AB上方圆周上标一点E
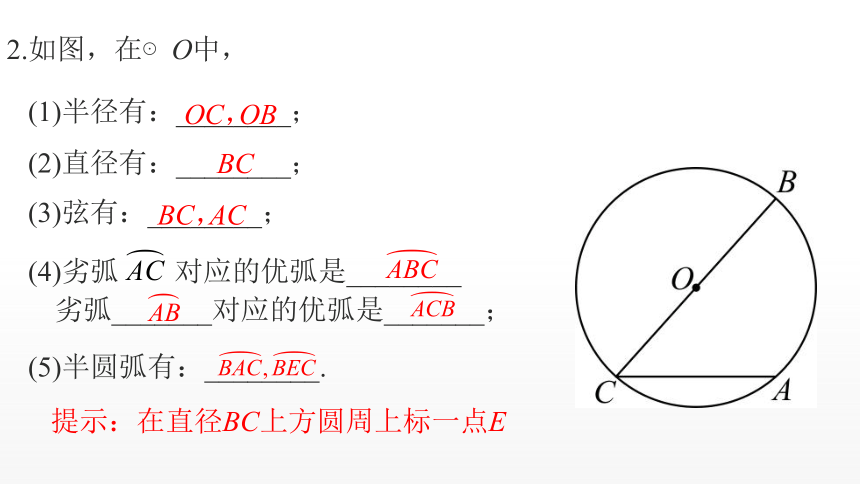
2.如图,在⊙O中,
(1)半径有:________;
(2)直径有:________;
(3)弦有:________;
(4)劣弧 对应的优弧是________
劣弧_______对应的优弧是_______;
(5)半圆弧有:________.
OC,
OB
BC
BC,
AC
提示:在直径BC上方圆周上标一点E
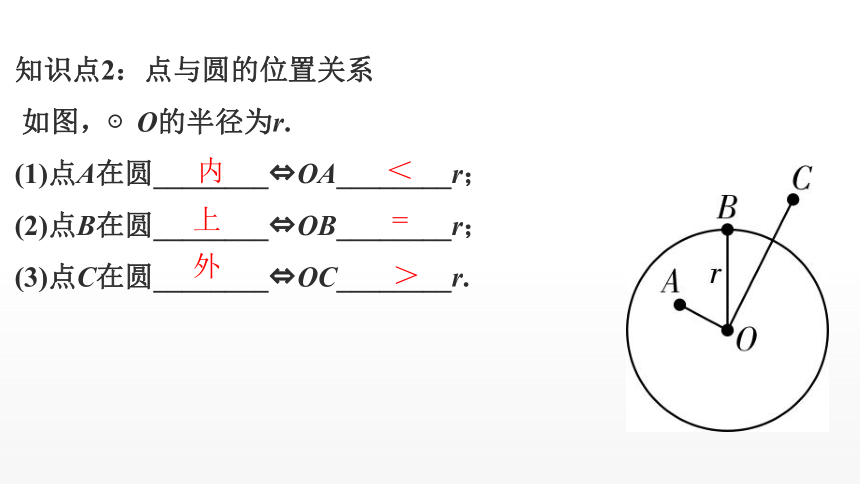
知识点2:点与圆的位置关系
如图,⊙O的半径为r.
(1)点A在圆________?OA________r;
(2)点B在圆________?OB________r;
(3)点C在圆________?OC________r.
内
<
上
=
外
>
3.如图,在⊙O中,下列判断正确的是( )
A.点A在圆上
B.点B在圆上
C.点C在圆上
D.点O在圆上
B
4.(例2)已知⊙O的半径r=5 cm.
(1)若OP=5 cm,则点P在圆________;
(2)若OP=4 cm,则点P在________;
(3)若点P到圆心O的距离为6 cm,则点P在________.
上
圆内
圆外
5.已知⊙O的半径为r,点P到圆心距离d=5.
(1)若r=4,则点P在________;
(2)若r=________,则点P在圆上;
(3)若________,则点P在圆外.
圆外
5
0<r<5
6.若⊙O的圆心坐标为(0,0),半径为5,点A的坐标为(3,4),
则点A在⊙O________.
上
7.若⊙O的半径为4,圆心O的坐标为(0,0),则点P(0,-5)
在⊙O________.
外
二、过关检测
第1关
8.如图,在⊙O中,已知∠A=30°.
(1)图中的弦有:________,
劣弧有:________;
(2)∠AOB=________.
AB
120°
9.如图,在⊙O中,AC是直径,若∠AOB=60°,
则∠C=________,∠A=________.
30°
60°
第2关
10.如图,OA,OB是圆的两条半径,∠AOB=90°,AO=4,
则∠A=________,AB的长=________.
45°
11.如图,⊙O的弦AB与半径OC的延长线交于点D,BD=OA,
若∠AOD=120°,则∠D=________.
20°
第3关
12.如图,AB,CD为⊙O的两条直径,M,N分别为AO,BO
的中点.求证:四边形CMDN为平行四边形.
证明:在⊙O中,OA=OB=OC=OD
∵M,N分别为OA,BO的中点
∴OM= OA,ON= OB
∴OM=ON
∴四边形CMDN为平行四边形
13.如图,AB,CD为⊙O的两条直径,求证:四边形
ACBD为矩形.
证明:∵AB,CD为⊙O的直径
∴OA=OB=OC=OD
∴四边形ACBD为平行四边形
∵AB=CD
∴ ACBD为矩形
{5940675A-B579-460E-94D1-54222C63F5DA}
定义
图例
表示方法
注意
圆
如右图,线段OA绕固定点O旋转一周,点A所形成的图形叫圆
圆O记作______; 圆定点O叫做_____;OA叫做圆的________
________决定圆的位置;________决定圆的大小
弦
连接________任意两点的________叫弦
左图的弦有______________
(1)直径是圆中________的弦;(2)半径________弦
一、新课学习
知识点1:圆的有关概念
圆上
线段
圆心
半径
最长
不是
AB,CD,EF
⊙O
圆心
半径
{5940675A-B579-460E-94D1-54222C63F5DA}弧
圆周上任意两点间的部分叫弧
左图有________条弧
每条劣弧,总对应唯一的一条优弧,并且它们可组成一个完整的圆
半圆:一条直径把圆分成_______个半圆
劣弧:小于________的弧;优弧:________半圆的弧
写出左图中的一个半圆:________;
劣弧:
________;
优弧
________
两
两
半圆
大于
{5940675A-B579-460E-94D1-54222C63F5DA}圆心角
顶点在圆心的角
圆心角∠1可表示为________
圆心角是由两条半径组成的角,圆心角可大于180°
等圆
能重合的两个圆
∵⊙O与⊙O′的半径相等,∴⊙O与⊙O′是_________
(1)半径相等的圆是________;(2)等弧只存在于同圆或________中;
(3)长度相等的弧________是等弧
等弧
能重合的2条弧
∵ 可完全重合,∴ 与是________
等圆
等圆
等圆
不一定
等弧
1.(例1)如图,在⊙O中,
(1)半径有:________________;
(2)直径有:________________;
(3)弦有:________________;
(4)劣弧 对应的优弧是_______
劣弧________对应的优弧是________;
(5)半圆弧有:________________.
OA ,
OB
AB
AC,
BC,
AB
提示:在直径AB上方圆周上标一点E
2.如图,在⊙O中,
(1)半径有:________;
(2)直径有:________;
(3)弦有:________;
(4)劣弧 对应的优弧是________
劣弧_______对应的优弧是_______;
(5)半圆弧有:________.
OC,
OB
BC
BC,
AC
提示:在直径BC上方圆周上标一点E
知识点2:点与圆的位置关系
如图,⊙O的半径为r.
(1)点A在圆________?OA________r;
(2)点B在圆________?OB________r;
(3)点C在圆________?OC________r.
内
<
上
=
外
>
3.如图,在⊙O中,下列判断正确的是( )
A.点A在圆上
B.点B在圆上
C.点C在圆上
D.点O在圆上
B
4.(例2)已知⊙O的半径r=5 cm.
(1)若OP=5 cm,则点P在圆________;
(2)若OP=4 cm,则点P在________;
(3)若点P到圆心O的距离为6 cm,则点P在________.
上
圆内
圆外
5.已知⊙O的半径为r,点P到圆心距离d=5.
(1)若r=4,则点P在________;
(2)若r=________,则点P在圆上;
(3)若________,则点P在圆外.
圆外
5
0<r<5
6.若⊙O的圆心坐标为(0,0),半径为5,点A的坐标为(3,4),
则点A在⊙O________.
上
7.若⊙O的半径为4,圆心O的坐标为(0,0),则点P(0,-5)
在⊙O________.
外
二、过关检测
第1关
8.如图,在⊙O中,已知∠A=30°.
(1)图中的弦有:________,
劣弧有:________;
(2)∠AOB=________.
AB
120°
9.如图,在⊙O中,AC是直径,若∠AOB=60°,
则∠C=________,∠A=________.
30°
60°
第2关
10.如图,OA,OB是圆的两条半径,∠AOB=90°,AO=4,
则∠A=________,AB的长=________.
45°
11.如图,⊙O的弦AB与半径OC的延长线交于点D,BD=OA,
若∠AOD=120°,则∠D=________.
20°
第3关
12.如图,AB,CD为⊙O的两条直径,M,N分别为AO,BO
的中点.求证:四边形CMDN为平行四边形.
证明:在⊙O中,OA=OB=OC=OD
∵M,N分别为OA,BO的中点
∴OM= OA,ON= OB
∴OM=ON
∴四边形CMDN为平行四边形
13.如图,AB,CD为⊙O的两条直径,求证:四边形
ACBD为矩形.
证明:∵AB,CD为⊙O的直径
∴OA=OB=OC=OD
∴四边形ACBD为平行四边形
∵AB=CD
∴ ACBD为矩形
