北师大版七年级数学下册 第四章 三角形4.3.1用“ 边边边”判定三角形全等 习题课件(共22张ppt)
文档属性
| 名称 | 北师大版七年级数学下册 第四章 三角形4.3.1用“ 边边边”判定三角形全等 习题课件(共22张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 832.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 00:00:00 | ||
图片预览




文档简介
(共22张PPT)
第四章
三角形
4.3
探索三角形全等的条件
第1课时
用“
边边边”判定三角形全等
北师大版七年级数学下册
习题课件
4
提示:点击
进入习题
答案显示
6
7
1
2
3
5
A
D
B
B
8
见习题
C
C
C
提示:点击
进入习题
答案显示
10
11
9
见习题
见习题
见习题
12
见习题
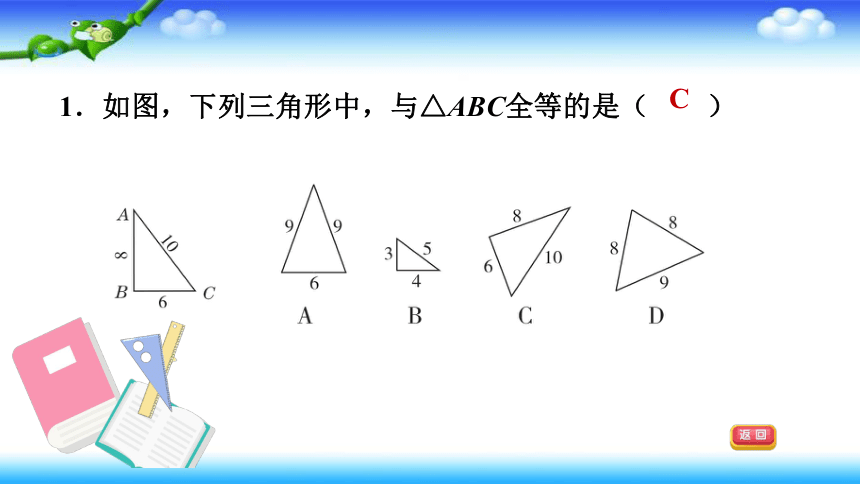
1.如图,下列三角形中,与△ABC全等的是( )
C
2.如图,已知AB=AC,AE=AD,点B,D,E,C在同一条直线上,要利用“SSS”推理得出△ABE≌△ACD,还需要添加的一个条件可以是( )
A.BD=DE
B.BD=CE
C.DE=CE
D.以上都不对
B
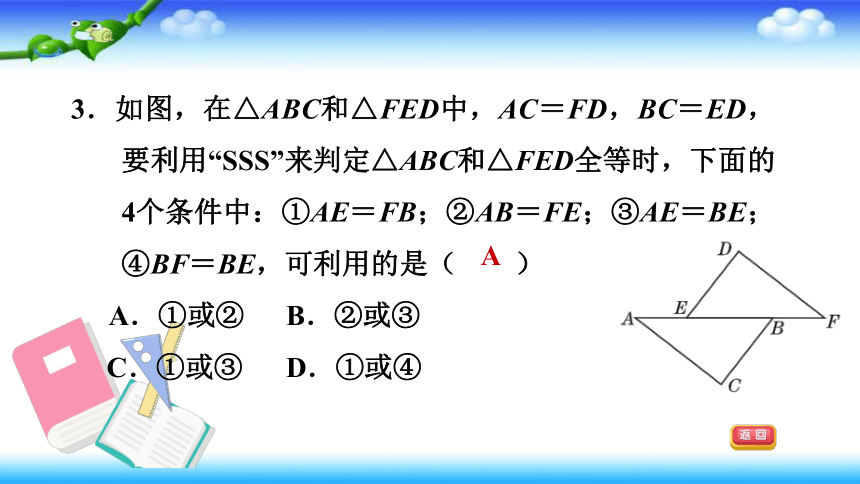
3.如图,在△ABC和△FED中,AC=FD,BC=ED,要利用“SSS”来判定△ABC和△FED全等时,下面的4个条件中:①AE=FB;②AB=FE;③AE=BE;④BF=BE,可利用的是( )
A.①或②
B.②或③
C.①或③
D.①或④
A
4.如图,已知AE=AD,AB=AC,EC=DB,下列结论:
①∠C=∠B;②∠D=∠E;③∠EAD=∠BAC;④∠B=∠E.其中错误的是( )
A.①②
B.②③
C.③④
D.只有④
D
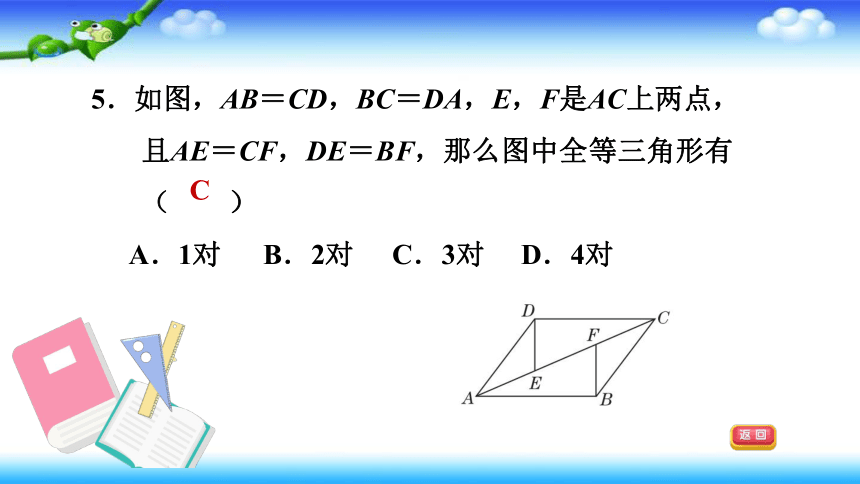
5.如图,AB=CD,BC=DA,E,F是AC上两点,且AE=CF,DE=BF,那么图中全等三角形有( )
A.1对
B.2对
C.3对
D.4对
C
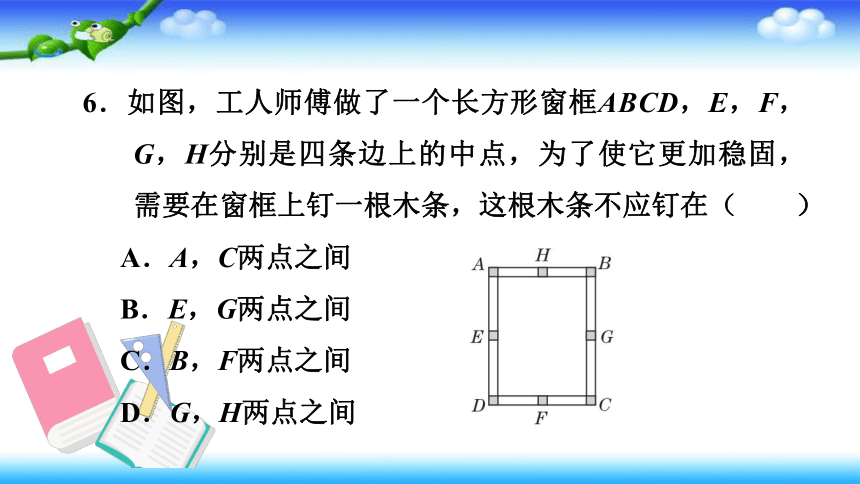
6.如图,工人师傅做了一个长方形窗框ABCD,E,F,G,H分别是四条边上的中点,为了使它更加稳固,需要在窗框上钉一根木条,这根木条不应钉在( )
A.A,C两点之间
B.E,G两点之间
C.B,F两点之间
D.G,H两点之间
【点拨】选项A,C,D中都构成了三角形,增加了稳定性;选项B中,木条钉在E,G两点之间,没有构成三角形.故选B.
【答案】B
7.在实际生活中,我们经常利用几何图形的稳定性或不稳定性的性质,下列实物图中利用了稳定性的是( )
C
8.如图,AB=AC,DB=DC,EB=EC.图中共有几对全等三角形?请一一写出来.
【点拨】本题应根据已知条件去判定全等三角形,在找全等三角形时,容易考虑不全面导致漏解.
解:题图中共有3对全等三角形,分别是△ABD≌△ACD,△ABE≌△ACE,△DBE≌△DCE.
9.如图,已知点B,E,C,F在同一条直线上,AB=DE,AC=DF,BE=CF.试说明:
(1)△ABC≌△DEF;
(2)AB∥DE.
解:由(1)得△ABC≌△DEF,
所以∠B=∠DEF.
所以AB∥DE.
10.【2020·云南】如图,已知AD=BC,BD=AC.
试说明:∠ADB=∠BCA.
解:因为AD=BC,BD=AC,AB=BA,
所以△ADB≌△BCA(SSS).
所以∠ADB=∠BCA.
【点拨】本题运用了构造法,通过连接OE,构造△OAE,△OCE,将欲说明相等的∠A,∠C分别置于这两个三角形中,然后通过说明这两个三角形全等可得∠A=∠C.
11.如图,已知线段AB,CD相交于点O,AD,CB的延长线交于点E,OA=OC,EA=EC.
(1)试说明:∠A=∠C;
(2)在(1)的解答过程中,需要作辅助线,
它的意图是什么?
解:如图,连接OE.
11.如图,已知线段AB,CD相交于点O,AD,CB的延长线交于点E,OA=OC,EA=EC.
(1)试说明:∠A=∠C;
解:构造全等三角形.
(2)在(1)的解答过程中,需要作辅助线,它的意图是什么?
12.如图,在△ABC中,AC=BC,D是AB上的一点,AE⊥CD于点E,BF⊥CD于点F.若CE=BF,AE=EF+BF,试判断AC与BC的位置关系,并说明理由.
解:AC⊥BC.
理由如下:因为CE=BF,AE=EF+BF,
CF=CE+EF,所以AE=CF.
谢谢欣赏
THANK
YOU
FOR
LISTENING
第四章
三角形
4.3
探索三角形全等的条件
第1课时
用“
边边边”判定三角形全等
北师大版七年级数学下册
习题课件
4
提示:点击
进入习题
答案显示
6
7
1
2
3
5
A
D
B
B
8
见习题
C
C
C
提示:点击
进入习题
答案显示
10
11
9
见习题
见习题
见习题
12
见习题
1.如图,下列三角形中,与△ABC全等的是( )
C
2.如图,已知AB=AC,AE=AD,点B,D,E,C在同一条直线上,要利用“SSS”推理得出△ABE≌△ACD,还需要添加的一个条件可以是( )
A.BD=DE
B.BD=CE
C.DE=CE
D.以上都不对
B
3.如图,在△ABC和△FED中,AC=FD,BC=ED,要利用“SSS”来判定△ABC和△FED全等时,下面的4个条件中:①AE=FB;②AB=FE;③AE=BE;④BF=BE,可利用的是( )
A.①或②
B.②或③
C.①或③
D.①或④
A
4.如图,已知AE=AD,AB=AC,EC=DB,下列结论:
①∠C=∠B;②∠D=∠E;③∠EAD=∠BAC;④∠B=∠E.其中错误的是( )
A.①②
B.②③
C.③④
D.只有④
D
5.如图,AB=CD,BC=DA,E,F是AC上两点,且AE=CF,DE=BF,那么图中全等三角形有( )
A.1对
B.2对
C.3对
D.4对
C
6.如图,工人师傅做了一个长方形窗框ABCD,E,F,G,H分别是四条边上的中点,为了使它更加稳固,需要在窗框上钉一根木条,这根木条不应钉在( )
A.A,C两点之间
B.E,G两点之间
C.B,F两点之间
D.G,H两点之间
【点拨】选项A,C,D中都构成了三角形,增加了稳定性;选项B中,木条钉在E,G两点之间,没有构成三角形.故选B.
【答案】B
7.在实际生活中,我们经常利用几何图形的稳定性或不稳定性的性质,下列实物图中利用了稳定性的是( )
C
8.如图,AB=AC,DB=DC,EB=EC.图中共有几对全等三角形?请一一写出来.
【点拨】本题应根据已知条件去判定全等三角形,在找全等三角形时,容易考虑不全面导致漏解.
解:题图中共有3对全等三角形,分别是△ABD≌△ACD,△ABE≌△ACE,△DBE≌△DCE.
9.如图,已知点B,E,C,F在同一条直线上,AB=DE,AC=DF,BE=CF.试说明:
(1)△ABC≌△DEF;
(2)AB∥DE.
解:由(1)得△ABC≌△DEF,
所以∠B=∠DEF.
所以AB∥DE.
10.【2020·云南】如图,已知AD=BC,BD=AC.
试说明:∠ADB=∠BCA.
解:因为AD=BC,BD=AC,AB=BA,
所以△ADB≌△BCA(SSS).
所以∠ADB=∠BCA.
【点拨】本题运用了构造法,通过连接OE,构造△OAE,△OCE,将欲说明相等的∠A,∠C分别置于这两个三角形中,然后通过说明这两个三角形全等可得∠A=∠C.
11.如图,已知线段AB,CD相交于点O,AD,CB的延长线交于点E,OA=OC,EA=EC.
(1)试说明:∠A=∠C;
(2)在(1)的解答过程中,需要作辅助线,
它的意图是什么?
解:如图,连接OE.
11.如图,已知线段AB,CD相交于点O,AD,CB的延长线交于点E,OA=OC,EA=EC.
(1)试说明:∠A=∠C;
解:构造全等三角形.
(2)在(1)的解答过程中,需要作辅助线,它的意图是什么?
12.如图,在△ABC中,AC=BC,D是AB上的一点,AE⊥CD于点E,BF⊥CD于点F.若CE=BF,AE=EF+BF,试判断AC与BC的位置关系,并说明理由.
解:AC⊥BC.
理由如下:因为CE=BF,AE=EF+BF,
CF=CE+EF,所以AE=CF.
谢谢欣赏
THANK
YOU
FOR
LISTENING
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
