北师大版七年级数学下册 第四章 三角形4.3.3用“ 边角边”判定三角形全等 习题课件(共27张ppt)
文档属性
| 名称 | 北师大版七年级数学下册 第四章 三角形4.3.3用“ 边角边”判定三角形全等 习题课件(共27张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 703.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 00:00:00 | ||
图片预览



文档简介
(共27张PPT)
第四章
三角形
4.3
探索三角形全等的条件
第3课时
用“
边角边”判定三角形全等
北师大版七年级数学下册
习题课件
4
提示:点击
进入习题
答案显示
6
7
1
2
3
5
B
C
A
82°
8
见习题
见习题
B
B
提示:点击
进入习题
答案显示
10
11
9
见习题
见习题
见习题
12
见习题
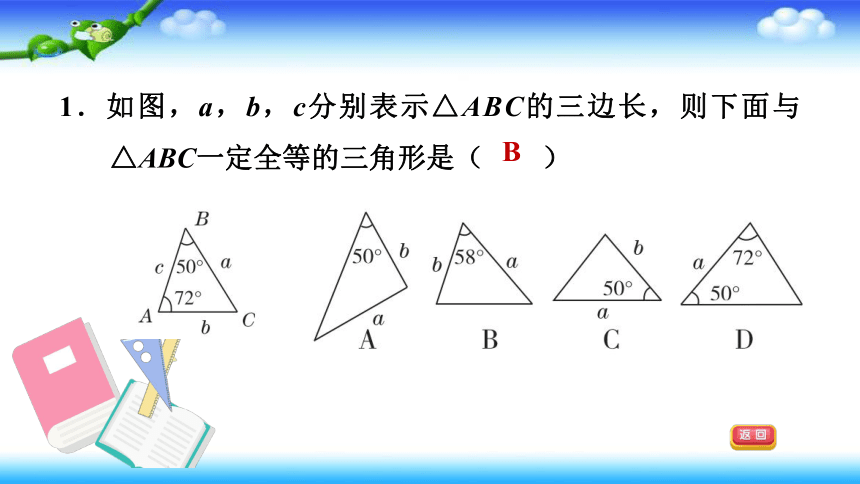
1.如图,a,b,c分别表示△ABC的三边长,则下面与△ABC一定全等的三角形是( )
B
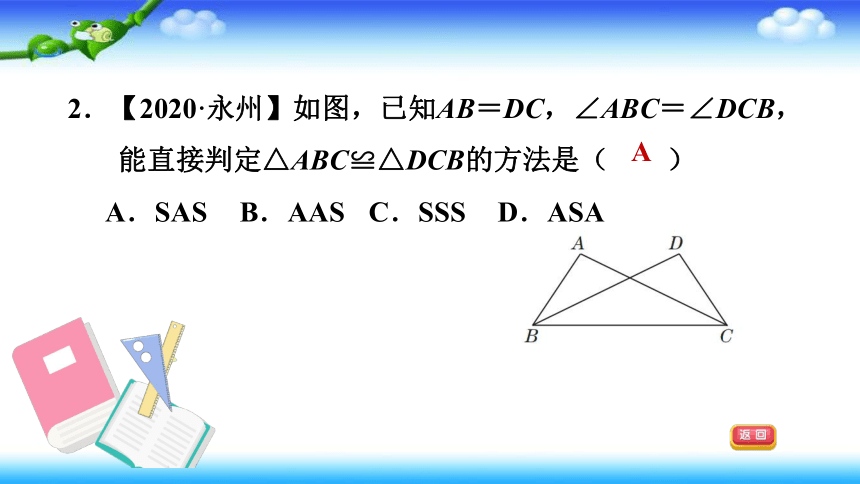
2.【2020·永州】如图,已知AB=DC,∠ABC=∠DCB,能直接判定△ABC≌△DCB的方法是( )
A.SAS
B.AAS
C.SSS
D.ASA
A
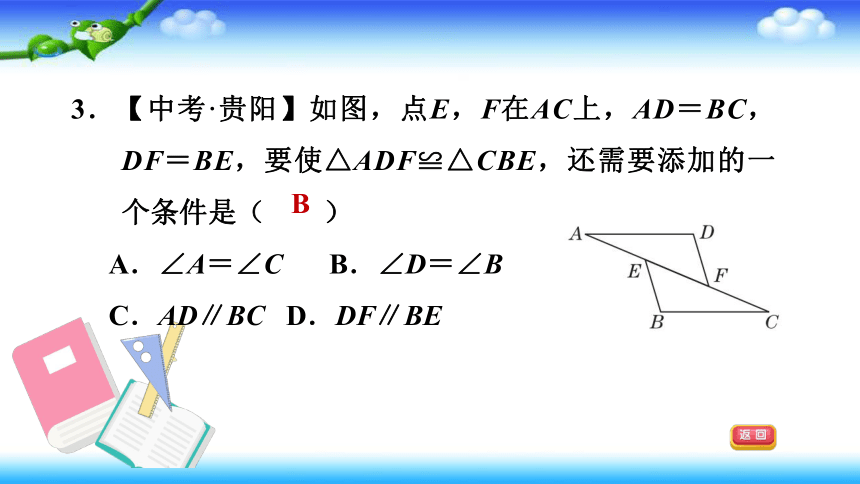
3.【中考·贵阳】如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加的一个条件是( )
A.∠A=∠C
B.∠D=∠B
C.AD∥BC
D.DF∥BE
B
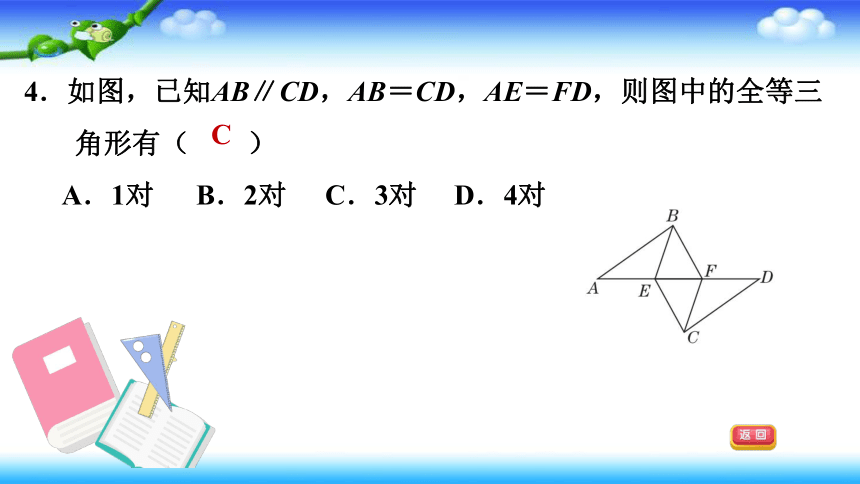
4.如图,已知AB∥CD,AB=CD,AE=FD,则图中的全等三角形有( )
A.1对
B.2对
C.3对
D.4对
C
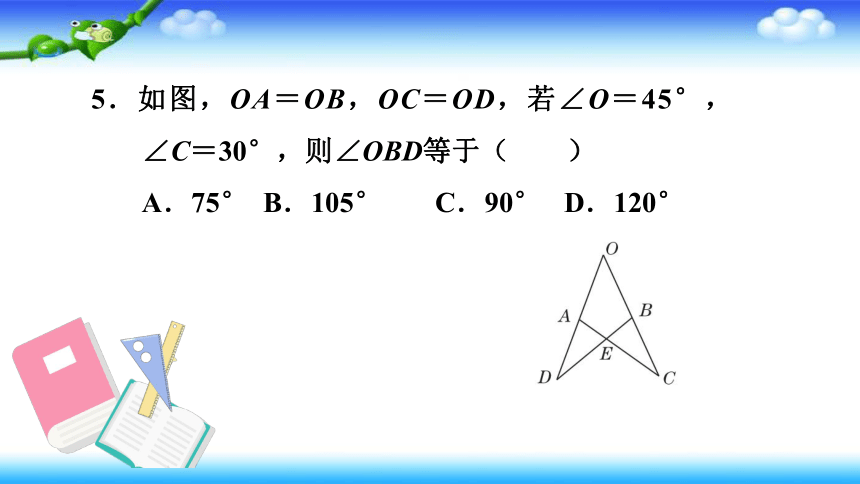
5.如图,OA=OB,OC=OD,若∠O=45°,∠C=30°,则∠OBD等于( )
A.75°
B.105°
C.90°
D.120°
【答案】B
6.【2020·江西】如图,CA平分∠DCB,CB=CD,DA的延长线交BC于点E,若∠EAC=49°,则∠BAE的度数为 .
【点拨】易说明△ABC≌△ADC,从而可得∠B+∠ACB=∠D+∠ACD=49°,进而根据三角形内角和定理求出∠BAC的度数,即可求出∠BAE的度数.
【答案】82°
7.【2020·镇江】如图,AC是四边形ABCD的对角线,∠1=∠B,点E,F分别在AB,BC上,BE=CD,BF=CA,连接EF.
(1)试说明:∠D=∠2;
解:
因为BE=CD,∠1=∠B,BF=CA,
所以△BEF≌△CDA(SAS).
所以∠D=∠2.
(2)若EF∥AC,∠D=78°,求∠BAC的度数.
解:因为∠D=∠2,∠D=78°,
所以∠2=78°.
因为EF∥AC,
所以∠BAC=∠2=78°.
8.如图,在△ABC中,AB=AC,D,E分别是AB,AC的中点,且CD=BE,△ADC与△AEB全等吗?请说明理由.
【点拨】在说明两个三角形全等时,经常会出现用“SSA”判定两个三角形全等的情况.实际上,“SSA”不能判定两个三角形全等.因为两边及一边的对角分别相等的两个三角形不一定全等.如本题中易出现根据条件BE=CD,AB=AC,∠A=∠A,利用“SSA”说明两个三角形全等的错误.
9.【2020·无锡】如图,已知AB∥CD,AB=CD,BE=CF.
(1)试说明:△ABF≌△DCE;
解:因为AB∥CD,所以∠B=∠C.
因为BE=CF,所以BE-EF=CF-EF,即BF=CE.又因为AB=CD,所以△ABF≌△DCE(SAS).
(2)试说明:AF∥DE.
解:因为△ABF≌△DCE,
所以∠AFB=∠DEC.
所以∠AFE=∠DEF.
所以AF∥DE.
10.【2019·乐山】如图,线段AC,BD相交于点E,AE=DE,BE=CE.试说明:∠B=∠C.
11.【2020·宜宾】如图,在△ABC中,点D是边BC的中点,连接AD并延长到点E,使DE=AD,连接CE.
(1)试说明:△ABD≌△ECD;
解:因为点D是边BC的中点,
所以BD=CD.
又因为∠ADB=∠EDC,AD=ED,
所以△ABD≌△ECD(SAS).
(2)若△ABD的面积为5,求△ACE的面积.
解:在△ABC中,点D是边BC的中点,
所以S△ABD=S△ACD.
因为△ABD≌△ECD,
所以S△ABD=S△ECD.
因为S△ABD=5,
所以S△ACE=S△ACD+S△ECD=5+5=10.
12.【2020·徐州】如图,AC⊥BC,DC⊥EC,AC=BC,DC=EC,AE与BD交于点F.
(1)试说明:AE=BD;
解:因为AC⊥BC,DC⊥EC,
所以∠ACB=∠DCE=90°.所以∠ACE=∠BCD.
又因为AC=BC,DC=EC.
所以△ACE≌△BCD(SAS).所以AE=BD.
(2)求∠AFD的度数.
解:如图,BC与AE交于点N.
因为∠ACB=90°,所以∠A+∠ANC=90°.
因为△ACE≌△BCD,所以∠A=∠B.
因为∠ANC=∠BNF,
所以∠B+∠BNF=∠A+∠ANC=90°.
所以∠AFB=90°.所以∠AFD=90°.
谢谢欣赏
THANK
YOU
FOR
LISTENING
第四章
三角形
4.3
探索三角形全等的条件
第3课时
用“
边角边”判定三角形全等
北师大版七年级数学下册
习题课件
4
提示:点击
进入习题
答案显示
6
7
1
2
3
5
B
C
A
82°
8
见习题
见习题
B
B
提示:点击
进入习题
答案显示
10
11
9
见习题
见习题
见习题
12
见习题
1.如图,a,b,c分别表示△ABC的三边长,则下面与△ABC一定全等的三角形是( )
B
2.【2020·永州】如图,已知AB=DC,∠ABC=∠DCB,能直接判定△ABC≌△DCB的方法是( )
A.SAS
B.AAS
C.SSS
D.ASA
A
3.【中考·贵阳】如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加的一个条件是( )
A.∠A=∠C
B.∠D=∠B
C.AD∥BC
D.DF∥BE
B
4.如图,已知AB∥CD,AB=CD,AE=FD,则图中的全等三角形有( )
A.1对
B.2对
C.3对
D.4对
C
5.如图,OA=OB,OC=OD,若∠O=45°,∠C=30°,则∠OBD等于( )
A.75°
B.105°
C.90°
D.120°
【答案】B
6.【2020·江西】如图,CA平分∠DCB,CB=CD,DA的延长线交BC于点E,若∠EAC=49°,则∠BAE的度数为 .
【点拨】易说明△ABC≌△ADC,从而可得∠B+∠ACB=∠D+∠ACD=49°,进而根据三角形内角和定理求出∠BAC的度数,即可求出∠BAE的度数.
【答案】82°
7.【2020·镇江】如图,AC是四边形ABCD的对角线,∠1=∠B,点E,F分别在AB,BC上,BE=CD,BF=CA,连接EF.
(1)试说明:∠D=∠2;
解:
因为BE=CD,∠1=∠B,BF=CA,
所以△BEF≌△CDA(SAS).
所以∠D=∠2.
(2)若EF∥AC,∠D=78°,求∠BAC的度数.
解:因为∠D=∠2,∠D=78°,
所以∠2=78°.
因为EF∥AC,
所以∠BAC=∠2=78°.
8.如图,在△ABC中,AB=AC,D,E分别是AB,AC的中点,且CD=BE,△ADC与△AEB全等吗?请说明理由.
【点拨】在说明两个三角形全等时,经常会出现用“SSA”判定两个三角形全等的情况.实际上,“SSA”不能判定两个三角形全等.因为两边及一边的对角分别相等的两个三角形不一定全等.如本题中易出现根据条件BE=CD,AB=AC,∠A=∠A,利用“SSA”说明两个三角形全等的错误.
9.【2020·无锡】如图,已知AB∥CD,AB=CD,BE=CF.
(1)试说明:△ABF≌△DCE;
解:因为AB∥CD,所以∠B=∠C.
因为BE=CF,所以BE-EF=CF-EF,即BF=CE.又因为AB=CD,所以△ABF≌△DCE(SAS).
(2)试说明:AF∥DE.
解:因为△ABF≌△DCE,
所以∠AFB=∠DEC.
所以∠AFE=∠DEF.
所以AF∥DE.
10.【2019·乐山】如图,线段AC,BD相交于点E,AE=DE,BE=CE.试说明:∠B=∠C.
11.【2020·宜宾】如图,在△ABC中,点D是边BC的中点,连接AD并延长到点E,使DE=AD,连接CE.
(1)试说明:△ABD≌△ECD;
解:因为点D是边BC的中点,
所以BD=CD.
又因为∠ADB=∠EDC,AD=ED,
所以△ABD≌△ECD(SAS).
(2)若△ABD的面积为5,求△ACE的面积.
解:在△ABC中,点D是边BC的中点,
所以S△ABD=S△ACD.
因为△ABD≌△ECD,
所以S△ABD=S△ECD.
因为S△ABD=5,
所以S△ACE=S△ACD+S△ECD=5+5=10.
12.【2020·徐州】如图,AC⊥BC,DC⊥EC,AC=BC,DC=EC,AE与BD交于点F.
(1)试说明:AE=BD;
解:因为AC⊥BC,DC⊥EC,
所以∠ACB=∠DCE=90°.所以∠ACE=∠BCD.
又因为AC=BC,DC=EC.
所以△ACE≌△BCD(SAS).所以AE=BD.
(2)求∠AFD的度数.
解:如图,BC与AE交于点N.
因为∠ACB=90°,所以∠A+∠ANC=90°.
因为△ACE≌△BCD,所以∠A=∠B.
因为∠ANC=∠BNF,
所以∠B+∠BNF=∠A+∠ANC=90°.
所以∠AFB=90°.所以∠AFD=90°.
谢谢欣赏
THANK
YOU
FOR
LISTENING
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
