沪教版(上海)初中数学八年级第一学期 19.8 直角三角形的性质 (2)课件(共19张ppt)
文档属性
| 名称 | 沪教版(上海)初中数学八年级第一学期 19.8 直角三角形的性质 (2)课件(共19张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 515.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 17:26:15 | ||
图片预览


文档简介
直角三角形的两个锐角互余.
直角三角形两直角边的平方和,
等于斜边的平方.
A
C
B
复习回顾
直角三角形的性质:
角:
边:
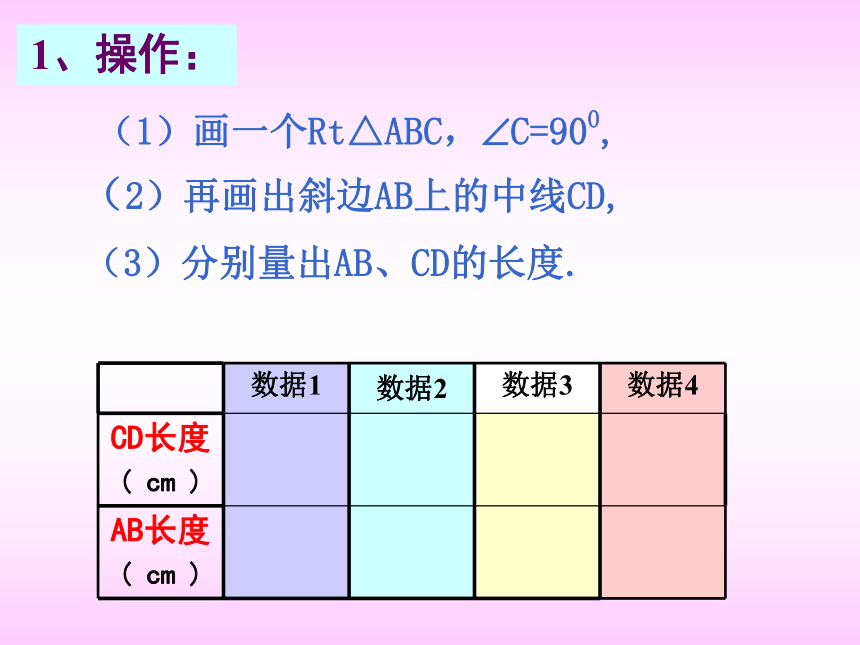
1、操作:
(1)画一个Rt△ABC,?C=900,
(2)再画出斜边AB上的中线CD,
(3)分别量出AB、CD的长度.
数据1
数据2
数据3
数据4
CD长度
( cm )
AB长度
( cm )
C′
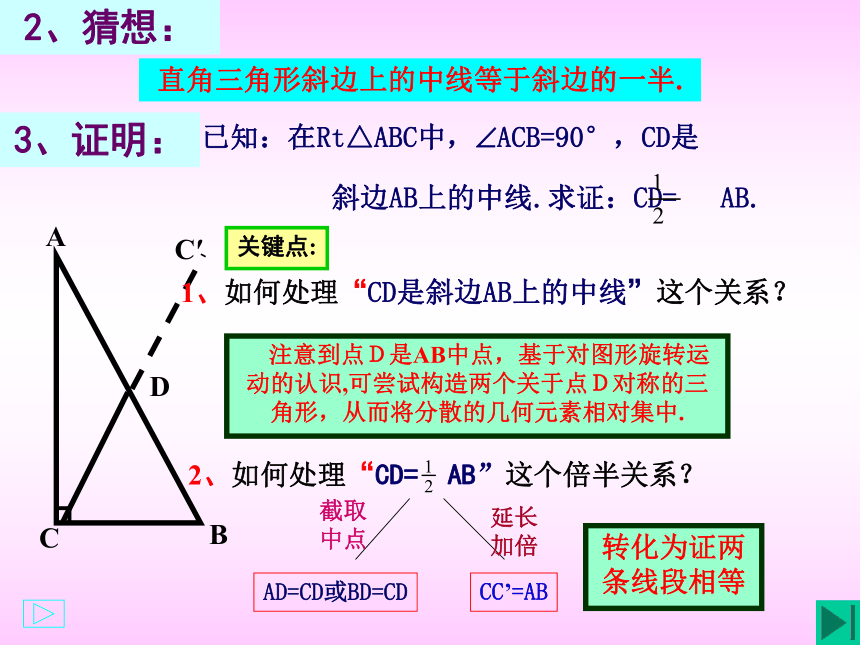
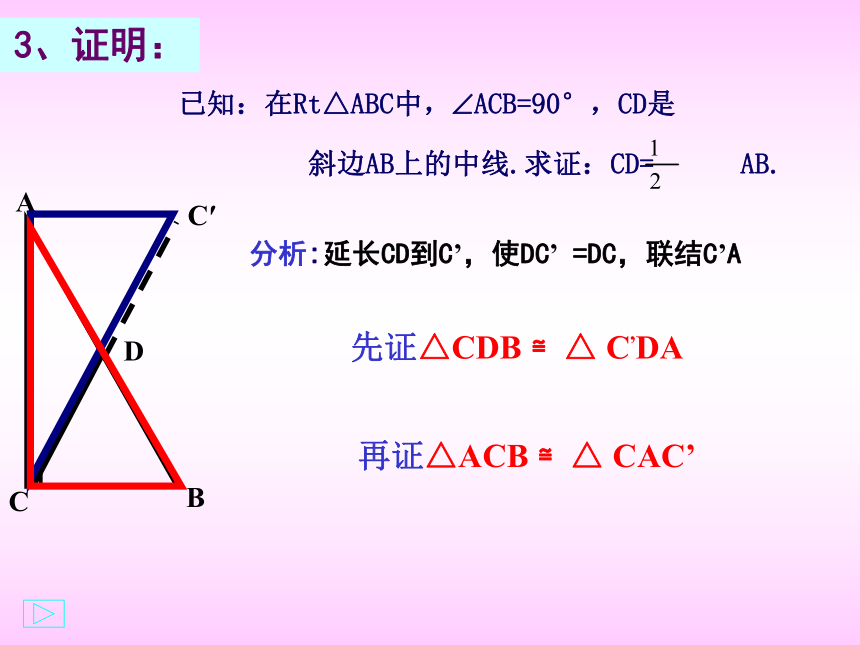
已知:在Rt△ABC中,?ACB=90°,CD是
斜边AB上的中线.求证:CD= AB.
A
C
B
D
3、证明:
2、猜想:
直角三角形斜边上的中线等于斜边的一半.
注意到点D是AB中点,基于对图形旋转运动的认识,可尝试构造两个关于点D对称的三角形,从而将分散的几何元素相对集中.
延长加倍
截取中点
AD=CD或BD=CD
CC’=AB
转化为证两条线段相等
关键点:
1、如何处理“CD是斜边AB上的中线”这个关系?
2、如何处理“CD= AB”这个倍半关系?
分析:延长CD到C’,使DC’ =DC,联结C’A
C′
先证△CDB ≌△ C,DA
再证△ACB ≌△ CAC’
已知:在Rt△ABC中,?ACB=90°,CD是
斜边AB上的中线.求证:CD= AB.
A
C
B
D
3、证明:
AD和BD
∠ACD
5
2a
1、 在Rt△ ABC中 ,∠ACB=900,
CD是AB边上的中线.
(1) 若AB=10 cm , 则CD=____cm;
(2) 若CD= a , 则AB=_____ cm;
(3) 与CD相等的线段是 ;
(4) 与∠A相等的角是_________;
(5) 图中等腰三角形是 ;
(6) 若∠A=30°,则△BCD是 三角形.
小试牛刀
A
C
B
D
△ACD、 △BCD
等边
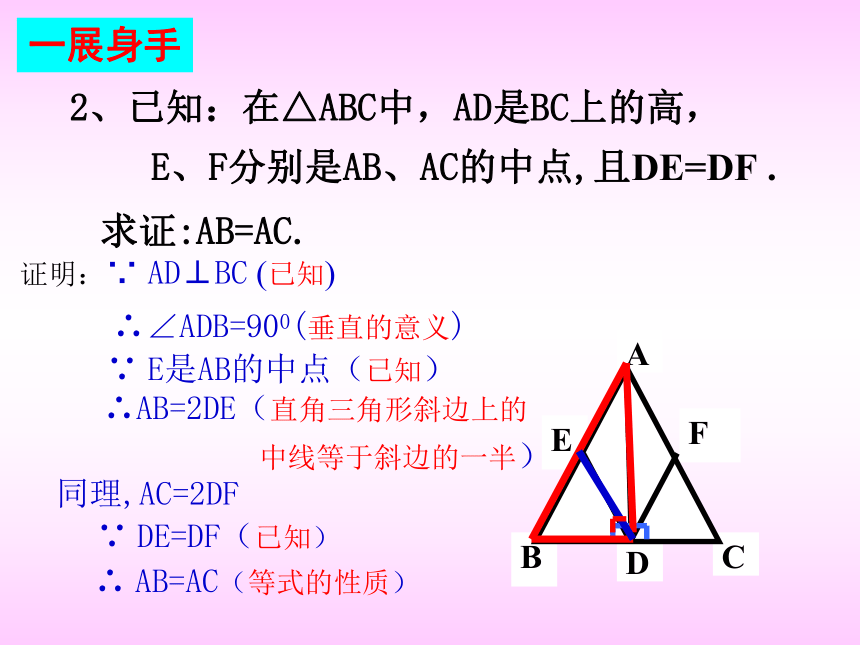
2、已知:在△ABC中,AD是BC上的高,
E、F分别是AB、AC的中点,且DE=DF .
F
C
B
E
A
D
一展身手
求证:AB=AC.
证明:∵ AD⊥BC?(已知)??
∴∠ADB=900(垂直的意义)??
∵?DE=DF(已知)
同理,AC=2DF???
∴AB=2DE(直角三角形斜边上的
中线等于斜边的一半)
∴?AB=AC(等式的性质)
∵?E是AB的中点(已知)
变式已知:在△ABC中, ∠B=∠C,
一展身手
AD平分∠BAC, E、F分别是AB、
AC的中点.
求证: DE=DF.
F
C
B
E
A
D
? 3、已知:∠ADC=∠ABC=90O,E是
AC中点.
求证:∠EDB=∠EBD.
D
A
B
C
E
∟
∟
一展身手
我理解 ……
我掌握 ……
我巩固 ……
我体会 ……
我享受 ……
课堂小结
回家作业
1、直角三角形性质定理2的证明
2、练习册P70页 习题19.8(1) 1、2
3、拓展 书P117页 第3题
A
C
B
D
C′
已知:在Rt△ABC中,?ACB=90°,CD是
斜边AB上的中线.求证:CD= AB.
A
C
B
D
3、证明:
2、猜想:
直角三角形斜边上的中线等于斜边的一半.
注意到点D是AB中点,基于对图形旋转运动的认识,可尝试构造两个关于点D对称的三角形,从而将分散的几何元素相对集中.
延长加倍
截取中点
AD=CD或BD=CD
CC’=AB
转化为证两条线段相等
关键点:
1、如何处理“CD是斜边AB上的中线”这个关系?
2、如何处理“CD= AB”这个倍半关系?
思考题 已知:在△ABC中,BD、CE分
别是边AC、AB上的高,M、N分别是BC、
DE的中点。你知道MN与DE存在怎样的
位置关系?
N
A
B
C
D
E
M
一展身手
2、如图是一副三角板拼成的四边形ABCD,E为BD的中点。小明说点E与点A,C的距离相等,你同意小明的说法吗?
A
B
D
E
C
小试牛刀
1、在Rt△ABC中 ,∠ABC=900,若CD 是AB上的中线,AB=16,你能求出CD的长度吗?
小试牛刀
A
B
C
D
2、在△ABC中,若D是AB边上的中 点,CD=8,你能求出AB的长度吗?
A
C
B
D
小试牛刀
证明:延长CD到点C’,使DC’=CD,联结C’A
已知:在Rt△ABC中,?ACB=90°,CD是斜边AB上的中线。求证:CD= AB
A
C
B
D
C′
在△C’DA和△CDB中
∠C’DA= ∠CDB(对顶角相等)
AD=BD(中线意义)
DC’=DC(所作)
∴ △C’DA≌△CDB(SAS)
∴ C’A=CB(全等三角形的对应边相等)
∠C’DA= ∠B(全等三角形的对应角相等)
∵ ∠BCA=90°(已知)
∠CAB+ ∠B=90 °(直角三角形的两个锐角互余)
∴ ∠CAB+ ∠C’AD=90 °(等量代换)
即∠C’AC=90 °
∴ ∠C’AC= ∠BCA
C’A=BC(已证)
在△C’AC和△BCA中
∠C’AC= ∠BCA(已证)
AC=CA(公共边)
∴ △C’AC≌△BCA(SAS)
∴ C’C=AB(全等三角形的对应边相等)
A
C
B
D
C′
∵ CD= — CC’(所作)
1
2
∴ CD= — AB(等量代换)
1
2
直角三角形两直角边的平方和,
等于斜边的平方.
A
C
B
复习回顾
直角三角形的性质:
角:
边:
1、操作:
(1)画一个Rt△ABC,?C=900,
(2)再画出斜边AB上的中线CD,
(3)分别量出AB、CD的长度.
数据1
数据2
数据3
数据4
CD长度
( cm )
AB长度
( cm )
C′
已知:在Rt△ABC中,?ACB=90°,CD是
斜边AB上的中线.求证:CD= AB.
A
C
B
D
3、证明:
2、猜想:
直角三角形斜边上的中线等于斜边的一半.
注意到点D是AB中点,基于对图形旋转运动的认识,可尝试构造两个关于点D对称的三角形,从而将分散的几何元素相对集中.
延长加倍
截取中点
AD=CD或BD=CD
CC’=AB
转化为证两条线段相等
关键点:
1、如何处理“CD是斜边AB上的中线”这个关系?
2、如何处理“CD= AB”这个倍半关系?
分析:延长CD到C’,使DC’ =DC,联结C’A
C′
先证△CDB ≌△ C,DA
再证△ACB ≌△ CAC’
已知:在Rt△ABC中,?ACB=90°,CD是
斜边AB上的中线.求证:CD= AB.
A
C
B
D
3、证明:
AD和BD
∠ACD
5
2a
1、 在Rt△ ABC中 ,∠ACB=900,
CD是AB边上的中线.
(1) 若AB=10 cm , 则CD=____cm;
(2) 若CD= a , 则AB=_____ cm;
(3) 与CD相等的线段是 ;
(4) 与∠A相等的角是_________;
(5) 图中等腰三角形是 ;
(6) 若∠A=30°,则△BCD是 三角形.
小试牛刀
A
C
B
D
△ACD、 △BCD
等边
2、已知:在△ABC中,AD是BC上的高,
E、F分别是AB、AC的中点,且DE=DF .
F
C
B
E
A
D
一展身手
求证:AB=AC.
证明:∵ AD⊥BC?(已知)??
∴∠ADB=900(垂直的意义)??
∵?DE=DF(已知)
同理,AC=2DF???
∴AB=2DE(直角三角形斜边上的
中线等于斜边的一半)
∴?AB=AC(等式的性质)
∵?E是AB的中点(已知)
变式已知:在△ABC中, ∠B=∠C,
一展身手
AD平分∠BAC, E、F分别是AB、
AC的中点.
求证: DE=DF.
F
C
B
E
A
D
? 3、已知:∠ADC=∠ABC=90O,E是
AC中点.
求证:∠EDB=∠EBD.
D
A
B
C
E
∟
∟
一展身手
我理解 ……
我掌握 ……
我巩固 ……
我体会 ……
我享受 ……
课堂小结
回家作业
1、直角三角形性质定理2的证明
2、练习册P70页 习题19.8(1) 1、2
3、拓展 书P117页 第3题
A
C
B
D
C′
已知:在Rt△ABC中,?ACB=90°,CD是
斜边AB上的中线.求证:CD= AB.
A
C
B
D
3、证明:
2、猜想:
直角三角形斜边上的中线等于斜边的一半.
注意到点D是AB中点,基于对图形旋转运动的认识,可尝试构造两个关于点D对称的三角形,从而将分散的几何元素相对集中.
延长加倍
截取中点
AD=CD或BD=CD
CC’=AB
转化为证两条线段相等
关键点:
1、如何处理“CD是斜边AB上的中线”这个关系?
2、如何处理“CD= AB”这个倍半关系?
思考题 已知:在△ABC中,BD、CE分
别是边AC、AB上的高,M、N分别是BC、
DE的中点。你知道MN与DE存在怎样的
位置关系?
N
A
B
C
D
E
M
一展身手
2、如图是一副三角板拼成的四边形ABCD,E为BD的中点。小明说点E与点A,C的距离相等,你同意小明的说法吗?
A
B
D
E
C
小试牛刀
1、在Rt△ABC中 ,∠ABC=900,若CD 是AB上的中线,AB=16,你能求出CD的长度吗?
小试牛刀
A
B
C
D
2、在△ABC中,若D是AB边上的中 点,CD=8,你能求出AB的长度吗?
A
C
B
D
小试牛刀
证明:延长CD到点C’,使DC’=CD,联结C’A
已知:在Rt△ABC中,?ACB=90°,CD是斜边AB上的中线。求证:CD= AB
A
C
B
D
C′
在△C’DA和△CDB中
∠C’DA= ∠CDB(对顶角相等)
AD=BD(中线意义)
DC’=DC(所作)
∴ △C’DA≌△CDB(SAS)
∴ C’A=CB(全等三角形的对应边相等)
∠C’DA= ∠B(全等三角形的对应角相等)
∵ ∠BCA=90°(已知)
∠CAB+ ∠B=90 °(直角三角形的两个锐角互余)
∴ ∠CAB+ ∠C’AD=90 °(等量代换)
即∠C’AC=90 °
∴ ∠C’AC= ∠BCA
C’A=BC(已证)
在△C’AC和△BCA中
∠C’AC= ∠BCA(已证)
AC=CA(公共边)
∴ △C’AC≌△BCA(SAS)
∴ C’C=AB(全等三角形的对应边相等)
A
C
B
D
C′
∵ CD= — CC’(所作)
1
2
∴ CD= — AB(等量代换)
1
2
