沪教版(上海)初中数学九年级第一学期 24.2 平行线分线段成比例定理 课件(共22张ppt)
文档属性
| 名称 | 沪教版(上海)初中数学九年级第一学期 24.2 平行线分线段成比例定理 课件(共22张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 555.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 00:00:00 | ||
图片预览



文档简介
平行线分线段成比例定理
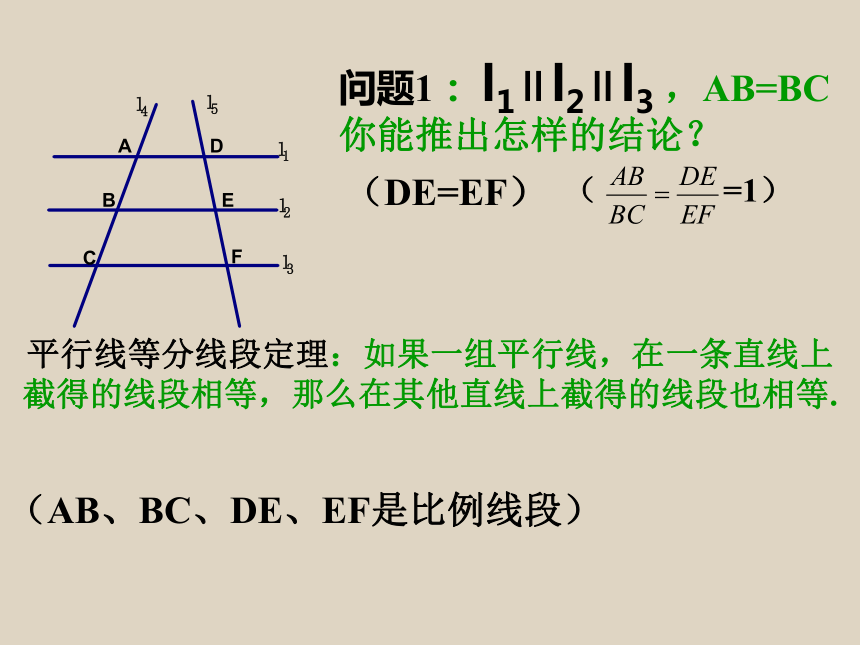
平行线等分线段定理:如果一组平行线,在一条直线上
截得的线段相等,那么在其他直线上截得的线段也相等.
问题1:
l1∥l2∥l3
,AB=BC你能推出怎样的结论?
(DE=EF)
(AB、BC、DE、EF是比例线段)
(
=1)
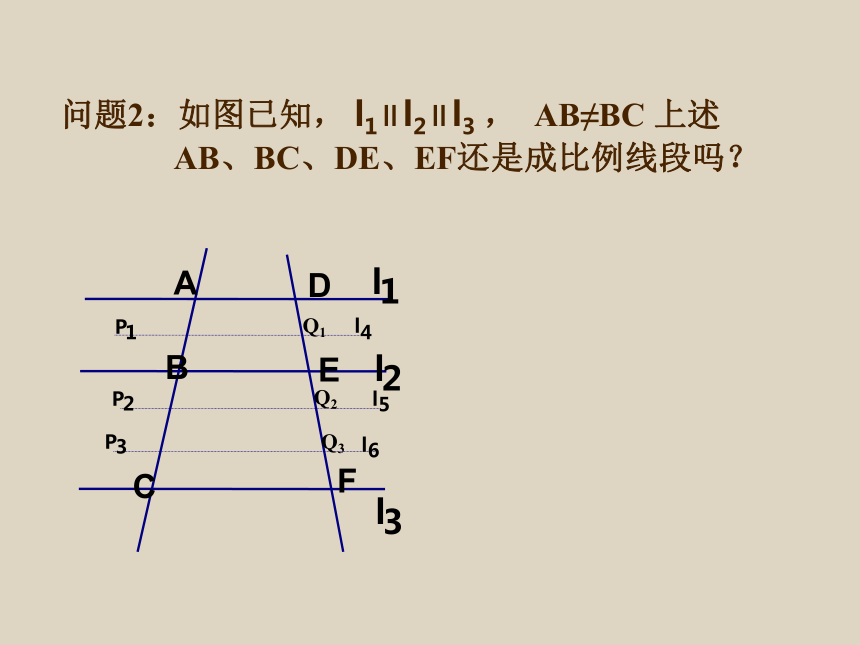
问题2:如图已知,
l1∥l2∥l3
,
AB≠BC
上述
AB、BC、DE、EF还是成比例线段吗?
l
3
l
2
l
1
F
E
D
C
B
A
l
4
P
1
Q1
l
5
P
2
Q2
l
6
P
3
Q3
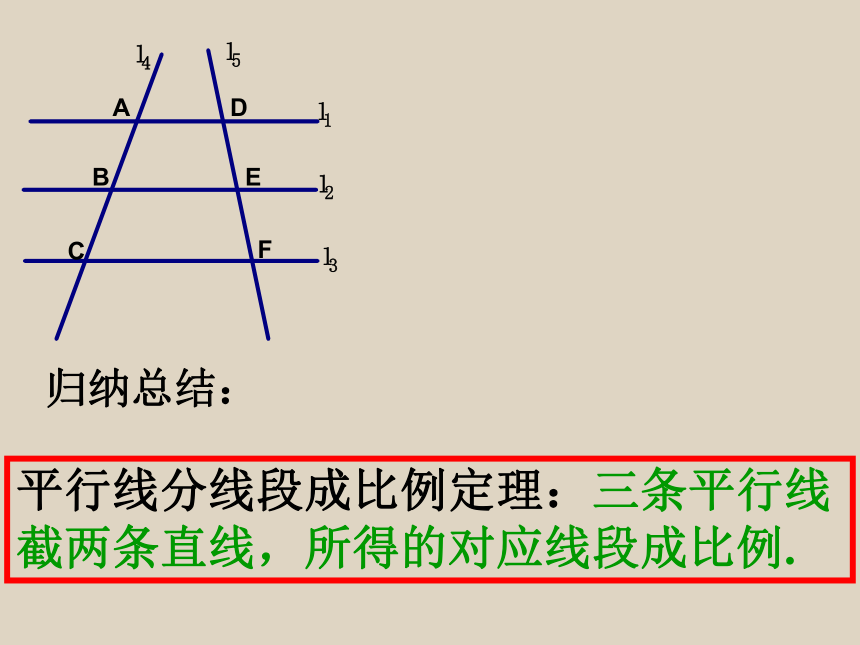
平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.
归纳总结:
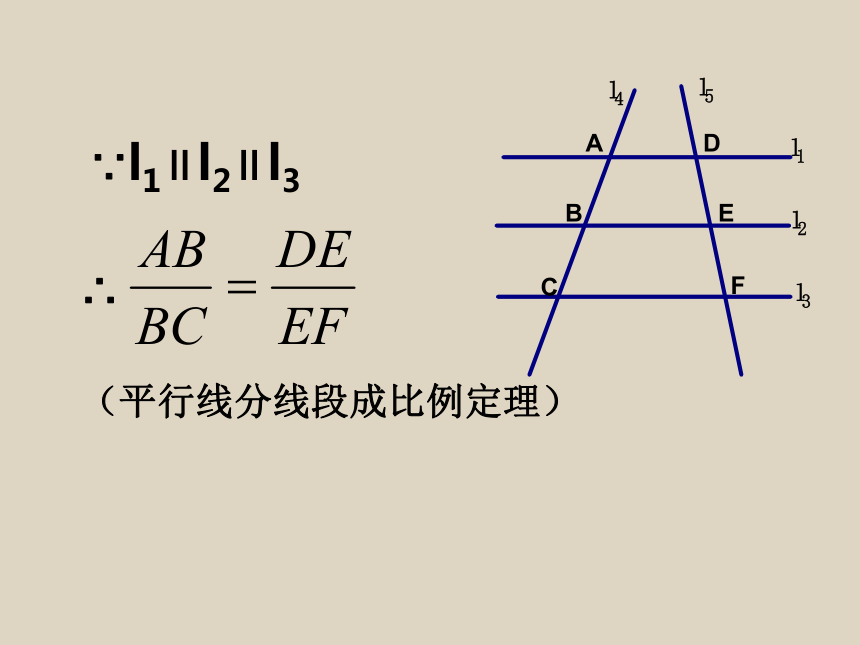
∵l1∥l2∥l3
∴
(平行线分线段成比例定理)
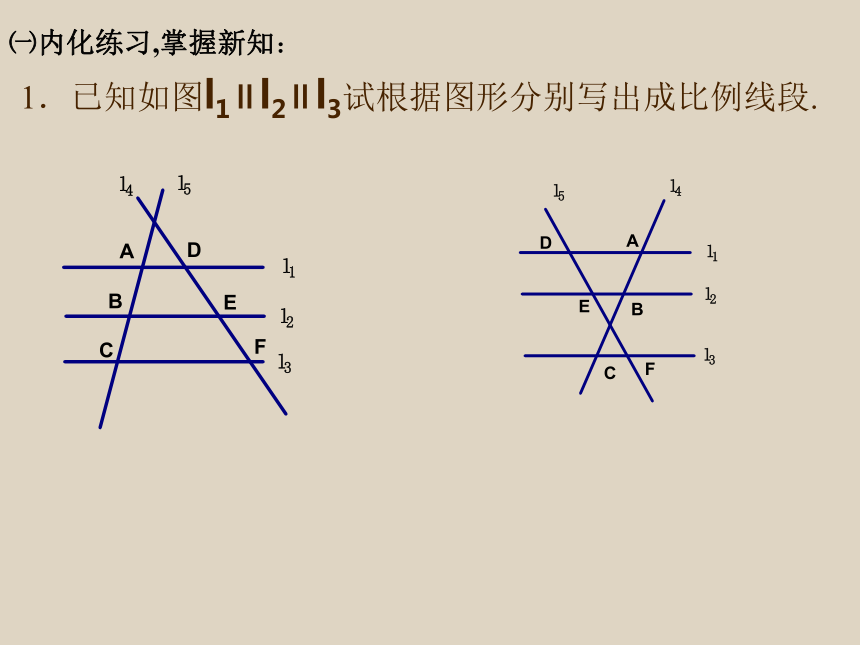
1.已知如图l1∥l2∥l3试根据图形分别写出成比例线段.
㈠内化练习,掌握新知:
2.已知如图
(1)下列比例式中正确的是(
).
(A)
(B)
(C)
(D)
(2)若AB=2
,
,则BC长为
.
C
4
l1∥l2∥l3
例1
已知如图l1∥l2∥l3
,AB=3,
DE=2,EF=4,求
BC
.
∴BC
=6
㈡例题讲解,应用新知:
∵l1∥l2∥l3
,
∴
(平行线分线段成比例定理)
解:
即
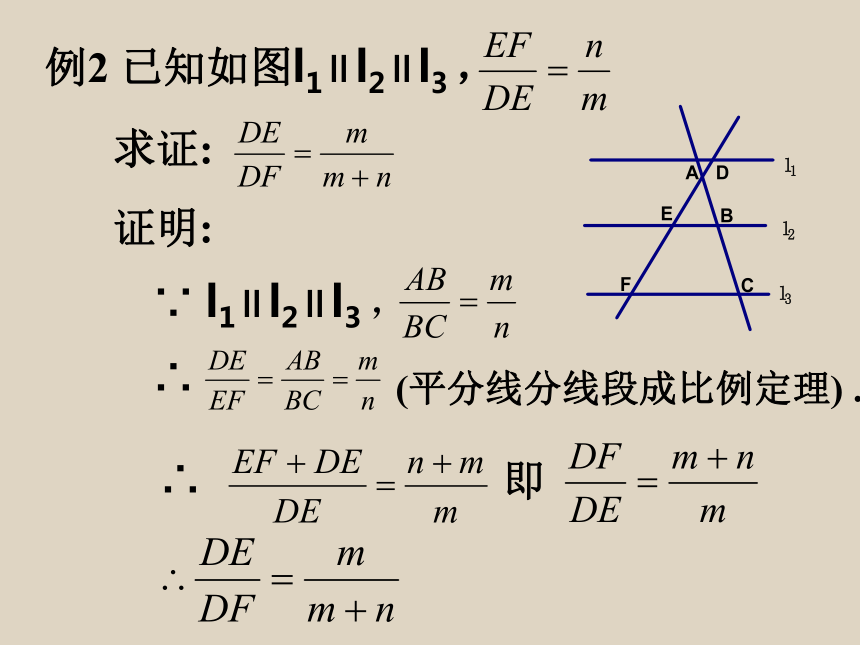
例2
已知如图l1∥l2∥l3
,
求证:
∵
l1∥l2∥l3
,
∴
(平分线分线段成比例定理)
.
证明:
即
∴
1.已知如图l1∥l2∥l3
求证:
巩固训练:
2.
已知如图l1∥l2∥l3
,BD=2AB,EF=3,HF=5,求FG和HQ的长
.
l
3
l
2
l
1
E
D
C
B
A
如图l1∥l2∥l3试根据图形分别写出成比例线段.
创设情境,拓展新知:
推论
平行于三角形一边的直线截其他两边(或两边的延长线),所得得对应线段成比例.
1.已知:如图,点E在平行四边形ABCD的边AB的延长线上,DE分别交AC、BC于点F、G,在该图中找出三个“平行线分线段成比例定理的推论”的图形,分别把它们一一画出来
㈠内化练习,掌握新知:
?
?
2.已知如图,DE∥BC
(1)判断下列比例式是否正确(正确的打“√”,错误的打“×”)
(
)
②
(
)
③
(
)
④
(
)
?
(2)若AB=14,AC=18,AE=10,则AD=
.
√
×
√
√
例3
已知:如图DE∥BC,AB=15,AC=9,BD=4,求:AE
解:∵DE∥BC,
∴
(平行于三角形一边的直线截其他两边,所得的对应线段成比例),
即
∴CE=
∴AE=AC+CE=9+
=
?
㈡例题讲解,应用新知:
1.已知如图,点E是平行四边形ABCD得边AB的延长线上的一点,DE交BC于点F,
,EF=3
,BF=2,求DF、BC的长
又∵EF=3,BF=2,ED=EF+FD=3+9=12
∴
∴BC=8
?
在平行四边形ABCD中,AD∥BC,即BF∥AD
∴
(平行于三角形一边的直线截其他两边,所得的对应线段成比例)
又∵
,EF=3,
∴
,∴FD=9
∵BE∥CD,
∴
(平行于三角形一边的直线截其
他两边的延长线所得的对应线段成比例)
解:
证明:
2.已知:如图,G是五边形ABCDE对角线AC上一点,过点
G作GE∥BC,HG∥DC,分别交AD、AB于F、H
求证:
∵FG∥BC
∴
(平行于三角形一边的直线截其他两边,所得的
对应线段成比例)
又∵AE∥GH∥CD
∴
(平行线分线段成比例定理)
∴
课堂小结:本节课我们学行线分线段成比例定理及其推论,不仅要能正确地叙述这个定理和推论,而且要能结合图形用符号语言表示定理和推论:
?
平行于三角形一边的直线截其他两边(或两边的延长线),所得得对应线段成比例.
定理名称
文
字
语
言
图
形
符号语言
平行线分线段成比例定理
?
平行线分线段成比例定理的推论
?
?
?
三条平行线截两条直
线,所得的对应线段
成比例.
作业布置:练习册
?
同学们再见
平行线等分线段定理:如果一组平行线,在一条直线上
截得的线段相等,那么在其他直线上截得的线段也相等.
问题1:
l1∥l2∥l3
,AB=BC你能推出怎样的结论?
(DE=EF)
(AB、BC、DE、EF是比例线段)
(
=1)
问题2:如图已知,
l1∥l2∥l3
,
AB≠BC
上述
AB、BC、DE、EF还是成比例线段吗?
l
3
l
2
l
1
F
E
D
C
B
A
l
4
P
1
Q1
l
5
P
2
Q2
l
6
P
3
Q3
平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.
归纳总结:
∵l1∥l2∥l3
∴
(平行线分线段成比例定理)
1.已知如图l1∥l2∥l3试根据图形分别写出成比例线段.
㈠内化练习,掌握新知:
2.已知如图
(1)下列比例式中正确的是(
).
(A)
(B)
(C)
(D)
(2)若AB=2
,
,则BC长为
.
C
4
l1∥l2∥l3
例1
已知如图l1∥l2∥l3
,AB=3,
DE=2,EF=4,求
BC
.
∴BC
=6
㈡例题讲解,应用新知:
∵l1∥l2∥l3
,
∴
(平行线分线段成比例定理)
解:
即
例2
已知如图l1∥l2∥l3
,
求证:
∵
l1∥l2∥l3
,
∴
(平分线分线段成比例定理)
.
证明:
即
∴
1.已知如图l1∥l2∥l3
求证:
巩固训练:
2.
已知如图l1∥l2∥l3
,BD=2AB,EF=3,HF=5,求FG和HQ的长
.
l
3
l
2
l
1
E
D
C
B
A
如图l1∥l2∥l3试根据图形分别写出成比例线段.
创设情境,拓展新知:
推论
平行于三角形一边的直线截其他两边(或两边的延长线),所得得对应线段成比例.
1.已知:如图,点E在平行四边形ABCD的边AB的延长线上,DE分别交AC、BC于点F、G,在该图中找出三个“平行线分线段成比例定理的推论”的图形,分别把它们一一画出来
㈠内化练习,掌握新知:
?
?
2.已知如图,DE∥BC
(1)判断下列比例式是否正确(正确的打“√”,错误的打“×”)
(
)
②
(
)
③
(
)
④
(
)
?
(2)若AB=14,AC=18,AE=10,则AD=
.
√
×
√
√
例3
已知:如图DE∥BC,AB=15,AC=9,BD=4,求:AE
解:∵DE∥BC,
∴
(平行于三角形一边的直线截其他两边,所得的对应线段成比例),
即
∴CE=
∴AE=AC+CE=9+
=
?
㈡例题讲解,应用新知:
1.已知如图,点E是平行四边形ABCD得边AB的延长线上的一点,DE交BC于点F,
,EF=3
,BF=2,求DF、BC的长
又∵EF=3,BF=2,ED=EF+FD=3+9=12
∴
∴BC=8
?
在平行四边形ABCD中,AD∥BC,即BF∥AD
∴
(平行于三角形一边的直线截其他两边,所得的对应线段成比例)
又∵
,EF=3,
∴
,∴FD=9
∵BE∥CD,
∴
(平行于三角形一边的直线截其
他两边的延长线所得的对应线段成比例)
解:
证明:
2.已知:如图,G是五边形ABCDE对角线AC上一点,过点
G作GE∥BC,HG∥DC,分别交AD、AB于F、H
求证:
∵FG∥BC
∴
(平行于三角形一边的直线截其他两边,所得的
对应线段成比例)
又∵AE∥GH∥CD
∴
(平行线分线段成比例定理)
∴
课堂小结:本节课我们学行线分线段成比例定理及其推论,不仅要能正确地叙述这个定理和推论,而且要能结合图形用符号语言表示定理和推论:
?
平行于三角形一边的直线截其他两边(或两边的延长线),所得得对应线段成比例.
定理名称
文
字
语
言
图
形
符号语言
平行线分线段成比例定理
?
平行线分线段成比例定理的推论
?
?
?
三条平行线截两条直
线,所得的对应线段
成比例.
作业布置:练习册
?
同学们再见
