沪教版(上海)初中数学九年级第一学期 24.4 相似三角形的判定 课件 (1)(共20张ppt)
文档属性
| 名称 | 沪教版(上海)初中数学九年级第一学期 24.4 相似三角形的判定 课件 (1)(共20张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 921.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 00:00:00 | ||
图片预览



文档简介
§24.4相似三角形的判定(1)
一、复习引入
形状相同的两个图形
今天我们来研究其中比较特殊的情况
相似三角形
1、什么是相似形?
2、相似形有什么性质?
若两个图形是相似形,那么它们的对应角 ,对应边的长度 .
相等
成比例
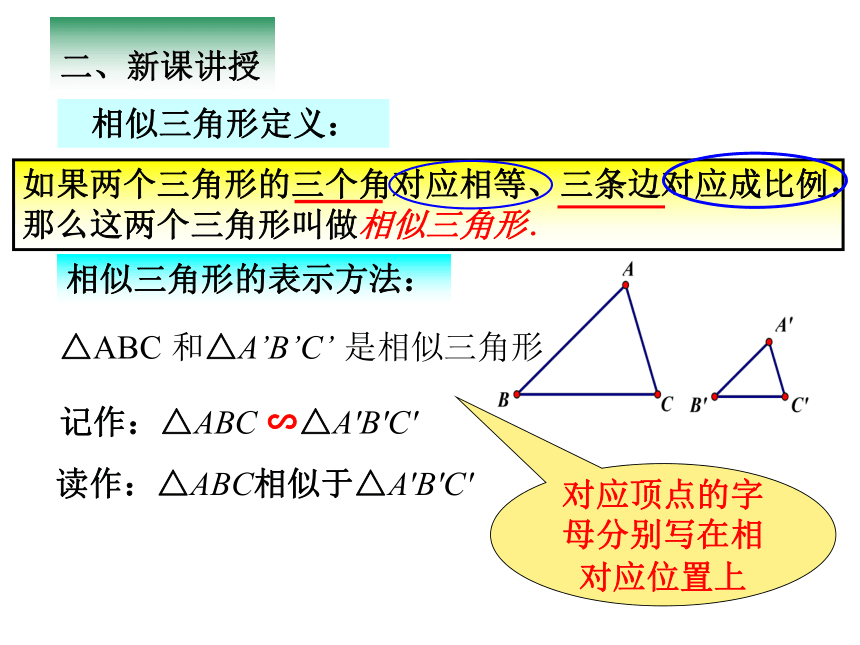
相似三角形定义:
如果两个三角形的三个角对应相等、三条边对应成比例,那么这两个三角形叫做相似三角形.
相似三角形的表示方法:
记作:△ABC ∽△A'B'C'
对应顶点的字母分别写在相对应位置上
△ABC 和△A’B’C’ 是相似三角形
读作:△ABC相似于△A'B'C'
二、新课讲授
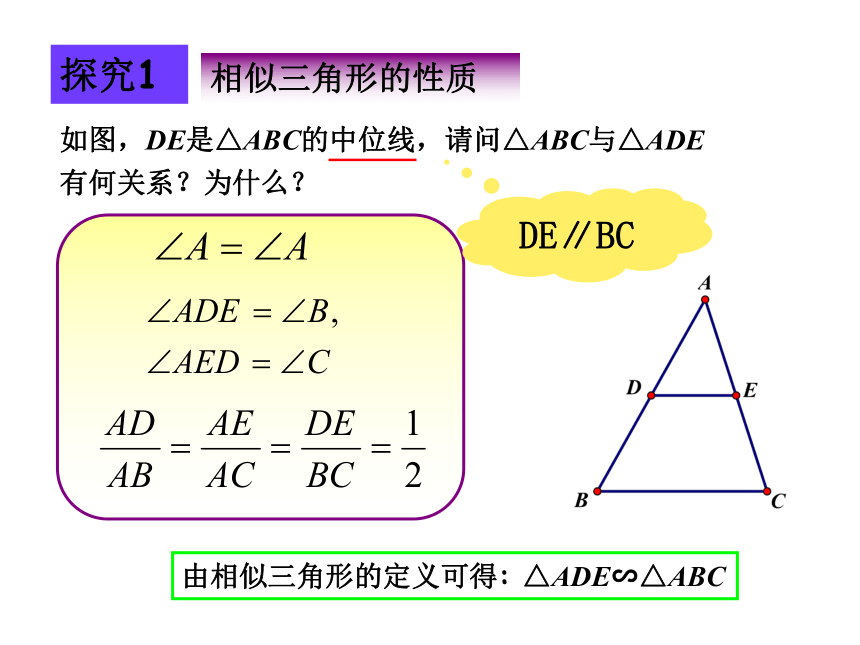
如图,DE是△ABC的中位线,请问△ABC与△ADE有何关系?为什么?
探究1
相似三角形的性质
由相似三角形的定义可得: △ADE∽△ABC
DE∥BC
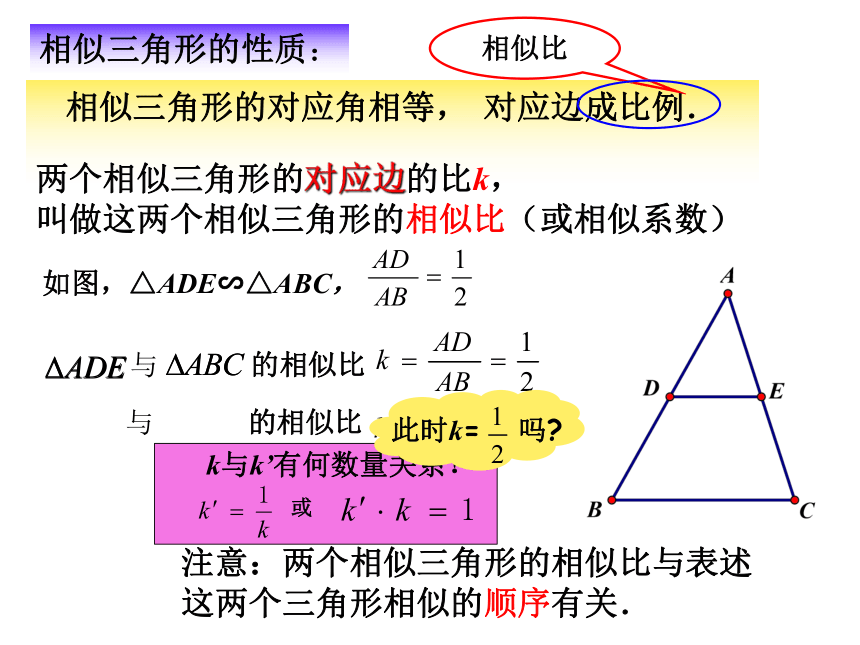
相似三角形的对应角相等, 对应边成比例.
相似比
两个相似三角形的对应边的比k,
叫做这两个相似三角形的相似比(或相似系数)
如图,△ADE∽△ABC,
与
的相似比
k与k’有何数量关系?
注意:两个相似三角形的相似比与表述这两个三角形相似的顺序有关.
或
相似三角形的性质:
与
的相似比
此时k= 吗?
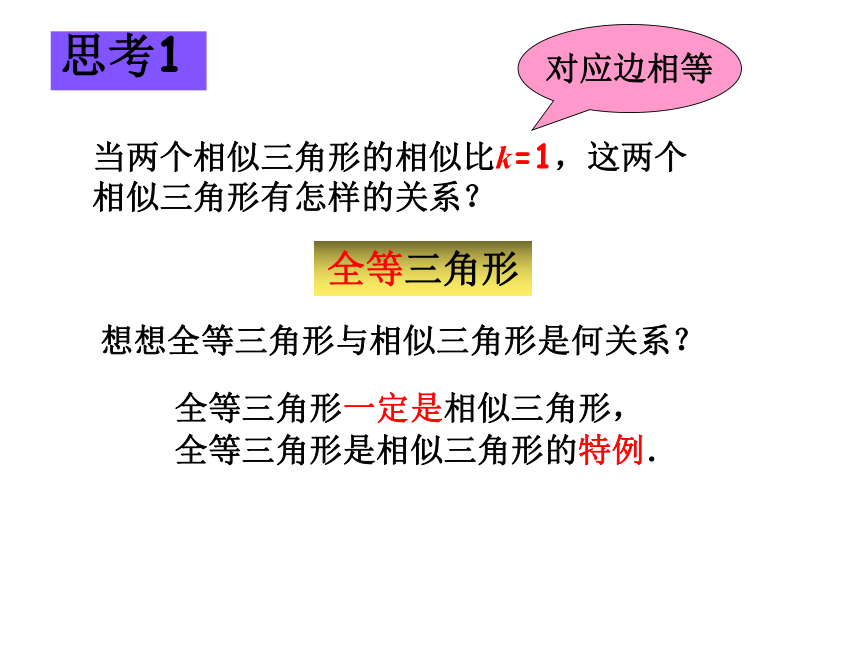
当两个相似三角形的相似比k=1,这两个相似三角形有怎样的关系?
全等三角形
想想全等三角形与相似三角形是何关系?
全等三角形一定是相似三角形,
全等三角形是相似三角形的特例.
思考1
对应边相等
?
?
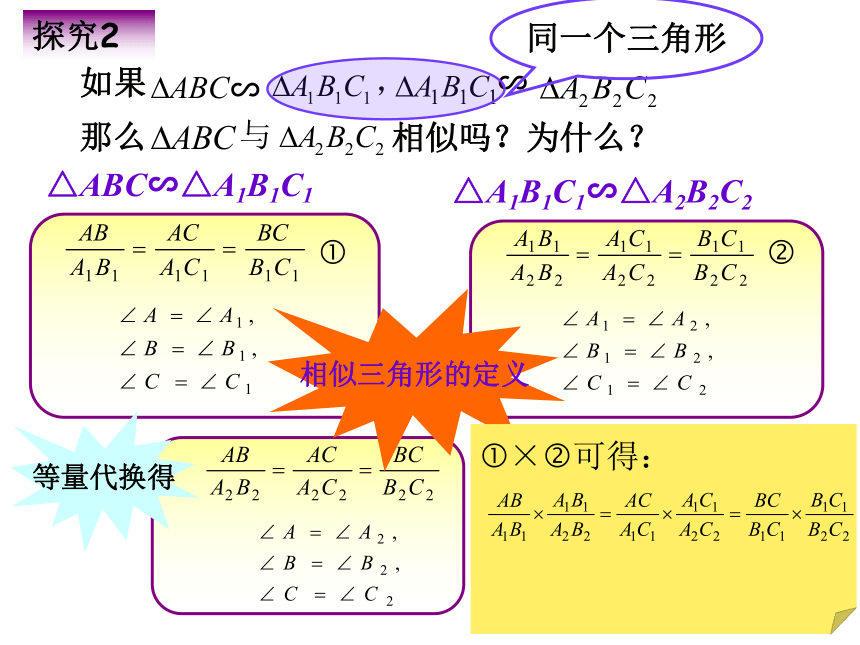
如果
∽
,
∽
那么
与
相似吗?为什么?
探究2
△ABC∽△A1B1C1
△A1B1C1∽△A2B2C2
△ABC∽△A2B2C2
相似三角形的定义
同一个三角形
?×?可得:
等量代换得
如果两个三角形分别与同一个三角形相似,那么这两个三角形也相似.
∽
,
∽
∴
∽
(相似三角形的传递性)
相似三角形具有传递性
(判定方法)
符号语言:
∵
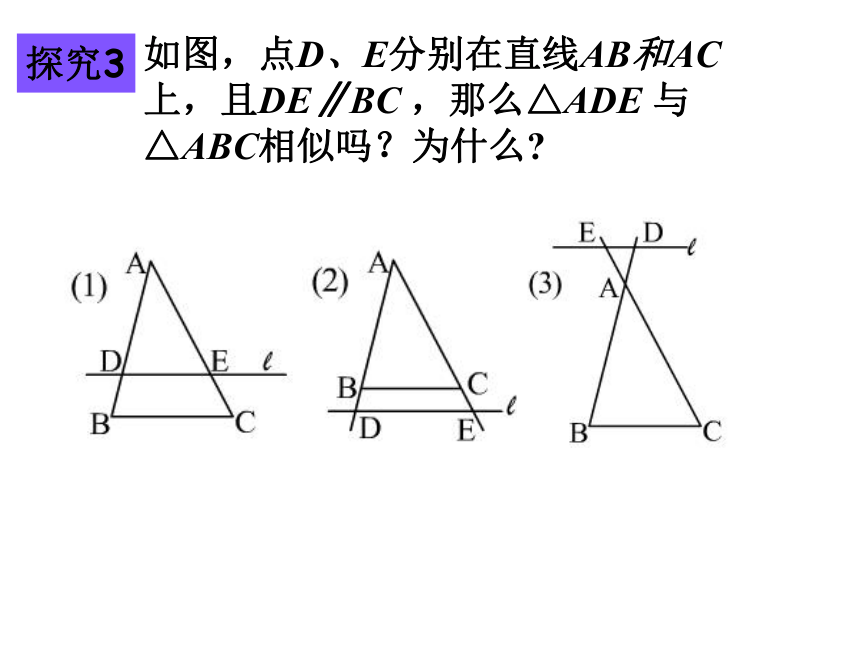
如图,点D、E分别在直线AB和AC上,且DE∥BC ,那么△ADE 与 △ABC相似吗?为什么?
探究3
对应角相等,
对应边成比例
相似三角形的定义
探究3
证明: ∵DE∥BC
∽
已知:如图,DE∥BC ,那么△ADE 与 △ABC相似吗?为什么?
如果点D、E分别在直线AB和AC上,且DE∥BC ,那么△ADE 与 △ABC还相似吗?为什么?
探究3
同理可证: △ADE ∽ △ABC
平行于三角形一边的直线截其他两边所在的直线,截得的三角形与原三角形相似.
∵ DE∥BC
∽
(相似三角形的预备定理)
符号表达:
相似三角形的预备定理:
归纳小结:
一边
直线
适时小结:
一是定义法;
三是预备定理.
掌握了证明三角形相似的三种方法:
二是传递性;
1、如图:E是平行四边形ABCD的边BA延长线上的一点,CE交AD于点F.图中有那几对相似三角形?
∵AB∥CD
∵AD∥BC
∴△AFE∽△BCE
E
A
F
B
C
E
A
D
F
C
∴△AFE∽△DFC
由相似传递性可得:
△DFC∽△BCE
课堂练习:
课堂练习:
2、如图:△ABC∽△AED,AG=3,AD=6,AF=2,EF=6,则△AFG与△ABC相似吗? 为什么?
课堂小结:
本节课主要学习了什么,有何收获?
1、相似三角形的定义.
2、相似三角形的性质.
课堂小结:
3、相似三角形的判定方法:
①相似三角形的传递性;
②相似三角形的预备定理;
∽
,
∽
∴
∽
∵
∵ DE∥BC
∽
课堂小结:
3、相似三角形的判定方法:
①相似三角形的传递性;
②相似三角形的预备定理;
A
∽
,
∽
∴
∽
∵
∵ DE∥BC
∽
3、相似三角形的判定方法:
①相似三角形的传递性;
②相似三角形的预备定理;
∽
,
∽
∴
∽
∵
∵ DE∥BC
∽
课堂小结:
布置作业:练习册24.4(1)
一、复习引入
形状相同的两个图形
今天我们来研究其中比较特殊的情况
相似三角形
1、什么是相似形?
2、相似形有什么性质?
若两个图形是相似形,那么它们的对应角 ,对应边的长度 .
相等
成比例
相似三角形定义:
如果两个三角形的三个角对应相等、三条边对应成比例,那么这两个三角形叫做相似三角形.
相似三角形的表示方法:
记作:△ABC ∽△A'B'C'
对应顶点的字母分别写在相对应位置上
△ABC 和△A’B’C’ 是相似三角形
读作:△ABC相似于△A'B'C'
二、新课讲授
如图,DE是△ABC的中位线,请问△ABC与△ADE有何关系?为什么?
探究1
相似三角形的性质
由相似三角形的定义可得: △ADE∽△ABC
DE∥BC
相似三角形的对应角相等, 对应边成比例.
相似比
两个相似三角形的对应边的比k,
叫做这两个相似三角形的相似比(或相似系数)
如图,△ADE∽△ABC,
与
的相似比
k与k’有何数量关系?
注意:两个相似三角形的相似比与表述这两个三角形相似的顺序有关.
或
相似三角形的性质:
与
的相似比
此时k= 吗?
当两个相似三角形的相似比k=1,这两个相似三角形有怎样的关系?
全等三角形
想想全等三角形与相似三角形是何关系?
全等三角形一定是相似三角形,
全等三角形是相似三角形的特例.
思考1
对应边相等
?
?
如果
∽
,
∽
那么
与
相似吗?为什么?
探究2
△ABC∽△A1B1C1
△A1B1C1∽△A2B2C2
△ABC∽△A2B2C2
相似三角形的定义
同一个三角形
?×?可得:
等量代换得
如果两个三角形分别与同一个三角形相似,那么这两个三角形也相似.
∽
,
∽
∴
∽
(相似三角形的传递性)
相似三角形具有传递性
(判定方法)
符号语言:
∵
如图,点D、E分别在直线AB和AC上,且DE∥BC ,那么△ADE 与 △ABC相似吗?为什么?
探究3
对应角相等,
对应边成比例
相似三角形的定义
探究3
证明: ∵DE∥BC
∽
已知:如图,DE∥BC ,那么△ADE 与 △ABC相似吗?为什么?
如果点D、E分别在直线AB和AC上,且DE∥BC ,那么△ADE 与 △ABC还相似吗?为什么?
探究3
同理可证: △ADE ∽ △ABC
平行于三角形一边的直线截其他两边所在的直线,截得的三角形与原三角形相似.
∵ DE∥BC
∽
(相似三角形的预备定理)
符号表达:
相似三角形的预备定理:
归纳小结:
一边
直线
适时小结:
一是定义法;
三是预备定理.
掌握了证明三角形相似的三种方法:
二是传递性;
1、如图:E是平行四边形ABCD的边BA延长线上的一点,CE交AD于点F.图中有那几对相似三角形?
∵AB∥CD
∵AD∥BC
∴△AFE∽△BCE
E
A
F
B
C
E
A
D
F
C
∴△AFE∽△DFC
由相似传递性可得:
△DFC∽△BCE
课堂练习:
课堂练习:
2、如图:△ABC∽△AED,AG=3,AD=6,AF=2,EF=6,则△AFG与△ABC相似吗? 为什么?
课堂小结:
本节课主要学习了什么,有何收获?
1、相似三角形的定义.
2、相似三角形的性质.
课堂小结:
3、相似三角形的判定方法:
①相似三角形的传递性;
②相似三角形的预备定理;
∽
,
∽
∴
∽
∵
∵ DE∥BC
∽
课堂小结:
3、相似三角形的判定方法:
①相似三角形的传递性;
②相似三角形的预备定理;
A
∽
,
∽
∴
∽
∵
∵ DE∥BC
∽
3、相似三角形的判定方法:
①相似三角形的传递性;
②相似三角形的预备定理;
∽
,
∽
∴
∽
∵
∵ DE∥BC
∽
课堂小结:
布置作业:练习册24.4(1)
