沪教版(上海)初中数学九年级第一学期 24.4 相似三角形的判定 课件(共20张ppt)
文档属性
| 名称 | 沪教版(上海)初中数学九年级第一学期 24.4 相似三角形的判定 课件(共20张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 904.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 17:36:02 | ||
图片预览






文档简介
相似三角形的判定
我们现在判定两个三角形是否相似,必须要知道它们的对应角是否相等,对应边是否成比例.那么是否存在判定两个三角形相似的简便方法呢?
我们在判断两个三角形全等时,使用了哪些方法?判断三角形相似是否有类似的方法呢?
这两个三角形的三个内角的大小有什么关系?
三个内角对应相等的两个三角形一定相似吗?
三个内角对应相等。
观察你与老师的直角三角尺 ,会相似吗?
(30O 与60O)
相
似
画一个三角形 ,使三个角分别为60°,45°, 75° 。
①同桌分别量出两个三角形三边的长度;
②同桌这两个三角形相似吗?换另三个角试试?
即: 如果一个三角形的三个角分别与另一个三角形的三个角对应相等,那么这两个三角形_______.
相似
一定需三个角吗?
观察
C
A
A'
B
B'
C'
∵ ∠A=∠A', ∠B=∠B'
∴ ΔABC ∽ ΔA'B'C'
用数学符号表示:
相似三角形的识别
相似三角形判定定理1:如果一个三角形的两个角分别与另一个三角形的两个角对应相等,那么这两个三角形相似。 (可简单说成:两角对应相等的两个三角形相似)
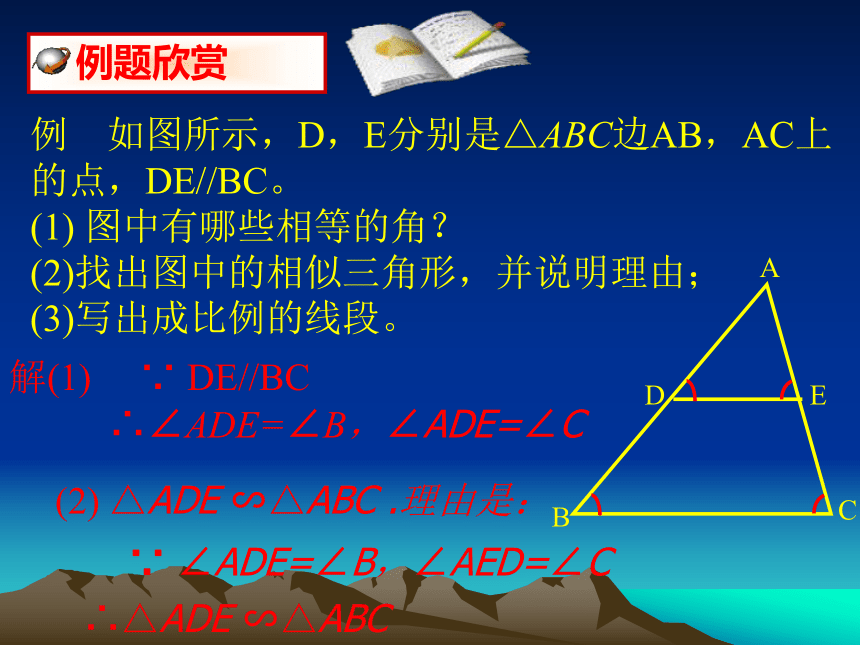
例 如图所示,D,E分别是△ABC边AB,AC上的点,DE//BC。
(1) 图中有哪些相等的角?
(2)找出图中的相似三角形,并说明理由;
(3)写出成比例的线段。
例题欣赏
解(1) ∵ DE//BC
∴∠ADE=∠B,∠ADE=∠C
(2) △ADE ∽△ABC .理由是:
∵ ∠ADE=∠B,∠AED=∠C
∴△ADE ∽△ABC
A
E
B
C
D
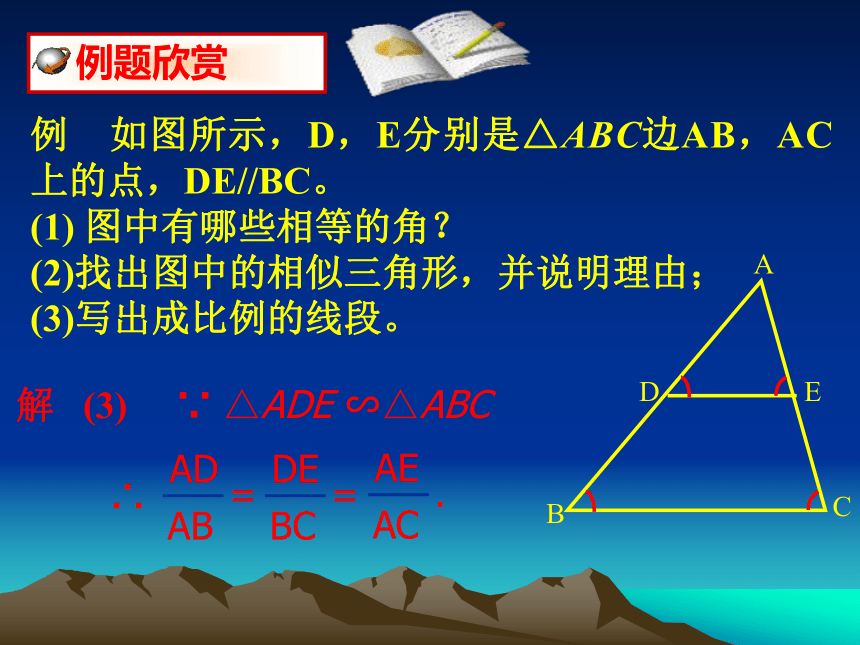
例 如图所示,D,E分别是△ABC边AB,AC上的点,DE//BC。
(1) 图中有哪些相等的角?
(2)找出图中的相似三角形,并说明理由;
(3)写出成比例的线段。
例题欣赏
解 (3) ∵ △ADE ∽△ABC
A
E
B
C
D
∴
AD
AB
=
DE
BC
=
AE
AC
.
例题欣赏
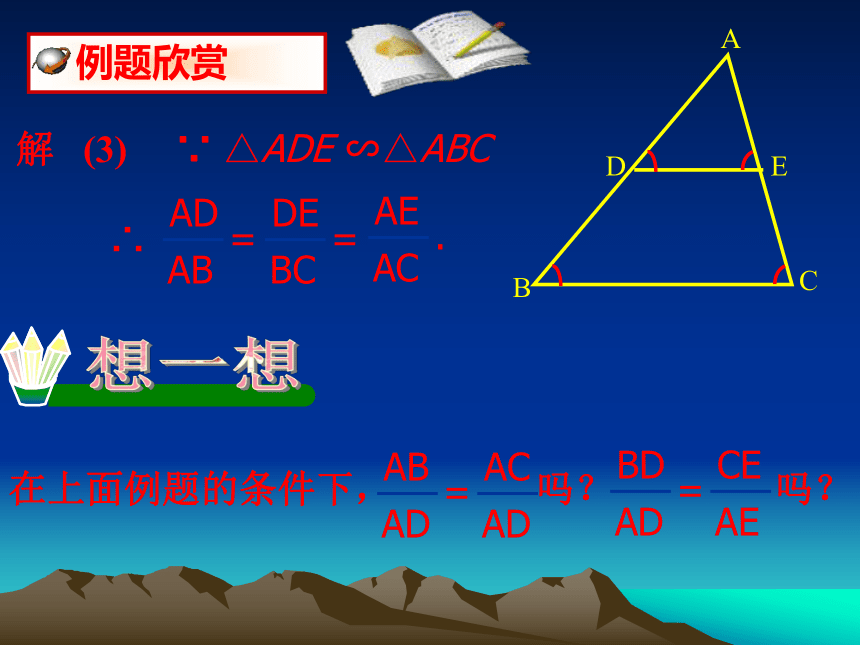
解 (3) ∵ △ADE ∽△ABC
A
E
B
C
D
∴
AD
AB
=
DE
BC
=
AE
AC
.
在上面例题的条件下, 吗? 吗?
AB
AD
=
AC
AD
BD
AD
=
CE
AE
小组活动
如图所示,已知点D为△ ABC的边AB上一点,过点D作直线DE交边AC于点E,要使△ ABC与△ ADE相似,这样的直线有几条?请画出这样的直线,并说明你的理由。
A
B
C
D
E1
E2
E3
E4
问题展示
如果将上述的三角形改为直角三角形,点D为斜边上的已知点,结果又如何?
A
B
C
D
E2
E1
E3
A
B
C
D
E2
E3
E1
如果在右边的直角三角形里,点D改为直角边上的一点,结果又如何呢?
问题展示
无论点D在斜边还是直角边上,
都有3条。
巩固练习
1. 有一个锐角对应相等的两个直角三角形是否相似?为什么?
2.顶角相等的两个等腰三角形是否相似?为什么?
F
A
B
C
D
G
E
3.如下图所示:DE∥FG∥BC,找出图中所有的相似三角形。
答:相似三角形有 △ADE∽△AFG∽△ABC。
到目前为止,相似三角形的识别方法有那些?
方法1:通过定义
方法2:通过两角对应相等。
课 堂 小 结
布置作业:
P75 习题23.2 第2题,第3题(1)
本节课主要学习了哪些内容?你获得了哪些成功体验?
(学生参与评价)
课 堂 评价
A
B
C
D
E
1. 已知D、E分别是△ABC的边AB,AC上的点,若∠A=35°, ∠C=85°,∠AED=60 °则AD·AB= AE·AC
家庭作业
解: ∵ ∠ A= ∠ A ∠ABD=∠C
∴ △ABD ∽ △ACB
∴ AB : AC=AD : AB
∴ AB2 = AD · AC
∵ AD=2 AC=8
∴ AB =4
2. 已知如图, ∠ABD=∠C AD=2 AC=8,求AB
A
B
C
D
家庭作业
我们现在判定两个三角形是否相似,必须要知道它们的对应角是否相等,对应边是否成比例.那么是否存在判定两个三角形相似的简便方法呢?
我们在判断两个三角形全等时,使用了哪些方法?判断三角形相似是否有类似的方法呢?
这两个三角形的三个内角的大小有什么关系?
三个内角对应相等的两个三角形一定相似吗?
三个内角对应相等。
观察你与老师的直角三角尺 ,会相似吗?
(30O 与60O)
相
似
画一个三角形 ,使三个角分别为60°,45°, 75° 。
①同桌分别量出两个三角形三边的长度;
②同桌这两个三角形相似吗?换另三个角试试?
即: 如果一个三角形的三个角分别与另一个三角形的三个角对应相等,那么这两个三角形_______.
相似
一定需三个角吗?
观察
C
A
A'
B
B'
C'
∵ ∠A=∠A', ∠B=∠B'
∴ ΔABC ∽ ΔA'B'C'
用数学符号表示:
相似三角形的识别
相似三角形判定定理1:如果一个三角形的两个角分别与另一个三角形的两个角对应相等,那么这两个三角形相似。 (可简单说成:两角对应相等的两个三角形相似)
例 如图所示,D,E分别是△ABC边AB,AC上的点,DE//BC。
(1) 图中有哪些相等的角?
(2)找出图中的相似三角形,并说明理由;
(3)写出成比例的线段。
例题欣赏
解(1) ∵ DE//BC
∴∠ADE=∠B,∠ADE=∠C
(2) △ADE ∽△ABC .理由是:
∵ ∠ADE=∠B,∠AED=∠C
∴△ADE ∽△ABC
A
E
B
C
D
例 如图所示,D,E分别是△ABC边AB,AC上的点,DE//BC。
(1) 图中有哪些相等的角?
(2)找出图中的相似三角形,并说明理由;
(3)写出成比例的线段。
例题欣赏
解 (3) ∵ △ADE ∽△ABC
A
E
B
C
D
∴
AD
AB
=
DE
BC
=
AE
AC
.
例题欣赏
解 (3) ∵ △ADE ∽△ABC
A
E
B
C
D
∴
AD
AB
=
DE
BC
=
AE
AC
.
在上面例题的条件下, 吗? 吗?
AB
AD
=
AC
AD
BD
AD
=
CE
AE
小组活动
如图所示,已知点D为△ ABC的边AB上一点,过点D作直线DE交边AC于点E,要使△ ABC与△ ADE相似,这样的直线有几条?请画出这样的直线,并说明你的理由。
A
B
C
D
E1
E2
E3
E4
问题展示
如果将上述的三角形改为直角三角形,点D为斜边上的已知点,结果又如何?
A
B
C
D
E2
E1
E3
A
B
C
D
E2
E3
E1
如果在右边的直角三角形里,点D改为直角边上的一点,结果又如何呢?
问题展示
无论点D在斜边还是直角边上,
都有3条。
巩固练习
1. 有一个锐角对应相等的两个直角三角形是否相似?为什么?
2.顶角相等的两个等腰三角形是否相似?为什么?
F
A
B
C
D
G
E
3.如下图所示:DE∥FG∥BC,找出图中所有的相似三角形。
答:相似三角形有 △ADE∽△AFG∽△ABC。
到目前为止,相似三角形的识别方法有那些?
方法1:通过定义
方法2:通过两角对应相等。
课 堂 小 结
布置作业:
P75 习题23.2 第2题,第3题(1)
本节课主要学习了哪些内容?你获得了哪些成功体验?
(学生参与评价)
课 堂 评价
A
B
C
D
E
1. 已知D、E分别是△ABC的边AB,AC上的点,若∠A=35°, ∠C=85°,∠AED=60 °则AD·AB= AE·AC
家庭作业
解: ∵ ∠ A= ∠ A ∠ABD=∠C
∴ △ABD ∽ △ACB
∴ AB : AC=AD : AB
∴ AB2 = AD · AC
∵ AD=2 AC=8
∴ AB =4
2. 已知如图, ∠ABD=∠C AD=2 AC=8,求AB
A
B
C
D
家庭作业
