沪教版(上海)初中数学九年级第一学期 24.4 相似三角形的判定方法探究 课件(共35张ppt)
文档属性
| 名称 | 沪教版(上海)初中数学九年级第一学期 24.4 相似三角形的判定方法探究 课件(共35张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 826.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 00:00:00 | ||
图片预览







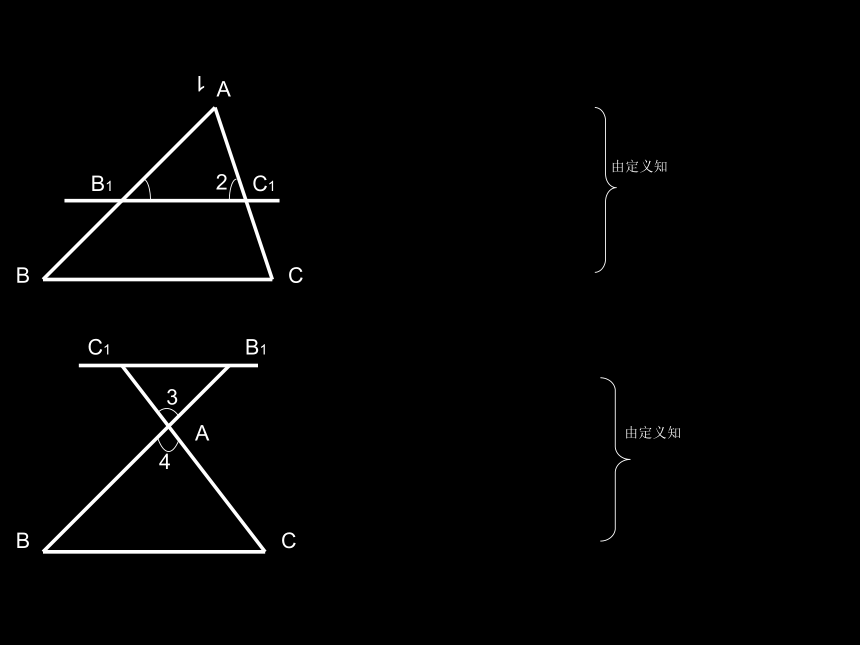




文档简介
(共35张PPT)
教学目标:
通过学习 掌握相似三角形的判定定理;
从定义出发,探究相似三角形的判定方法;
培养合作交流的意识品质。
教学重点:
探究三角形相似的判定方法
复习:
三角形相似的定义
如果一个三角形的三个角与另一个三角
形的三个角对应相等,且他们的三边对
应成比例,那么这两个三角形叫做相似
三角形。
复习:
三角形相似的传递性
如果两个三角形分别与同一个三角形
相似,那么这两个三角形也相似。
复习:
三角形一边的平行线性质定理推论
平行于三角形一边的直线截
其他两边所在的直线,截得的三
角形的三边与原三角形的三边对
应成比例。
C1
1
2
A
B
C
B1
A
B
C
B1
C1
3
4
由定义知
由定义知
相似三角形的预备定理:
平行于三角形一边的直线截其他两边所在的直线,截得的三角形与原三角形相似。
思考探究:
判定两个三角形相似是否必须验证所有的边成比例,所有的对应角相等呢?
如果不需要验证全部条件,那么应该验证多少条件呢?
原则:
用最少的条件来取得两个三角形相似
有两个角对应相等的两个三角形是否相似呢?
有一个角(夹角)对应相等,角的两边对应成比例的两个三角形是否相似呢?
有一个角(非夹角)对应相等,两边对应成比例的两个三角形是否相似呢?
两条边对应成比例的
两个三角形是否相似?
三边对应成比例的两个三角形是否相似?
两边对应成比例,有一个夹角相等的两个三角形是否相似?
两边对应成比例,有一个非夹角相等的两个三角形是否相似?
角
边
能否用来判
定两⊿相似
两边对应成比例
(2)二个角对应相等
角的两边对应成比例
两边对应成比例
(4)一个角(夹角)对应相等
(5)一个角(非夹角)对应相等
三边对应成比例
直角三角形
非直角三角形
(5)
(7)
(3)一个角对应相等
A
B
C
A1
B1
C1
B2
C2
1
2
A
B
C
A1
B1
C1
B2
C2
1
2
已知:
A
B
C
A1
B1
C1
与 不相似
A
B
C
A1
B1
C1
B2
C2
A
B
C
A1
B1
C1
B2
C2
反例:
A
A1
B
C
B1
C1
与 不相似
C2
与 相似
反例:设AB=A1B1,BC=B1C1
A
B
C
A1
B1
C1
与 不相似
A
A1
B1
C1
B2
C2
B
C
判定定理1:
两角对应相等,两个三角形相似
A
B
C
A1
B1
C1
判定定理2:
两边对应成比例且夹角相等,两个三角形相似
A
B
C
A1
B1
C1
判定定理3:
三边对应成比例,两个三角形相似
A
B
C
A1
B1
C1
训练一:
根据下列条件能否判定△ABC和△DEF是否相似?
∠A= ∠D=70°, ∠B=60°, ∠E=50°;
∠A=45°, AB=12,AC=15,
∠D=45°,DE=16,DF=20;
3. AB=2,BC=3,CA=4,
DE=10,EF=15,FD=20;
4.∠A=40°, ∠B=80°, ∠E=80°, ∠F=60°;
5. ∠A=45°, AB=12,AC=15,
∠E=45°,ED=20,EF=16;
6. AB=1,BC=2,CA=1.5,
DE=6,EF=4,FD=8;
7. ∠A=45°, AB=12,AC=15,
∠D=45°,ED=16,EF=20.
例题1 已知:D、E分别是△ABC的边AB、AC上
的点,且∠AED=∠B.
求证:AE·AC=AD·AB
证明:在△AED与△ABC中
∠1=∠B, ∠A=∠A
∴ △AED∽△ABC
即AE·AC=AD·AB
A
B
C
D
E
1
例题2 已知:四边形ABCD的对角线AC与BD相交于
点O,OA=1,OB=1.5,OC=3,OD=2.
求证:(1)△OAD与△OBC是相似三角形.
(2)∠DAO=∠OBC
证明:(1)
O
A
B
C
D
1
2
1.5
3
OA=1,OB=1.5,
OC=3,OD=2.
(2) △OAD∽△OBC ∠DAO=∠OBC
例题3 已知:D、E、F分别是△ABC的边BC、CA、AB
的中点.
求证:△DEF ~△ABC
A
B
C
D
E
F
例题4 已知:在四边形中,∠BAC=∠ADC=90°,
求证:DC⊥BC
A
B
C
D
b
小结:
这节课你学会了什么……
教学目标:
通过学习 掌握相似三角形的判定定理;
从定义出发,探究相似三角形的判定方法;
培养合作交流的意识品质。
教学重点:
探究三角形相似的判定方法
复习:
三角形相似的定义
如果一个三角形的三个角与另一个三角
形的三个角对应相等,且他们的三边对
应成比例,那么这两个三角形叫做相似
三角形。
复习:
三角形相似的传递性
如果两个三角形分别与同一个三角形
相似,那么这两个三角形也相似。
复习:
三角形一边的平行线性质定理推论
平行于三角形一边的直线截
其他两边所在的直线,截得的三
角形的三边与原三角形的三边对
应成比例。
C1
1
2
A
B
C
B1
A
B
C
B1
C1
3
4
由定义知
由定义知
相似三角形的预备定理:
平行于三角形一边的直线截其他两边所在的直线,截得的三角形与原三角形相似。
思考探究:
判定两个三角形相似是否必须验证所有的边成比例,所有的对应角相等呢?
如果不需要验证全部条件,那么应该验证多少条件呢?
原则:
用最少的条件来取得两个三角形相似
有两个角对应相等的两个三角形是否相似呢?
有一个角(夹角)对应相等,角的两边对应成比例的两个三角形是否相似呢?
有一个角(非夹角)对应相等,两边对应成比例的两个三角形是否相似呢?
两条边对应成比例的
两个三角形是否相似?
三边对应成比例的两个三角形是否相似?
两边对应成比例,有一个夹角相等的两个三角形是否相似?
两边对应成比例,有一个非夹角相等的两个三角形是否相似?
角
边
能否用来判
定两⊿相似
两边对应成比例
(2)二个角对应相等
角的两边对应成比例
两边对应成比例
(4)一个角(夹角)对应相等
(5)一个角(非夹角)对应相等
三边对应成比例
直角三角形
非直角三角形
(5)
(7)
(3)一个角对应相等
A
B
C
A1
B1
C1
B2
C2
1
2
A
B
C
A1
B1
C1
B2
C2
1
2
已知:
A
B
C
A1
B1
C1
与 不相似
A
B
C
A1
B1
C1
B2
C2
A
B
C
A1
B1
C1
B2
C2
反例:
A
A1
B
C
B1
C1
与 不相似
C2
与 相似
反例:设AB=A1B1,BC=B1C1
A
B
C
A1
B1
C1
与 不相似
A
A1
B1
C1
B2
C2
B
C
判定定理1:
两角对应相等,两个三角形相似
A
B
C
A1
B1
C1
判定定理2:
两边对应成比例且夹角相等,两个三角形相似
A
B
C
A1
B1
C1
判定定理3:
三边对应成比例,两个三角形相似
A
B
C
A1
B1
C1
训练一:
根据下列条件能否判定△ABC和△DEF是否相似?
∠A= ∠D=70°, ∠B=60°, ∠E=50°;
∠A=45°, AB=12,AC=15,
∠D=45°,DE=16,DF=20;
3. AB=2,BC=3,CA=4,
DE=10,EF=15,FD=20;
4.∠A=40°, ∠B=80°, ∠E=80°, ∠F=60°;
5. ∠A=45°, AB=12,AC=15,
∠E=45°,ED=20,EF=16;
6. AB=1,BC=2,CA=1.5,
DE=6,EF=4,FD=8;
7. ∠A=45°, AB=12,AC=15,
∠D=45°,ED=16,EF=20.
例题1 已知:D、E分别是△ABC的边AB、AC上
的点,且∠AED=∠B.
求证:AE·AC=AD·AB
证明:在△AED与△ABC中
∠1=∠B, ∠A=∠A
∴ △AED∽△ABC
即AE·AC=AD·AB
A
B
C
D
E
1
例题2 已知:四边形ABCD的对角线AC与BD相交于
点O,OA=1,OB=1.5,OC=3,OD=2.
求证:(1)△OAD与△OBC是相似三角形.
(2)∠DAO=∠OBC
证明:(1)
O
A
B
C
D
1
2
1.5
3
OA=1,OB=1.5,
OC=3,OD=2.
(2) △OAD∽△OBC ∠DAO=∠OBC
例题3 已知:D、E、F分别是△ABC的边BC、CA、AB
的中点.
求证:△DEF ~△ABC
A
B
C
D
E
F
例题4 已知:在四边形中,∠BAC=∠ADC=90°,
求证:DC⊥BC
A
B
C
D
b
小结:
这节课你学会了什么……
