沪教版(上海)初中数学九年级第一学期 25.1 锐角三角比的意义 课件(共23张ppt)
文档属性
| 名称 | 沪教版(上海)初中数学九年级第一学期 25.1 锐角三角比的意义 课件(共23张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 00:00:00 | ||
图片预览





文档简介
25.1 锐角的三角比的意义
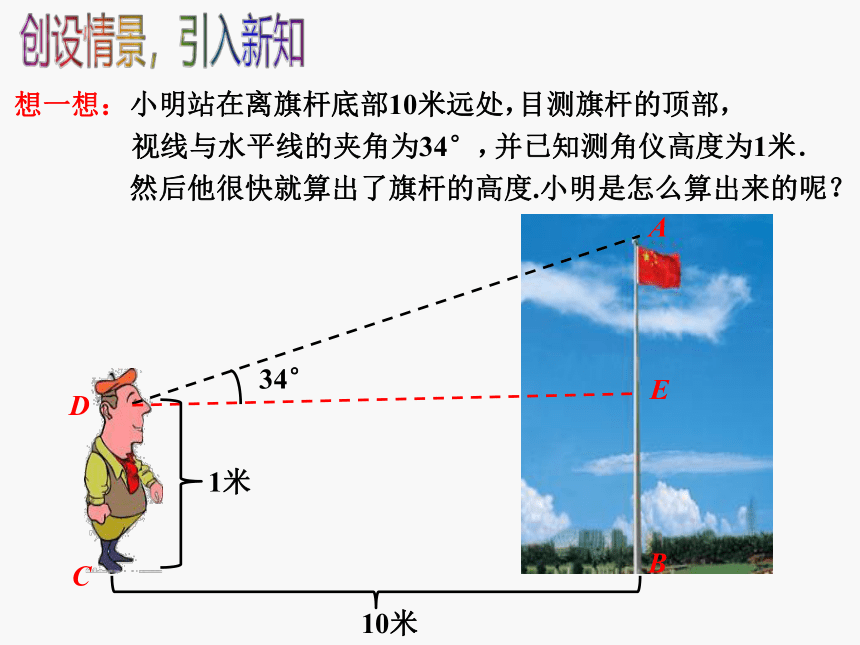
想一想:
小明站在离旗杆底部10米远处,
视线与水平线的夹角为34°,
并已知测角仪高度为1米.
然后他很快就算出了旗杆的高度.小明是怎么算出来的呢?
10米
目测旗杆的顶部,
34°
1米
A
B
C
D
E
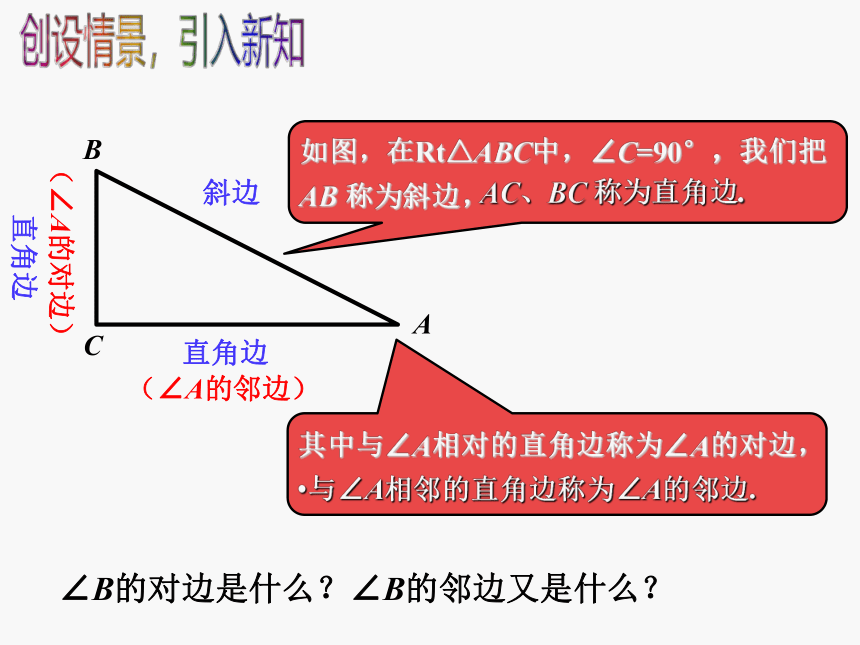
其中与∠A相对的直角边称为∠A的对边,
斜边
直角边
如图,在Rt△ABC中,∠C=90°,我们把AB 称为斜边,
与∠A相邻的直角边称为∠A的邻边.
(∠A的邻边)
直角边
(∠A的对边)
∠B的对边是什么?∠B的邻边又是什么?
AC、BC 称为直角边.
B
C
A
练一练:
如图,在△ABC中,∠ACB=90°.
⑴在Rt△ABC中,∠A的对边是_____, ∠A 的邻边是_____.
BC
AC
CD
AD
ABC
BCD
CD
BD
C
A
B
作CD⊥AB, 垂足为点D.
⑵在Rt△ACD中,∠A的对边是_____ , ∠A 的邻边是_____.
⑶在Rt△_____中,∠B的对边是AC,在Rt△_____中,∠B的邻边是BD.
(4)∠ACD的邻边是_____ ,
∠BCD的对边是_____.
D
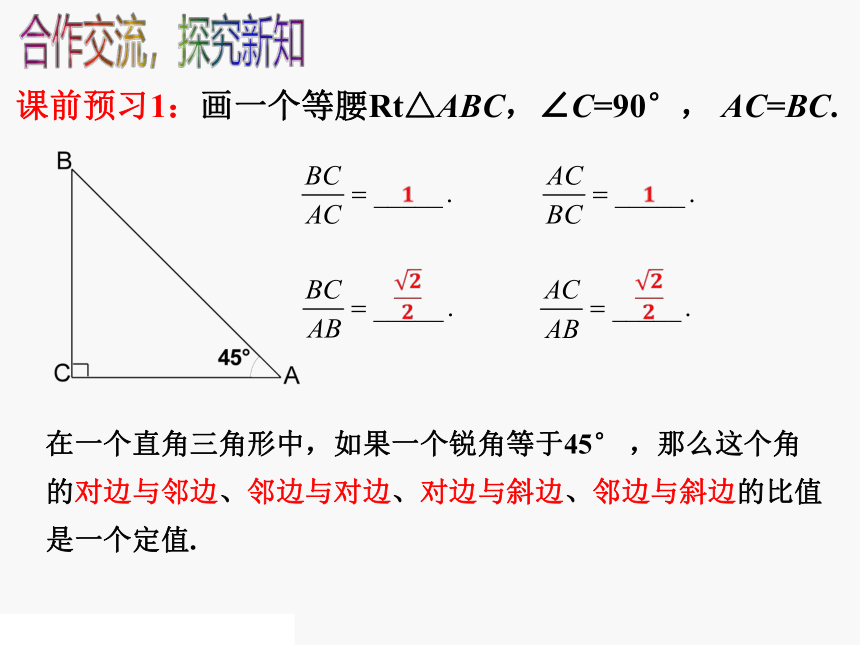
课前预习1:画一个等腰Rt△ABC,∠C=90°, AC=BC.
在一个直角三角形中,如果一个锐角等于45° ,那么这个角的对边与邻边、邻边与对边、对边与斜边、邻边与斜边的比值是一个定值.
课前预习2:画一个Rt△ABC,∠C=90°,∠A=30°.
在一个直角三角形中,如果一个锐角等于30°,那么这个角的
对边与邻边、邻边与对边、对边与斜边、邻边与斜边的比值仍是一个定值.
思考1:在一个直角三角形中,如果给定一个锐角的大小,那么它的对边与邻边的比值是否还是一个确定的值呢?为什么?
思考1:在一个直角三角形中,如果给定一个锐角的大小,那么它的对边与邻边的比值是否还是一个确定的值呢?为什么?
∵∠A是公共角,∠AC1B1=∠AC2B2=90°,
∴△AC1B1∽△AC2B2.
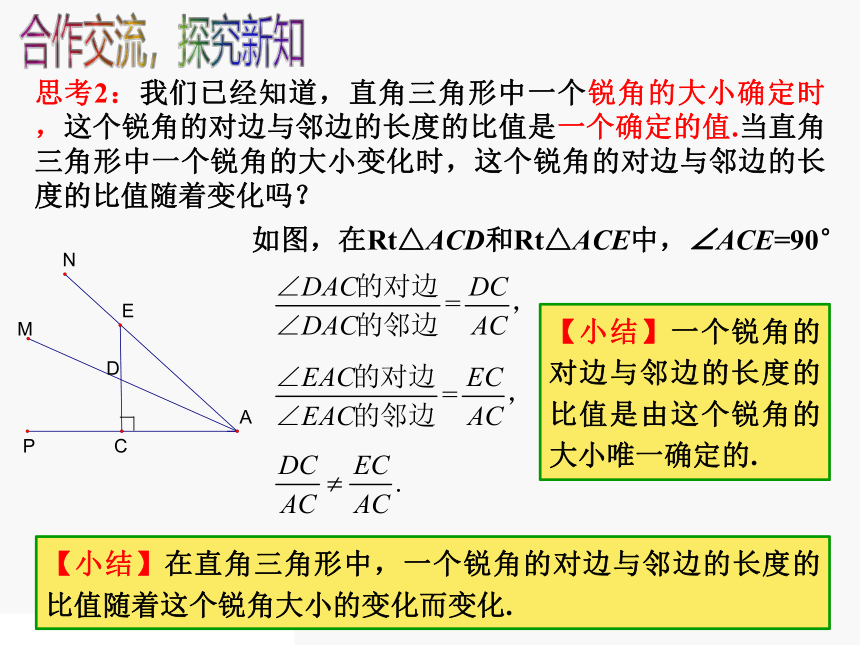
思考2:我们已经知道,直角三角形中一个锐角的大小确定时,这个锐角的对边与邻边的长度的比值是一个确定的值.当直角三角形中一个锐角的大小变化时,这个锐角的对边与邻边的长度的比值随着变化吗?
如图,在Rt△ACD和Rt△ACE中,∠ACE=90°
【小结】在直角三角形中,一个锐角的对边与邻边的长度的比值随着这个锐角大小的变化而变化.
【小结】一个锐角的对边与邻边的长度的比值是由这个锐角的大小唯一确定的.
【小结】如果给定直角三角形的一个锐角的大小,那么这个锐角的对边与邻边的比值就是一个定值.
我们把直角三角形中一个锐角的对边与邻边的比叫做这个锐角的正切(tangent).锐角A的正切记作tanA.
那么∠A的邻边AC与对边BC与的比值是定值吗?
锐角B的正切应如何表示?
【小结】如果给定直角三角形的一个锐角的大小,那么这个锐角的对边与邻边的比值就是一个确定的值.
我们把直角三角形中一个锐角的邻边与对边的比叫做这个锐角的余切(cotangent).锐角A的余切记作cotA.
锐角B的余切应如何表示?
讨论:∠A与∠B的正切和余切的值有什么特点?
讨论:∠A与∠B的正切和余切的值有什么特点?
【小结】在Rt△ABC中,∠C =90°,则有
∠A与∠B的正切与余切都是正实数,为什么?
思考3:在一个直角三角形中,如果给定一个锐角的大小,那么它的对边与斜边的比值、邻边与斜边的比值是否仍是一个确定的值?为什么?
∵∠A是公共角,∠AC1B1=∠AC2B2=90°,
∴△AC1B1∽△AC2B2.
( )
【小结】如果给定直角三角形的一个锐角的大小,那么这个锐角的对边与邻边的比值、邻边与斜边的比值就是一个确定的值.
我们把直角三角形中一个锐角的对边与斜边的比叫做这个锐角的正弦(sine).锐角A的正弦记作sinA.
锐角B的正弦应如何表示?
【小结】如果给定直角三角形的一个锐角的大小,那么这个锐角的对边与邻边的比值、邻边与斜边的比值就是一个确定的值.
我们把直角三角形中一个锐角的邻边与斜边的比叫做这个锐角的余弦(cosine).锐角A的余弦记作cosA.
锐角B的余弦应如何表示?
锐角的三角比:一个锐角的
正切、余切、正弦、余弦
统称为这个
锐角的三角比
讨论:∠A与∠B的正弦和余弦的值有什么特点?
讨论:∠A与∠B的正弦和余弦的值有什么特点?
【小结】在Rt△ABC中,∠C =90°,则有
例题1 在Rt△ABC中,∠C=900,BC=4,AB=5,求∠A的四个三角比的值.
解:在Rt△ABC中,∠C=90°,
∵BC=4,AB=5,
4
5
?
【小结】已知直角三角形的两边,求锐角三角比的步骤:
1.求出直角三角形的各条边;
2.求出相应的锐角三角比.
例题2 在直角坐标平面内有一点P(3,4).
求OP与x轴正半轴的夹角α的四个三角比的值.
解:过点P作PQ⊥x轴,垂足为点Q,
则∠OQP=90°.
由点P的坐标为(3,4),
∴
得OQ=3,QP=4.
Q
4
3
5
当没有直角三角形时,要构造直角三角形来求出锐角三角比的值.
练习 在直角坐标平面内有一点A(-3,-1),点A与原点O
的连线与x轴的负半轴的夹角为α,求α的四个三角比的值.
解:过点A作AQ⊥x轴,垂足为点Q,
Q
则∠OQA=90°.
由点A的坐标为(-3,-1),
得OQ=3,AQ=1.
3
1
α
本节课你学习了什么知识?有什么体会?
谢 谢
想一想:
小明站在离旗杆底部10米远处,
视线与水平线的夹角为34°,
并已知测角仪高度为1米.
然后他很快就算出了旗杆的高度.小明是怎么算出来的呢?
10米
目测旗杆的顶部,
34°
1米
A
B
C
D
E
其中与∠A相对的直角边称为∠A的对边,
斜边
直角边
如图,在Rt△ABC中,∠C=90°,我们把AB 称为斜边,
与∠A相邻的直角边称为∠A的邻边.
(∠A的邻边)
直角边
(∠A的对边)
∠B的对边是什么?∠B的邻边又是什么?
AC、BC 称为直角边.
B
C
A
练一练:
如图,在△ABC中,∠ACB=90°.
⑴在Rt△ABC中,∠A的对边是_____, ∠A 的邻边是_____.
BC
AC
CD
AD
ABC
BCD
CD
BD
C
A
B
作CD⊥AB, 垂足为点D.
⑵在Rt△ACD中,∠A的对边是_____ , ∠A 的邻边是_____.
⑶在Rt△_____中,∠B的对边是AC,在Rt△_____中,∠B的邻边是BD.
(4)∠ACD的邻边是_____ ,
∠BCD的对边是_____.
D
课前预习1:画一个等腰Rt△ABC,∠C=90°, AC=BC.
在一个直角三角形中,如果一个锐角等于45° ,那么这个角的对边与邻边、邻边与对边、对边与斜边、邻边与斜边的比值是一个定值.
课前预习2:画一个Rt△ABC,∠C=90°,∠A=30°.
在一个直角三角形中,如果一个锐角等于30°,那么这个角的
对边与邻边、邻边与对边、对边与斜边、邻边与斜边的比值仍是一个定值.
思考1:在一个直角三角形中,如果给定一个锐角的大小,那么它的对边与邻边的比值是否还是一个确定的值呢?为什么?
思考1:在一个直角三角形中,如果给定一个锐角的大小,那么它的对边与邻边的比值是否还是一个确定的值呢?为什么?
∵∠A是公共角,∠AC1B1=∠AC2B2=90°,
∴△AC1B1∽△AC2B2.
思考2:我们已经知道,直角三角形中一个锐角的大小确定时,这个锐角的对边与邻边的长度的比值是一个确定的值.当直角三角形中一个锐角的大小变化时,这个锐角的对边与邻边的长度的比值随着变化吗?
如图,在Rt△ACD和Rt△ACE中,∠ACE=90°
【小结】在直角三角形中,一个锐角的对边与邻边的长度的比值随着这个锐角大小的变化而变化.
【小结】一个锐角的对边与邻边的长度的比值是由这个锐角的大小唯一确定的.
【小结】如果给定直角三角形的一个锐角的大小,那么这个锐角的对边与邻边的比值就是一个定值.
我们把直角三角形中一个锐角的对边与邻边的比叫做这个锐角的正切(tangent).锐角A的正切记作tanA.
那么∠A的邻边AC与对边BC与的比值是定值吗?
锐角B的正切应如何表示?
【小结】如果给定直角三角形的一个锐角的大小,那么这个锐角的对边与邻边的比值就是一个确定的值.
我们把直角三角形中一个锐角的邻边与对边的比叫做这个锐角的余切(cotangent).锐角A的余切记作cotA.
锐角B的余切应如何表示?
讨论:∠A与∠B的正切和余切的值有什么特点?
讨论:∠A与∠B的正切和余切的值有什么特点?
【小结】在Rt△ABC中,∠C =90°,则有
∠A与∠B的正切与余切都是正实数,为什么?
思考3:在一个直角三角形中,如果给定一个锐角的大小,那么它的对边与斜边的比值、邻边与斜边的比值是否仍是一个确定的值?为什么?
∵∠A是公共角,∠AC1B1=∠AC2B2=90°,
∴△AC1B1∽△AC2B2.
( )
【小结】如果给定直角三角形的一个锐角的大小,那么这个锐角的对边与邻边的比值、邻边与斜边的比值就是一个确定的值.
我们把直角三角形中一个锐角的对边与斜边的比叫做这个锐角的正弦(sine).锐角A的正弦记作sinA.
锐角B的正弦应如何表示?
【小结】如果给定直角三角形的一个锐角的大小,那么这个锐角的对边与邻边的比值、邻边与斜边的比值就是一个确定的值.
我们把直角三角形中一个锐角的邻边与斜边的比叫做这个锐角的余弦(cosine).锐角A的余弦记作cosA.
锐角B的余弦应如何表示?
锐角的三角比:一个锐角的
正切、余切、正弦、余弦
统称为这个
锐角的三角比
讨论:∠A与∠B的正弦和余弦的值有什么特点?
讨论:∠A与∠B的正弦和余弦的值有什么特点?
【小结】在Rt△ABC中,∠C =90°,则有
例题1 在Rt△ABC中,∠C=900,BC=4,AB=5,求∠A的四个三角比的值.
解:在Rt△ABC中,∠C=90°,
∵BC=4,AB=5,
4
5
?
【小结】已知直角三角形的两边,求锐角三角比的步骤:
1.求出直角三角形的各条边;
2.求出相应的锐角三角比.
例题2 在直角坐标平面内有一点P(3,4).
求OP与x轴正半轴的夹角α的四个三角比的值.
解:过点P作PQ⊥x轴,垂足为点Q,
则∠OQP=90°.
由点P的坐标为(3,4),
∴
得OQ=3,QP=4.
Q
4
3
5
当没有直角三角形时,要构造直角三角形来求出锐角三角比的值.
练习 在直角坐标平面内有一点A(-3,-1),点A与原点O
的连线与x轴的负半轴的夹角为α,求α的四个三角比的值.
解:过点A作AQ⊥x轴,垂足为点Q,
Q
则∠OQA=90°.
由点A的坐标为(-3,-1),
得OQ=3,AQ=1.
3
1
α
本节课你学习了什么知识?有什么体会?
谢 谢
