沪教版(上海)初中数学九年级第一学期 25.4 几何应用问题 课件(共14张ppt)
文档属性
| 名称 | 沪教版(上海)初中数学九年级第一学期 25.4 几何应用问题 课件(共14张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 859.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 17:43:08 | ||
图片预览



文档简介
几何应用问题
几何应用问题:
是利用几何知识解决生活实际中的数学问题。几何应用问题是一个考点,也是一个难点。
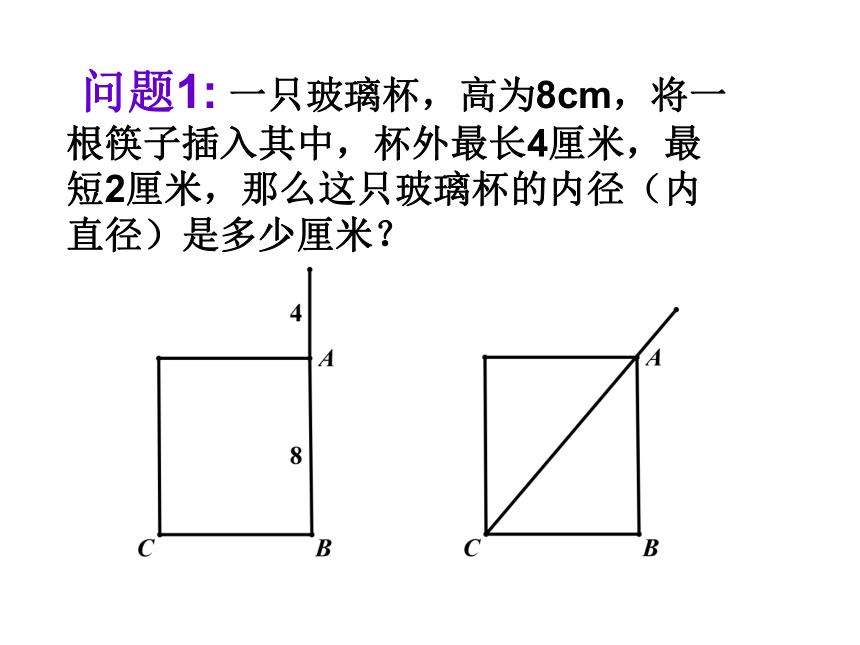
问题1: 一只玻璃杯,高为8cm,将一根筷子插入其中,杯外最长4厘米,最短2厘米,那么这只玻璃杯的内径(内直径)是多少厘米?
问题1: 一只玻璃杯,高为8cm,将一根筷子插入其中,杯外最长4厘米,最短2厘米,那么这只玻璃杯的内径(内直径)是多少厘米?
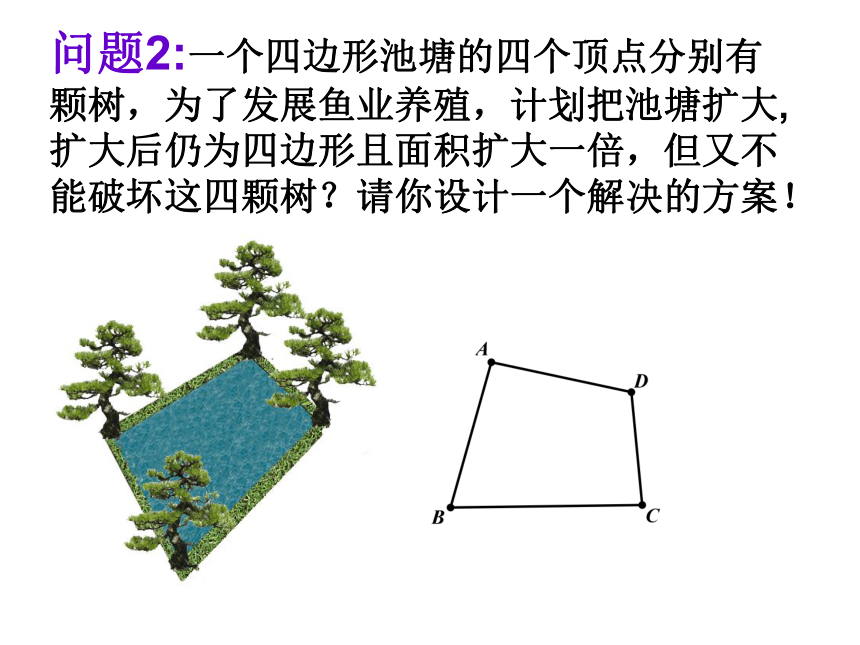
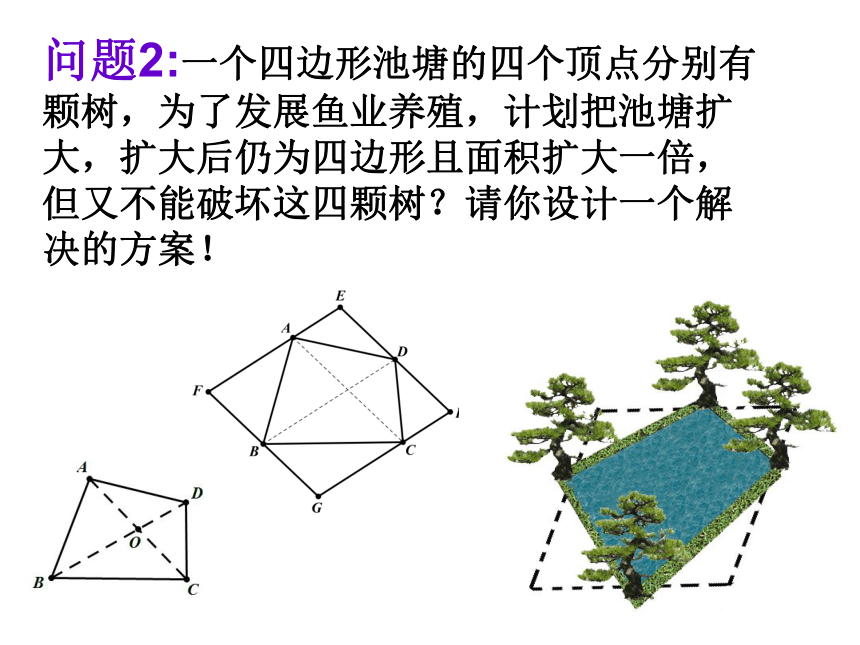
问题2:一个四边形池塘的四个顶点分别有颗树,为了发展鱼业养殖,计划把池塘扩大,扩大后仍为四边形且面积扩大一倍,但又不能破坏这四颗树?请你设计一个解决的方案!
问题2:一个四边形池塘的四个顶点分别有颗树,为了发展鱼业养殖,计划把池塘扩大,扩大后仍为四边形且面积扩大一倍,但又不能破坏这四颗树?请你设计一个解决的方案!
读懂题目
画出图形(建立数学模型)
运用所学数学知识解决问题
是否符合实际意义后作答
解题的一般步骤:
一块三角形的绿地,三边的长分别为120m , 60 m ,80m, 为了方便居民,也为了美观,准备在绿地中间经过同一点修三条长一样(宽忽略不计)且都与三角形一边平行的三条小道,该如何选点施工?
例1
一块三角形的绿地,三边的长为分别为120m , 60 m ,80m, 为了方便居民,也为了美观,准备在绿地中间经过同一点修三条长一样(宽忽略不计)且都与三角形一边平行的三条小道,该如何选点施工?
例1
例2
某圆拱形拉索桥底部水平距离64米,桥拱
最高点到桥面的高度是16米,桥面每隔4米
有一根钢丝拉索,(1)求圆拱桥的半径
(2)求左端第二根拉索的长度
例2
某圆拱形拉索桥底部水平距离64米,桥拱
最高点到桥面的高度是16米,桥面每隔4米
有一根钢丝拉索,(1)求圆拱桥的半径
(2)求左端第二根拉索的长度
例2
某圆拱形拉索桥底部水平距离64米,桥拱
最高点到桥面的高度是16米,桥面每隔4米
有一根钢丝拉索,(1)求圆拱桥的半径
(2)求左端第二根拉索的长度
例2
某圆拱形拉索桥底部水平距离64米,桥拱
最高点到桥面的高度是16米,桥面每隔4米
有一根钢丝拉索,(1)求圆拱桥的半径
(2)求左端第二根拉索的长度
小结:
1 、解几何应用问题的一般步骤
2、解几何应用问题中的常见的数学思想
几何应用问题:
是利用几何知识解决生活实际中的数学问题。几何应用问题是一个考点,也是一个难点。
问题1: 一只玻璃杯,高为8cm,将一根筷子插入其中,杯外最长4厘米,最短2厘米,那么这只玻璃杯的内径(内直径)是多少厘米?
问题1: 一只玻璃杯,高为8cm,将一根筷子插入其中,杯外最长4厘米,最短2厘米,那么这只玻璃杯的内径(内直径)是多少厘米?
问题2:一个四边形池塘的四个顶点分别有颗树,为了发展鱼业养殖,计划把池塘扩大,扩大后仍为四边形且面积扩大一倍,但又不能破坏这四颗树?请你设计一个解决的方案!
问题2:一个四边形池塘的四个顶点分别有颗树,为了发展鱼业养殖,计划把池塘扩大,扩大后仍为四边形且面积扩大一倍,但又不能破坏这四颗树?请你设计一个解决的方案!
读懂题目
画出图形(建立数学模型)
运用所学数学知识解决问题
是否符合实际意义后作答
解题的一般步骤:
一块三角形的绿地,三边的长分别为120m , 60 m ,80m, 为了方便居民,也为了美观,准备在绿地中间经过同一点修三条长一样(宽忽略不计)且都与三角形一边平行的三条小道,该如何选点施工?
例1
一块三角形的绿地,三边的长为分别为120m , 60 m ,80m, 为了方便居民,也为了美观,准备在绿地中间经过同一点修三条长一样(宽忽略不计)且都与三角形一边平行的三条小道,该如何选点施工?
例1
例2
某圆拱形拉索桥底部水平距离64米,桥拱
最高点到桥面的高度是16米,桥面每隔4米
有一根钢丝拉索,(1)求圆拱桥的半径
(2)求左端第二根拉索的长度
例2
某圆拱形拉索桥底部水平距离64米,桥拱
最高点到桥面的高度是16米,桥面每隔4米
有一根钢丝拉索,(1)求圆拱桥的半径
(2)求左端第二根拉索的长度
例2
某圆拱形拉索桥底部水平距离64米,桥拱
最高点到桥面的高度是16米,桥面每隔4米
有一根钢丝拉索,(1)求圆拱桥的半径
(2)求左端第二根拉索的长度
例2
某圆拱形拉索桥底部水平距离64米,桥拱
最高点到桥面的高度是16米,桥面每隔4米
有一根钢丝拉索,(1)求圆拱桥的半径
(2)求左端第二根拉索的长度
小结:
1 、解几何应用问题的一般步骤
2、解几何应用问题中的常见的数学思想
