26.1 二次函数的概念 课件(共18张PPT)
文档属性
| 名称 | 26.1 二次函数的概念 课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 18:44:33 | ||
图片预览





文档简介
26.1 二次函数的概念
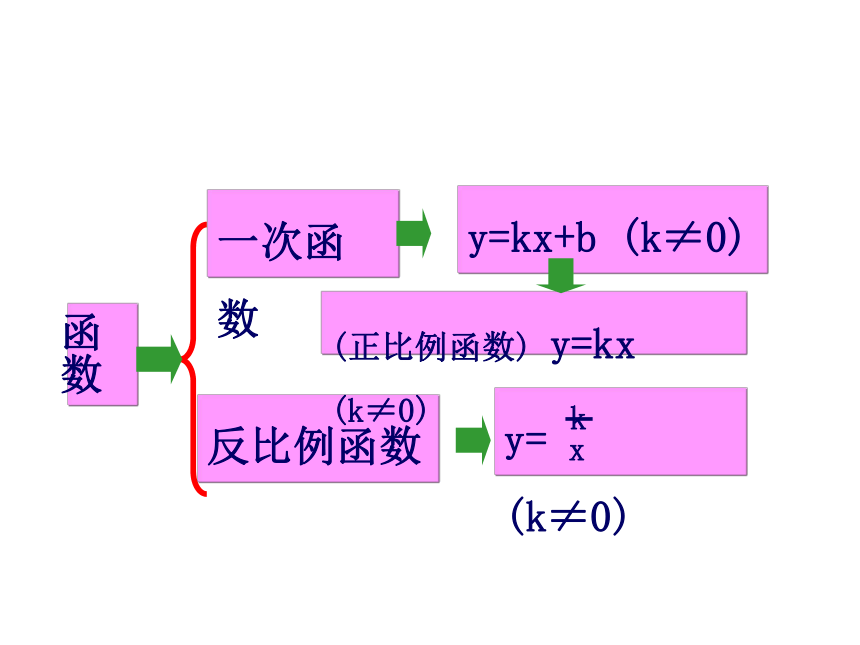
函数
一次函数
反比例函数
y=kx+b (k≠0)
(正比例函数) y=kx (k≠0)
y= (k≠0)
k
x
问题1:
若圆的半径为x厘米,圆的面积为y平方厘米,试写出y关于x的函数解析式.
问题2:
甲、乙两数的和为20,设甲数为x,甲、乙两数的积为y,试写出y关于x的函数解析式.
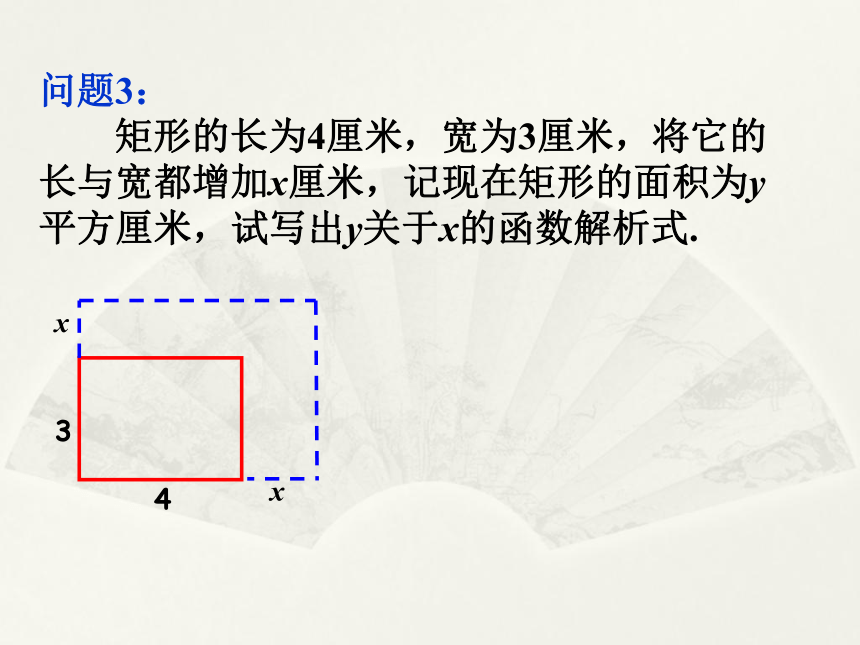
问题3:
矩形的长为4厘米,宽为3厘米,将它的长与宽都增加x厘米,记现在矩形的面积为y平方厘米,试写出y关于x的函数解析式.
x
x
3
4
问题4:
汽车产业是我市支柱产业之一,产量和效益逐年增加. 据统计,2014年我市某种品牌汽车的年产量为6万辆,到2016年,该品牌汽车的年产量达到y万辆. 若该品牌汽车年产量的年增长率从2014年开始保持不变,均为x,试写出y关于x的函数解析式.
定义:
一般地,解析式形如
y=ax?+bx+c (其中a、b、c是常数,且 a≠ 0)
的函数叫做二次函数.
二次函数y=ax?+bx+c 的定义域为一切实数.
遇到实际问题,具体分析。
【思索归纳】
例1. 下列关于x的函数,是不是二次函数?
是
不是
【概念辨析】
不是
是
不是
不是
不是
不是
归纳:( 化为最简式的前提下)
(1)二次函数解析式中,关于x的代数式一定是整式;
(2)整式中自变量的最高次数为二次.
是
【概念辨析】
例2.已知关于 x 的函数
若它是关于x的二次函数,求m的取值范围.
【概念辨析】
例2.已知关于 x 的函数
y=(m2-2m-3)x2+(m+1)x+m2.
(1)若它是关于x的二次函数,
m要满足的条件是 .
(2)若它是关于x的一次函数,
m要满足的条件是 .
一次函数
二次函数
解析式
y=ax?+bx+c (a≠ 0)
y=kx+b (k≠ 0)
例3、如图,用长为20米的篱笆,一面靠墙
(墙长度超过20米),围成一个矩形的花圃.设AB边的长为x米,花圃的面积为 y平方米.
(1)求y关于x的函数解析式及函数的定义域;
x
x
20-2x
B
C
D
A
(2)当x=6时,y的 值是多少?当y=32时,x的值多少?
(3)花圃的面积是否可能等于60平方米?为什么?
墙长度超过20米
(4)若题目的条件修改一下,那么第1.2问还一样吗?
例题4 已知:如图,在Rt△ABC中,∠C=90°,AC=BC=4,点D为边AB上的一个动点(不与A、B两点重合),过点D作DE⊥AC,垂足为点E,联结DC.
(1)设线段AD的长为x,线段EC的长为y,那么y关于x的函数解析式是 ,y是x的 函数.
(2)设线段AE长为x,△ACD的面积为y,那么y关于x的函数关系式是 ,y是x的 函数.
(3)◆设 为x, 为y,那么y关于x 的函数解析式是 ,
y是x的二次函数.
◆设 为x, 为y,
那么y关于x 的函数解析式是 ,
y是x的二次函数.
【课堂小结】
具体函数的定义
(解析式、定义域)
性 质
图 像
两个
变量
实际
问题
二、学习一个具体函数的过程:
一、二次函数的定义
【布置作业】
1、必做题:尝试画函数y=x2 的函数图像。
2、上海作业:选做最后两道
列出函数关系式以及定义域:
1、 把一根长40厘米的铁丝剪成两段,再分别把每一段弯折成一个正方形(不计接头处的损耗).设其中一段铁丝长x厘米,两个正方形的面积和等于y平方厘米,求y关于x的函数解析式.
x
2、扇形的面积S与圆心角、半径的函数关系
式是————
(1)若r为常数,S是n的什么函数?(2)若n为常数,S是r的什么函数?
2. 心理学家研究发现, 在一定的时间范围内,学生对概念的接受程度y与提出概念所用的时间x(分钟)之间满足函数关系式:
y的值越大,表示接受程度越高.
(1)若用10分钟提出概念,学生的接受程度y的值是多少?
(2)如果分别用5分钟、10分钟或20分钟来提出这一概念,
那么三者相比,用哪种方式,学生的接受程度更高?
函数
一次函数
反比例函数
y=kx+b (k≠0)
(正比例函数) y=kx (k≠0)
y= (k≠0)
k
x
问题1:
若圆的半径为x厘米,圆的面积为y平方厘米,试写出y关于x的函数解析式.
问题2:
甲、乙两数的和为20,设甲数为x,甲、乙两数的积为y,试写出y关于x的函数解析式.
问题3:
矩形的长为4厘米,宽为3厘米,将它的长与宽都增加x厘米,记现在矩形的面积为y平方厘米,试写出y关于x的函数解析式.
x
x
3
4
问题4:
汽车产业是我市支柱产业之一,产量和效益逐年增加. 据统计,2014年我市某种品牌汽车的年产量为6万辆,到2016年,该品牌汽车的年产量达到y万辆. 若该品牌汽车年产量的年增长率从2014年开始保持不变,均为x,试写出y关于x的函数解析式.
定义:
一般地,解析式形如
y=ax?+bx+c (其中a、b、c是常数,且 a≠ 0)
的函数叫做二次函数.
二次函数y=ax?+bx+c 的定义域为一切实数.
遇到实际问题,具体分析。
【思索归纳】
例1. 下列关于x的函数,是不是二次函数?
是
不是
【概念辨析】
不是
是
不是
不是
不是
不是
归纳:( 化为最简式的前提下)
(1)二次函数解析式中,关于x的代数式一定是整式;
(2)整式中自变量的最高次数为二次.
是
【概念辨析】
例2.已知关于 x 的函数
若它是关于x的二次函数,求m的取值范围.
【概念辨析】
例2.已知关于 x 的函数
y=(m2-2m-3)x2+(m+1)x+m2.
(1)若它是关于x的二次函数,
m要满足的条件是 .
(2)若它是关于x的一次函数,
m要满足的条件是 .
一次函数
二次函数
解析式
y=ax?+bx+c (a≠ 0)
y=kx+b (k≠ 0)
例3、如图,用长为20米的篱笆,一面靠墙
(墙长度超过20米),围成一个矩形的花圃.设AB边的长为x米,花圃的面积为 y平方米.
(1)求y关于x的函数解析式及函数的定义域;
x
x
20-2x
B
C
D
A
(2)当x=6时,y的 值是多少?当y=32时,x的值多少?
(3)花圃的面积是否可能等于60平方米?为什么?
墙长度超过20米
(4)若题目的条件修改一下,那么第1.2问还一样吗?
例题4 已知:如图,在Rt△ABC中,∠C=90°,AC=BC=4,点D为边AB上的一个动点(不与A、B两点重合),过点D作DE⊥AC,垂足为点E,联结DC.
(1)设线段AD的长为x,线段EC的长为y,那么y关于x的函数解析式是 ,y是x的 函数.
(2)设线段AE长为x,△ACD的面积为y,那么y关于x的函数关系式是 ,y是x的 函数.
(3)◆设 为x, 为y,那么y关于x 的函数解析式是 ,
y是x的二次函数.
◆设 为x, 为y,
那么y关于x 的函数解析式是 ,
y是x的二次函数.
【课堂小结】
具体函数的定义
(解析式、定义域)
性 质
图 像
两个
变量
实际
问题
二、学习一个具体函数的过程:
一、二次函数的定义
【布置作业】
1、必做题:尝试画函数y=x2 的函数图像。
2、上海作业:选做最后两道
列出函数关系式以及定义域:
1、 把一根长40厘米的铁丝剪成两段,再分别把每一段弯折成一个正方形(不计接头处的损耗).设其中一段铁丝长x厘米,两个正方形的面积和等于y平方厘米,求y关于x的函数解析式.
x
2、扇形的面积S与圆心角、半径的函数关系
式是————
(1)若r为常数,S是n的什么函数?(2)若n为常数,S是r的什么函数?
2. 心理学家研究发现, 在一定的时间范围内,学生对概念的接受程度y与提出概念所用的时间x(分钟)之间满足函数关系式:
y的值越大,表示接受程度越高.
(1)若用10分钟提出概念,学生的接受程度y的值是多少?
(2)如果分别用5分钟、10分钟或20分钟来提出这一概念,
那么三者相比,用哪种方式,学生的接受程度更高?
