第26章小结 二次函数的复习 课件(共22张PPT)
文档属性
| 名称 | 第26章小结 二次函数的复习 课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 00:00:00 | ||
图片预览






文档简介
知识点回顾一:
1、什么样的函数是二次函数?它的定义域是怎样的?
二次函数的定义域一般为一切实数.
形如 的函数叫二次函数.
实际问题中二次函数的定义域由实际情况决定.
二次函数的概念及定义域
1、若函数 为二次函数,那么 m = .
2、已知三角形一边的长为 x ,这边上的高比这边长1 ,设此三角
形的面积为 y ,那么 y 与 x 的关系式为 ,
自变量x的取值范围为 .
2、从特殊到一般,我们学过哪几种类型的二次函数?
写出它们的表达式.
学习函数,主要是要研究函数图象与性质,
研究了二次函数的开口方向、顶点坐标、对称轴、
y 随 x 变化情况的一些性质.
那么,我们研究了二次函数图象的哪些性质呢?
抛物线
开口方向
顶点坐标
对称轴
顶点位置
大致图象
函数变化
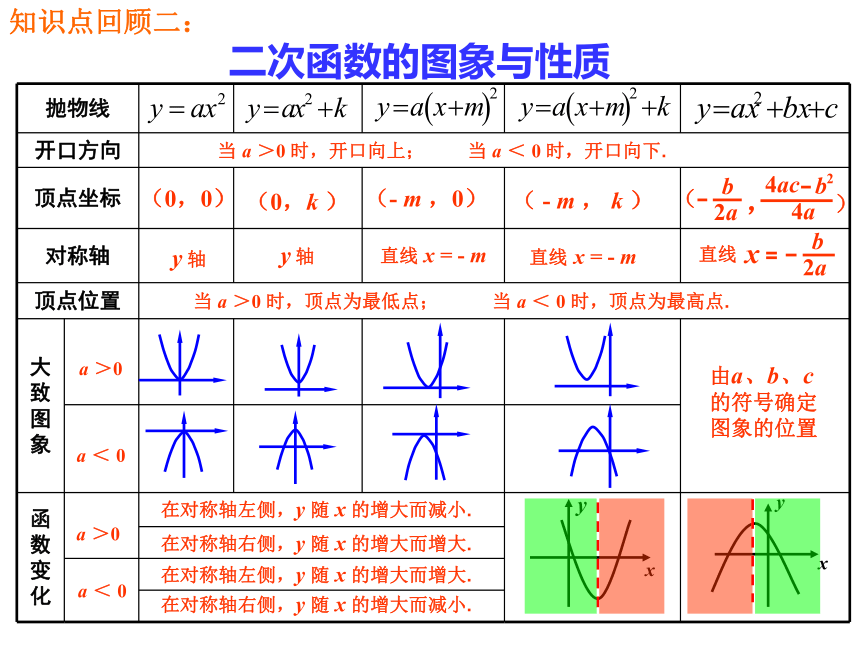
当 a >0 时,开口向上; 当 a < 0 时,开口向下.
b
2a
2
b
4a
4ac
(
,
(
( - m , k )
(- m ,0)
(0,k )
(0,0)
直线 x = - m
直线 x = - m
y 轴
当 a >0 时,顶点为最低点; 当 a < 0 时,顶点为最高点.
a < 0
a >0
a >0
a < 0
x =
直线
b
2a
y 轴
在对称轴右侧,y 随 x 的增大而减小.
x
y
x
y
在对称轴左侧,y 随 x 的增大而增大.
在对称轴右侧,y 随 x 的增大而增大.
在对称轴左侧,y 随 x 的增大而减小.
由a、b、c的符号确定图象的位置
知识点回顾二:
二次函数的图象与性质
4、当a 时,抛物线 y =(a +2)x 2 的顶点为最高点.
2、抛物线 y = 3x 2 + 2 的开口向 , 顶点坐标为 .
1、当 m 时,抛物线 y =(m 1)x 2 的开口向上.
3、抛物线 y =2( x +1)2 - 4 的顶点坐标为
对称轴为 .
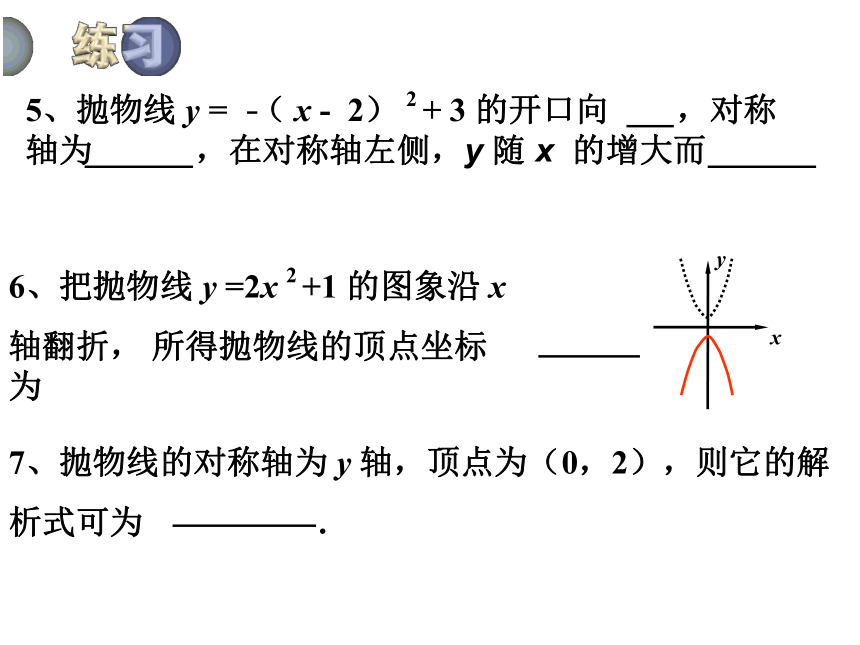
7、抛物线的对称轴为 y 轴,顶点为(0,2),则它的解
析式可为 .
6、把抛物线 y =2x 2 +1 的图象沿 x
轴翻折, 所得抛物线的顶点坐标为
5、抛物线 y = ( x - 2) 2 + 3 的开口向 ,对称轴为 ,在对称轴左侧,y 随 x 的增大而
x
y
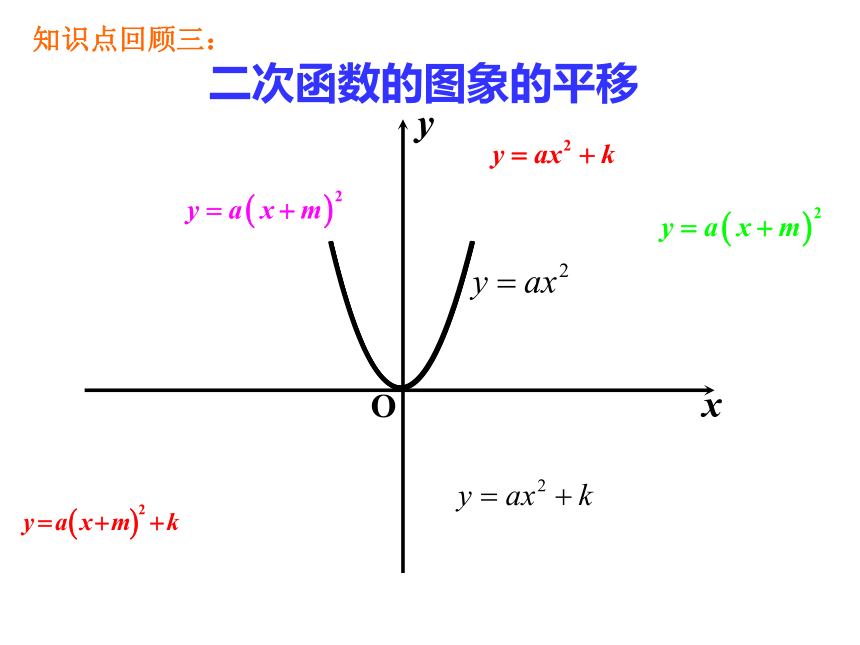
知识点回顾三:
二次函数的图象的平移
O
x
y
二次函数图象平移规律
顶点式中看平移,
上下左右看仔细.
左加右减自变量,
上加下减常数项.
1、将抛物线 y = 2x 2 向上平移2个单位,所得抛物线的解析式为 .
2、将抛物线 y = 3x 2 1向上平移3个单位,所得抛物线
的解析式为 . 抛物线的顶点由 变 为 .
3、抛物线 y = x 2 4 的图象可以看成是把函数 y = x 2 的图象向 平移 个单位所得,如把这图象向左平移2个单位,得到图象的解析式为 .
思考:
小明在做二次函数的作业时,遇到了这么一道题目:
请问:抛物线 与抛物线 的图象的形状和大小一样吗?为什么?如果是一样的,那么,把第一条抛物线通过怎么样的平移,可以与第二个抛物线的图象重合?
小明的解答:
因为两个抛物线的解析式二次项系数相同,所以这两条抛物线的形状、大小相同,它们只是位置不同。
又因为第一条抛物线与 y 轴交点为(0,1),第二条抛物线与 y 轴的交点为(0,3)所以只要把第一条抛物线向上平移2个单位就可以与第二条抛物线的图象重合。
小明的解答完全正确吗?
9
8
7
6
5
4
3
2
1
-1
-8
-6
-4
-2
2
4
5
8
x
y
-1
-3
-5
-7
1
3
6
7
看看小明的错误在哪里?
y=x2-2x+3
知识点回顾四:
二次函数一般式与顶点式的转化
一般式
顶点式
配 方
展 开
b
2a
2
b
4a
4ac
(
,
(
x =
直线
b
2a
2
y ax bx c
+
+
=
比较可得:
二次函数
的
顶点坐标为:
对称轴为:
顶点坐标:(-m,k)
对称轴:直线x=-m
知识点回顾四:
二次函数一般式与顶点式的转化
例题:
把抛物线 化为 形式,并指出它的开口方向、顶点坐标、对称轴以及 y 随
x 的变化情况.
把抛物线 化为 的形式,并指出它的开口方向、顶点坐标、对称轴以及 y 随 x 的变化情况.
知识点回顾五:
待定系数法求二次函数解析式
议一议:
如果一条抛物线过点(1,0)(3,0)(0,3),
你有几种办法求出抛物线的解析式?
抛物线 y=ax2+bx+c 的大致图象与a、b、c 符号的关系
应用一:
例题:
抛物线 y=ax2+bx+c 的大致图象如图所示,试确定a、b、c的符号.
o
y
x
解: ∵ 抛物线开口向上,
∴ a> 0,
∵ 抛物线与 y 轴交于正半轴,
∴ c> 0,
直线
b
2a
∵
>0
b
2a
∴
<0
又∵ a> 0,
∴ b < 0.
抛物线 y =ax2+bx+c如图,试确定a、b、c的符号.
x
y
o
a 0
b 0
c 0
a 0
b 0
c 0
>
>
>
<
<
>
9
8
7
6
5
4
3
2
1
-1
-8
-6
-4
-2
2
4
8
x
y
-1
-3
-5
-7
1
3
7
已知一个二次函数的图像经过点A(1,0),B(3,0)
C(0,3)
求(1)函数解析式.
(2)求顶点D坐标.
应用二:
5
6
A
B
C
D
9
8
7
6
5
4
3
2
1
-1
-8
-6
-4
-2
2
4
5
8
x
y
-1
-3
-5
-7
1
3
6
7
A
B
C
已知一个二次函数的图像经过点A(1,0),B(3,0)
C(0,3)求(3)求∠ACB的正弦值.
应用二:
D
1、本课主要复习了哪些内容?
2、通过复习,你有什么体会或收获呢?
二次函数
1)用配方法求其顶点D的坐标;
2)求其与y轴的交点C的坐标、与x轴交点A、B(且点A在点B的左边)的坐标。
1. 将 图像向右平移2个单位,再向上平移1个单位,可得解析式为 ;
2. 将 图像沿着y轴翻折可得解析式为 ;
3. 将 图像沿着x轴翻折可得解析式为 ;
4. 将 图像绕着顶点旋转180°可得解析式为 ;
该图是函数 的图像,你能结合图中点的坐标找一找图中有哪些特殊的形吗?这些特殊图形之间有什么关系吗?
2. 将图中点O沿着直线BC翻折后得点E,请写出点E的坐标。
1、什么样的函数是二次函数?它的定义域是怎样的?
二次函数的定义域一般为一切实数.
形如 的函数叫二次函数.
实际问题中二次函数的定义域由实际情况决定.
二次函数的概念及定义域
1、若函数 为二次函数,那么 m = .
2、已知三角形一边的长为 x ,这边上的高比这边长1 ,设此三角
形的面积为 y ,那么 y 与 x 的关系式为 ,
自变量x的取值范围为 .
2、从特殊到一般,我们学过哪几种类型的二次函数?
写出它们的表达式.
学习函数,主要是要研究函数图象与性质,
研究了二次函数的开口方向、顶点坐标、对称轴、
y 随 x 变化情况的一些性质.
那么,我们研究了二次函数图象的哪些性质呢?
抛物线
开口方向
顶点坐标
对称轴
顶点位置
大致图象
函数变化
当 a >0 时,开口向上; 当 a < 0 时,开口向下.
b
2a
2
b
4a
4ac
(
,
(
( - m , k )
(- m ,0)
(0,k )
(0,0)
直线 x = - m
直线 x = - m
y 轴
当 a >0 时,顶点为最低点; 当 a < 0 时,顶点为最高点.
a < 0
a >0
a >0
a < 0
x =
直线
b
2a
y 轴
在对称轴右侧,y 随 x 的增大而减小.
x
y
x
y
在对称轴左侧,y 随 x 的增大而增大.
在对称轴右侧,y 随 x 的增大而增大.
在对称轴左侧,y 随 x 的增大而减小.
由a、b、c的符号确定图象的位置
知识点回顾二:
二次函数的图象与性质
4、当a 时,抛物线 y =(a +2)x 2 的顶点为最高点.
2、抛物线 y = 3x 2 + 2 的开口向 , 顶点坐标为 .
1、当 m 时,抛物线 y =(m 1)x 2 的开口向上.
3、抛物线 y =2( x +1)2 - 4 的顶点坐标为
对称轴为 .
7、抛物线的对称轴为 y 轴,顶点为(0,2),则它的解
析式可为 .
6、把抛物线 y =2x 2 +1 的图象沿 x
轴翻折, 所得抛物线的顶点坐标为
5、抛物线 y = ( x - 2) 2 + 3 的开口向 ,对称轴为 ,在对称轴左侧,y 随 x 的增大而
x
y
知识点回顾三:
二次函数的图象的平移
O
x
y
二次函数图象平移规律
顶点式中看平移,
上下左右看仔细.
左加右减自变量,
上加下减常数项.
1、将抛物线 y = 2x 2 向上平移2个单位,所得抛物线的解析式为 .
2、将抛物线 y = 3x 2 1向上平移3个单位,所得抛物线
的解析式为 . 抛物线的顶点由 变 为 .
3、抛物线 y = x 2 4 的图象可以看成是把函数 y = x 2 的图象向 平移 个单位所得,如把这图象向左平移2个单位,得到图象的解析式为 .
思考:
小明在做二次函数的作业时,遇到了这么一道题目:
请问:抛物线 与抛物线 的图象的形状和大小一样吗?为什么?如果是一样的,那么,把第一条抛物线通过怎么样的平移,可以与第二个抛物线的图象重合?
小明的解答:
因为两个抛物线的解析式二次项系数相同,所以这两条抛物线的形状、大小相同,它们只是位置不同。
又因为第一条抛物线与 y 轴交点为(0,1),第二条抛物线与 y 轴的交点为(0,3)所以只要把第一条抛物线向上平移2个单位就可以与第二条抛物线的图象重合。
小明的解答完全正确吗?
9
8
7
6
5
4
3
2
1
-1
-8
-6
-4
-2
2
4
5
8
x
y
-1
-3
-5
-7
1
3
6
7
看看小明的错误在哪里?
y=x2-2x+3
知识点回顾四:
二次函数一般式与顶点式的转化
一般式
顶点式
配 方
展 开
b
2a
2
b
4a
4ac
(
,
(
x =
直线
b
2a
2
y ax bx c
+
+
=
比较可得:
二次函数
的
顶点坐标为:
对称轴为:
顶点坐标:(-m,k)
对称轴:直线x=-m
知识点回顾四:
二次函数一般式与顶点式的转化
例题:
把抛物线 化为 形式,并指出它的开口方向、顶点坐标、对称轴以及 y 随
x 的变化情况.
把抛物线 化为 的形式,并指出它的开口方向、顶点坐标、对称轴以及 y 随 x 的变化情况.
知识点回顾五:
待定系数法求二次函数解析式
议一议:
如果一条抛物线过点(1,0)(3,0)(0,3),
你有几种办法求出抛物线的解析式?
抛物线 y=ax2+bx+c 的大致图象与a、b、c 符号的关系
应用一:
例题:
抛物线 y=ax2+bx+c 的大致图象如图所示,试确定a、b、c的符号.
o
y
x
解: ∵ 抛物线开口向上,
∴ a> 0,
∵ 抛物线与 y 轴交于正半轴,
∴ c> 0,
直线
b
2a
∵
>0
b
2a
∴
<0
又∵ a> 0,
∴ b < 0.
抛物线 y =ax2+bx+c如图,试确定a、b、c的符号.
x
y
o
a 0
b 0
c 0
a 0
b 0
c 0
>
>
>
<
<
>
9
8
7
6
5
4
3
2
1
-1
-8
-6
-4
-2
2
4
8
x
y
-1
-3
-5
-7
1
3
7
已知一个二次函数的图像经过点A(1,0),B(3,0)
C(0,3)
求(1)函数解析式.
(2)求顶点D坐标.
应用二:
5
6
A
B
C
D
9
8
7
6
5
4
3
2
1
-1
-8
-6
-4
-2
2
4
5
8
x
y
-1
-3
-5
-7
1
3
6
7
A
B
C
已知一个二次函数的图像经过点A(1,0),B(3,0)
C(0,3)求(3)求∠ACB的正弦值.
应用二:
D
1、本课主要复习了哪些内容?
2、通过复习,你有什么体会或收获呢?
二次函数
1)用配方法求其顶点D的坐标;
2)求其与y轴的交点C的坐标、与x轴交点A、B(且点A在点B的左边)的坐标。
1. 将 图像向右平移2个单位,再向上平移1个单位,可得解析式为 ;
2. 将 图像沿着y轴翻折可得解析式为 ;
3. 将 图像沿着x轴翻折可得解析式为 ;
4. 将 图像绕着顶点旋转180°可得解析式为 ;
该图是函数 的图像,你能结合图中点的坐标找一找图中有哪些特殊的形吗?这些特殊图形之间有什么关系吗?
2. 将图中点O沿着直线BC翻折后得点E,请写出点E的坐标。
