25.1锐角的三角比的意义(1) 课件(共17张PPT)
文档属性
| 名称 | 25.1锐角的三角比的意义(1) 课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 616.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 18:39:01 | ||
图片预览





文档简介
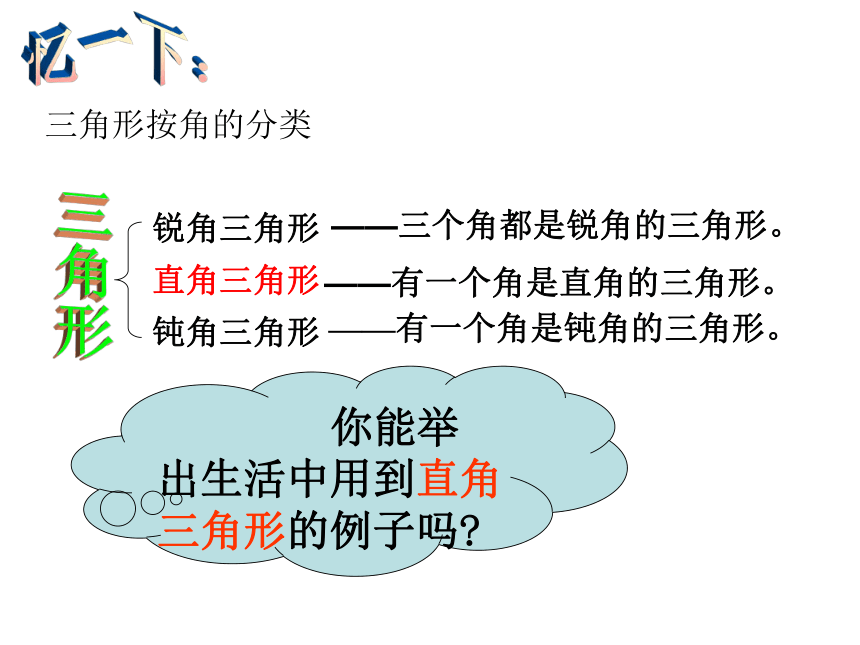
锐角三角形
直角三角形
钝角三角形
——有一个角是钝角的三角形。
三角形按角的分类
——三个角都是锐角的三角形。
——有一个角是直角的三角形。
你能举出生活中用到直角三角形的例子吗?
在Rt△ABC中,∠C=90°,
则 :
直角三角形的再认识
斜边
练习一:
(1)如图,在Rt△MNP中,∠N=90 °,
∠ P的对边是___,∠P的邻边是__,
∠ M的对边是__, ∠M的邻边是__。
MN
PN
MN
PN
练习一:
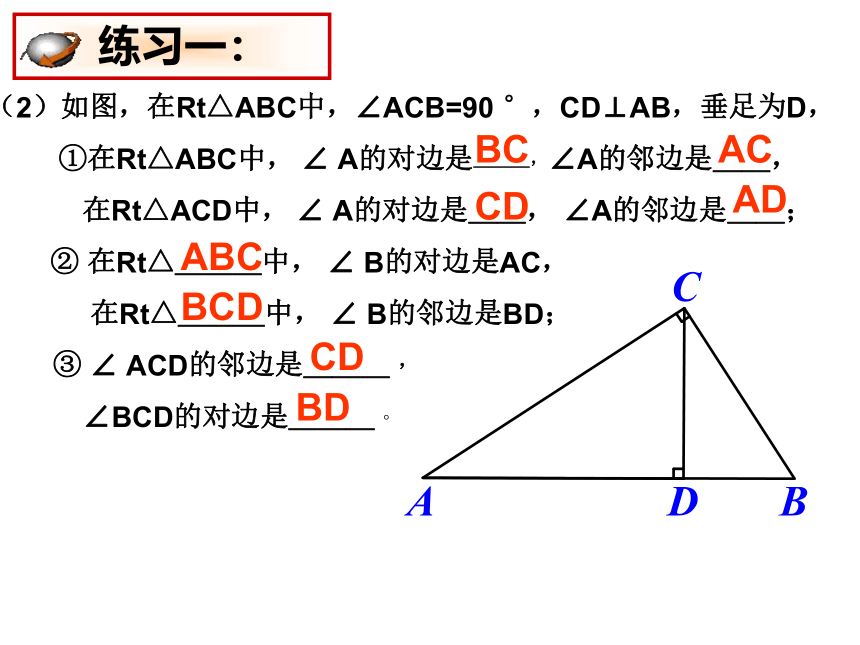
(2)如图,在Rt△ABC中,∠ACB=90 °,CD⊥AB,垂足为D,
①在Rt△ABC中, ∠ A的对边是___,∠A的邻边是__,
在Rt△ACD中, ∠ A的对边是__, ∠A的邻边是__;
② 在Rt△___中, ∠ B的对边是AC,
在Rt△___中, ∠ B的邻边是BD;
③ ∠ ACD的邻边是___ ,
∠BCD的对边是___ 。
BC
AC
AD
CD
ABC
BD
BCD
CD
每周一我校在进行升旗仪式时,当你抬头敬礼看着五星红旗冉冉升起时,你有没有想过:旗杆有多高?
Rt△ABC中,∠C=900,∠A=450,
求∠A的对边与邻边比.
C
A
B
直角三角形中,如果一个锐角等于450,那么这个角的对边与邻边的比值等于1。
450
讨论:
当∠A取其他一定度数的锐角时,
它的对边与邻边的比是否也是一个定值?
小结:
通过以上思考可以知道,在Rt△ABC中,∠C=90°,
当锐角A的大小确定后,不论Rt△ABC的边长怎样变化,
∠A的对边BC与邻边AC的比值总是确定的。
概念辨析:
则tanA=
我们把直角三角形中一个锐角的对边与邻边的比叫做这
个锐角的正切(tangent).如锐角A的正切记作tanA。
如图,在Rt△ABC中, ∠C=90°,
∠A、∠B、∠C所对的边分别记为a、b、c,
tanB=
例题分析:
例1:在Rt⊿ABC中,∠C=900,AC=3,BC=2,
求tanA和tanB的值。
3
2
解:
概念辨析:
则cotA=
我们把直角三角形中一个锐角的邻边与对边的比叫做这
个锐角的余切(cotangent).如锐角A的余切记作cotA。
cotB=
例题分析:
例1:在Rt⊿ABC中,∠C=900,AC=3,BC=2,
求tanA和tanB的值。
cotA、cotB呢?
3
2
解:
例题分析:
例2:在Rt⊿ABC中,∠C=90°,BC=4,AB=6,
求∠ A的正切与余切。
.
4
6
B
C
A
例题分析:
例3 在△ABC中,∠C=90°,BC=3,tanA= ,
求边AC的长。
3
巩固练习:
tanB,
cotA,
cot ∠ BCD
tan ∠ ACD,
(1)tanA=_________________________
(3)若AC=7,BC=3,求tan∠BCD的值
小结:
.
通过这节课的学习,你有什么新的收获?
作业:课后检测单
1.同一个锐角的正切和余切互为倒数。
3.相等的锐角的正切和余切值分别相等。
2.互余的两个角的正切和余切相等。
直角三角形
钝角三角形
——有一个角是钝角的三角形。
三角形按角的分类
——三个角都是锐角的三角形。
——有一个角是直角的三角形。
你能举出生活中用到直角三角形的例子吗?
在Rt△ABC中,∠C=90°,
则 :
直角三角形的再认识
斜边
练习一:
(1)如图,在Rt△MNP中,∠N=90 °,
∠ P的对边是___,∠P的邻边是__,
∠ M的对边是__, ∠M的邻边是__。
MN
PN
MN
PN
练习一:
(2)如图,在Rt△ABC中,∠ACB=90 °,CD⊥AB,垂足为D,
①在Rt△ABC中, ∠ A的对边是___,∠A的邻边是__,
在Rt△ACD中, ∠ A的对边是__, ∠A的邻边是__;
② 在Rt△___中, ∠ B的对边是AC,
在Rt△___中, ∠ B的邻边是BD;
③ ∠ ACD的邻边是___ ,
∠BCD的对边是___ 。
BC
AC
AD
CD
ABC
BD
BCD
CD
每周一我校在进行升旗仪式时,当你抬头敬礼看着五星红旗冉冉升起时,你有没有想过:旗杆有多高?
Rt△ABC中,∠C=900,∠A=450,
求∠A的对边与邻边比.
C
A
B
直角三角形中,如果一个锐角等于450,那么这个角的对边与邻边的比值等于1。
450
讨论:
当∠A取其他一定度数的锐角时,
它的对边与邻边的比是否也是一个定值?
小结:
通过以上思考可以知道,在Rt△ABC中,∠C=90°,
当锐角A的大小确定后,不论Rt△ABC的边长怎样变化,
∠A的对边BC与邻边AC的比值总是确定的。
概念辨析:
则tanA=
我们把直角三角形中一个锐角的对边与邻边的比叫做这
个锐角的正切(tangent).如锐角A的正切记作tanA。
如图,在Rt△ABC中, ∠C=90°,
∠A、∠B、∠C所对的边分别记为a、b、c,
tanB=
例题分析:
例1:在Rt⊿ABC中,∠C=900,AC=3,BC=2,
求tanA和tanB的值。
3
2
解:
概念辨析:
则cotA=
我们把直角三角形中一个锐角的邻边与对边的比叫做这
个锐角的余切(cotangent).如锐角A的余切记作cotA。
cotB=
例题分析:
例1:在Rt⊿ABC中,∠C=900,AC=3,BC=2,
求tanA和tanB的值。
cotA、cotB呢?
3
2
解:
例题分析:
例2:在Rt⊿ABC中,∠C=90°,BC=4,AB=6,
求∠ A的正切与余切。
.
4
6
B
C
A
例题分析:
例3 在△ABC中,∠C=90°,BC=3,tanA= ,
求边AC的长。
3
巩固练习:
tanB,
cotA,
cot ∠ BCD
tan ∠ ACD,
(1)tanA=_________________________
(3)若AC=7,BC=3,求tan∠BCD的值
小结:
.
通过这节课的学习,你有什么新的收获?
作业:课后检测单
1.同一个锐角的正切和余切互为倒数。
3.相等的锐角的正切和余切值分别相等。
2.互余的两个角的正切和余切相等。
