25.4 解直角三角形的应用(1)----仰角和俯角 课件(共17张PPT)
文档属性
| 名称 | 25.4 解直角三角形的应用(1)----仰角和俯角 课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 750.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 00:00:00 | ||
图片预览


文档简介
(1) 边: a2+b2=c2
1、解直角三角形的依据
(2) 角:∠ A+ ∠ B= 90?;
(3) 边角:sin、cos、tan、cot
A
C
B
a
b
c
复习回顾
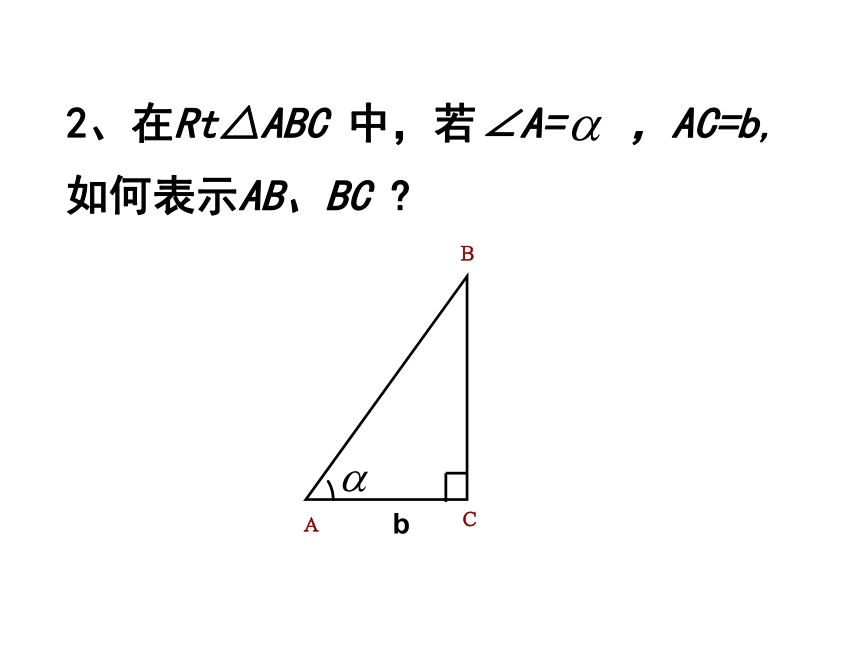
2、在Rt△ABC 中,若∠A= ,AC=b, 如何表示AB、BC ?
A
C
B
b
25.4 解直角三角形的应用(1)
----仰角和俯角
甲
铅垂线
水平线
视线
视线
仰角
俯角
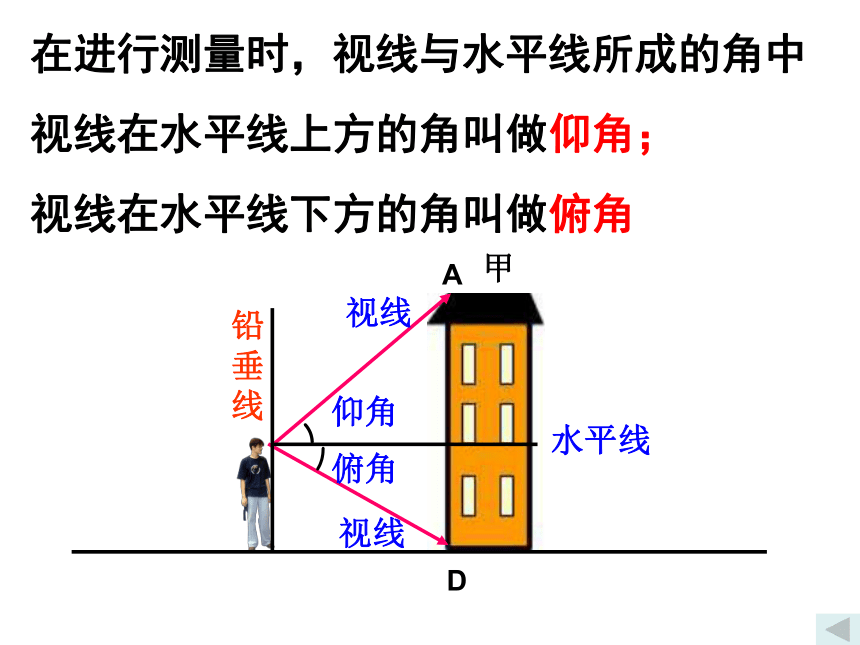
在进行测量时,视线与水平线所成的角中
视线在水平线上方的角叫做仰角;
视线在水平线下方的角叫做俯角
甲
A
D
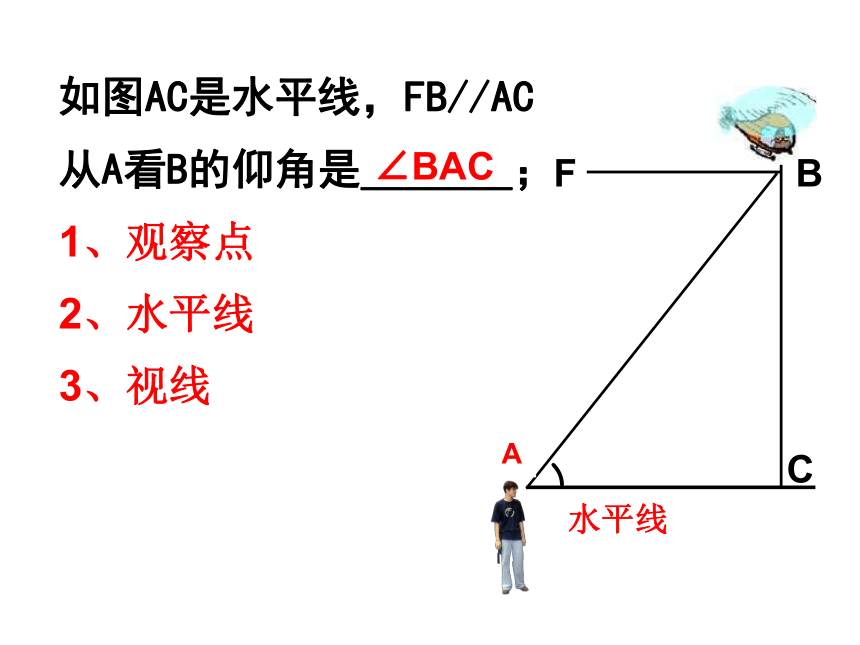
如图AC是水平线,FB//AC
从A看B的仰角是_______;
1、观察点
2、水平线
3、视线
A
C
B
F
∠BAC
水平线
A
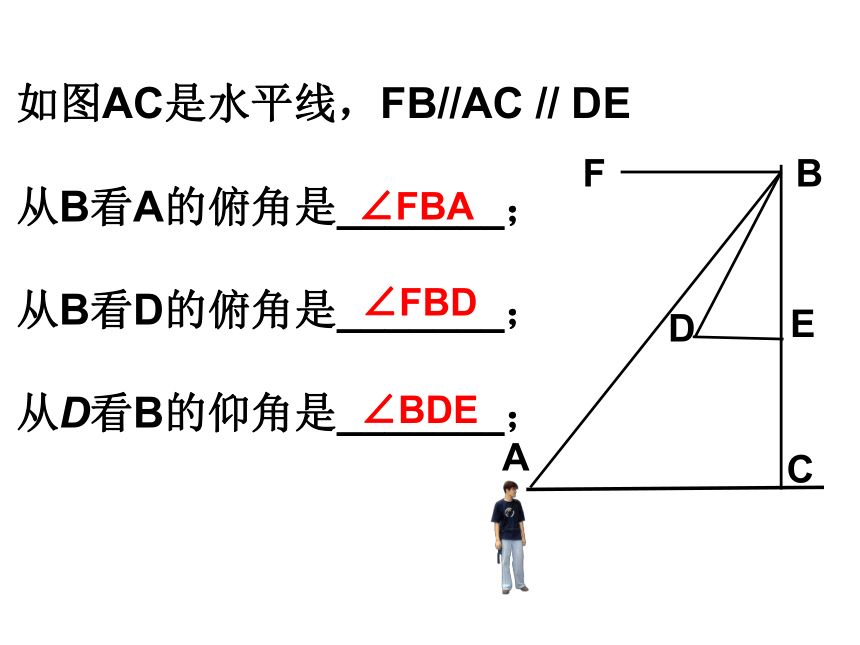
如图AC是水平线,FB//AC // DE
从B看A的俯角是_______;
从B看D的俯角是_______;
从D看B的仰角是_______;
D
A
C
E
B
F
∠FBD
∠BDE
∠FBA
1、如图,由A看向B的仰角是40°,则由B
看向A的俯角是_____.
A
B
2、在飞行高度是1000米的高空上,看到地面某标志物的俯角是30°,那么飞机与标志物之间的距离是________.
40°
2000米
测角仪
测绘员
甲
D
C
A
B
例1、测绘员在地面上离甲大楼底部C点10米的B处设立了一个观测点,利用测角仪测得顶端D处的仰角为600,已知测角仪AB的高为1.5米,求甲大楼的高度。
(精确到0.1米)
练习1、在离铁塔底部150米的C处,用测角仪测得塔顶A的仰角为30度,已知测角仪的高CD为1.5米,铁塔的高度AB为 米.
C
A
D
B
E
聚焦考点:(2015)
归纳解决实际问题的一般步骤:
(1)认真审题,构建几何模型,标记已知数据。
(2)结合所求,将实际问题中的数量关系转化为直角三角形中元素间的关系;
(3)合理选择边角关系, 求出答案。
甲
乙
A
D
C
例2、 测绘员在甲楼A处测得乙楼顶端D的仰角为450,乙楼底部C的俯角是300 ,两楼之间距离BC为60米,求出乙大楼的高度。
B
E
例3.小明所在教学楼的每层高度为3米,为了测量旗杆MN的高度,他在一楼地面的A处测得旗杆顶部M的仰角为450,他在二楼地面B处测得M的仰角为300,求旗杆MN的高度。(结果精确到0.1米, )
(第21题图)
B
A
N
M
C
例4. 小明在C处测量一座墙上的广告屏幕AB的长度,测得屏幕下端B处的仰角为300,然后他正对大楼方向前进10米到达D处,又测得该屏幕上A端处的仰角为450,已知该楼高18米,测角仪MC、ND的高度为1米.求广告屏幕AB的长.
C
N
M
D
E
B
A
F
1 、仰角,俯角的概念
2、 用解直角三角形的知识解决实际问题
1、解直角三角形的依据
(2) 角:∠ A+ ∠ B= 90?;
(3) 边角:sin、cos、tan、cot
A
C
B
a
b
c
复习回顾
2、在Rt△ABC 中,若∠A= ,AC=b, 如何表示AB、BC ?
A
C
B
b
25.4 解直角三角形的应用(1)
----仰角和俯角
甲
铅垂线
水平线
视线
视线
仰角
俯角
在进行测量时,视线与水平线所成的角中
视线在水平线上方的角叫做仰角;
视线在水平线下方的角叫做俯角
甲
A
D
如图AC是水平线,FB//AC
从A看B的仰角是_______;
1、观察点
2、水平线
3、视线
A
C
B
F
∠BAC
水平线
A
如图AC是水平线,FB//AC // DE
从B看A的俯角是_______;
从B看D的俯角是_______;
从D看B的仰角是_______;
D
A
C
E
B
F
∠FBD
∠BDE
∠FBA
1、如图,由A看向B的仰角是40°,则由B
看向A的俯角是_____.
A
B
2、在飞行高度是1000米的高空上,看到地面某标志物的俯角是30°,那么飞机与标志物之间的距离是________.
40°
2000米
测角仪
测绘员
甲
D
C
A
B
例1、测绘员在地面上离甲大楼底部C点10米的B处设立了一个观测点,利用测角仪测得顶端D处的仰角为600,已知测角仪AB的高为1.5米,求甲大楼的高度。
(精确到0.1米)
练习1、在离铁塔底部150米的C处,用测角仪测得塔顶A的仰角为30度,已知测角仪的高CD为1.5米,铁塔的高度AB为 米.
C
A
D
B
E
聚焦考点:(2015)
归纳解决实际问题的一般步骤:
(1)认真审题,构建几何模型,标记已知数据。
(2)结合所求,将实际问题中的数量关系转化为直角三角形中元素间的关系;
(3)合理选择边角关系, 求出答案。
甲
乙
A
D
C
例2、 测绘员在甲楼A处测得乙楼顶端D的仰角为450,乙楼底部C的俯角是300 ,两楼之间距离BC为60米,求出乙大楼的高度。
B
E
例3.小明所在教学楼的每层高度为3米,为了测量旗杆MN的高度,他在一楼地面的A处测得旗杆顶部M的仰角为450,他在二楼地面B处测得M的仰角为300,求旗杆MN的高度。(结果精确到0.1米, )
(第21题图)
B
A
N
M
C
例4. 小明在C处测量一座墙上的广告屏幕AB的长度,测得屏幕下端B处的仰角为300,然后他正对大楼方向前进10米到达D处,又测得该屏幕上A端处的仰角为450,已知该楼高18米,测角仪MC、ND的高度为1米.求广告屏幕AB的长.
C
N
M
D
E
B
A
F
1 、仰角,俯角的概念
2、 用解直角三角形的知识解决实际问题
