25.1 锐角三角比的意义 说课稿 课件(共30张PPT)
文档属性
| 名称 | 25.1 锐角三角比的意义 说课稿 课件(共30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 00:00:00 | ||
图片预览









文档简介
锐角三角比的意义(一)
说课稿
教学背景
教学过程
教法分析
学法分析
板书设计
一、教学背景
1.内容地位:
本节课上海教育出版社初中数学九年级第一学期25章第一课时《锐角三角比的意义》的内容。锐角三角比是在直角三角形中边边关系(勾股定理),角角关系(直角三角形两个锐角互余)的基础上,进一步研究直角三角形中边与角的关系。是后面解直角三角形的奠基石。
一、教学背景
2.教学思想:
在教学中力图让学生感受数形结合思想,体会数形结合的数学方法。
一、教学背景
3.学情分析:
九年级学生两级分化相对比较严重,面对问题探索热情不是很高涨,但是重在踏实认真,所以对于课上所授基本上可以吸收。
针对本班学情在教学设计中考虑到分层训练。
一、教学背景
4.教学目标:
掌握锐角的正切和余切的概念及相互关系、应用概念求锐角的正切、余切值;
探究锐角正切和余切的概念中,具有“实验—观察—猜想—证明”的经历,感受数学发现、创造的历程。
通过积极参与数学学习和解决问题的活动,初步养成积极探究的态度、独立思考的习惯和团队合作精神。
一、教学背景
5.教学重难点:
教学重点:锐角的正切和余切的意义。
教学难点:锐角的正切和余切表示法的理解和正确运用。
二、教法分析
实验教学法
利用“上海环球金融中心”和“金字塔”高度测量,激发学生的求知欲
启发教学法
用启发式问题教学。?
三、学法分析
自主学习法
合作交流法
实践操作法?
四、教学过程
情境创设 → 合作探究 → 概念总结→
(2分钟) (5分钟) (10分钟)
例题引导 → 课堂小结 → 作业布置
(20分钟) (2分钟) (1分钟)
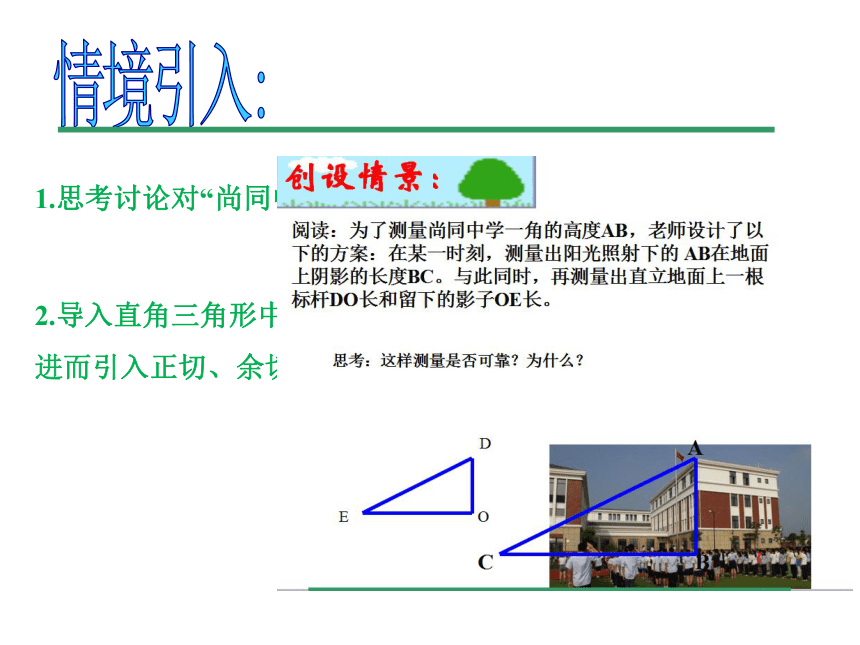
1.思考讨论对“尚同中学一角”的高度测量,
2.导入直角三角形中一个锐角确定,它的对边与邻边的比值确定,进而引入正切、余切概念。
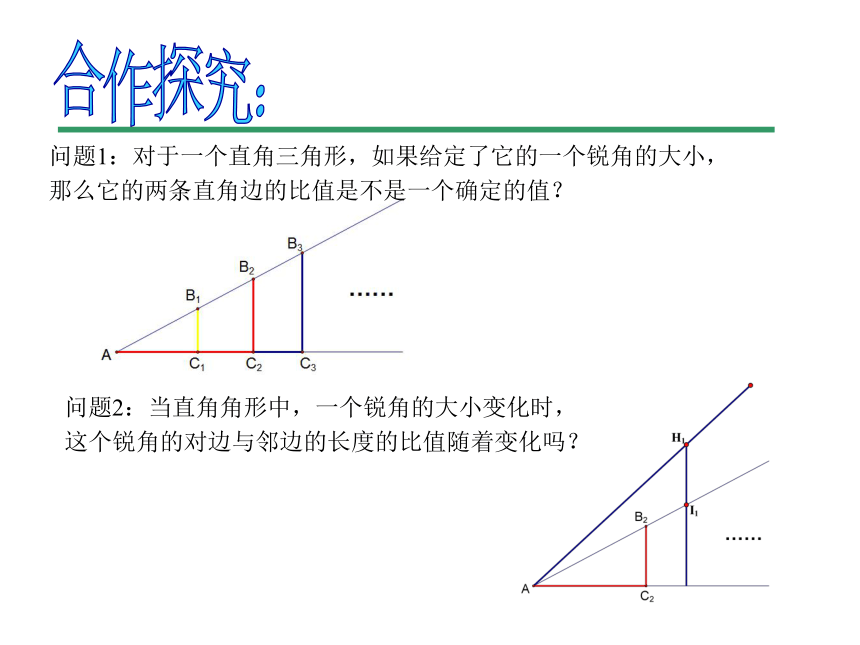
问题1:对于一个直角三角形,如果给定了它的一个锐角的大小,
那么它的两条直角边的比值是不是一个确定的值?
问题2:当直角角形中,一个锐角的大小变化时,
这个锐角的对边与邻边的长度的比值随着变化吗?
b
a
c
A
C
B
大写字母C表示Rt△ABC的直角,
小写字母a表示∠A的对边,b表示∠B的对边,c表示斜边。
(引出模型:)
b
a
c
A
C
B
试一试:在Rt△ABC中,∠C=90°,表示出锐角B的正切和余切?
锐角的正切和余切概念的得出:
把锐角A的对边(BC)与邻边(AC)的比叫做锐角A的正切。记作:tanA。
即:
把锐角A的邻边(AC)与对边(BC)的比叫做锐角A的余切。记作:cotA。
即:
1.(同桌互答)如图,在Rt△ABC和Rt△MNP中,∠C=∠N=90°
角A的对边是___________,角A的邻边是___________,tanA=____,cotA=____
角P的对边是___________,角P的邻边是___________,tanP=____,cotP=____
2.概念辨析:
①.在Rt△ABC中,tanA= 。 ( )
②.在△ABC中,tanA= 。( )
③.如果直角三角形ABC的各边的长度都扩大到原来的3倍,那么锐角A的正切、余切的值也扩大原来的3倍。( )
例1:在Rt△ABC中,∠C=90°,AC=12,BC=7,
求:(1)tanA和tanB的值 (2)cotA和cotB的值
(抽两名学生回答,老师板演)
解题过程:①根据题意,画出图形
②强调解题过程的完整性。
①同一个锐角中,tanA和cotA之间有什么关系?
②两个互余的锐角中,tanA和cotB之间有什么关系?tanB和 cotA之间有什么关系?
想一想:
例1:在Rt⊿ABC中,∠C=90°AC=2,BC=3,求tanA、cotA、tanB、cotB的值.
例题讲解:
例1:在Rt⊿ABC中,∠C=90°AC=2,BC=3,求tanA、cotA、tanB、cotB的值.
变式训练:
过点C做CD⊥AB,垂足为D,求tan∠ACD的值。
D
变式训练:
例1:在Rt⊿ABC中∠C=90°AC=2,tanA= ,求BC的值.
练习:1.如图,△ABC是直角三角形,∠C=90°,D、E在BC上,AC=4,BD=5,DE=2,EC=3,∠ABC=α,∠ADC=β,∠AEC=γ。
求:(1)tanα; (2)tanβ; (3)tanγ
A
g
b
a
D
B
E
C
5
2
3
4
2、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,找出与cotB相等的所有的线段的比。
D
C
A
B
D
C
A
D
C
B
C
A
B
1、熟悉直角三角形中锐角的对边和锐角的邻边。
2、正切和余切的概念。
3、同一个锐角的正切和余切的关系;
互余的两个锐角的正切和余切的关系
(学生自主小结)
1、必做题:练习册 习题25.1(1)
2、兴趣题:请大家运用今天所学的知识,测量学校国旗的旗杆高度。
五、板书设计
25.1(1)锐角三角比的意义
投影学生练习
…………
一、正切和余切的意义:
…………
二、同一个锐角的正切和余切的关系:
…………
互余的两个锐角的正切和余切的关系:
…………
例1的解题过程:
…………
例2的解题过程:
…………
1.情境引入:
本节课是锐角三角比的第一个课时,之前的预设里,情境引入要多花时间,但反复考虑本节课的内容比较多,重点难点想要突破一定要精简时间,所以选择在情境引入只花3分钟,可能气氛不太好,而且后面作业里,最好是可以让他们真正做这个实验。
反思:引入一定要精简,衔接恰当。
2.合作探究
是用的课本上的两个问题,发现特征,但是反复琢磨,结合课堂效果,我认为还是用第一个问题直接引入简洁明了,第二个问题可以在引入概念后进行反问。
反思:合作探究终究要为课堂重点服务,能直接引入。
3.概念总结
我认为提醒学生三角比的表示这里算是亮点吧,因为这是在我翻看练习册里面各种角度表示正切会出现错误
反思:课前一定要从教辅材料与历年试卷中研究考点与重点。
4.例题引导
在例题的设计里,我反复琢磨了课本上的例题,但是都是最简单的直接应用,学生完全可以口答的,所以我将例1反复使用,将其变式,直接考试重点,以一变三,这也是设计的亮点吧
反思:例题是提高课堂效率的最佳途径,课本中的例题内容不同,但本质是相同的,为什么不选择用一个例题引申出系列题目呢?
说课稿
教学背景
教学过程
教法分析
学法分析
板书设计
一、教学背景
1.内容地位:
本节课上海教育出版社初中数学九年级第一学期25章第一课时《锐角三角比的意义》的内容。锐角三角比是在直角三角形中边边关系(勾股定理),角角关系(直角三角形两个锐角互余)的基础上,进一步研究直角三角形中边与角的关系。是后面解直角三角形的奠基石。
一、教学背景
2.教学思想:
在教学中力图让学生感受数形结合思想,体会数形结合的数学方法。
一、教学背景
3.学情分析:
九年级学生两级分化相对比较严重,面对问题探索热情不是很高涨,但是重在踏实认真,所以对于课上所授基本上可以吸收。
针对本班学情在教学设计中考虑到分层训练。
一、教学背景
4.教学目标:
掌握锐角的正切和余切的概念及相互关系、应用概念求锐角的正切、余切值;
探究锐角正切和余切的概念中,具有“实验—观察—猜想—证明”的经历,感受数学发现、创造的历程。
通过积极参与数学学习和解决问题的活动,初步养成积极探究的态度、独立思考的习惯和团队合作精神。
一、教学背景
5.教学重难点:
教学重点:锐角的正切和余切的意义。
教学难点:锐角的正切和余切表示法的理解和正确运用。
二、教法分析
实验教学法
利用“上海环球金融中心”和“金字塔”高度测量,激发学生的求知欲
启发教学法
用启发式问题教学。?
三、学法分析
自主学习法
合作交流法
实践操作法?
四、教学过程
情境创设 → 合作探究 → 概念总结→
(2分钟) (5分钟) (10分钟)
例题引导 → 课堂小结 → 作业布置
(20分钟) (2分钟) (1分钟)
1.思考讨论对“尚同中学一角”的高度测量,
2.导入直角三角形中一个锐角确定,它的对边与邻边的比值确定,进而引入正切、余切概念。
问题1:对于一个直角三角形,如果给定了它的一个锐角的大小,
那么它的两条直角边的比值是不是一个确定的值?
问题2:当直角角形中,一个锐角的大小变化时,
这个锐角的对边与邻边的长度的比值随着变化吗?
b
a
c
A
C
B
大写字母C表示Rt△ABC的直角,
小写字母a表示∠A的对边,b表示∠B的对边,c表示斜边。
(引出模型:)
b
a
c
A
C
B
试一试:在Rt△ABC中,∠C=90°,表示出锐角B的正切和余切?
锐角的正切和余切概念的得出:
把锐角A的对边(BC)与邻边(AC)的比叫做锐角A的正切。记作:tanA。
即:
把锐角A的邻边(AC)与对边(BC)的比叫做锐角A的余切。记作:cotA。
即:
1.(同桌互答)如图,在Rt△ABC和Rt△MNP中,∠C=∠N=90°
角A的对边是___________,角A的邻边是___________,tanA=____,cotA=____
角P的对边是___________,角P的邻边是___________,tanP=____,cotP=____
2.概念辨析:
①.在Rt△ABC中,tanA= 。 ( )
②.在△ABC中,tanA= 。( )
③.如果直角三角形ABC的各边的长度都扩大到原来的3倍,那么锐角A的正切、余切的值也扩大原来的3倍。( )
例1:在Rt△ABC中,∠C=90°,AC=12,BC=7,
求:(1)tanA和tanB的值 (2)cotA和cotB的值
(抽两名学生回答,老师板演)
解题过程:①根据题意,画出图形
②强调解题过程的完整性。
①同一个锐角中,tanA和cotA之间有什么关系?
②两个互余的锐角中,tanA和cotB之间有什么关系?tanB和 cotA之间有什么关系?
想一想:
例1:在Rt⊿ABC中,∠C=90°AC=2,BC=3,求tanA、cotA、tanB、cotB的值.
例题讲解:
例1:在Rt⊿ABC中,∠C=90°AC=2,BC=3,求tanA、cotA、tanB、cotB的值.
变式训练:
过点C做CD⊥AB,垂足为D,求tan∠ACD的值。
D
变式训练:
例1:在Rt⊿ABC中∠C=90°AC=2,tanA= ,求BC的值.
练习:1.如图,△ABC是直角三角形,∠C=90°,D、E在BC上,AC=4,BD=5,DE=2,EC=3,∠ABC=α,∠ADC=β,∠AEC=γ。
求:(1)tanα; (2)tanβ; (3)tanγ
A
g
b
a
D
B
E
C
5
2
3
4
2、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,找出与cotB相等的所有的线段的比。
D
C
A
B
D
C
A
D
C
B
C
A
B
1、熟悉直角三角形中锐角的对边和锐角的邻边。
2、正切和余切的概念。
3、同一个锐角的正切和余切的关系;
互余的两个锐角的正切和余切的关系
(学生自主小结)
1、必做题:练习册 习题25.1(1)
2、兴趣题:请大家运用今天所学的知识,测量学校国旗的旗杆高度。
五、板书设计
25.1(1)锐角三角比的意义
投影学生练习
…………
一、正切和余切的意义:
…………
二、同一个锐角的正切和余切的关系:
…………
互余的两个锐角的正切和余切的关系:
…………
例1的解题过程:
…………
例2的解题过程:
…………
1.情境引入:
本节课是锐角三角比的第一个课时,之前的预设里,情境引入要多花时间,但反复考虑本节课的内容比较多,重点难点想要突破一定要精简时间,所以选择在情境引入只花3分钟,可能气氛不太好,而且后面作业里,最好是可以让他们真正做这个实验。
反思:引入一定要精简,衔接恰当。
2.合作探究
是用的课本上的两个问题,发现特征,但是反复琢磨,结合课堂效果,我认为还是用第一个问题直接引入简洁明了,第二个问题可以在引入概念后进行反问。
反思:合作探究终究要为课堂重点服务,能直接引入。
3.概念总结
我认为提醒学生三角比的表示这里算是亮点吧,因为这是在我翻看练习册里面各种角度表示正切会出现错误
反思:课前一定要从教辅材料与历年试卷中研究考点与重点。
4.例题引导
在例题的设计里,我反复琢磨了课本上的例题,但是都是最简单的直接应用,学生完全可以口答的,所以我将例1反复使用,将其变式,直接考试重点,以一变三,这也是设计的亮点吧
反思:例题是提高课堂效率的最佳途径,课本中的例题内容不同,但本质是相同的,为什么不选择用一个例题引申出系列题目呢?
