人教版八年级数学上册13.3.2等边三角形 课件(共28张PPT)
文档属性
| 名称 | 人教版八年级数学上册13.3.2等边三角形 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 24.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 19:05:58 | ||
图片预览



文档简介
第十三章 轴对称
13.3.2 等边三角形
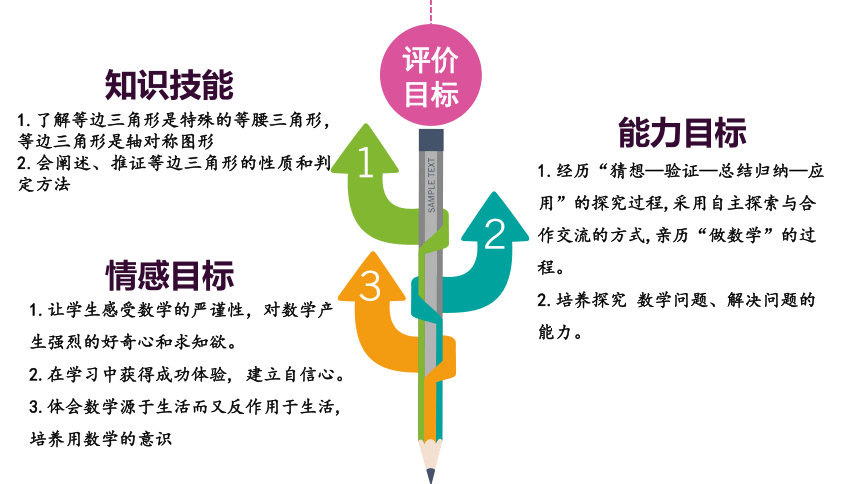
能力目标
1.经历“猜想—验证—总结归纳—应用”的探究过程,采用自主探索与合作交流的方式,亲历“做数学”的过程。
2.培养探究 数学问题、解决问题的能力。
知识技能
1.了解等边三角形是特殊的等腰三角形,等边三角形是轴对称图形
2.会阐述、推证等边三角形的性质和判定方法
情感目标
1.让学生感受数学的严谨性,对数学产生强烈的好奇心和求知欲。
2.在学习中获得成功体验, 建立自信心。
3.体会数学源于生活而又反作用于生活,培养用数学的意识
评价
目标
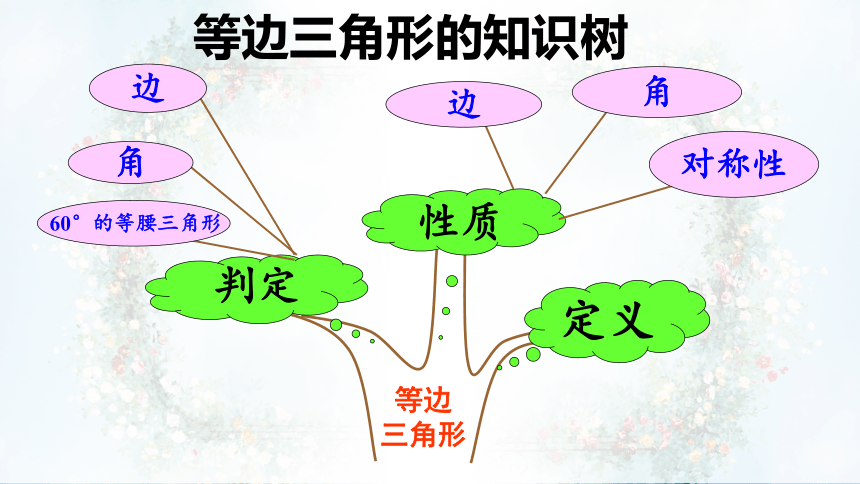
等边
三角形
判定
性质
定义
边
角
对称性
边
角
60°的等腰三角形
等边三角形的知识树
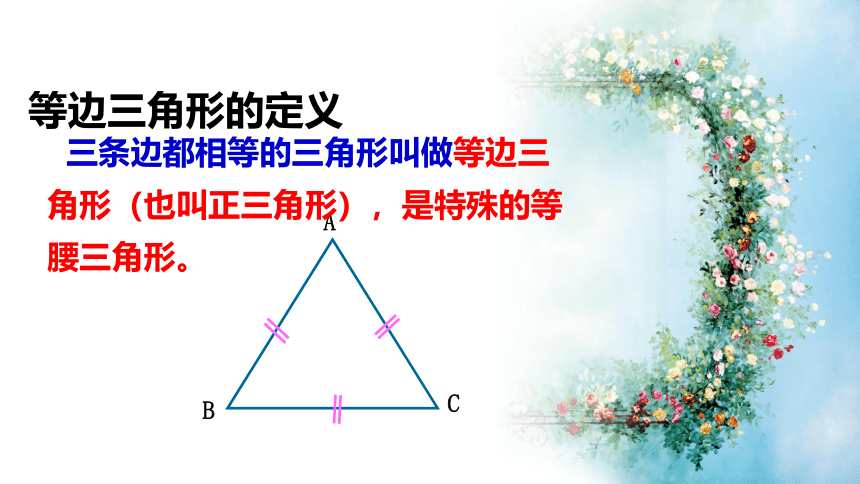
A
B
C
三条边都相等的三角形叫做等边三角形(也叫正三角形),是特殊的等腰三角形。
等边三角形的定义
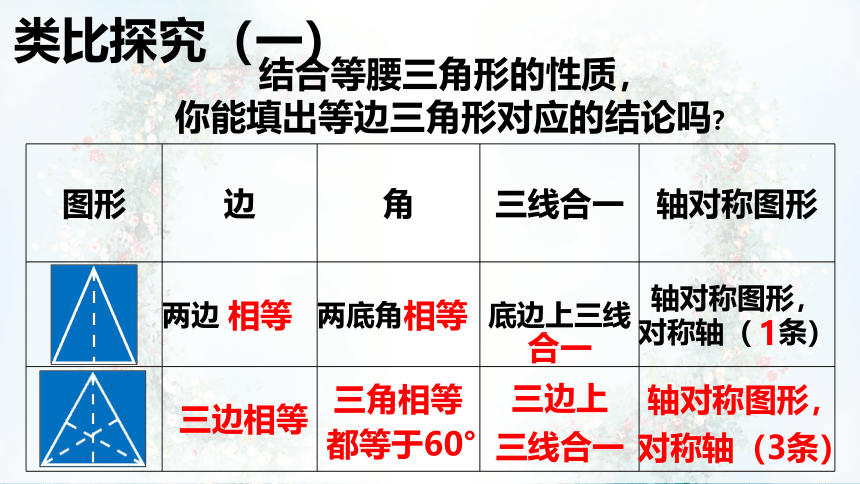
类比探究(一)
结合等腰三角形的性质,
你能填出等边三角形对应的结论吗?
图形
边
角
三线合一
轴对称图形
两边
两底角
底边上三线
轴对称图形,对称轴( 条)
三边相等
三角相等
都等于60°
三边上
三线合一
轴对称图形,对称轴(3条)
相等
相等
合一
1
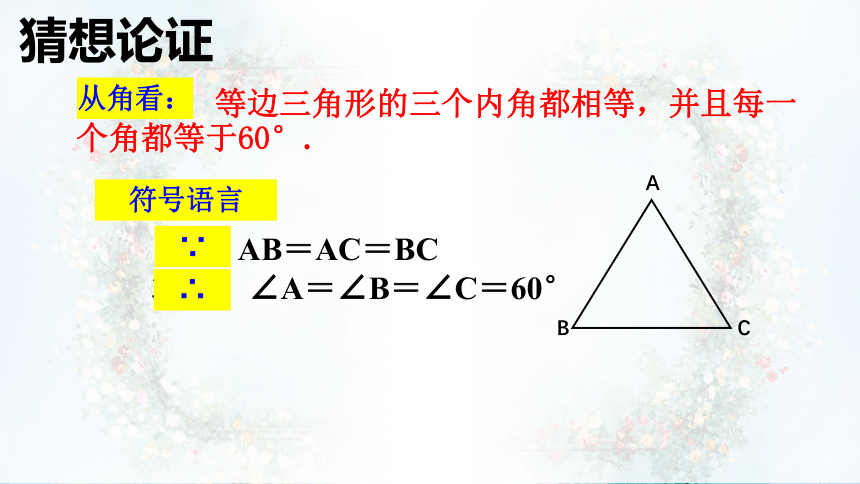
猜想一:等边三角形的三个内角都相等,并且每一个角都等于60°.
已知:AB=AC=BC
求证:∠A=∠B=∠C=60°
A
B
C
从角看:
∵
∴
符号语言
猜想论证
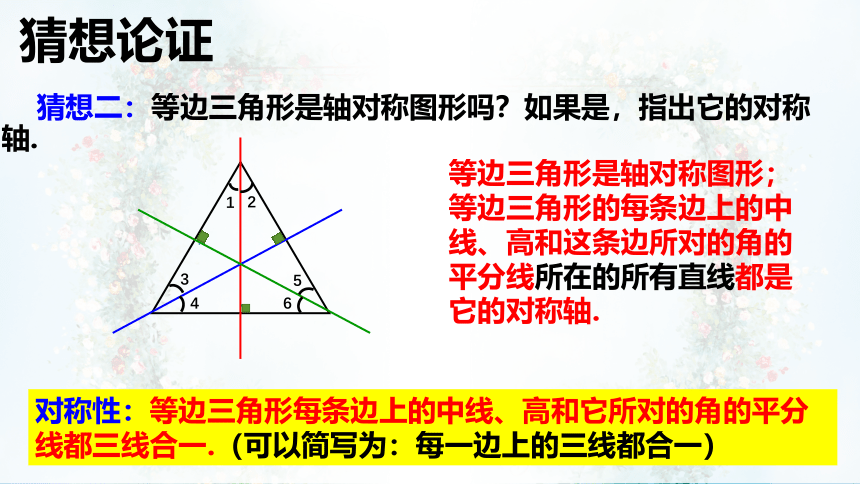
猜想二:等边三角形是轴对称图形吗?如果是,指出它的对称轴.
等边三角形是轴对称图形;
等边三角形的每条边上的中线、高和这条边所对的角的平分线所在的所有直线都是它的对称轴.
对称性:等边三角形每条边上的中线、高和它所对的角的平分线都三线合一.(可以简写为:每一边上的三线都合一)
猜想论证
1
2
6
5
4
3
图形
等腰三角形
等边三角形
性 质
边
两条边相等
角
两个底角相等
三线合一
底边上的中线、高和顶角的平分线互相重合
对称性
轴对称图形,对称轴(1条)
每一边上的中线、高和它所对的角的平分线互相重合
三个角都相等
轴对称图形,对称轴(3条)
三条边都相等
性质对比
思维小结
1.三边都相等的三角形叫做____三角形.
2.等边三角形的每个内角都等于____度.
3.等边三角形有____条对称轴.
等边
60
3
新知运用
思维训练
1、△ABC是等边三角形,周长为15cm,则BC=_______
A
B
C
2.如图,等边三角形ABC中,AD 是 BC 边上的中线,AD=AE,则∠EDC的度数是( ).
A.13 ° B.14 ° C.15 ° D.30°
有两边相等的三角形
是等腰三角形(定义)
有两个角相等的三角形是等腰三角形。
满足什么条件的三角形是等边三角形?
满足什么条件的三角形是等腰三角形?
三边都相等的三角形
是等边三角形(定义)
三个角都相等的三角形
是等边三角形。
方法一:从边看
方法二:从角看
方法一:从边看
猜想二:从角看
类比探究(二)
猜想:三个角都相等的三角形是等边三角形
已知:∠A=∠B=∠C
求证:AB=BC=AC
A
B
C
从角看
符号语言
∵
∴
猜想论证
这个60°角的位置有哪几种情况呢?
60°角是等腰三角形的顶角
60°角是等腰三角形的底角
有一个角是60°的等腰三角形一定是等边三角形吗?
思维延伸
分类讨论思想
详细内容……点击输入本栏的具体文字,简明扼要的说明分项内容,此为概念图解。
详细内容……点击输入本栏的具体文字,简明扼要的说明分项内容,此为概念图解。
详细内容……点击输入本栏的具体文字,简明扼要的说明分项内容,此为概念图解。
详细内容……点击输入本的具体文字,简明扼要的说明分项内容,此为概念图解。
猜想三: 有一个角是60°的等腰三角
形是等边三角形
A
B
C
特殊等腰三角形
∵AB=AC,
∠A=60°(或∠B=60°)
∴AB=BC=AC
符号语言
猜想论证
详细内容……点击输入本栏的具体文字,简明扼要的说明分项内容,此为概念图解。
详细内容……点击输入本栏的具体文字,简明扼要的说明分项内容,此为概念图解。
详细内容……点击输入本栏的具体文字,简明扼要的说明分项内容,此为概念图解。
详细内容……点击输入本的具体文字,简明扼要的说明分项内容,此为概念图解。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}方法1(从边看)
方法2(从角看)
方法3(特殊等腰三角形)
三边相等的三角形是等边三角形
三角相等的三角形是等边三角形
有一个角是60°的等腰三角形是等边三角形
思维小结
判定等边三角形的三种方法
详细内容……点击输入本栏的具体文字,简明扼要的说明分项内容,此为概念图解。
详细内容……点击输入本栏的具体文字,简明扼要的说明分项内容,此为概念图解。
详细内容……点击输入本栏的具体文字,简明扼要的说明分项内容,此为概念图解。
详细内容……点击输入本的具体文字,简明扼要的说明分项内容,此为概念图解。
1.根据条件判断下列三角形是否为等边三角形.
(1)
(2)
(6)
(5)
不
是
是
是
是
是
(4)
(3)
不一定
是
思维展现
2.已知:如图,P、Q是△ABC的边BC上的两点,
并且PB=PQ=QC=AP=AQ, 求∠BAC的大小.
△ABC是等边三角形,以下三种分法分别得到的△ADE是等边三角形吗,为什么?
①在边AB、AC上分别截取AD=AE.
A
C
B
①
A
C
B
②
A
C
B
③
D
E
D
E
D
E
600
②作∠ADE=600,D、E分别在边AB、AC上.
③过边AB上一点D作DE∥BC,交边AC于E点.
证明:∵△ABC是等边三角形
∴∠A=∠B=∠C=600
又∵DE∥BC
∴∠ADE=∠B,∠AED=∠C
∴∠ADE=∠A=∠AED
∴△ADE是等边三角形。
思维放飞
1.如图,等边三角形ABC中,AD是BC上的高,
∠ BDE=∠CDF=60 °,图中有哪些与BD相等的线段?
D
E
F
与BD相等的线段有:
DC、FC、FD、BE、DE、AE、AF
思维提升
2.△ABC是等边三角形,D为AC的中点,延长BC到E,使CE=CD,
求证:BD=DE
A
B
C
E
D
体会.分享
说一说这节课的收获和体验,让大家与你一起分享。
等边
三角形
定义
底=腰
特殊性
性质
特殊性
边
三边相等
角
三个角都等于60 °
轴对称性
轴对称图形,每条边上都具有“三线合一”性质
判定
特殊性
边
角
特殊等腰
三角形
思维梳理
1.已知△ABC中,∠A=∠B=60°,AB=3cm,则△ABC的周长为______cm
A
B
C
当堂达标
2.下列关于等边三角形的说法正确的有( )
①等边三角形的三个角相等,并且每一个角都是60°;
②三边相等的三角形是等边三角形;
③三角相等的三角形是等边三角形;
④有一个角是60°的等腰三角形是等边三角形.
A.①②③ B.①②④
C.②③④ D.①②③④
如图所示, △ ABC为等边三角形,且∠1=∠2=∠3
(1)求∠BEC的度数
(2) △ DEF是等边三角形吗?请说明理由
思维拓展
变式练习
如图,等边△ABC中,D. E.?F分别是各边上的一点,
且AD=BE=CF.
求证:△DEF是等边三角形。
教师寄语
给我最大快乐的,不是已懂得知识,而是不断的学习;不是已有的东西,而是不断的获取;不是已达到的高度,而是继续不断的攀登。——高斯
13.3.2 等边三角形
能力目标
1.经历“猜想—验证—总结归纳—应用”的探究过程,采用自主探索与合作交流的方式,亲历“做数学”的过程。
2.培养探究 数学问题、解决问题的能力。
知识技能
1.了解等边三角形是特殊的等腰三角形,等边三角形是轴对称图形
2.会阐述、推证等边三角形的性质和判定方法
情感目标
1.让学生感受数学的严谨性,对数学产生强烈的好奇心和求知欲。
2.在学习中获得成功体验, 建立自信心。
3.体会数学源于生活而又反作用于生活,培养用数学的意识
评价
目标
等边
三角形
判定
性质
定义
边
角
对称性
边
角
60°的等腰三角形
等边三角形的知识树
A
B
C
三条边都相等的三角形叫做等边三角形(也叫正三角形),是特殊的等腰三角形。
等边三角形的定义
类比探究(一)
结合等腰三角形的性质,
你能填出等边三角形对应的结论吗?
图形
边
角
三线合一
轴对称图形
两边
两底角
底边上三线
轴对称图形,对称轴( 条)
三边相等
三角相等
都等于60°
三边上
三线合一
轴对称图形,对称轴(3条)
相等
相等
合一
1
猜想一:等边三角形的三个内角都相等,并且每一个角都等于60°.
已知:AB=AC=BC
求证:∠A=∠B=∠C=60°
A
B
C
从角看:
∵
∴
符号语言
猜想论证
猜想二:等边三角形是轴对称图形吗?如果是,指出它的对称轴.
等边三角形是轴对称图形;
等边三角形的每条边上的中线、高和这条边所对的角的平分线所在的所有直线都是它的对称轴.
对称性:等边三角形每条边上的中线、高和它所对的角的平分线都三线合一.(可以简写为:每一边上的三线都合一)
猜想论证
1
2
6
5
4
3
图形
等腰三角形
等边三角形
性 质
边
两条边相等
角
两个底角相等
三线合一
底边上的中线、高和顶角的平分线互相重合
对称性
轴对称图形,对称轴(1条)
每一边上的中线、高和它所对的角的平分线互相重合
三个角都相等
轴对称图形,对称轴(3条)
三条边都相等
性质对比
思维小结
1.三边都相等的三角形叫做____三角形.
2.等边三角形的每个内角都等于____度.
3.等边三角形有____条对称轴.
等边
60
3
新知运用
思维训练
1、△ABC是等边三角形,周长为15cm,则BC=_______
A
B
C
2.如图,等边三角形ABC中,AD 是 BC 边上的中线,AD=AE,则∠EDC的度数是( ).
A.13 ° B.14 ° C.15 ° D.30°
有两边相等的三角形
是等腰三角形(定义)
有两个角相等的三角形是等腰三角形。
满足什么条件的三角形是等边三角形?
满足什么条件的三角形是等腰三角形?
三边都相等的三角形
是等边三角形(定义)
三个角都相等的三角形
是等边三角形。
方法一:从边看
方法二:从角看
方法一:从边看
猜想二:从角看
类比探究(二)
猜想:三个角都相等的三角形是等边三角形
已知:∠A=∠B=∠C
求证:AB=BC=AC
A
B
C
从角看
符号语言
∵
∴
猜想论证
这个60°角的位置有哪几种情况呢?
60°角是等腰三角形的顶角
60°角是等腰三角形的底角
有一个角是60°的等腰三角形一定是等边三角形吗?
思维延伸
分类讨论思想
详细内容……点击输入本栏的具体文字,简明扼要的说明分项内容,此为概念图解。
详细内容……点击输入本栏的具体文字,简明扼要的说明分项内容,此为概念图解。
详细内容……点击输入本栏的具体文字,简明扼要的说明分项内容,此为概念图解。
详细内容……点击输入本的具体文字,简明扼要的说明分项内容,此为概念图解。
猜想三: 有一个角是60°的等腰三角
形是等边三角形
A
B
C
特殊等腰三角形
∵AB=AC,
∠A=60°(或∠B=60°)
∴AB=BC=AC
符号语言
猜想论证
详细内容……点击输入本栏的具体文字,简明扼要的说明分项内容,此为概念图解。
详细内容……点击输入本栏的具体文字,简明扼要的说明分项内容,此为概念图解。
详细内容……点击输入本栏的具体文字,简明扼要的说明分项内容,此为概念图解。
详细内容……点击输入本的具体文字,简明扼要的说明分项内容,此为概念图解。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}方法1(从边看)
方法2(从角看)
方法3(特殊等腰三角形)
三边相等的三角形是等边三角形
三角相等的三角形是等边三角形
有一个角是60°的等腰三角形是等边三角形
思维小结
判定等边三角形的三种方法
详细内容……点击输入本栏的具体文字,简明扼要的说明分项内容,此为概念图解。
详细内容……点击输入本栏的具体文字,简明扼要的说明分项内容,此为概念图解。
详细内容……点击输入本栏的具体文字,简明扼要的说明分项内容,此为概念图解。
详细内容……点击输入本的具体文字,简明扼要的说明分项内容,此为概念图解。
1.根据条件判断下列三角形是否为等边三角形.
(1)
(2)
(6)
(5)
不
是
是
是
是
是
(4)
(3)
不一定
是
思维展现
2.已知:如图,P、Q是△ABC的边BC上的两点,
并且PB=PQ=QC=AP=AQ, 求∠BAC的大小.
△ABC是等边三角形,以下三种分法分别得到的△ADE是等边三角形吗,为什么?
①在边AB、AC上分别截取AD=AE.
A
C
B
①
A
C
B
②
A
C
B
③
D
E
D
E
D
E
600
②作∠ADE=600,D、E分别在边AB、AC上.
③过边AB上一点D作DE∥BC,交边AC于E点.
证明:∵△ABC是等边三角形
∴∠A=∠B=∠C=600
又∵DE∥BC
∴∠ADE=∠B,∠AED=∠C
∴∠ADE=∠A=∠AED
∴△ADE是等边三角形。
思维放飞
1.如图,等边三角形ABC中,AD是BC上的高,
∠ BDE=∠CDF=60 °,图中有哪些与BD相等的线段?
D
E
F
与BD相等的线段有:
DC、FC、FD、BE、DE、AE、AF
思维提升
2.△ABC是等边三角形,D为AC的中点,延长BC到E,使CE=CD,
求证:BD=DE
A
B
C
E
D
体会.分享
说一说这节课的收获和体验,让大家与你一起分享。
等边
三角形
定义
底=腰
特殊性
性质
特殊性
边
三边相等
角
三个角都等于60 °
轴对称性
轴对称图形,每条边上都具有“三线合一”性质
判定
特殊性
边
角
特殊等腰
三角形
思维梳理
1.已知△ABC中,∠A=∠B=60°,AB=3cm,则△ABC的周长为______cm
A
B
C
当堂达标
2.下列关于等边三角形的说法正确的有( )
①等边三角形的三个角相等,并且每一个角都是60°;
②三边相等的三角形是等边三角形;
③三角相等的三角形是等边三角形;
④有一个角是60°的等腰三角形是等边三角形.
A.①②③ B.①②④
C.②③④ D.①②③④
如图所示, △ ABC为等边三角形,且∠1=∠2=∠3
(1)求∠BEC的度数
(2) △ DEF是等边三角形吗?请说明理由
思维拓展
变式练习
如图,等边△ABC中,D. E.?F分别是各边上的一点,
且AD=BE=CF.
求证:△DEF是等边三角形。
教师寄语
给我最大快乐的,不是已懂得知识,而是不断的学习;不是已有的东西,而是不断的获取;不是已达到的高度,而是继续不断的攀登。——高斯
