1.5.1有理数的乘方教学 课件(共17张PPT)
文档属性
| 名称 | 1.5.1有理数的乘方教学 课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 00:00:00 | ||
图片预览




文档简介
珠穆朗玛峰
把一张足够大且厚度为0.1毫米的纸,对折30次,它的厚度能超过珠穆朗玛峰吗?
的高度为8848米,
是世界最高峰,
有地球“第三极”之誉。
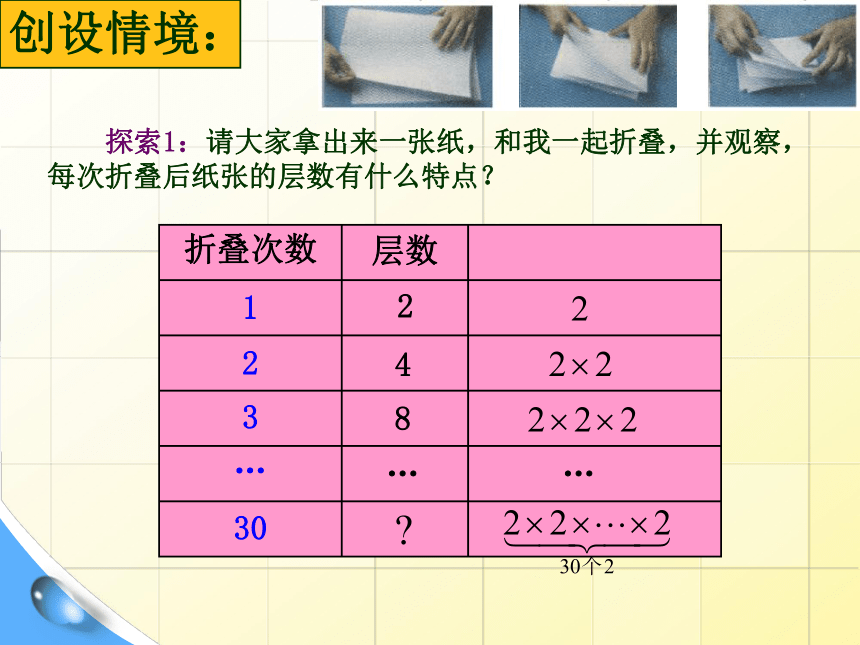
创设情境:
探索1:请大家拿出来一张纸,和我一起折叠,并观察,每次折叠后纸张的层数有什么特点?
折叠次数
层数
1
2
3
…
2
4
8
…
30
…
创设情境:
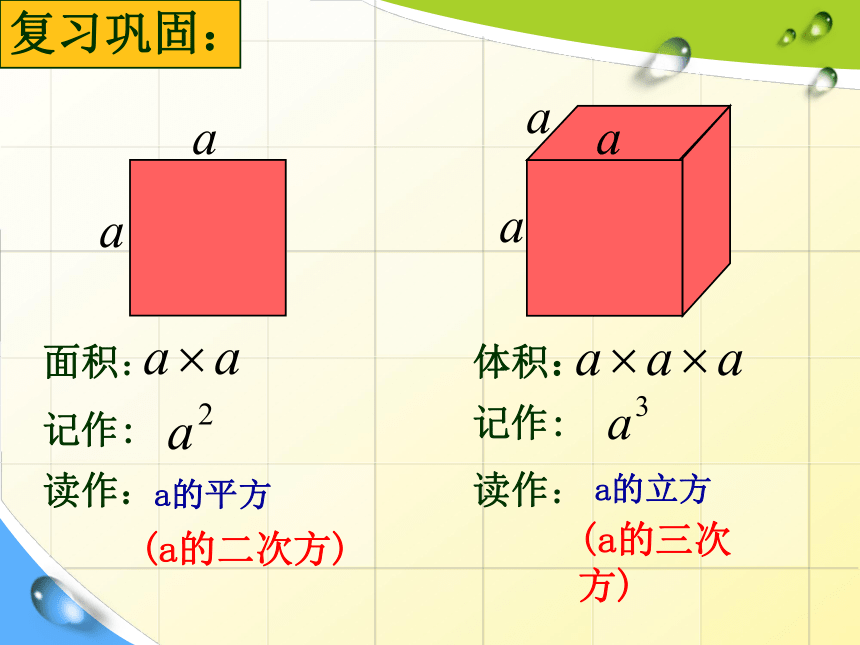
a的平方
a的立方
记作:
记作:
读作:
读作:
面积:
体积:
(a的二次方)
(a的三次方)
复习巩固:
(a的平方,或a的二次方)
怎么读呢?
(a的立方,或a的三次方)
(2的三十次方)
(2的n次方)
(a的n次方)
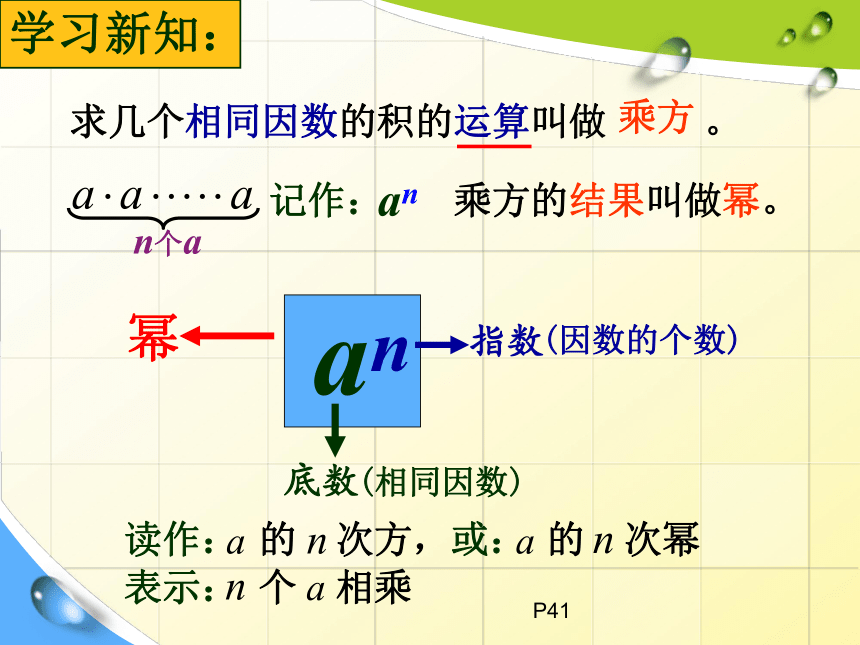
发现新知:
an
乘方的结果叫做幂。
幂
指数
(因数的个数)
底数
(相同因数)
求几个相同因数的积的运算叫做 。
记作:
an
n个a
读作: 的 次方,或: 的 次幂
表示: 个 相乘
乘方
学习新知:
P41
1、 的底数 ,
指数 ,
表示 ,
读作 ,
或者 ;
2
4
4个2相乘
2的4次方
2的4次幂
2、 的底数 ,指数 ,表示 ,
读作 ,或者 ;
-4
5
5个-4相乘
-4的5次方
-4的5次幂
3、 读作 ,或者 ,
6的2次方
6的2次幂
6的平方
4、 的底数 ,
7
注:一个数可以看作这个数本身的一次方。
指数1通常省略不写。
指数 ,
1
7可以看成 的一次方。
7
分析概念:
P41
还可读作 ;
1、 的底数为 ,
2
的底数为 ,
-2
的底数为 ,
-2
辨析概念:
2、 的底数为 ,
2
3
的底数为 ,
2
3
2
2
注意:当底数是负数或分数,
写底数时要添加括号。
辨析概念:
1、把乘法形式写成幂的形式:
(-3)×(-3)×(-3)×(-3)= ____________
4
3
( )
5
2、把幂的形式写成乘法形式:
=
(-3)
4
_________________
-5
3
- 5×5×5 = ___________
4
3
5
=
_________________
计算:
(1)
(2)
(3)
(1)
(2)
(3)
解:
注:先确定幂的符号后计算
应用概念:
计算并观察下列幂的符号与底数、指数有什么关系,你能发现什么?
(1)
(2)
(3)
(4)
正数的任何次幂都是正数;
负数的
偶次幂是正数
奇次幂是负数
0的任何正整数次幂都是0
再探概念:
1、下列式子错误的是( )
D
2、判断下列式子是否正确
-1的奇次幂是-1;
-1的偶次幂是1。
巩固概念:
(1)
(2)
(3)
( )
( )
( )
-1
3、计算:
(1)
(2)
(3)
(4)
4、计算:
(1)
(2)
巩固概念:
珠穆朗玛峰
把一张足够大且厚度为0.1毫米的纸,对折30次,它的厚度能超过珠穆朗玛峰吗?
的高度为8848米,
是世界最高峰,
有地球“第三极”之誉。
解决问题:
折纸次数 纸的厚度(毫米)
1 0.1×2
2 0.1×2×2
3 0.1×2×2×2
…
30 0.1×2×2×···×2
=0.1×22
=0.1×23
30个2
=0.1×230
0.1×230=0.1×1073741824毫米
=107374.1824米
>8848米
解决问题:
这节课你学到了什么?
这节课你有什么收获?
必做:课本P47 习题1.5 第1,7题
选做:已知: ,求:
课堂小结:
作业:
请您批评指正!
把一张足够大且厚度为0.1毫米的纸,对折30次,它的厚度能超过珠穆朗玛峰吗?
的高度为8848米,
是世界最高峰,
有地球“第三极”之誉。
创设情境:
探索1:请大家拿出来一张纸,和我一起折叠,并观察,每次折叠后纸张的层数有什么特点?
折叠次数
层数
1
2
3
…
2
4
8
…
30
…
创设情境:
a的平方
a的立方
记作:
记作:
读作:
读作:
面积:
体积:
(a的二次方)
(a的三次方)
复习巩固:
(a的平方,或a的二次方)
怎么读呢?
(a的立方,或a的三次方)
(2的三十次方)
(2的n次方)
(a的n次方)
发现新知:
an
乘方的结果叫做幂。
幂
指数
(因数的个数)
底数
(相同因数)
求几个相同因数的积的运算叫做 。
记作:
an
n个a
读作: 的 次方,或: 的 次幂
表示: 个 相乘
乘方
学习新知:
P41
1、 的底数 ,
指数 ,
表示 ,
读作 ,
或者 ;
2
4
4个2相乘
2的4次方
2的4次幂
2、 的底数 ,指数 ,表示 ,
读作 ,或者 ;
-4
5
5个-4相乘
-4的5次方
-4的5次幂
3、 读作 ,或者 ,
6的2次方
6的2次幂
6的平方
4、 的底数 ,
7
注:一个数可以看作这个数本身的一次方。
指数1通常省略不写。
指数 ,
1
7可以看成 的一次方。
7
分析概念:
P41
还可读作 ;
1、 的底数为 ,
2
的底数为 ,
-2
的底数为 ,
-2
辨析概念:
2、 的底数为 ,
2
3
的底数为 ,
2
3
2
2
注意:当底数是负数或分数,
写底数时要添加括号。
辨析概念:
1、把乘法形式写成幂的形式:
(-3)×(-3)×(-3)×(-3)= ____________
4
3
( )
5
2、把幂的形式写成乘法形式:
=
(-3)
4
_________________
-5
3
- 5×5×5 = ___________
4
3
5
=
_________________
计算:
(1)
(2)
(3)
(1)
(2)
(3)
解:
注:先确定幂的符号后计算
应用概念:
计算并观察下列幂的符号与底数、指数有什么关系,你能发现什么?
(1)
(2)
(3)
(4)
正数的任何次幂都是正数;
负数的
偶次幂是正数
奇次幂是负数
0的任何正整数次幂都是0
再探概念:
1、下列式子错误的是( )
D
2、判断下列式子是否正确
-1的奇次幂是-1;
-1的偶次幂是1。
巩固概念:
(1)
(2)
(3)
( )
( )
( )
-1
3、计算:
(1)
(2)
(3)
(4)
4、计算:
(1)
(2)
巩固概念:
珠穆朗玛峰
把一张足够大且厚度为0.1毫米的纸,对折30次,它的厚度能超过珠穆朗玛峰吗?
的高度为8848米,
是世界最高峰,
有地球“第三极”之誉。
解决问题:
折纸次数 纸的厚度(毫米)
1 0.1×2
2 0.1×2×2
3 0.1×2×2×2
…
30 0.1×2×2×···×2
=0.1×22
=0.1×23
30个2
=0.1×230
0.1×230=0.1×1073741824毫米
=107374.1824米
>8848米
解决问题:
这节课你学到了什么?
这节课你有什么收获?
必做:课本P47 习题1.5 第1,7题
选做:已知: ,求:
课堂小结:
作业:
请您批评指正!
