人教版数学八年下册16.2 二次根式的乘除 二次根式的除法 课件(共20张ppt)
文档属性
| 名称 | 人教版数学八年下册16.2 二次根式的乘除 二次根式的除法 课件(共20张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 17:49:56 | ||
图片预览





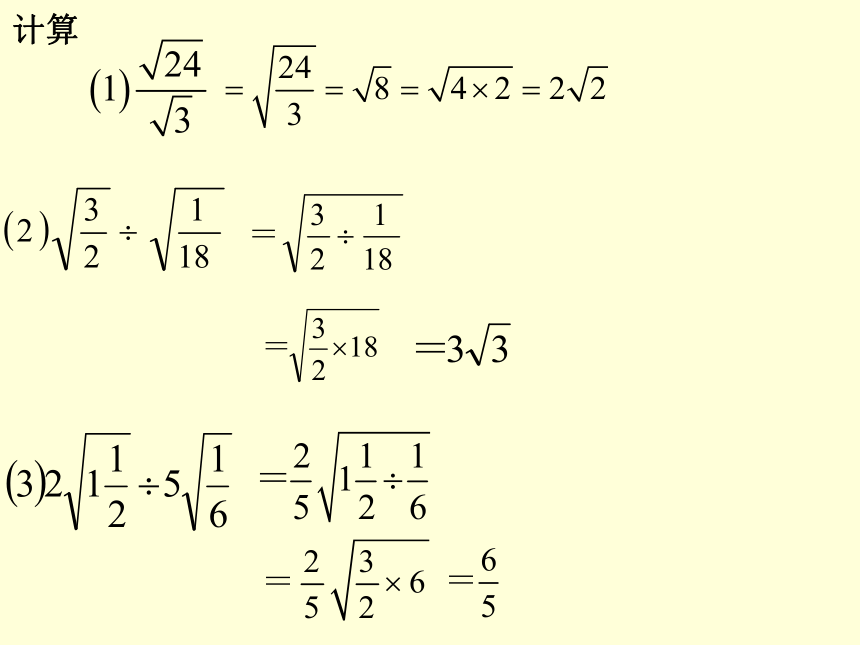
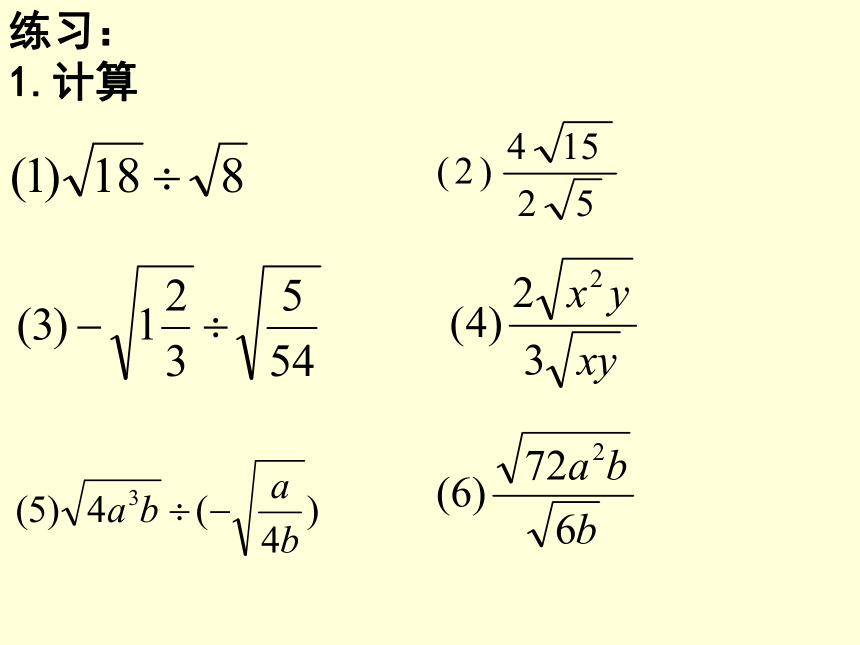

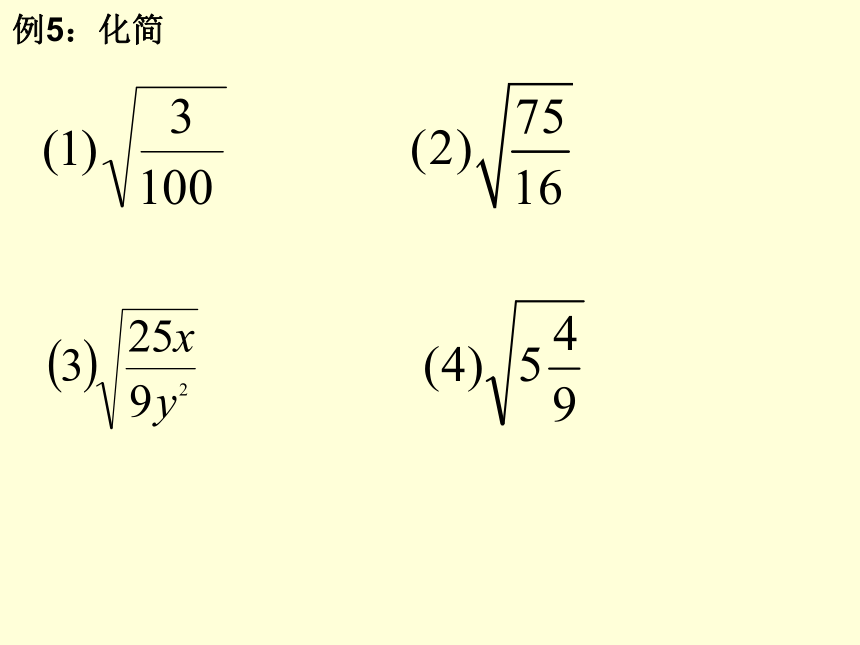
文档简介
第十六章 二次根式
16.2 第2课时 二次根式的除法
1
2
学习目标
掌握二次根式的除法;
学会把二次根式化简为被开方数中不含能开得尽方的因数或因式的最简二次根式.
a≥0,b≥0
1.二次根式的乘法:
复习提问
把开方开得尽的因数或因式,开方后移到根号外.
2.化简二次根式:
观察三组式子的结果,我们得到下面三个等式:
(1)
(2)
(3)
特殊
一般
a,b的取值范围需不需要注意?
语言叙述:
二次根式相除,把被开方数相除,根指数不变。
推广:
其中,a≥0,b>0,n≠0.
如果根号前有系数,就把系数相除,仍旧作为二次根号前的系数。
计算
练习:
1.计算
把 反过来,就得到
商的算术平方根的性质:
利用它可以进行二次根式的化简。
例5:化简
练习:
1.化简。
这样的二次根式,叫做最简二次根式。
知识要点
以上各例题的最后结果:
简记为:一根号无分母,分母无根号;二不能再开方.
分母中不含二次根式。
被开方数不能含有小数或分数。
分子分母不能约分。
最后结果中的二次根式要求化成最简二次根式。
在二次根式的运算中, 最后结果的一般要求
×
×
×
×
判断下列各式是否为最简二次根式?
√
指出下列各式中的最简二次根式
化简二次根式,需注意以下几点:
1.被开方数是带分数时要化成假分数;
2.被开方数是小数的要化成分数;
3.被开方数中含有能开方的因式时,要分解
因式并将能开方的因式开方。
根号含分母化简的一般步骤:
“一移”,即将分子、分母中能开得尽方的因数(式)移到根号外;
“二乘”,即将分子、分母同乘分母的有理化因数(式);
“三化”,即化简计算.
一题多解
为了去掉分母中的根号
最后结果的分母中不含二次根式。
(4)
为了去掉分母中的根号
最后结果的分母中不含二次根式。
拓展:二次根式混合运算
计算
几个二次根式相乘除,
将系数、被开方数分别相乘除。
课堂小结
二次根式除法
法则
性质
拓展法则:
相关概念
分母有理化
最简二次根式
16.2 第2课时 二次根式的除法
1
2
学习目标
掌握二次根式的除法;
学会把二次根式化简为被开方数中不含能开得尽方的因数或因式的最简二次根式.
a≥0,b≥0
1.二次根式的乘法:
复习提问
把开方开得尽的因数或因式,开方后移到根号外.
2.化简二次根式:
观察三组式子的结果,我们得到下面三个等式:
(1)
(2)
(3)
特殊
一般
a,b的取值范围需不需要注意?
语言叙述:
二次根式相除,把被开方数相除,根指数不变。
推广:
其中,a≥0,b>0,n≠0.
如果根号前有系数,就把系数相除,仍旧作为二次根号前的系数。
计算
练习:
1.计算
把 反过来,就得到
商的算术平方根的性质:
利用它可以进行二次根式的化简。
例5:化简
练习:
1.化简。
这样的二次根式,叫做最简二次根式。
知识要点
以上各例题的最后结果:
简记为:一根号无分母,分母无根号;二不能再开方.
分母中不含二次根式。
被开方数不能含有小数或分数。
分子分母不能约分。
最后结果中的二次根式要求化成最简二次根式。
在二次根式的运算中, 最后结果的一般要求
×
×
×
×
判断下列各式是否为最简二次根式?
√
指出下列各式中的最简二次根式
化简二次根式,需注意以下几点:
1.被开方数是带分数时要化成假分数;
2.被开方数是小数的要化成分数;
3.被开方数中含有能开方的因式时,要分解
因式并将能开方的因式开方。
根号含分母化简的一般步骤:
“一移”,即将分子、分母中能开得尽方的因数(式)移到根号外;
“二乘”,即将分子、分母同乘分母的有理化因数(式);
“三化”,即化简计算.
一题多解
为了去掉分母中的根号
最后结果的分母中不含二次根式。
(4)
为了去掉分母中的根号
最后结果的分母中不含二次根式。
拓展:二次根式混合运算
计算
几个二次根式相乘除,
将系数、被开方数分别相乘除。
课堂小结
二次根式除法
法则
性质
拓展法则:
相关概念
分母有理化
最简二次根式
