人教版数学九 年级下册28.1.2特殊角的三角函数值及用计算器求锐角三角函数值课件(共16张ppt)
文档属性
| 名称 | 人教版数学九 年级下册28.1.2特殊角的三角函数值及用计算器求锐角三角函数值课件(共16张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 00:00:00 | ||
图片预览



文档简介
第二十八章
28.1 锐角三角函数(3)
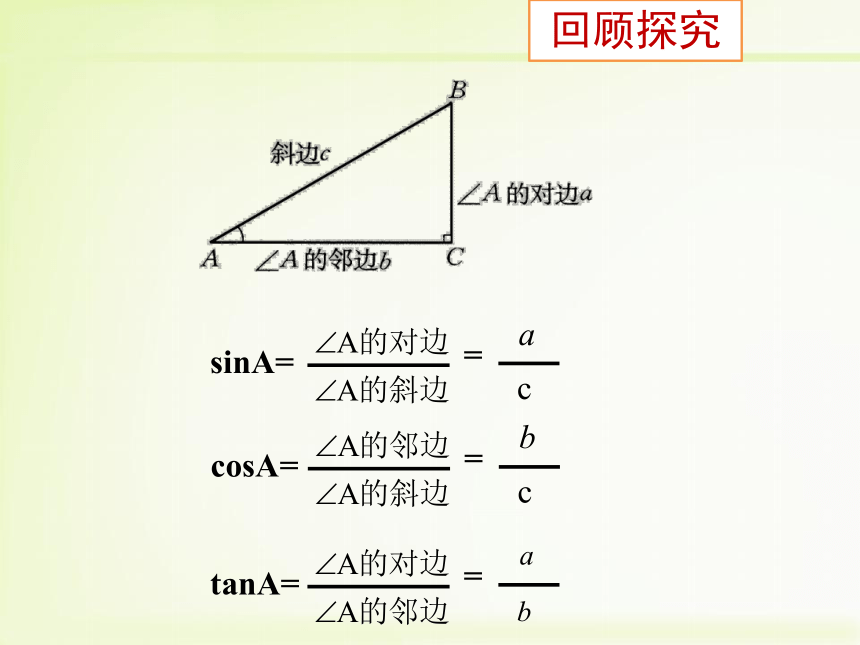
回顾探究
=
a
c
sinA=
=
b
c
cosA=
=
a
b
tanA=
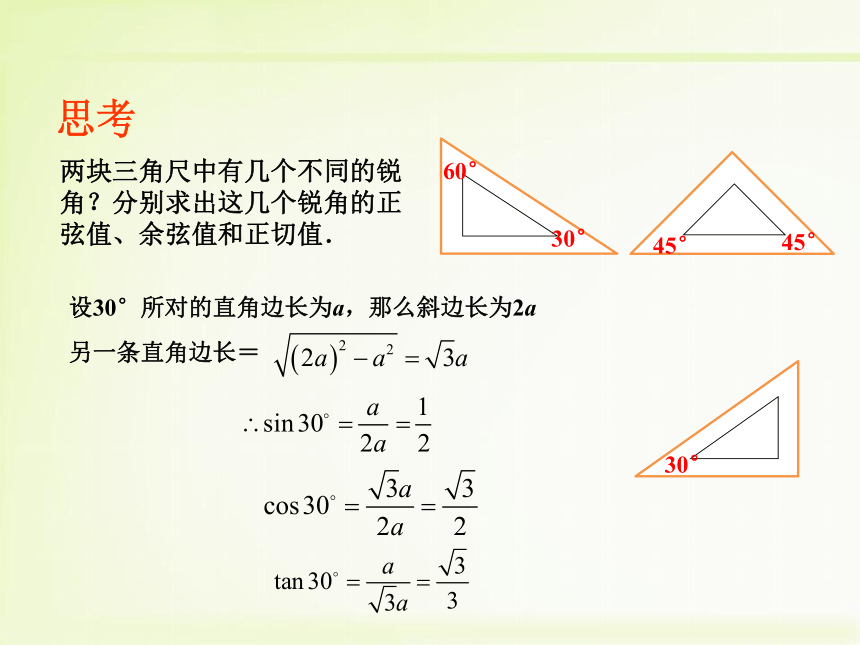
两块三角尺中有几个不同的锐角?分别求出这几个锐角的正弦值、余弦值和正切值.
设30°所对的直角边长为a,那么斜边长为2a
另一条直角边长=
30°
60°
45°
45°
30°
设两条直角边长为a,则斜边长=
60°
45°
锐角 A
锐角三角函数
30°
45°
60°
sin A
cos A
tan A
1
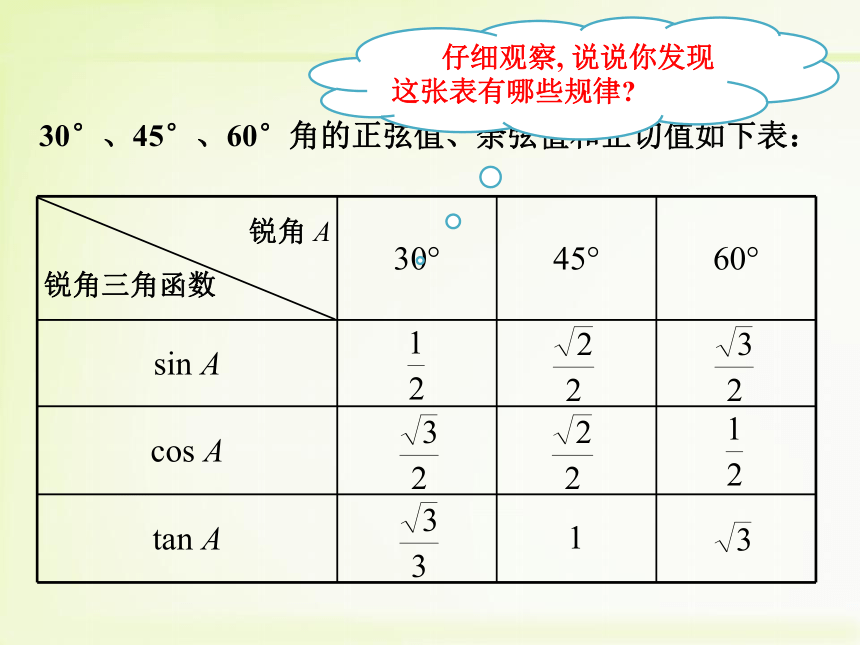
30°、45°、60°角的正弦值、余弦值和正切值如下表:
仔细观察, 说说你发现这张表有哪些规律?
例3 求下列各式的值:
(1)cos260°+sin260°
(2)
解: (1) cos260°+sin260°
=1
(2)
=0
例题探究
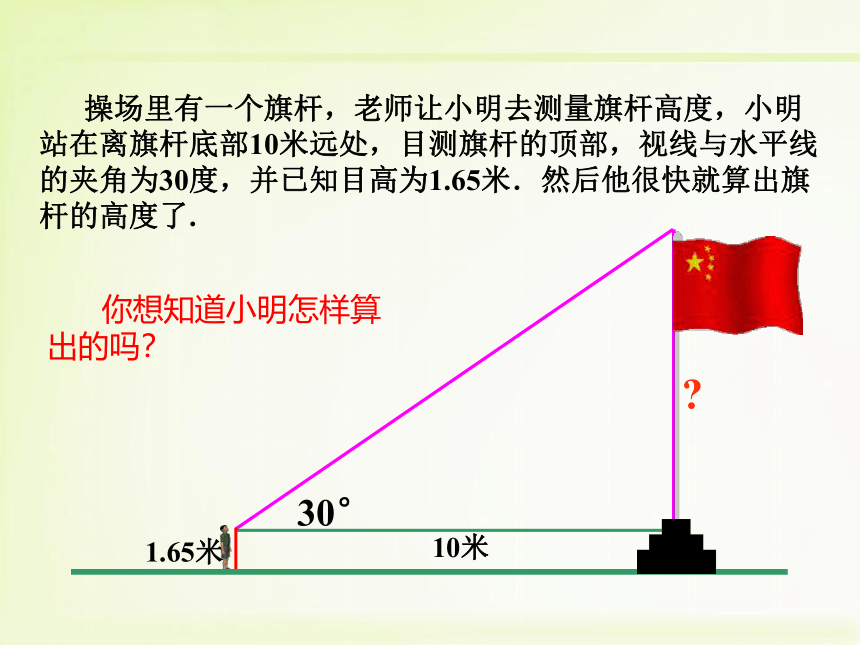
操场里有一个旗杆,老师让小明去测量旗杆高度,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为30度,并已知目高为1.65米.然后他很快就算出旗杆的高度了.
1.65米
10米
?
你想知道小明怎样算出的吗?
30°
例4、(1)如图,在Rt△ABC中,∠C=90°,AB= , BC= . 求∠A的度数.
(2)如图,已知圆锥的高AO等于圆锥的底面半径OB的 倍, 求α.
(1)
(2)
1. 如图,在Rt△ABC中,∠ACB=90度,CD⊥AB于D ,已知∠B=30度,计算 的值.
D
A
B
C
做一做
2. 如图,在△ABC中,∠A=30度,
求AB.
A
B
C
D
解:过点C作CD⊥AB于点D
∠A=30度,
求下列各式的值:
(1)1-2 sin30°cos30°
(2)3tan30°-tan45°+2sin60°
(3)
解:
(1)1-2 sin30°cos30°
(2)3tan30°-tan45°+2sin60°
课堂练习
2. 在Rt△ABC中,∠C=90°,
求∠A、∠B的度数.
B
A
C
解: 由勾股定理
∴ ∠A=30°
∠B = 90°- ∠ A = 90°-30°= 60°
1、已知:α为锐角,且满足
,求α的度数.
2、在Rt△ABC中,∠C=90°,化简
我们今天学习了哪些知识?
课堂小结
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角a
三角函数
30°
45°
60°
sin a
cos a
tan a
对于sinα与tanα,角度越大,函数值也越大;(带正)
对于cosα,角度越大,函数值越小.
28.1 锐角三角函数(3)
回顾探究
=
a
c
sinA=
=
b
c
cosA=
=
a
b
tanA=
两块三角尺中有几个不同的锐角?分别求出这几个锐角的正弦值、余弦值和正切值.
设30°所对的直角边长为a,那么斜边长为2a
另一条直角边长=
30°
60°
45°
45°
30°
设两条直角边长为a,则斜边长=
60°
45°
锐角 A
锐角三角函数
30°
45°
60°
sin A
cos A
tan A
1
30°、45°、60°角的正弦值、余弦值和正切值如下表:
仔细观察, 说说你发现这张表有哪些规律?
例3 求下列各式的值:
(1)cos260°+sin260°
(2)
解: (1) cos260°+sin260°
=1
(2)
=0
例题探究
操场里有一个旗杆,老师让小明去测量旗杆高度,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为30度,并已知目高为1.65米.然后他很快就算出旗杆的高度了.
1.65米
10米
?
你想知道小明怎样算出的吗?
30°
例4、(1)如图,在Rt△ABC中,∠C=90°,AB= , BC= . 求∠A的度数.
(2)如图,已知圆锥的高AO等于圆锥的底面半径OB的 倍, 求α.
(1)
(2)
1. 如图,在Rt△ABC中,∠ACB=90度,CD⊥AB于D ,已知∠B=30度,计算 的值.
D
A
B
C
做一做
2. 如图,在△ABC中,∠A=30度,
求AB.
A
B
C
D
解:过点C作CD⊥AB于点D
∠A=30度,
求下列各式的值:
(1)1-2 sin30°cos30°
(2)3tan30°-tan45°+2sin60°
(3)
解:
(1)1-2 sin30°cos30°
(2)3tan30°-tan45°+2sin60°
课堂练习
2. 在Rt△ABC中,∠C=90°,
求∠A、∠B的度数.
B
A
C
解: 由勾股定理
∴ ∠A=30°
∠B = 90°- ∠ A = 90°-30°= 60°
1、已知:α为锐角,且满足
,求α的度数.
2、在Rt△ABC中,∠C=90°,化简
我们今天学习了哪些知识?
课堂小结
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角a
三角函数
30°
45°
60°
sin a
cos a
tan a
对于sinα与tanα,角度越大,函数值也越大;(带正)
对于cosα,角度越大,函数值越小.
