人教版数学九年级下册课件:27.2.1相似三角形的判定(21张PPT)
文档属性
| 名称 | 人教版数学九年级下册课件:27.2.1相似三角形的判定(21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 308.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 00:00:00 | ||
图片预览




文档简介
第二十七章相似
相似三角形的判定
第2课时
1.理解三角形相似的两个判定定理.
2.能够运用三角形相似的两个判定定理进行推理论证和计算.
学习目标
1.三角形全等有哪些简便的判定方法?
SSS,SAS,ASA,AAS
2.直角三角形全等特有的判定方法是什么?
HL
3.全等是相似比为1的特殊情形,类比三角形全等的判定,判定两个三角形相似是否也有简便的方法?试着猜想一下?
类比猜想
猜想:
(1)三边成比例的两个三角形相似;
(2)两边成比例且夹角相等的两个三角形相似;
(3)两角分别相等的两个三角形相似;
(4)斜边和一条直角边成比例的两个直角三角形相似.
类比猜想
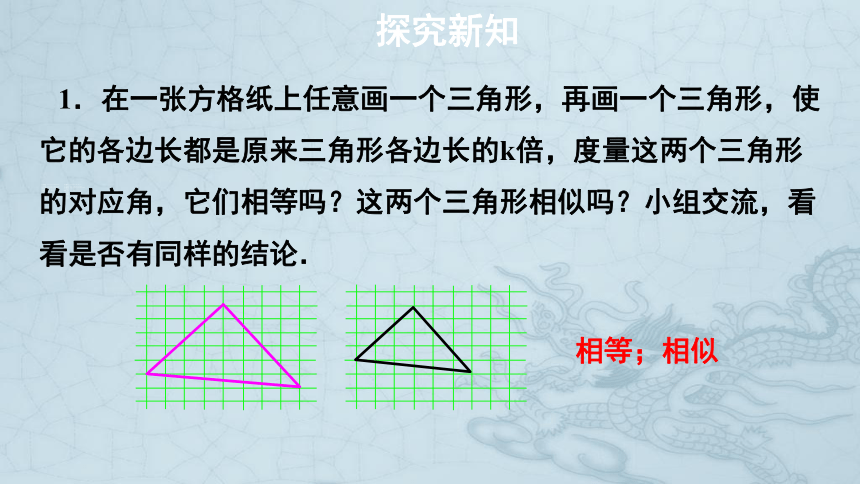
1.在一张方格纸上任意画一个三角形,再画一个三角形,使它的各边长都是原来三角形各边长的k倍,度量这两个三角形的对应角,它们相等吗?这两个三角形相似吗?小组交流,看看是否有同样的结论.
相等;相似
探究新知
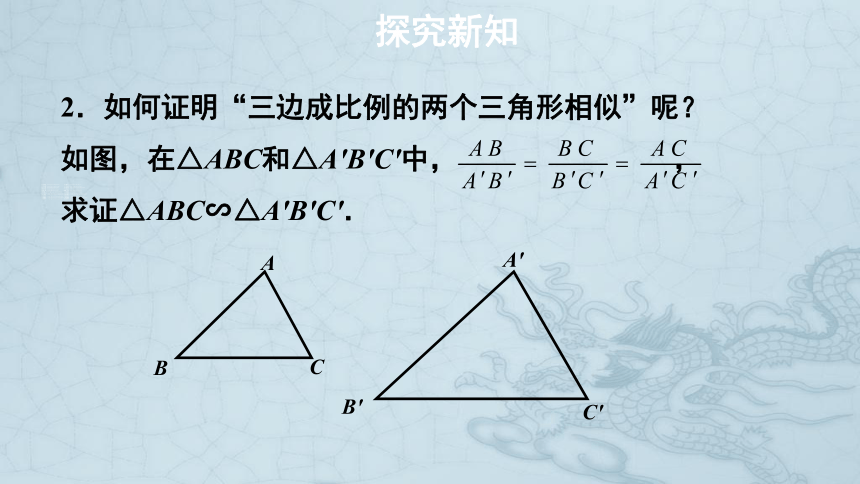
2.如何证明“三边成比例的两个三角形相似”呢?
如图,在△ABC和△A'B'C'中, ,
求证△ABC∽△A'B'C'.
A
B
C
A'
B'
C'
探究新知
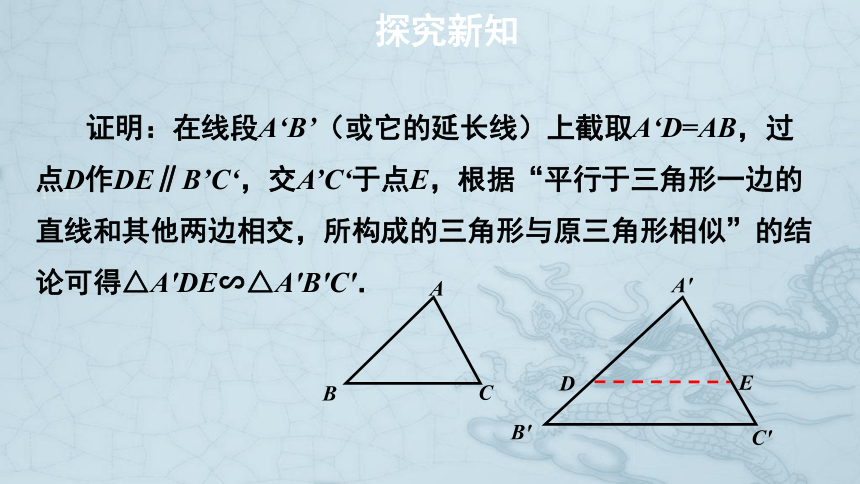
证明:在线段A‘B’(或它的延长线)上截取A‘D=AB,过点D作DE∥B’C‘,交A’C‘于点E,根据“平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似”的结论可得△A'DE∽△A'B'C'.
A
B
C
A'
B'
C'
D
E
探究新知
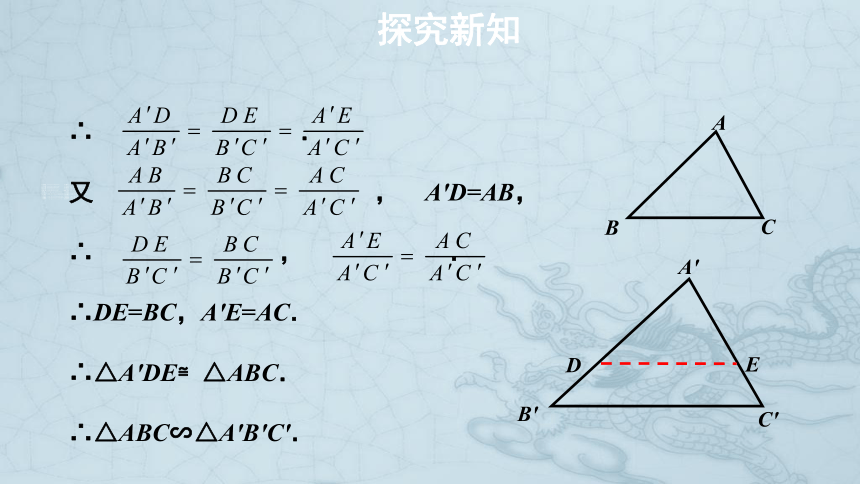
∴ .
又 , A'D=AB,
∴ , .
∴DE=BC,A'E=AC.
∴△A'DE≌△ABC.
∴△ABC∽△A'B'C'.
A
B
C
A'
B'
C'
D
E
探究新知
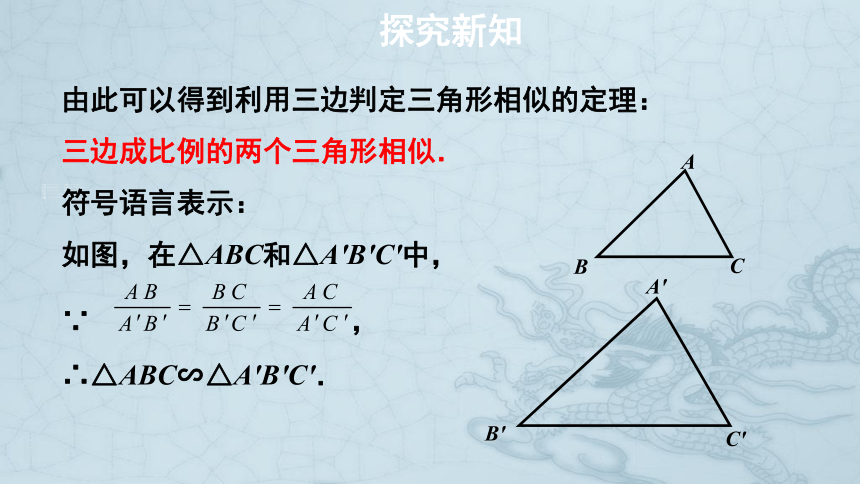
由此可以得到利用三边判定三角形相似的定理:
三边成比例的两个三角形相似.
符号语言表示:
如图,在△ABC和△A'B'C'中,
∵ ,
∴△ABC∽△A'B'C'.
A
B
C
A'
B'
C'
探究新知
3.类比判定三角形全等的“SAS”方法,以及“三边成比例的两个三角形相似”的证明思路,
A
B
C
A'
B'
C'
证明:在线段A'B'(或它的延长线)上截取A'D=AB,
过点D作DE∥B'C',交A'C'于点E,
可以得到△ADE∽△A
∴
D
E
∵
探究新知
探究新知
∴
∴△A'DE≌△ABC.
∴△ABC∽△A'B'C'.
,
∴
∵∠A=∠
A
B
C
A'
B'
C'
D
E
由此可得:两边成比例且夹角相等的两个三角形相似.
探究新知
如图,在△ABC和△A'B'C'中,
∵ ,∠A=∠A',
∴△ABC∽△A'B'C'.
符号语言表示:
例1 根据下列条件,判断△ABC与△A'B'C'是否
相似,并说明理由:
(1)AB=4 cm,BC=6 cm,AC=8 cm,
A'B'=12 cm,B'C'=18 cm,A'C'=24 cm;
(2)∠A=120°,AB=7 cm,AC=14 cm,
∠A'=120°,A'B'=3 cm,A'C'=6 cm.
例题解析
解:(1)∵
,
∴△ABC∽△A'B'C'.
∴
.
,
,
例题解析
(2)∵
,
∴△ABC∽△A'B'C'.
∴
.
,
又∠A=∠A',
例题解析
例2. 如图,点E在AB上,CE//BD,BE=3EC,BD=3EA,
求证:△BDE∽△EAC.
B
E
A
C
D
证明:∵CE//BD
∴∠CEA=∠B
∴ △BDE∽△EAC.
∴
例题解析
∵BE=3EC,BD=3EA
1.如图,在四边形ABCD中,∠B=∠ACD,
AB=6,BC=4,AC=5,CD= ,则AD= .
B
C
A
D
课堂练习
2.不等长的两条对角线AC、BD相较于点O,且将四边形
ABCD分成甲、乙、丙丁四个三角形.若OA:OC=OB:OD,则
甲、乙、丙、丁这4个三角形中,一定相似的有_______.
甲和丙
解∵OA:OC=OB:OD
∴
∵ ∠AOB=∠COD
可得甲和丙相似.
C
A
B
D
甲
乙
丙
丁
课堂练习
3.已知:如图,在△ABC中,∠ C=90°,D,E分别是AB、AC
上的两点,并且
.猜想:ED与AB有什么
位置关系?并说明理由.
C
B
A
D
E
且∠A=∠A,
所以△ADE∽△ACB,
所以∠ADE=∠C=90°
解:ED⊥AB
∵
∴
课堂练习
三角形相似的判定方法:
1.通过定义(比较复杂,烦琐);
2.平行于三角形一边的直线和其他两边相交,所构成的三角形
与原三角形相似(只能在特定的图形里面使用);
3.三边对应成比例(SSS);
4.两边对应成比例且夹角相等(SAS);
课堂小结
再见
相似三角形的判定
第2课时
1.理解三角形相似的两个判定定理.
2.能够运用三角形相似的两个判定定理进行推理论证和计算.
学习目标
1.三角形全等有哪些简便的判定方法?
SSS,SAS,ASA,AAS
2.直角三角形全等特有的判定方法是什么?
HL
3.全等是相似比为1的特殊情形,类比三角形全等的判定,判定两个三角形相似是否也有简便的方法?试着猜想一下?
类比猜想
猜想:
(1)三边成比例的两个三角形相似;
(2)两边成比例且夹角相等的两个三角形相似;
(3)两角分别相等的两个三角形相似;
(4)斜边和一条直角边成比例的两个直角三角形相似.
类比猜想
1.在一张方格纸上任意画一个三角形,再画一个三角形,使它的各边长都是原来三角形各边长的k倍,度量这两个三角形的对应角,它们相等吗?这两个三角形相似吗?小组交流,看看是否有同样的结论.
相等;相似
探究新知
2.如何证明“三边成比例的两个三角形相似”呢?
如图,在△ABC和△A'B'C'中, ,
求证△ABC∽△A'B'C'.
A
B
C
A'
B'
C'
探究新知
证明:在线段A‘B’(或它的延长线)上截取A‘D=AB,过点D作DE∥B’C‘,交A’C‘于点E,根据“平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似”的结论可得△A'DE∽△A'B'C'.
A
B
C
A'
B'
C'
D
E
探究新知
∴ .
又 , A'D=AB,
∴ , .
∴DE=BC,A'E=AC.
∴△A'DE≌△ABC.
∴△ABC∽△A'B'C'.
A
B
C
A'
B'
C'
D
E
探究新知
由此可以得到利用三边判定三角形相似的定理:
三边成比例的两个三角形相似.
符号语言表示:
如图,在△ABC和△A'B'C'中,
∵ ,
∴△ABC∽△A'B'C'.
A
B
C
A'
B'
C'
探究新知
3.类比判定三角形全等的“SAS”方法,以及“三边成比例的两个三角形相似”的证明思路,
A
B
C
A'
B'
C'
证明:在线段A'B'(或它的延长线)上截取A'D=AB,
过点D作DE∥B'C',交A'C'于点E,
可以得到△ADE∽△A
∴
D
E
∵
探究新知
探究新知
∴
∴△A'DE≌△ABC.
∴△ABC∽△A'B'C'.
,
∴
∵∠A=∠
A
B
C
A'
B'
C'
D
E
由此可得:两边成比例且夹角相等的两个三角形相似.
探究新知
如图,在△ABC和△A'B'C'中,
∵ ,∠A=∠A',
∴△ABC∽△A'B'C'.
符号语言表示:
例1 根据下列条件,判断△ABC与△A'B'C'是否
相似,并说明理由:
(1)AB=4 cm,BC=6 cm,AC=8 cm,
A'B'=12 cm,B'C'=18 cm,A'C'=24 cm;
(2)∠A=120°,AB=7 cm,AC=14 cm,
∠A'=120°,A'B'=3 cm,A'C'=6 cm.
例题解析
解:(1)∵
,
∴△ABC∽△A'B'C'.
∴
.
,
,
例题解析
(2)∵
,
∴△ABC∽△A'B'C'.
∴
.
,
又∠A=∠A',
例题解析
例2. 如图,点E在AB上,CE//BD,BE=3EC,BD=3EA,
求证:△BDE∽△EAC.
B
E
A
C
D
证明:∵CE//BD
∴∠CEA=∠B
∴ △BDE∽△EAC.
∴
例题解析
∵BE=3EC,BD=3EA
1.如图,在四边形ABCD中,∠B=∠ACD,
AB=6,BC=4,AC=5,CD= ,则AD= .
B
C
A
D
课堂练习
2.不等长的两条对角线AC、BD相较于点O,且将四边形
ABCD分成甲、乙、丙丁四个三角形.若OA:OC=OB:OD,则
甲、乙、丙、丁这4个三角形中,一定相似的有_______.
甲和丙
解∵OA:OC=OB:OD
∴
∵ ∠AOB=∠COD
可得甲和丙相似.
C
A
B
D
甲
乙
丙
丁
课堂练习
3.已知:如图,在△ABC中,∠ C=90°,D,E分别是AB、AC
上的两点,并且
.猜想:ED与AB有什么
位置关系?并说明理由.
C
B
A
D
E
且∠A=∠A,
所以△ADE∽△ACB,
所以∠ADE=∠C=90°
解:ED⊥AB
∵
∴
课堂练习
三角形相似的判定方法:
1.通过定义(比较复杂,烦琐);
2.平行于三角形一边的直线和其他两边相交,所构成的三角形
与原三角形相似(只能在特定的图形里面使用);
3.三边对应成比例(SSS);
4.两边对应成比例且夹角相等(SAS);
课堂小结
再见
