人教版数学九年级下册课件27.1图形的相似(23张)
文档属性
| 名称 | 人教版数学九年级下册课件27.1图形的相似(23张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 681.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 17:52:50 | ||
图片预览







文档简介
第二十七章 相似
图形的相似
中学数学精品课件
1.理解相似图形的概念.
2.理解相似多边形的概念、性质和判定,并运用其性质
和判定解决实际问题.
学习目标
相似图形
相似图形
相似图形
相似图形
下面这些图形有什么共同特征?
探究新知
相似图形:我们把这种形状相同的图形说成是相似图形.
共同特征:形状相同.
探究新知
问题2 举出现实生活中的几个相似图形的例子.
问题1 两个图形相似,其中一个图形可以看作由另一个图形_______或______得到的.
放大
缩小
例如,放映电影时,投在屏幕上的画面就是胶片上的图形的放大;
实际的建筑物和它的模型是相似的;
用复印机把一个图形放大或缩小所得的图形,也都与原来的图形相似.
探究新知
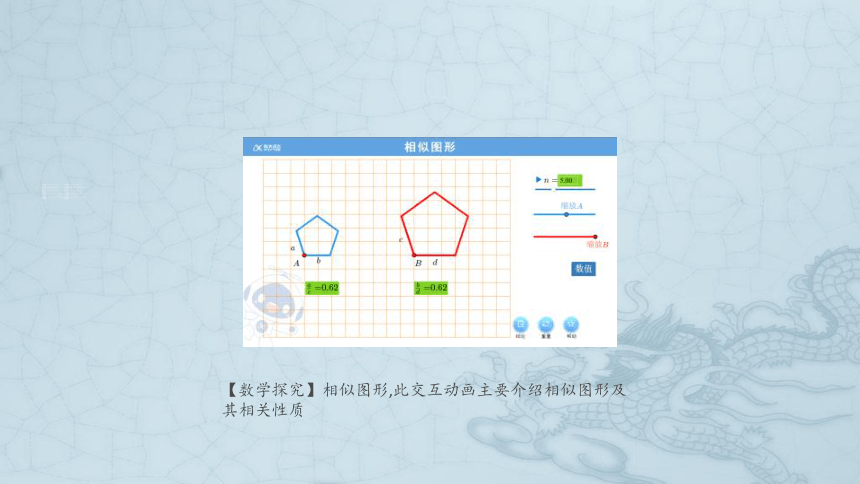
【数学探究】相似图形,此交互动画主要介绍相似图形及其相关性质
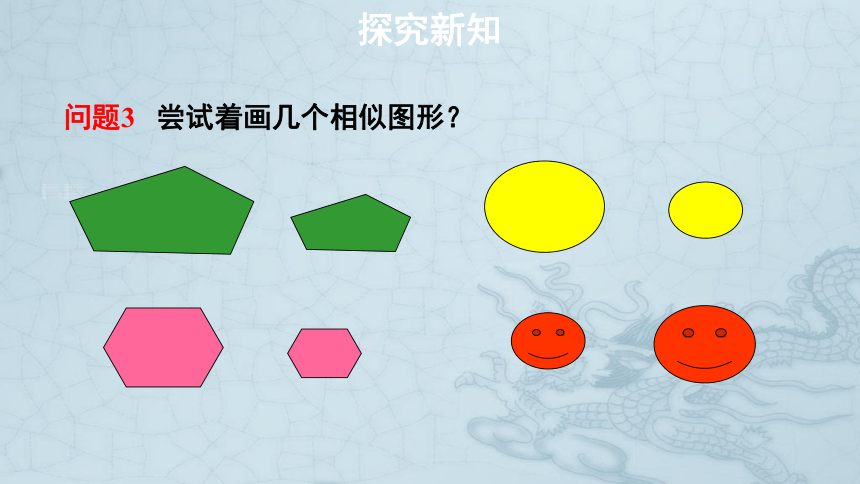
问题3 尝试着画几个相似图形?
探究新知
五星红旗上大五角星和四颗小五角星是相似图形,而四颗小五角星是全等图形.
全等是相似的特例.
探究新知
相似多边形的定义:
两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形.
相似多边形对应边的比叫做相似比.
相似比为1时,相似的两个图形有什么关系呢?
相似比为1时,两图形全等.
探究新知
∴四边形ABCD与四边形相似.
几何语言表示(以四边形为例):
如图,在四边形ABCD和四边形 中,
,
,
,
,
,
A
B
C
D
探究新知
线段成比例
对于四条线段a,b,c,d,如果其中两条线段的
比(即它们长度的比)与另两条线段的比相等,
如
,(即ad=bc)我们就说这四条线段成比例.
探究新知
两个大小不同的正方形相似吗?为什么?
两个大小不同的正方形是相似的,因为它们的角分别相等,边成比例.
归纳:边数相同的正多边形都相似.
探究新知
在正三角形ABC与正三角形DEF中,
可以得到
∠A=∠D=60?,∠B=∠E=60?,∠C=∠F=60?,
.
相似多边形的性质:
相似多边形的对应角相等,对应边成比例.
C
A
B
D
E
F
探究新知
相似多边形的判定:
相似多边形的定义既是性质又是判定,即对应角相等,
对应边成比例的多边形是相似多边形.
探究新知
例1. 如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x.
解:因为四边形ABCD和EFGH相似,所以它们的对应角相等.由此可得
α=∠C=83°,∠A=∠E=118°.
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
例题解析
因为四边形ABCD和EFGH相似,所以它们的对应边成比例,由此可得
解得 x=28.
在四边形ABCD中,
β=360°-(78°+83°+118°)=81°.
.
,即
例题解析
例2.如图所示的两个五边形相似,求a、b、c、d的值.
解:由图示可知两个图形的相似比为
.
解得a=3,b=4.5,c=4,d=6.
例题解析
1.图中是人们从平面镜及哈哈镜里看到的不同镜像,
它们相似吗?
2.如图,从放大镜里看到的三角尺和原来的三角尺相似吗?
课堂练习
3.如图所示的两个三角形相似吗?为什么?
4.下列各组数中,成比例的是( ).
A.-7,-5,14,5 B.-6,-8,3,4
C.3,5,9,12 D.2,3,6,12
课堂练习
解:相似,由已知条件可知它们的角分别相等,边成比例.
B
5.如果
,那么
等于( ).
6.下列说法中,错误的是( ).
A.两个全等三角形一定是相似形
B.两个等腰三角形一定相似
C.两个等边三角形一定相似
D.两个等腰直角三角形一定相似
C.
A.
B.
D.
课堂练习
D
B
7.在比例尺为1︰10 000 000的地图上,量得甲、乙两地的距离是30 cm,求两地的实际距离.
解:设两地的实际距离为x cm,则
.
解得x=300 000 000.
300 000 000 cm=3 000 km.
答:甲,乙两地的实际距离是3000km.
课堂练习
1.相似图形的概念
形状相同的图形叫做相似图形.
2.相似多边形的概念和相似比
两个边数相同的多边形,如果它们的角分别相等,
边成比例,那么这两个多边形叫做相似多边形.
相似多边形对应边的比叫做相似比.
3.相似多边形的性质
相似多边形的对应角相等,对应边成比例.
课堂小结
再见
图形的相似
中学数学精品课件
1.理解相似图形的概念.
2.理解相似多边形的概念、性质和判定,并运用其性质
和判定解决实际问题.
学习目标
相似图形
相似图形
相似图形
相似图形
下面这些图形有什么共同特征?
探究新知
相似图形:我们把这种形状相同的图形说成是相似图形.
共同特征:形状相同.
探究新知
问题2 举出现实生活中的几个相似图形的例子.
问题1 两个图形相似,其中一个图形可以看作由另一个图形_______或______得到的.
放大
缩小
例如,放映电影时,投在屏幕上的画面就是胶片上的图形的放大;
实际的建筑物和它的模型是相似的;
用复印机把一个图形放大或缩小所得的图形,也都与原来的图形相似.
探究新知
【数学探究】相似图形,此交互动画主要介绍相似图形及其相关性质
问题3 尝试着画几个相似图形?
探究新知
五星红旗上大五角星和四颗小五角星是相似图形,而四颗小五角星是全等图形.
全等是相似的特例.
探究新知
相似多边形的定义:
两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形.
相似多边形对应边的比叫做相似比.
相似比为1时,相似的两个图形有什么关系呢?
相似比为1时,两图形全等.
探究新知
∴四边形ABCD与四边形相似.
几何语言表示(以四边形为例):
如图,在四边形ABCD和四边形 中,
,
,
,
,
,
A
B
C
D
探究新知
线段成比例
对于四条线段a,b,c,d,如果其中两条线段的
比(即它们长度的比)与另两条线段的比相等,
如
,(即ad=bc)我们就说这四条线段成比例.
探究新知
两个大小不同的正方形相似吗?为什么?
两个大小不同的正方形是相似的,因为它们的角分别相等,边成比例.
归纳:边数相同的正多边形都相似.
探究新知
在正三角形ABC与正三角形DEF中,
可以得到
∠A=∠D=60?,∠B=∠E=60?,∠C=∠F=60?,
.
相似多边形的性质:
相似多边形的对应角相等,对应边成比例.
C
A
B
D
E
F
探究新知
相似多边形的判定:
相似多边形的定义既是性质又是判定,即对应角相等,
对应边成比例的多边形是相似多边形.
探究新知
例1. 如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x.
解:因为四边形ABCD和EFGH相似,所以它们的对应角相等.由此可得
α=∠C=83°,∠A=∠E=118°.
D
A
B
C
18
21
78°
83°
β
24
G
E
F
H
α
x
118°
例题解析
因为四边形ABCD和EFGH相似,所以它们的对应边成比例,由此可得
解得 x=28.
在四边形ABCD中,
β=360°-(78°+83°+118°)=81°.
.
,即
例题解析
例2.如图所示的两个五边形相似,求a、b、c、d的值.
解:由图示可知两个图形的相似比为
.
解得a=3,b=4.5,c=4,d=6.
例题解析
1.图中是人们从平面镜及哈哈镜里看到的不同镜像,
它们相似吗?
2.如图,从放大镜里看到的三角尺和原来的三角尺相似吗?
课堂练习
3.如图所示的两个三角形相似吗?为什么?
4.下列各组数中,成比例的是( ).
A.-7,-5,14,5 B.-6,-8,3,4
C.3,5,9,12 D.2,3,6,12
课堂练习
解:相似,由已知条件可知它们的角分别相等,边成比例.
B
5.如果
,那么
等于( ).
6.下列说法中,错误的是( ).
A.两个全等三角形一定是相似形
B.两个等腰三角形一定相似
C.两个等边三角形一定相似
D.两个等腰直角三角形一定相似
C.
A.
B.
D.
课堂练习
D
B
7.在比例尺为1︰10 000 000的地图上,量得甲、乙两地的距离是30 cm,求两地的实际距离.
解:设两地的实际距离为x cm,则
.
解得x=300 000 000.
300 000 000 cm=3 000 km.
答:甲,乙两地的实际距离是3000km.
课堂练习
1.相似图形的概念
形状相同的图形叫做相似图形.
2.相似多边形的概念和相似比
两个边数相同的多边形,如果它们的角分别相等,
边成比例,那么这两个多边形叫做相似多边形.
相似多边形对应边的比叫做相似比.
3.相似多边形的性质
相似多边形的对应角相等,对应边成比例.
课堂小结
再见
