6.3反比例函数的应用-北师大版九年级数学上册假期同步测试(含答案)
文档属性
| 名称 | 6.3反比例函数的应用-北师大版九年级数学上册假期同步测试(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 201.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 00:00:00 | ||
图片预览




文档简介
1052830012382500北师大版九年级数学上册第六章
6.3反比例函数的应用 同步测试
一.选择题
1.一司机驾驶汽车从甲地去乙地,他以80千米/时的平均速度用了6小时到达目的地,当他按原路匀速返回时,汽车的速度v(千米/时)与时间t(小时)的函数关系为( )
A.v= B.v+t=480 C.v= D.v=
2.如图,⊙O的半径为2,双曲线的解析式分别为false和false,则阴影部分的面积为( )
A. false B. false C. false D. false
3.今年,某公司推出一款新手机深受消费者推崇,但价格不菲.为此,某电子商城推出分期付款购买手机的活动,一部售价为9688元的新手机,前期付款3000元,后期每个月分别付相同的数额,则每个月付款额y(元)与付款月数x(x为正整数)之间的函数关系式是( )
A. B. C. D.
4.(2020?宁夏)如图,函数y1=x+1与函数y2=的图象相交于点M(1,m),N(﹣2,n).若y1>y2,则x的取值范围是( )
A.x<﹣2或0<x<1 B.x<﹣2或x>1
C.﹣2<x<0或0<x<1 D.﹣2<x<0或x>1
5.今年,某公司推出一款的新手机深受消费者推崇,但价格不菲.为此,某电子商城推出分期付款购买新手机的活动,一部售价为9688元的新手机,前期付款2000元,后期每个月分别付相同的数额,则每个月的付款额y(元)与付款月数x(x为正整数)之间的函数关系式是( )
A.y=+2000 B.y=﹣2000 C.y= D.y=
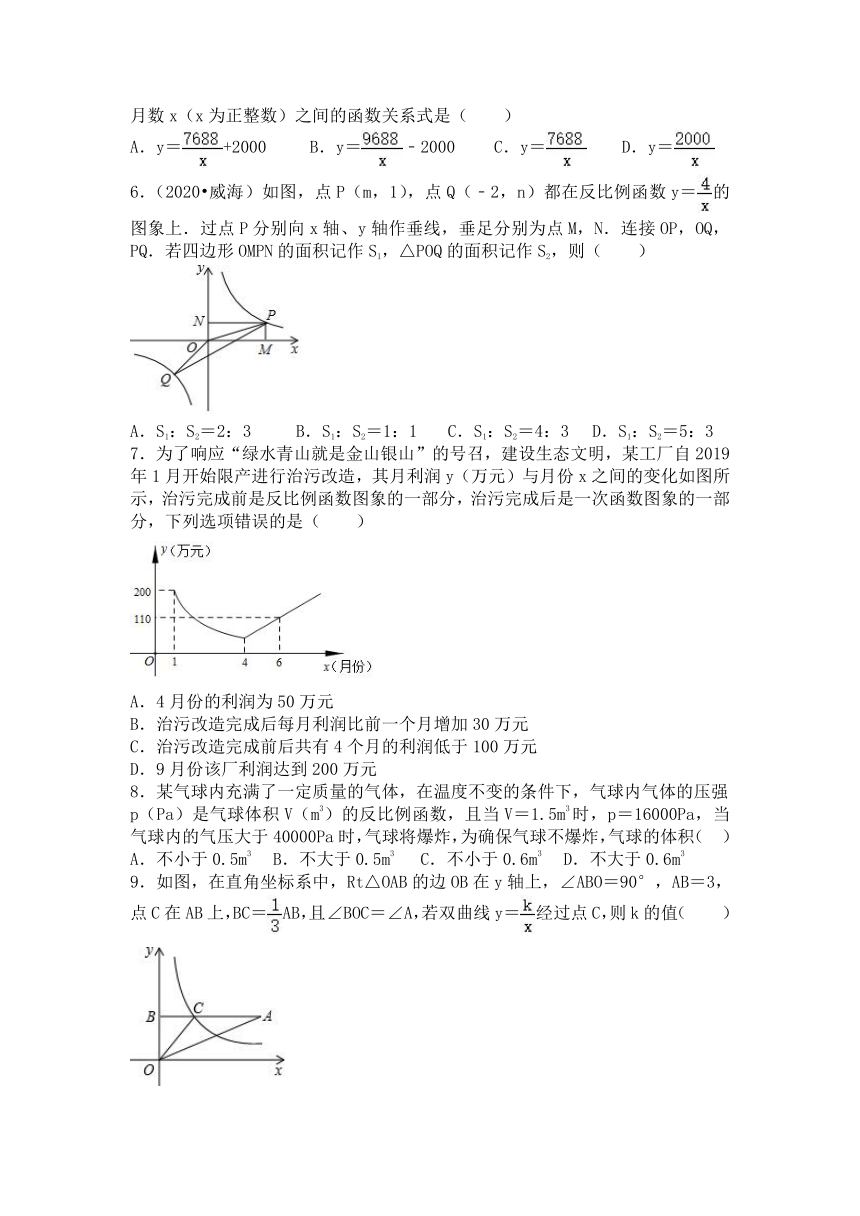
6.(2020?威海)如图,点P(m,1),点Q(﹣2,n)都在反比例函数y=的图象上.过点P分别向x轴、y轴作垂线,垂足分别为点M,N.连接OP,OQ,PQ.若四边形OMPN的面积记作S1,△POQ的面积记作S2,则( )
A.S1:S2=2:3 B.S1:S2=1:1 C.S1:S2=4:3 D.S1:S2=5:3
7.为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2019年1月开始限产进行治污改造,其月利润y(万元)与月份x之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分,下列选项错误的是( )
A.4月份的利润为50万元
B.治污改造完成后每月利润比前一个月增加30万元
C.治污改造完成前后共有4个月的利润低于100万元
D.9月份该厂利润达到200万元
8.某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强p(Pa)是气球体积V(m3)的反比例函数,且当V=1.5m3时,p=16000Pa,当气球内的气压大于40000Pa时,气球将爆炸,为确保气球不爆炸,气球的体积( )
A.不小于0.5m3 B.不大于0.5m3 C.不小于0.6m3 D.不大于0.6m3
9.如图,在直角坐标系中,Rt△OAB的边OB在y轴上,∠ABO=90°,AB=3,点C在AB上,BC=AB,且∠BOC=∠A,若双曲线y=经过点C,则k的值( )
A. B. C.1 D.2
10.如图,A、B是函数y=(x>0)上两点,点P在第一象限,且在函数y=(x>0)下方,作PB⊥x轴,PA⊥y轴,下列说法正确的是( )
①△AOP≌△BOP; ②S△AOP=S△BOP;
③若OA=OB,则OP平分∠AOB; ④若S△BOP=2,则S△ABP=6.
A.1个 B.2个 C.3个 D.4个
二.填空题
11.若一个三角形的面积是8false 则其底边长y(cm) 与这边上的高x(cm)之间的关系是__________.
12.如图所示,小华设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,在中点O右侧用一个弹簧秤向下拉,改变弹簧秤与点O的距离x(cm),观察弹簧秤的示数y(N)的变化情况.实验数据记录如下:
x(cm)…10
15
20
25 30…
y(N)…30
20
15
12 10…
猜测y与x之间的函数关系,并求出函数关系式为 .
13.反比例函数false的图象上有一点P(2,n),将点P向右平移1个单位,再向下平移1个单位得到点Q.若点Q也在该函数的图象上,则k= .
14.有x个小朋友平均分20个苹果,每人分得的苹果y(每人每个)与x(个)之间的函数关系式为 .
15.老王要把一篇24000字的社会调查报告录入电脑,则其录入的时间t(分)与录入文字的平均速度v(字/分)之间的函数表达式应为t= (v>0).
16.李老师参加了某电脑公司推出的分期付款(无利息)购买电脑活动,他购买的电脑价格为9800元,交了首付之后每月付款y元,x个月结清余款,y与x满足如图的函数解析式,通过以上信息可知李老师的首付款为________.
17.如图,点P(a,a)是反比例函数在第一象限内的图象上的一个点,以点P为顶点作等边△PAB,使A、B落在x轴上(点A在点B左侧),则△POA的面积是 .
18.如图是8个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作Tm(m为1~8的整数).函数y=(x<0)的图象为曲线L.
(1)若L过点T1,则k= ;
(2)若L过点T4,则它必定还过另一点Tm,则m= ;
(3)若曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,则k的整数值有 个.
三.解答题
19.方方驾驶小汽车匀速地从A地行驶到B地,行驶里程为480千米,设小汽车的行驶时间为t(单位:小时),行驶速股为v(单位:千米/小时),且全程速度限定为不超过120千米/小时.
求v关于t的函数表达式.
(2)方方上午8点驾驶小汽车从A地出发.
①方方需在当天12点48分至14点(含12点48分和14点)间到达B地.求小汽车行驶速度v的范围.
②方方能否在当天11点30分前到达B地?说明理由.
20.小亮在研究矩形的面积S与矩形的边长x,y之间的关系时,得到如表数据:
x
0.5
1
1.5
2
3
4
6
12
y
12
6
■
3
2
1.5
1
0.5
结果发现一个数据被墨水涂黑了,
(1)被墨水涂黑的数据为 ;
(2)y与x的函数关系式为 ,且y随x的增大而 ;
(3)如图是小亮画出的y关于x的函数图象,点B、E均在该函数的图象上,其中矩形OABC的面积记为S1,矩形ODEF的面积记为S2,请判断S1与S2的大小关系,并说明理由;
(4)在(3)的条件下,DE交BC于点G,反比例函数y=的图象经过点G交AB于点H,连接OG、OH,则四边形OGBH的面积为 .
21.(2020?鞍山)如图,在平面直角坐标系中,一次函数y=x+1的图象与x轴,y轴的交点分别为点A,点B,与反比例函数y=(k≠0)的图象交于C,D两点,CE⊥x轴于点E,连接DE,AC=3.
(1)求反比例函数的解析式;
(2)求△CDE的面积.
22.某气球内充满了一定量的气体,当温度不变时,气球内气体的压强P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
(1)求这个反比例函数的表达式;
(2)当气球内的体积为气体1.6m3时,求气体压强P的值;
(3)当气球内的气体压强大于150kPa时,气球将爆炸,为了安全起见,气体的体积不小于多少?
23.将油箱注满k升油后,轿车可行驶的总路程s(单位:千米)与平均耗油量a(单位:升/千米)之间是反比例函数关系s=(k是常数,k≠0).已知某轿车油箱注满油后,当平均耗油量为0.1升/千米时,可行驶700千米.
(1)求该轿车可行驶的总路程s与平均耗油量a之间的函数解析式;
(2)当平均耗油量为0.08升/千米时,该轿车可以行驶多少千米?
24.1896年,挪威生理学家古德贝发现,每个人有一条腿迈出的步子比另一条腿迈出的步子长的特点,这就导致每个人在蒙上眼睛行走时,虽然主观上沿某一方向直线前进,但实际上走出的是一个大圆圈!这就是有趣的“瞎转圈”现象.经研究,某人蒙上眼睛走出的大圆圈的半径y/米是其两腿迈出的步长之差x/厘米(x>0)的反比例函数,其图象如图所示.
请根据图象中的信息解决下列问题:
(1)求y与x之间的函数表达式;
(2)当某人两腿迈出的步长之差为0.5厘米时,他蒙上眼睛走出的大圆圈的半径为 米;
(3)若某人蒙上眼睛走出的大圆圈的半径不小于35米,则其两腿迈出的步长之差最多是多少厘米?
答案提示
1.A.2.C.3.D.4.D.5.C.6.C.7.C.8.C.9.B.
10.解:①点P是动点,
∴BP与AP不一定相等,
∴△BOP与△AOP不一定全等,故①不正确;
②设P(m,n),
∴BP∥y轴,
∴B(m,),
∴BP=|﹣n|,
∴S△BOP=×|﹣n|×|m|=|3﹣mn|,
∵PA∥x轴,
∴A(,n)
∴AP=|﹣m|,
∴SAOP=×|﹣m|×|n|=|3﹣mn|,
∴S△AOP=S△BOP,②正确;
③如图1,作PE⊥OB于E,PF⊥OA于F,
∵S△AOP=S△BOP,OA=OB,
∴PE=PF,
∵PE=PF,PE⊥OB,PF⊥OA,
∴OP平分∠AOB,③正确;
④如图2,延长BP交x轴于N,延长AP交y轴于M,
∴AM⊥y轴,BN⊥x轴,又∠MON=90°,
∴四边形OMPN是矩形,
∵点A,B在双曲线y=上,
∴S△AMO=S△BNO=3,
∵S△BOP=2,
∴S△PMO=S△PNO=1,
∴S矩形OMPN=2,
∴mn=2,
∴m=,
∴BP=|﹣n|=|3n﹣n|=2|n|,
AP=|﹣m|=||,
∴S△ABP=×2|n|×||=4,④错误;
故选:B.
y=false. 12.y=. 13.6. 14.y=.
15. 16.3800元 17..
18.解:(1)∵每个台阶的高和宽分别是1和2,
∴T1(﹣16,1),T2(﹣14,2),T3(﹣12,3),T4(﹣10,4),T5(﹣8,5),T6(﹣6,6),T7(﹣4,7),T8(﹣2,8),
∵L过点T1,
∴k=﹣16×1=﹣16,
故答案为:﹣16;
(2)∵L过点T4,
∴k=﹣10×4=﹣40,
∴反比例函数解析式为:y=﹣,
当x=﹣8时,y=5,
∴T5在反比例函数图象上,
∴m=5,
故答案为:5;
(3)若曲线L过点T1(﹣16,1),T8(﹣2,8)时,k=﹣16,
若曲线L过点T2(﹣14,2),T7(﹣4,7)时,k=﹣14×2=﹣28,
若曲线L过点T3(﹣12,3),T6(﹣6,6)时,k=﹣12×3=﹣36,
若曲线L过点T4(﹣10,4),T5(﹣8,5)时,k=﹣40,
∵曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,
∴﹣36<k<﹣28,
∴整数k=﹣35,﹣34,﹣33,﹣32,﹣31,﹣30,﹣29共7个,
∴答案为:7.
19.解:(1)∵ vt=480,且全程速度限定为不超过120千米/小时,
∴ v关于t的函数表达式为:v=false(0≤t≤4);
(2)① 8点至12点48分时间长为false小时,8点至14点时间长为6小时,
将t=6代入v=false得v=80;将t=false代入v=false得v=100.
∴ 小汽车行驶速度v的范围为:80≤v≤100.
② 方方不能在当天11点30分前到达B地.理由如下:
8点至11点30分时间长为false小时,将t=false代入v=false得v=false>120千米/小时,超速了.
故方方不能在当天11点30分前到达B地.
20.解:(1)从表格可以看出xy=6,
∴墨水盖住的数据是6÷1.5=4;
故答案为4;
(2)由xy=6,得到y=,y随x的增大而减少;
故答案为y=;减少;
(3)S1=OA?OC=k=6,S2=OD?OF=k=6,
∴S1=S2;
(4)∵S四边形OCBA=OA?OB=6,S△OCG=OD?OG=×2=1,S△OCG=OA?OH=×2=1,
∴S四边形OGBH=S四边形OCBA﹣S△OCG﹣S△OAH=6﹣1﹣1=4;
故答案为4;
21.解:(1)∵一次函数y=x+1与x轴和y轴分别交于点A和点B,
∴∠CAE=45°,即△CAE为等腰直角三角形,
∴AE=CE,
∵AC=,即,
解得:AE=CE=3,
在y=x+1中,令y=0,则x=﹣1,
∴A(﹣1,0),
∴OE=2,CE=3,
∴C(2,3),
∴k=2×3=6,
∴反比例函数表达式为:,
(2)联立:,
解得:x=2或﹣3,
当x=﹣3时,y=﹣2,
∴点D的坐标为(﹣3,﹣2),
∴S△CDE=×3×[2﹣(﹣3)]=.
22.解:(1)设p=,
由题意知120=,
所以k=96,
故p=;
(2)当v=1.6m3时,p==60,
∴气球内气体的气压是60kPa;
(3)当p=150kPa时,v==0.64.
所以为了安全起见,气体的体积应不少于0.64m3.
23.解:(1)把a=0.1,s=700代入s=,得700=
,解得k=70.
∴该轿车可行驶的总路程s与平均耗油量a之间的函数解析式为s=.
(2)把a=0.08代入s=,
得s=875.
答:当平均耗油量为0.08升/千米时,该轿车可以行驶875千米.
24.解:(1)设y与x之间的函数表达式为y=,
∴7=,
∴k=14,
∴y与x之间的函数表达式为y=;
(2)当x=0.5时,y==28米,
∴当某人两腿迈出的步长之差为0.5厘米时,他蒙上眼睛走出的大圆圈的半径为28米;
(3)当y≥35时,即≥35,
∴x≤0.4,
∴某人蒙上眼睛走出的大圆圈的半径不小于35米,则其两腿迈出的步长之差最多是0.4厘米,
故答案为:28.
6.3反比例函数的应用 同步测试
一.选择题
1.一司机驾驶汽车从甲地去乙地,他以80千米/时的平均速度用了6小时到达目的地,当他按原路匀速返回时,汽车的速度v(千米/时)与时间t(小时)的函数关系为( )
A.v= B.v+t=480 C.v= D.v=
2.如图,⊙O的半径为2,双曲线的解析式分别为false和false,则阴影部分的面积为( )
A. false B. false C. false D. false
3.今年,某公司推出一款新手机深受消费者推崇,但价格不菲.为此,某电子商城推出分期付款购买手机的活动,一部售价为9688元的新手机,前期付款3000元,后期每个月分别付相同的数额,则每个月付款额y(元)与付款月数x(x为正整数)之间的函数关系式是( )
A. B. C. D.
4.(2020?宁夏)如图,函数y1=x+1与函数y2=的图象相交于点M(1,m),N(﹣2,n).若y1>y2,则x的取值范围是( )
A.x<﹣2或0<x<1 B.x<﹣2或x>1
C.﹣2<x<0或0<x<1 D.﹣2<x<0或x>1
5.今年,某公司推出一款的新手机深受消费者推崇,但价格不菲.为此,某电子商城推出分期付款购买新手机的活动,一部售价为9688元的新手机,前期付款2000元,后期每个月分别付相同的数额,则每个月的付款额y(元)与付款月数x(x为正整数)之间的函数关系式是( )
A.y=+2000 B.y=﹣2000 C.y= D.y=
6.(2020?威海)如图,点P(m,1),点Q(﹣2,n)都在反比例函数y=的图象上.过点P分别向x轴、y轴作垂线,垂足分别为点M,N.连接OP,OQ,PQ.若四边形OMPN的面积记作S1,△POQ的面积记作S2,则( )
A.S1:S2=2:3 B.S1:S2=1:1 C.S1:S2=4:3 D.S1:S2=5:3
7.为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2019年1月开始限产进行治污改造,其月利润y(万元)与月份x之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分,下列选项错误的是( )
A.4月份的利润为50万元
B.治污改造完成后每月利润比前一个月增加30万元
C.治污改造完成前后共有4个月的利润低于100万元
D.9月份该厂利润达到200万元
8.某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强p(Pa)是气球体积V(m3)的反比例函数,且当V=1.5m3时,p=16000Pa,当气球内的气压大于40000Pa时,气球将爆炸,为确保气球不爆炸,气球的体积( )
A.不小于0.5m3 B.不大于0.5m3 C.不小于0.6m3 D.不大于0.6m3
9.如图,在直角坐标系中,Rt△OAB的边OB在y轴上,∠ABO=90°,AB=3,点C在AB上,BC=AB,且∠BOC=∠A,若双曲线y=经过点C,则k的值( )
A. B. C.1 D.2
10.如图,A、B是函数y=(x>0)上两点,点P在第一象限,且在函数y=(x>0)下方,作PB⊥x轴,PA⊥y轴,下列说法正确的是( )
①△AOP≌△BOP; ②S△AOP=S△BOP;
③若OA=OB,则OP平分∠AOB; ④若S△BOP=2,则S△ABP=6.
A.1个 B.2个 C.3个 D.4个
二.填空题
11.若一个三角形的面积是8false 则其底边长y(cm) 与这边上的高x(cm)之间的关系是__________.
12.如图所示,小华设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,在中点O右侧用一个弹簧秤向下拉,改变弹簧秤与点O的距离x(cm),观察弹簧秤的示数y(N)的变化情况.实验数据记录如下:
x(cm)…10
15
20
25 30…
y(N)…30
20
15
12 10…
猜测y与x之间的函数关系,并求出函数关系式为 .
13.反比例函数false的图象上有一点P(2,n),将点P向右平移1个单位,再向下平移1个单位得到点Q.若点Q也在该函数的图象上,则k= .
14.有x个小朋友平均分20个苹果,每人分得的苹果y(每人每个)与x(个)之间的函数关系式为 .
15.老王要把一篇24000字的社会调查报告录入电脑,则其录入的时间t(分)与录入文字的平均速度v(字/分)之间的函数表达式应为t= (v>0).
16.李老师参加了某电脑公司推出的分期付款(无利息)购买电脑活动,他购买的电脑价格为9800元,交了首付之后每月付款y元,x个月结清余款,y与x满足如图的函数解析式,通过以上信息可知李老师的首付款为________.
17.如图,点P(a,a)是反比例函数在第一象限内的图象上的一个点,以点P为顶点作等边△PAB,使A、B落在x轴上(点A在点B左侧),则△POA的面积是 .
18.如图是8个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作Tm(m为1~8的整数).函数y=(x<0)的图象为曲线L.
(1)若L过点T1,则k= ;
(2)若L过点T4,则它必定还过另一点Tm,则m= ;
(3)若曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,则k的整数值有 个.
三.解答题
19.方方驾驶小汽车匀速地从A地行驶到B地,行驶里程为480千米,设小汽车的行驶时间为t(单位:小时),行驶速股为v(单位:千米/小时),且全程速度限定为不超过120千米/小时.
求v关于t的函数表达式.
(2)方方上午8点驾驶小汽车从A地出发.
①方方需在当天12点48分至14点(含12点48分和14点)间到达B地.求小汽车行驶速度v的范围.
②方方能否在当天11点30分前到达B地?说明理由.
20.小亮在研究矩形的面积S与矩形的边长x,y之间的关系时,得到如表数据:
x
0.5
1
1.5
2
3
4
6
12
y
12
6
■
3
2
1.5
1
0.5
结果发现一个数据被墨水涂黑了,
(1)被墨水涂黑的数据为 ;
(2)y与x的函数关系式为 ,且y随x的增大而 ;
(3)如图是小亮画出的y关于x的函数图象,点B、E均在该函数的图象上,其中矩形OABC的面积记为S1,矩形ODEF的面积记为S2,请判断S1与S2的大小关系,并说明理由;
(4)在(3)的条件下,DE交BC于点G,反比例函数y=的图象经过点G交AB于点H,连接OG、OH,则四边形OGBH的面积为 .
21.(2020?鞍山)如图,在平面直角坐标系中,一次函数y=x+1的图象与x轴,y轴的交点分别为点A,点B,与反比例函数y=(k≠0)的图象交于C,D两点,CE⊥x轴于点E,连接DE,AC=3.
(1)求反比例函数的解析式;
(2)求△CDE的面积.
22.某气球内充满了一定量的气体,当温度不变时,气球内气体的压强P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
(1)求这个反比例函数的表达式;
(2)当气球内的体积为气体1.6m3时,求气体压强P的值;
(3)当气球内的气体压强大于150kPa时,气球将爆炸,为了安全起见,气体的体积不小于多少?
23.将油箱注满k升油后,轿车可行驶的总路程s(单位:千米)与平均耗油量a(单位:升/千米)之间是反比例函数关系s=(k是常数,k≠0).已知某轿车油箱注满油后,当平均耗油量为0.1升/千米时,可行驶700千米.
(1)求该轿车可行驶的总路程s与平均耗油量a之间的函数解析式;
(2)当平均耗油量为0.08升/千米时,该轿车可以行驶多少千米?
24.1896年,挪威生理学家古德贝发现,每个人有一条腿迈出的步子比另一条腿迈出的步子长的特点,这就导致每个人在蒙上眼睛行走时,虽然主观上沿某一方向直线前进,但实际上走出的是一个大圆圈!这就是有趣的“瞎转圈”现象.经研究,某人蒙上眼睛走出的大圆圈的半径y/米是其两腿迈出的步长之差x/厘米(x>0)的反比例函数,其图象如图所示.
请根据图象中的信息解决下列问题:
(1)求y与x之间的函数表达式;
(2)当某人两腿迈出的步长之差为0.5厘米时,他蒙上眼睛走出的大圆圈的半径为 米;
(3)若某人蒙上眼睛走出的大圆圈的半径不小于35米,则其两腿迈出的步长之差最多是多少厘米?
答案提示
1.A.2.C.3.D.4.D.5.C.6.C.7.C.8.C.9.B.
10.解:①点P是动点,
∴BP与AP不一定相等,
∴△BOP与△AOP不一定全等,故①不正确;
②设P(m,n),
∴BP∥y轴,
∴B(m,),
∴BP=|﹣n|,
∴S△BOP=×|﹣n|×|m|=|3﹣mn|,
∵PA∥x轴,
∴A(,n)
∴AP=|﹣m|,
∴SAOP=×|﹣m|×|n|=|3﹣mn|,
∴S△AOP=S△BOP,②正确;
③如图1,作PE⊥OB于E,PF⊥OA于F,
∵S△AOP=S△BOP,OA=OB,
∴PE=PF,
∵PE=PF,PE⊥OB,PF⊥OA,
∴OP平分∠AOB,③正确;
④如图2,延长BP交x轴于N,延长AP交y轴于M,
∴AM⊥y轴,BN⊥x轴,又∠MON=90°,
∴四边形OMPN是矩形,
∵点A,B在双曲线y=上,
∴S△AMO=S△BNO=3,
∵S△BOP=2,
∴S△PMO=S△PNO=1,
∴S矩形OMPN=2,
∴mn=2,
∴m=,
∴BP=|﹣n|=|3n﹣n|=2|n|,
AP=|﹣m|=||,
∴S△ABP=×2|n|×||=4,④错误;
故选:B.
y=false. 12.y=. 13.6. 14.y=.
15. 16.3800元 17..
18.解:(1)∵每个台阶的高和宽分别是1和2,
∴T1(﹣16,1),T2(﹣14,2),T3(﹣12,3),T4(﹣10,4),T5(﹣8,5),T6(﹣6,6),T7(﹣4,7),T8(﹣2,8),
∵L过点T1,
∴k=﹣16×1=﹣16,
故答案为:﹣16;
(2)∵L过点T4,
∴k=﹣10×4=﹣40,
∴反比例函数解析式为:y=﹣,
当x=﹣8时,y=5,
∴T5在反比例函数图象上,
∴m=5,
故答案为:5;
(3)若曲线L过点T1(﹣16,1),T8(﹣2,8)时,k=﹣16,
若曲线L过点T2(﹣14,2),T7(﹣4,7)时,k=﹣14×2=﹣28,
若曲线L过点T3(﹣12,3),T6(﹣6,6)时,k=﹣12×3=﹣36,
若曲线L过点T4(﹣10,4),T5(﹣8,5)时,k=﹣40,
∵曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,
∴﹣36<k<﹣28,
∴整数k=﹣35,﹣34,﹣33,﹣32,﹣31,﹣30,﹣29共7个,
∴答案为:7.
19.解:(1)∵ vt=480,且全程速度限定为不超过120千米/小时,
∴ v关于t的函数表达式为:v=false(0≤t≤4);
(2)① 8点至12点48分时间长为false小时,8点至14点时间长为6小时,
将t=6代入v=false得v=80;将t=false代入v=false得v=100.
∴ 小汽车行驶速度v的范围为:80≤v≤100.
② 方方不能在当天11点30分前到达B地.理由如下:
8点至11点30分时间长为false小时,将t=false代入v=false得v=false>120千米/小时,超速了.
故方方不能在当天11点30分前到达B地.
20.解:(1)从表格可以看出xy=6,
∴墨水盖住的数据是6÷1.5=4;
故答案为4;
(2)由xy=6,得到y=,y随x的增大而减少;
故答案为y=;减少;
(3)S1=OA?OC=k=6,S2=OD?OF=k=6,
∴S1=S2;
(4)∵S四边形OCBA=OA?OB=6,S△OCG=OD?OG=×2=1,S△OCG=OA?OH=×2=1,
∴S四边形OGBH=S四边形OCBA﹣S△OCG﹣S△OAH=6﹣1﹣1=4;
故答案为4;
21.解:(1)∵一次函数y=x+1与x轴和y轴分别交于点A和点B,
∴∠CAE=45°,即△CAE为等腰直角三角形,
∴AE=CE,
∵AC=,即,
解得:AE=CE=3,
在y=x+1中,令y=0,则x=﹣1,
∴A(﹣1,0),
∴OE=2,CE=3,
∴C(2,3),
∴k=2×3=6,
∴反比例函数表达式为:,
(2)联立:,
解得:x=2或﹣3,
当x=﹣3时,y=﹣2,
∴点D的坐标为(﹣3,﹣2),
∴S△CDE=×3×[2﹣(﹣3)]=.
22.解:(1)设p=,
由题意知120=,
所以k=96,
故p=;
(2)当v=1.6m3时,p==60,
∴气球内气体的气压是60kPa;
(3)当p=150kPa时,v==0.64.
所以为了安全起见,气体的体积应不少于0.64m3.
23.解:(1)把a=0.1,s=700代入s=,得700=
,解得k=70.
∴该轿车可行驶的总路程s与平均耗油量a之间的函数解析式为s=.
(2)把a=0.08代入s=,
得s=875.
答:当平均耗油量为0.08升/千米时,该轿车可以行驶875千米.
24.解:(1)设y与x之间的函数表达式为y=,
∴7=,
∴k=14,
∴y与x之间的函数表达式为y=;
(2)当x=0.5时,y==28米,
∴当某人两腿迈出的步长之差为0.5厘米时,他蒙上眼睛走出的大圆圈的半径为28米;
(3)当y≥35时,即≥35,
∴x≤0.4,
∴某人蒙上眼睛走出的大圆圈的半径不小于35米,则其两腿迈出的步长之差最多是0.4厘米,
故答案为:28.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
