8.1中学生的视力情况调查(2)-苏科版九年级数学下册巩固训练(含答案)
文档属性
| 名称 | 8.1中学生的视力情况调查(2)-苏科版九年级数学下册巩固训练(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 484.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 18:49:38 | ||
图片预览




文档简介
8.1中学生的视力情况调查(2)-苏科版九年级数学下册 巩固训练
一、选择题
1、今年3月,某校举行“好声音”校园歌曲大赛,有9名同学参加选拔赛,所得分数互不相同,按成绩取前4名进入决赛,若已知某同学分数,要判断他能否进入决赛,只需知道9名同学分数的( )
A.中位数 B.众数 C.平均数 D.方差
2、甲、乙两个合唱队队员的平均身高为170 cm,方差分别是、,>,则两个队的队员的身高较整齐的是( )
A.甲队 B.乙队 C.两队一样整齐 D.不能确定
3、下列说法正确的是( )
A.若一个游戏的中奖率是,则连续做10次这样的游戏一定会有一次中奖
B.为了解全国中学生的心理健康情况,应该采用普查的方式
C.一组数据6,8,7,8,8,9,10的众数和中位数都是8
D.若甲、乙组两组数据的方差分别是s甲2=0.01,s乙2=0.1,则乙组数据更稳定
4、抽样调查是只抽取一部分对象进行调查,然后根据调查数据推断全体对象的情况的一种方法.数学活动课上,兴趣小组用抽样调查的方法估计“瓶子中有多少粒豆子?”,具体操作如下:第一步,从瓶子中取出一些豆子,记录这些豆子的粒数为80粒;第二步,给这80粒豆子做上记号;第三步,把这些豆子放回瓶子里,充分摇匀;第四步,从瓶子中再取出一些豆子,记录这些豆子的粒数为100粒,其中带有记号的豆子的粒数为20粒,请你估计瓶子中有多少粒豆子( )
A.100粒 B.180粒 C.200粒 D.400粒
5、某研究机构经过抽样调查,发现当地老年人的养老模式主要有A,B,C,D,E五种,抽样调查的统计结果如图,那么下列说法不正确的是( )
A.选择A型养老的频率是 B.选择养老模式E的人数最多
C.估计当地30000个老年人中有8000人选择C型养老 D.样本容量是1500
6、下列说法正确的是( )
A.若一个游戏的中奖率是,则连续做10次这样的游戏一定会有一次中奖
B.为了解全国中学生的心理健康情况,应该采用普查的方式
C.一组数据6,8,7,8,8,9,10的众数和中位数都是8
D.若甲、乙组两组数据的方差分别是s甲2=0.01,s乙2=0.1,则乙组数据更稳定
7、某中学生环保小组抽样调查了某社区10户家庭1周内使用环保方便袋的数量,结果为(单位:只):6、5、7、8、7、5、8、10、5、9.利用这些数据估计该社区2000户家庭1周内使用环保方便袋约( )
A.21000只 B.20000只 C.14000只 D.98000只
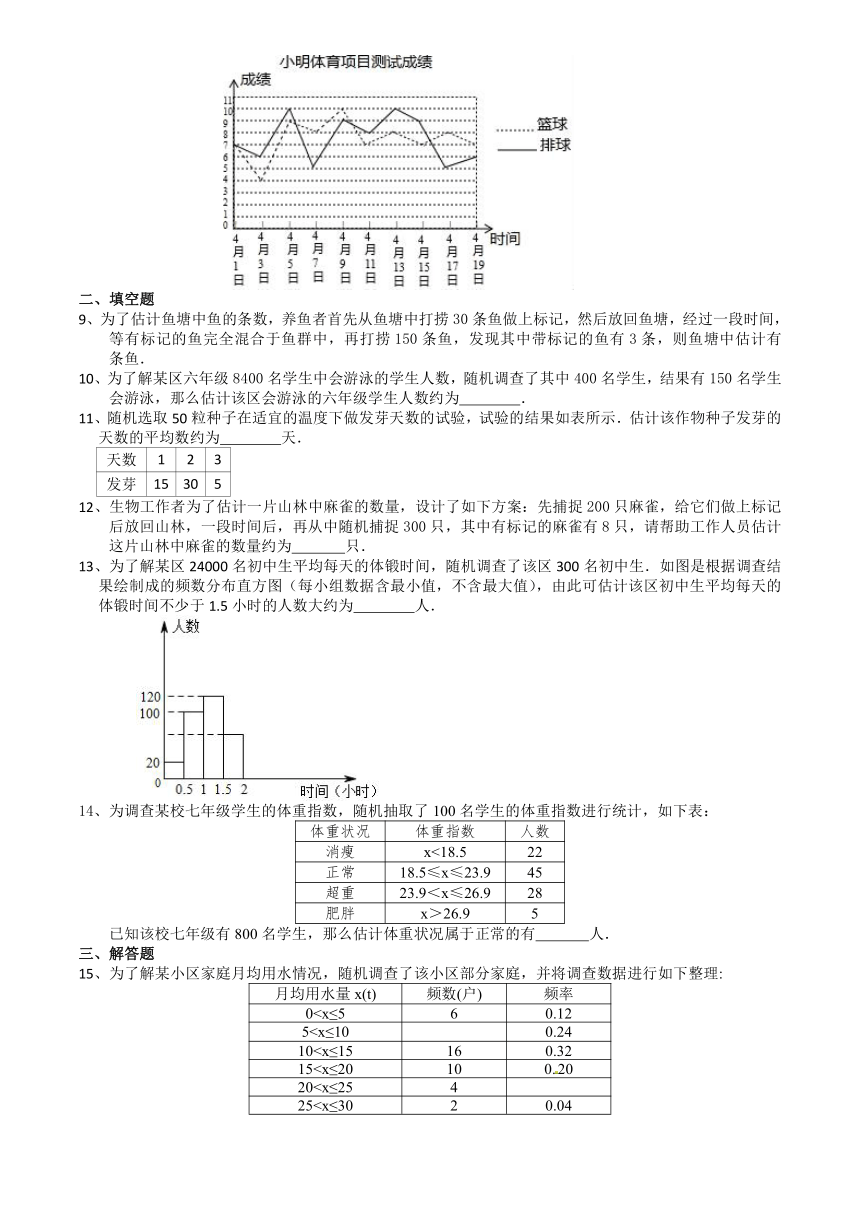
8、在体育中考项目中考生可在篮球、排球中选考一项.小明为了选择一项参加体育中考,将自己的10次测验成绩进行比较并制作了折线统计图,依据图中信息小明选择哪一项参加体育中考更合适,并说明理由, .
二、填空题
9、为了估计鱼塘中鱼的条数,养鱼者首先从鱼塘中打捞30条鱼做上标记,然后放回鱼塘,经过一段时间,等有标记的鱼完全混合于鱼群中,再打捞150条鱼,发现其中带标记的鱼有3条,则鱼塘中估计有 条鱼.
10、为了解某区六年级8400名学生中会游泳的学生人数,随机调查了其中400名学生,结果有150名学生会游泳,那么估计该区会游泳的六年级学生人数约为 .
11、随机选取50粒种子在适宜的温度下做发芽天数的试验,试验的结果如表所示.估计该作物种子发芽的天数的平均数约为 天.
天数 1 2 3
发芽 15 30 5
12、生物工作者为了估计一片山林中麻雀的数量,设计了如下方案:先捕捉200只麻雀,给它们做上标记后放回山林,一段时间后,再从中随机捕捉300只,其中有标记的麻雀有8只,请帮助工作人员估计这片山林中麻雀的数量约为 只.
13、为了解某区24000名初中生平均每天的体锻时间,随机调查了该区300名初中生.如图是根据调查结果绘制成的频数分布直方图(每小组数据含最小值,不含最大值),由此可估计该区初中生平均每天的体锻时间不少于1.5小时的人数大约为 人.
14、为调查某校七年级学生的体重指数,随机抽取了100名学生的体重指数进行统计,如下表:
体重状况 体重指数 人数
消瘦 x<18.5 22
正常 18.5≤x≤23.9 45
超重 23.9<x≤26.9 28
肥胖 x>26.9 5
已知该校七年级有800名学生,那么估计体重状况属于正常的有 人.
三、解答题
15、为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理:
月均用水量x(t) 频数(户) 频率
05 0.24
10152025请解答以下问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)求该小区用水量不超过15 t的家庭占被调查家庭总数的百分比;
(3)若该小区有1 000户家庭,根据调查数据估计,该小区月均用水量超过20 t的家庭大约有多少户?
16、为了打造书香城市,截止2019年3月洛阳市有17家河洛书苑书房对社会免费开放.某书房为了解读者阅读的情况,随机调查了部分读者在一周内借阅图书的次数,并制成如图不完整的统计图表.
读者借阅图书的次数统计表
借阅图书的次数 1次 2次 3次 4次 5次及以上
人数 7 13 a 10 3
请你根据统计图表中的信息,解答下列问题:
(1)a= ,b= ;
(2)这组数据的众数为 ,中位数为 ;
(3)请计算扇形统计图中的“4次”所对应的圆心角的度数;
(4)据统计该书房一周共有2000位不同的读者,根据以上调查结果,请你计算出一周内借阅图书“4次及以上”的读者人数.
17、甲、乙两种水稻试验品种连续5年的平均单位面积产量(单位:t/hm2)如表,试根据这组数据估计
哪一种水稻品种好.
品种 第1年 第2年 第3年 第4年 第5年
甲 9.8 9.9 10.1 10 10.2
乙 9.4 10.3 10.8 9.7 9.8
18、某校组织学生参加“新冠肺炎”防疫知识竞赛,从中抽取了部分学生成绩进行统计,并按照成绩从低到高分成A,B,C,D,E五个小组,绘制统计图如表(未完成),解答下列问题:
(1)样本容量为 ,频数分布直方图中a= ;
(2)扇形统计图中E小组所对应的扇形圆心角为n°,求n的值并补全频数分布直方图;
(3)若成绩在80分以上(不含80分)为优秀,全校共有3000名学生,估计成绩优秀的学生有多少名?
19、某校计划成立下列学生社团:A.合唱团;B.英语俱乐部;C.动漫创作社;D.文学社;E.航模工作室.为了解同学们对上述学生社团的喜爱情况,某课题小组在全校学生中随机抽取了部分同学,进行“你最喜爱的一个学生社团”的调査,根据调查结果绘制了如下尚不完整的统计图.
请根据以上信息,解决下列问题:
(1)本次接受调查的学生共有 人.
(2)补全条形统计图,扇形统计图中D选项所对应扇形的圆心角为 °;
(3)若该学校共有学生300,估计该学校学生中喜爱合唱团和动漫创作社的总人数.
20、某校开展爱“我容城,创卫同行”的活动,倡议学生利用双休日在浜江公园参加评选活动,为了了解同学们劳动时间,学校随机调查了部分同学劳动的时间,并用得到的数据绘制了不完整的统计图,根据图中信息解答下列问题:
(1)将条形统计图补充完整;
(2)抽查的学生劳动时间的众数为 中位数为 .
(3)已知全校学生人数为1200人,请估算该校学生参加义务劳动2小时的有多少人?
8.1中学生的视力情况调查(2)-苏科版九年级数学下册 巩固训练(答案)
一、选择题
1、今年3月,某校举行“好声音”校园歌曲大赛,有9名同学参加选拔赛,所得分数互不相同,按成绩取前4名进入决赛,若已知某同学分数,要判断他能否进入决赛,只需知道9名同学分数的( A )
A.中位数 B.众数 C.平均数 D.方差
2、甲、乙两个合唱队队员的平均身高为170 cm,方差分别是、,>,则两个队的队员的身高较整齐的是(B )
A.甲队 B.乙队 C.两队一样整齐 D.不能确定
3、下列说法正确的是( )
A.若一个游戏的中奖率是,则连续做10次这样的游戏一定会有一次中奖
B.为了解全国中学生的心理健康情况,应该采用普查的方式
C.一组数据6,8,7,8,8,9,10的众数和中位数都是8
D.若甲、乙组两组数据的方差分别是s甲2=0.01,s乙2=0.1,则乙组数据更稳定
【解答】解:A、若一个游戏的中奖率是,则连续做10次这样的游戏可能中奖,也可能不中奖,故A不符合题意;
B、为了解全国中学生的心理健康情况,应该采用抽样调查的方式,故B不符合题意;
C、一组数据6,8,7,8,8,9,10的众数和中位数都是8,故C符合题意;
D、若甲、乙组两组数据的方差分别是s甲2=0.01,s乙2=0.1,则甲组数据更稳定,故D不符合题意;
故选:C.
4、抽样调查是只抽取一部分对象进行调查,然后根据调查数据推断全体对象的情况的一种方法.数学活动课上,兴趣小组用抽样调查的方法估计“瓶子中有多少粒豆子?”,具体操作如下:第一步,从瓶子中取出一些豆子,记录这些豆子的粒数为80粒;第二步,给这80粒豆子做上记号;第三步,把这些豆子放回瓶子里,充分摇匀;第四步,从瓶子中再取出一些豆子,记录这些豆子的粒数为100粒,其中带有记号的豆子的粒数为20粒,请你估计瓶子中有多少粒豆子( )
A.100粒 B.180粒 C.200粒 D.400粒
【解析】设瓶子中有x粒豆子,根据题意得:,解得:x=400,
经检验x=400是原方程的解,
答:估计瓶子中豆子的数量约为400粒.
故选D.
5、某研究机构经过抽样调查,发现当地老年人的养老模式主要有A,B,C,D,E五种,抽样调查的统计结果如图,那么下列说法不正确的是( )
A.选择A型养老的频率是 B.选择养老模式E的人数最多
C.估计当地30000个老年人中有8000人选择C型养老 D.样本容量是1500
【解析】A、选择A型养老的频率是,此选项说法正确;
B、选择养老模式E的人数最多,此选项说法正确;
C.可以估计当地30000个老年人中选择C型养老的人数为300004000人,此选项说法错误;
D、样本容量是1500,此选项说法正确;
故选C.
6、下列说法正确的是( )
A.若一个游戏的中奖率是,则连续做10次这样的游戏一定会有一次中奖
B.为了解全国中学生的心理健康情况,应该采用普查的方式
C.一组数据6,8,7,8,8,9,10的众数和中位数都是8
D.若甲、乙组两组数据的方差分别是s甲2=0.01,s乙2=0.1,则乙组数据更稳定
【解答】解:A、若一个游戏的中奖率是,则连续做10次这样的游戏可能中奖,也可能不中奖,故A不符合题意;
B、为了解全国中学生的心理健康情况,应该采用抽样调查的方式,故B不符合题意;
C、一组数据6,8,7,8,8,9,10的众数和中位数都是8,故C符合题意;
D、若甲、乙组两组数据的方差分别是s甲2=0.01,s乙2=0.1,则甲组数据更稳定,故D不符合题意;
故选:C.
7、某中学生环保小组抽样调查了某社区10户家庭1周内使用环保方便袋的数量,结果为(单位:只):6、5、7、8、7、5、8、10、5、9.利用这些数据估计该社区2000户家庭1周内使用环保方便袋约( )
A.21000只 B.20000只 C.14000只 D.98000只
【解析】每户平均每周使用方便袋的数量为:(6+5+7+8+7+5+8+10+5+9)=7(只),
故该社区2000户家庭1周内使用环保方便袋约为:2000×7=14000(只).
故选:C.
8、在体育中考项目中考生可在篮球、排球中选考一项.小明为了选择一项参加体育中考,将自己的10次测验成绩进行比较并制作了折线统计图,依据图中信息小明选择哪一项参加体育中考更合适,并说明理由, .
【解答】解:由折线统计图知,篮球的成绩为:7、4、9、8、10、7、8、7、8、7,
排球的成绩为:7、6、10、5、9、8、10、9、5、6,
∵=×(7+4+9+8+10+7+8+7+8+7)=7.5,
=×(7+6+10+5+9+8+10+9+5+6)=7.5,
∴=×[(7﹣7.5)2+(4﹣7.5)2+(9﹣7.5)2+(8﹣7.5)2+(10﹣7.5)2+(7﹣7.5)2+(8﹣7.5)2+(7﹣7.5)2+(8﹣7.5)2+(7﹣7.5)2]=2.25,
=×[(7﹣7.5)2+(6﹣7.5)2+(10﹣7.5)2+(5﹣7.5)2+(9﹣7.5)2+(8﹣7.5)2+(10﹣7.5)2+(9﹣7.5)2+(5﹣7.5)2+(6﹣7.5)2]=3.45,
由于=,但<,
则篮球和排球的平均得分相同,但篮球发挥更稳定,
所以选择篮球参加中考,
故答案为:篮球,理由:篮球和排球的平均得分相同,但篮球发挥更稳定.
二、填空题
9、为了估计鱼塘中鱼的条数,养鱼者首先从鱼塘中打捞30条鱼做上标记,然后放回鱼塘,经过一段时间,等有标记的鱼完全混合于鱼群中,再打捞150条鱼,发现其中带标记的鱼有3条,则鱼塘中估计有 条鱼.
【解析】根据题意得:301500(条),
答:鱼塘中估计有1500条鱼.
故答案为1500.
10、为了解某区六年级8400名学生中会游泳的学生人数,随机调查了其中400名学生,结果有150名学生会游泳,那么估计该区会游泳的六年级学生人数约为 .
【解析】84003150.
答:估计该区会游泳的六年级学生人数约为3150.
故答案为3150.
11、随机选取50粒种子在适宜的温度下做发芽天数的试验,试验的结果如表所示.估计该作物种子发芽的天数的平均数约为 天.
天数 1 2 3
发芽 15 30 5
【解答】解:估计该作物种子发芽的天数的平均数约为=1.8(天),
故答案为:1.8.
12、生物工作者为了估计一片山林中麻雀的数量,设计了如下方案:先捕捉200只麻雀,给它们做上标记后放回山林,一段时间后,再从中随机捕捉300只,其中有标记的麻雀有8只,请帮助工作人员估计这片山林中麻雀的数量约为 只.
【解析】2007500(只),
即这片山林中麻雀的数量约为7500只,
故答案为7500.
13、为了解某区24000名初中生平均每天的体锻时间,随机调查了该区300名初中生.如图是根据调查结果绘制成的频数分布直方图(每小组数据含最小值,不含最大值),由此可估计该区初中生平均每天的体锻时间不少于1.5小时的人数大约为 人.
【解答】解:估计该区初中生平均每天的体锻时间不少于1.5小时的人数大约为24000×=4800(人),
故答案为:4800.
14、为调查某校七年级学生的体重指数,随机抽取了100名学生的体重指数进行统计,如下表:
体重状况 体重指数 人数
消瘦 x<18.5 22
正常 18.5≤x≤23.9 45
超重 23.9<x≤26.9 28
肥胖 x>26.9 5
已知该校七年级有800名学生,那么估计体重状况属于正常的有360 人.
三、解答题
15、为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理:
月均用水量x(t) 频数(户) 频率
05 0.24
10152025请解答以下问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)求该小区用水量不超过15 t的家庭占被调查家庭总数的百分比;
(3)若该小区有1 000户家庭,根据调查数据估计,该小区月均用水量超过20 t的家庭大约有多少户?
解:(1)根据频数分布表可知0<x≤5频数为6,频率为0.12,则
6÷0.12=50,50×0.24=12(户),
4÷50=0.08,
故表格从上往下依次是:12户和0.08;
频数分布直方图补充如下:
(2)用水量不超过15吨是前三组,(0.12+0.24+0.32)×100%=68%;
(3)1000×(0.04+0.08)=120(户).
16、为了打造书香城市,截止2019年3月洛阳市有17家河洛书苑书房对社会免费开放.某书房为了解读者阅读的情况,随机调查了部分读者在一周内借阅图书的次数,并制成如图不完整的统计图表.
读者借阅图书的次数统计表
借阅图书的次数 1次 2次 3次 4次 5次及以上
人数 7 13 a 10 3
请你根据统计图表中的信息,解答下列问题:
(1)a= ,b= ;
(2)这组数据的众数为 ,中位数为 ;
(3)请计算扇形统计图中的“4次”所对应的圆心角的度数;
(4)据统计该书房一周共有2000位不同的读者,根据以上调查结果,请你计算出一周内借阅图书“4次及以上”的读者人数.
答案:(1)a=17,b=20;(2)众数为3,中位数为3;(3)72°;(4)520人.
17、甲、乙两种水稻试验品种连续5年的平均单位面积产量(单位:t/hm2)如表,试根据这组数据估计
哪一种水稻品种好.
品种 第1年 第2年 第3年 第4年 第5年
甲 9.8 9.9 10.1 10 10.2
乙 9.4 10.3 10.8 9.7 9.8
【解析】根据表格中的数据求得甲的平均数=(9.8+9.9+10.1+10+10.2)÷5=10;
乙的平均数=(9.4+10.3+10.8+9.7+9.8)÷5=10,
甲种水稻产量的方差是:
[(9.8﹣10)2+(9.9﹣10)2+(10.1﹣10)2+(10﹣10)2+(10.2﹣10)2]=0.02,
乙种水稻产量的方差是:
[(9.4﹣10)2+(10.3﹣10)2+(10.8﹣10)2+(9.7﹣10)2+(9.8﹣10)2]=0.244.
∵0.02<0.244, ∴产量比较稳定的水稻品种是甲.
因为甲、乙两种水稻单位面积产量的平均数相等,甲种方差小于乙种方差,
所以甲种水稻品种好.
18、某校组织学生参加“新冠肺炎”防疫知识竞赛,从中抽取了部分学生成绩进行统计,并按照成绩从低到高分成A,B,C,D,E五个小组,绘制统计图如表(未完成),解答下列问题:
(1)样本容量为 ,频数分布直方图中a= ;
(2)扇形统计图中E小组所对应的扇形圆心角为n°,求n的值并补全频数分布直方图;
(3)若成绩在80分以上(不含80分)为优秀,全校共有3000名学生,估计成绩优秀的学生有多少名?
【解答】解:(1)学生总数是40÷20%=200(人),
则a=200×8%=16;
故答案为:200;16;
(2)n=360°×=43.2°.
C组的人数是:200×25%=50.如图所示:
(3)根据题意得:
3000×=1410(名)
答:成绩优秀的学生有1410名.
19、某校计划成立下列学生社团:A.合唱团;B.英语俱乐部;C.动漫创作社;D.文学社;E.航模工作室.为了解同学们对上述学生社团的喜爱情况,某课题小组在全校学生中随机抽取了部分同学,进行“你最喜爱的一个学生社团”的调査,根据调查结果绘制了如下尚不完整的统计图.
请根据以上信息,解决下列问题:
(1)本次接受调查的学生共有 人.
(2)补全条形统计图,扇形统计图中D选项所对应扇形的圆心角为 °;
(3)若该学校共有学生300,估计该学校学生中喜爱合唱团和动漫创作社的总人数.
【解答】解:(1)本次接受调查的学生共有90÷45%=200(人),
故答案为:200;
(2)D社团人数为200﹣(26+90+34+10)=40(人),
补全图形如下:
扇形统计图中D选项所对应扇形的圆心角为360°×=72°,
故答案为:72;
(3)估计该学校学生中喜爱合唱团和动漫创作社的总人数为300×=90(人).
20、某校开展爱“我容城,创卫同行”的活动,倡议学生利用双休日在浜江公园参加评选活动,为了了解同学们劳动时间,学校随机调查了部分同学劳动的时间,并用得到的数据绘制了不完整的统计图,根据图中信息解答下列问题:
(1)将条形统计图补充完整;
(2)抽查的学生劳动时间的众数为 中位数为 .
(3)已知全校学生人数为1200人,请估算该校学生参加义务劳动2小时的有多少人?
【解答】解:(1)根据题意得:30÷30%=100(人),
∴学生劳动时间为“1.5小时”的人数为100﹣(12+30+18)=40(人),
补全统计图,如图所示:
(2)根据题意得:抽查的学生劳动时间的众数为1.5小时、中位数为1.5小时,
故答案为:1.5,1.5;
(3)1200×=216,
答:估算该校学生参加义务劳动2小时的有216人.
一、选择题
1、今年3月,某校举行“好声音”校园歌曲大赛,有9名同学参加选拔赛,所得分数互不相同,按成绩取前4名进入决赛,若已知某同学分数,要判断他能否进入决赛,只需知道9名同学分数的( )
A.中位数 B.众数 C.平均数 D.方差
2、甲、乙两个合唱队队员的平均身高为170 cm,方差分别是、,>,则两个队的队员的身高较整齐的是( )
A.甲队 B.乙队 C.两队一样整齐 D.不能确定
3、下列说法正确的是( )
A.若一个游戏的中奖率是,则连续做10次这样的游戏一定会有一次中奖
B.为了解全国中学生的心理健康情况,应该采用普查的方式
C.一组数据6,8,7,8,8,9,10的众数和中位数都是8
D.若甲、乙组两组数据的方差分别是s甲2=0.01,s乙2=0.1,则乙组数据更稳定
4、抽样调查是只抽取一部分对象进行调查,然后根据调查数据推断全体对象的情况的一种方法.数学活动课上,兴趣小组用抽样调查的方法估计“瓶子中有多少粒豆子?”,具体操作如下:第一步,从瓶子中取出一些豆子,记录这些豆子的粒数为80粒;第二步,给这80粒豆子做上记号;第三步,把这些豆子放回瓶子里,充分摇匀;第四步,从瓶子中再取出一些豆子,记录这些豆子的粒数为100粒,其中带有记号的豆子的粒数为20粒,请你估计瓶子中有多少粒豆子( )
A.100粒 B.180粒 C.200粒 D.400粒
5、某研究机构经过抽样调查,发现当地老年人的养老模式主要有A,B,C,D,E五种,抽样调查的统计结果如图,那么下列说法不正确的是( )
A.选择A型养老的频率是 B.选择养老模式E的人数最多
C.估计当地30000个老年人中有8000人选择C型养老 D.样本容量是1500
6、下列说法正确的是( )
A.若一个游戏的中奖率是,则连续做10次这样的游戏一定会有一次中奖
B.为了解全国中学生的心理健康情况,应该采用普查的方式
C.一组数据6,8,7,8,8,9,10的众数和中位数都是8
D.若甲、乙组两组数据的方差分别是s甲2=0.01,s乙2=0.1,则乙组数据更稳定
7、某中学生环保小组抽样调查了某社区10户家庭1周内使用环保方便袋的数量,结果为(单位:只):6、5、7、8、7、5、8、10、5、9.利用这些数据估计该社区2000户家庭1周内使用环保方便袋约( )
A.21000只 B.20000只 C.14000只 D.98000只
8、在体育中考项目中考生可在篮球、排球中选考一项.小明为了选择一项参加体育中考,将自己的10次测验成绩进行比较并制作了折线统计图,依据图中信息小明选择哪一项参加体育中考更合适,并说明理由, .
二、填空题
9、为了估计鱼塘中鱼的条数,养鱼者首先从鱼塘中打捞30条鱼做上标记,然后放回鱼塘,经过一段时间,等有标记的鱼完全混合于鱼群中,再打捞150条鱼,发现其中带标记的鱼有3条,则鱼塘中估计有 条鱼.
10、为了解某区六年级8400名学生中会游泳的学生人数,随机调查了其中400名学生,结果有150名学生会游泳,那么估计该区会游泳的六年级学生人数约为 .
11、随机选取50粒种子在适宜的温度下做发芽天数的试验,试验的结果如表所示.估计该作物种子发芽的天数的平均数约为 天.
天数 1 2 3
发芽 15 30 5
12、生物工作者为了估计一片山林中麻雀的数量,设计了如下方案:先捕捉200只麻雀,给它们做上标记后放回山林,一段时间后,再从中随机捕捉300只,其中有标记的麻雀有8只,请帮助工作人员估计这片山林中麻雀的数量约为 只.
13、为了解某区24000名初中生平均每天的体锻时间,随机调查了该区300名初中生.如图是根据调查结果绘制成的频数分布直方图(每小组数据含最小值,不含最大值),由此可估计该区初中生平均每天的体锻时间不少于1.5小时的人数大约为 人.
14、为调查某校七年级学生的体重指数,随机抽取了100名学生的体重指数进行统计,如下表:
体重状况 体重指数 人数
消瘦 x<18.5 22
正常 18.5≤x≤23.9 45
超重 23.9<x≤26.9 28
肥胖 x>26.9 5
已知该校七年级有800名学生,那么估计体重状况属于正常的有 人.
三、解答题
15、为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理:
月均用水量x(t) 频数(户) 频率
0
10
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)求该小区用水量不超过15 t的家庭占被调查家庭总数的百分比;
(3)若该小区有1 000户家庭,根据调查数据估计,该小区月均用水量超过20 t的家庭大约有多少户?
16、为了打造书香城市,截止2019年3月洛阳市有17家河洛书苑书房对社会免费开放.某书房为了解读者阅读的情况,随机调查了部分读者在一周内借阅图书的次数,并制成如图不完整的统计图表.
读者借阅图书的次数统计表
借阅图书的次数 1次 2次 3次 4次 5次及以上
人数 7 13 a 10 3
请你根据统计图表中的信息,解答下列问题:
(1)a= ,b= ;
(2)这组数据的众数为 ,中位数为 ;
(3)请计算扇形统计图中的“4次”所对应的圆心角的度数;
(4)据统计该书房一周共有2000位不同的读者,根据以上调查结果,请你计算出一周内借阅图书“4次及以上”的读者人数.
17、甲、乙两种水稻试验品种连续5年的平均单位面积产量(单位:t/hm2)如表,试根据这组数据估计
哪一种水稻品种好.
品种 第1年 第2年 第3年 第4年 第5年
甲 9.8 9.9 10.1 10 10.2
乙 9.4 10.3 10.8 9.7 9.8
18、某校组织学生参加“新冠肺炎”防疫知识竞赛,从中抽取了部分学生成绩进行统计,并按照成绩从低到高分成A,B,C,D,E五个小组,绘制统计图如表(未完成),解答下列问题:
(1)样本容量为 ,频数分布直方图中a= ;
(2)扇形统计图中E小组所对应的扇形圆心角为n°,求n的值并补全频数分布直方图;
(3)若成绩在80分以上(不含80分)为优秀,全校共有3000名学生,估计成绩优秀的学生有多少名?
19、某校计划成立下列学生社团:A.合唱团;B.英语俱乐部;C.动漫创作社;D.文学社;E.航模工作室.为了解同学们对上述学生社团的喜爱情况,某课题小组在全校学生中随机抽取了部分同学,进行“你最喜爱的一个学生社团”的调査,根据调查结果绘制了如下尚不完整的统计图.
请根据以上信息,解决下列问题:
(1)本次接受调查的学生共有 人.
(2)补全条形统计图,扇形统计图中D选项所对应扇形的圆心角为 °;
(3)若该学校共有学生300,估计该学校学生中喜爱合唱团和动漫创作社的总人数.
20、某校开展爱“我容城,创卫同行”的活动,倡议学生利用双休日在浜江公园参加评选活动,为了了解同学们劳动时间,学校随机调查了部分同学劳动的时间,并用得到的数据绘制了不完整的统计图,根据图中信息解答下列问题:
(1)将条形统计图补充完整;
(2)抽查的学生劳动时间的众数为 中位数为 .
(3)已知全校学生人数为1200人,请估算该校学生参加义务劳动2小时的有多少人?
8.1中学生的视力情况调查(2)-苏科版九年级数学下册 巩固训练(答案)
一、选择题
1、今年3月,某校举行“好声音”校园歌曲大赛,有9名同学参加选拔赛,所得分数互不相同,按成绩取前4名进入决赛,若已知某同学分数,要判断他能否进入决赛,只需知道9名同学分数的( A )
A.中位数 B.众数 C.平均数 D.方差
2、甲、乙两个合唱队队员的平均身高为170 cm,方差分别是、,>,则两个队的队员的身高较整齐的是(B )
A.甲队 B.乙队 C.两队一样整齐 D.不能确定
3、下列说法正确的是( )
A.若一个游戏的中奖率是,则连续做10次这样的游戏一定会有一次中奖
B.为了解全国中学生的心理健康情况,应该采用普查的方式
C.一组数据6,8,7,8,8,9,10的众数和中位数都是8
D.若甲、乙组两组数据的方差分别是s甲2=0.01,s乙2=0.1,则乙组数据更稳定
【解答】解:A、若一个游戏的中奖率是,则连续做10次这样的游戏可能中奖,也可能不中奖,故A不符合题意;
B、为了解全国中学生的心理健康情况,应该采用抽样调查的方式,故B不符合题意;
C、一组数据6,8,7,8,8,9,10的众数和中位数都是8,故C符合题意;
D、若甲、乙组两组数据的方差分别是s甲2=0.01,s乙2=0.1,则甲组数据更稳定,故D不符合题意;
故选:C.
4、抽样调查是只抽取一部分对象进行调查,然后根据调查数据推断全体对象的情况的一种方法.数学活动课上,兴趣小组用抽样调查的方法估计“瓶子中有多少粒豆子?”,具体操作如下:第一步,从瓶子中取出一些豆子,记录这些豆子的粒数为80粒;第二步,给这80粒豆子做上记号;第三步,把这些豆子放回瓶子里,充分摇匀;第四步,从瓶子中再取出一些豆子,记录这些豆子的粒数为100粒,其中带有记号的豆子的粒数为20粒,请你估计瓶子中有多少粒豆子( )
A.100粒 B.180粒 C.200粒 D.400粒
【解析】设瓶子中有x粒豆子,根据题意得:,解得:x=400,
经检验x=400是原方程的解,
答:估计瓶子中豆子的数量约为400粒.
故选D.
5、某研究机构经过抽样调查,发现当地老年人的养老模式主要有A,B,C,D,E五种,抽样调查的统计结果如图,那么下列说法不正确的是( )
A.选择A型养老的频率是 B.选择养老模式E的人数最多
C.估计当地30000个老年人中有8000人选择C型养老 D.样本容量是1500
【解析】A、选择A型养老的频率是,此选项说法正确;
B、选择养老模式E的人数最多,此选项说法正确;
C.可以估计当地30000个老年人中选择C型养老的人数为300004000人,此选项说法错误;
D、样本容量是1500,此选项说法正确;
故选C.
6、下列说法正确的是( )
A.若一个游戏的中奖率是,则连续做10次这样的游戏一定会有一次中奖
B.为了解全国中学生的心理健康情况,应该采用普查的方式
C.一组数据6,8,7,8,8,9,10的众数和中位数都是8
D.若甲、乙组两组数据的方差分别是s甲2=0.01,s乙2=0.1,则乙组数据更稳定
【解答】解:A、若一个游戏的中奖率是,则连续做10次这样的游戏可能中奖,也可能不中奖,故A不符合题意;
B、为了解全国中学生的心理健康情况,应该采用抽样调查的方式,故B不符合题意;
C、一组数据6,8,7,8,8,9,10的众数和中位数都是8,故C符合题意;
D、若甲、乙组两组数据的方差分别是s甲2=0.01,s乙2=0.1,则甲组数据更稳定,故D不符合题意;
故选:C.
7、某中学生环保小组抽样调查了某社区10户家庭1周内使用环保方便袋的数量,结果为(单位:只):6、5、7、8、7、5、8、10、5、9.利用这些数据估计该社区2000户家庭1周内使用环保方便袋约( )
A.21000只 B.20000只 C.14000只 D.98000只
【解析】每户平均每周使用方便袋的数量为:(6+5+7+8+7+5+8+10+5+9)=7(只),
故该社区2000户家庭1周内使用环保方便袋约为:2000×7=14000(只).
故选:C.
8、在体育中考项目中考生可在篮球、排球中选考一项.小明为了选择一项参加体育中考,将自己的10次测验成绩进行比较并制作了折线统计图,依据图中信息小明选择哪一项参加体育中考更合适,并说明理由, .
【解答】解:由折线统计图知,篮球的成绩为:7、4、9、8、10、7、8、7、8、7,
排球的成绩为:7、6、10、5、9、8、10、9、5、6,
∵=×(7+4+9+8+10+7+8+7+8+7)=7.5,
=×(7+6+10+5+9+8+10+9+5+6)=7.5,
∴=×[(7﹣7.5)2+(4﹣7.5)2+(9﹣7.5)2+(8﹣7.5)2+(10﹣7.5)2+(7﹣7.5)2+(8﹣7.5)2+(7﹣7.5)2+(8﹣7.5)2+(7﹣7.5)2]=2.25,
=×[(7﹣7.5)2+(6﹣7.5)2+(10﹣7.5)2+(5﹣7.5)2+(9﹣7.5)2+(8﹣7.5)2+(10﹣7.5)2+(9﹣7.5)2+(5﹣7.5)2+(6﹣7.5)2]=3.45,
由于=,但<,
则篮球和排球的平均得分相同,但篮球发挥更稳定,
所以选择篮球参加中考,
故答案为:篮球,理由:篮球和排球的平均得分相同,但篮球发挥更稳定.
二、填空题
9、为了估计鱼塘中鱼的条数,养鱼者首先从鱼塘中打捞30条鱼做上标记,然后放回鱼塘,经过一段时间,等有标记的鱼完全混合于鱼群中,再打捞150条鱼,发现其中带标记的鱼有3条,则鱼塘中估计有 条鱼.
【解析】根据题意得:301500(条),
答:鱼塘中估计有1500条鱼.
故答案为1500.
10、为了解某区六年级8400名学生中会游泳的学生人数,随机调查了其中400名学生,结果有150名学生会游泳,那么估计该区会游泳的六年级学生人数约为 .
【解析】84003150.
答:估计该区会游泳的六年级学生人数约为3150.
故答案为3150.
11、随机选取50粒种子在适宜的温度下做发芽天数的试验,试验的结果如表所示.估计该作物种子发芽的天数的平均数约为 天.
天数 1 2 3
发芽 15 30 5
【解答】解:估计该作物种子发芽的天数的平均数约为=1.8(天),
故答案为:1.8.
12、生物工作者为了估计一片山林中麻雀的数量,设计了如下方案:先捕捉200只麻雀,给它们做上标记后放回山林,一段时间后,再从中随机捕捉300只,其中有标记的麻雀有8只,请帮助工作人员估计这片山林中麻雀的数量约为 只.
【解析】2007500(只),
即这片山林中麻雀的数量约为7500只,
故答案为7500.
13、为了解某区24000名初中生平均每天的体锻时间,随机调查了该区300名初中生.如图是根据调查结果绘制成的频数分布直方图(每小组数据含最小值,不含最大值),由此可估计该区初中生平均每天的体锻时间不少于1.5小时的人数大约为 人.
【解答】解:估计该区初中生平均每天的体锻时间不少于1.5小时的人数大约为24000×=4800(人),
故答案为:4800.
14、为调查某校七年级学生的体重指数,随机抽取了100名学生的体重指数进行统计,如下表:
体重状况 体重指数 人数
消瘦 x<18.5 22
正常 18.5≤x≤23.9 45
超重 23.9<x≤26.9 28
肥胖 x>26.9 5
已知该校七年级有800名学生,那么估计体重状况属于正常的有360 人.
三、解答题
15、为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理:
月均用水量x(t) 频数(户) 频率
0
10
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)求该小区用水量不超过15 t的家庭占被调查家庭总数的百分比;
(3)若该小区有1 000户家庭,根据调查数据估计,该小区月均用水量超过20 t的家庭大约有多少户?
解:(1)根据频数分布表可知0<x≤5频数为6,频率为0.12,则
6÷0.12=50,50×0.24=12(户),
4÷50=0.08,
故表格从上往下依次是:12户和0.08;
频数分布直方图补充如下:
(2)用水量不超过15吨是前三组,(0.12+0.24+0.32)×100%=68%;
(3)1000×(0.04+0.08)=120(户).
16、为了打造书香城市,截止2019年3月洛阳市有17家河洛书苑书房对社会免费开放.某书房为了解读者阅读的情况,随机调查了部分读者在一周内借阅图书的次数,并制成如图不完整的统计图表.
读者借阅图书的次数统计表
借阅图书的次数 1次 2次 3次 4次 5次及以上
人数 7 13 a 10 3
请你根据统计图表中的信息,解答下列问题:
(1)a= ,b= ;
(2)这组数据的众数为 ,中位数为 ;
(3)请计算扇形统计图中的“4次”所对应的圆心角的度数;
(4)据统计该书房一周共有2000位不同的读者,根据以上调查结果,请你计算出一周内借阅图书“4次及以上”的读者人数.
答案:(1)a=17,b=20;(2)众数为3,中位数为3;(3)72°;(4)520人.
17、甲、乙两种水稻试验品种连续5年的平均单位面积产量(单位:t/hm2)如表,试根据这组数据估计
哪一种水稻品种好.
品种 第1年 第2年 第3年 第4年 第5年
甲 9.8 9.9 10.1 10 10.2
乙 9.4 10.3 10.8 9.7 9.8
【解析】根据表格中的数据求得甲的平均数=(9.8+9.9+10.1+10+10.2)÷5=10;
乙的平均数=(9.4+10.3+10.8+9.7+9.8)÷5=10,
甲种水稻产量的方差是:
[(9.8﹣10)2+(9.9﹣10)2+(10.1﹣10)2+(10﹣10)2+(10.2﹣10)2]=0.02,
乙种水稻产量的方差是:
[(9.4﹣10)2+(10.3﹣10)2+(10.8﹣10)2+(9.7﹣10)2+(9.8﹣10)2]=0.244.
∵0.02<0.244, ∴产量比较稳定的水稻品种是甲.
因为甲、乙两种水稻单位面积产量的平均数相等,甲种方差小于乙种方差,
所以甲种水稻品种好.
18、某校组织学生参加“新冠肺炎”防疫知识竞赛,从中抽取了部分学生成绩进行统计,并按照成绩从低到高分成A,B,C,D,E五个小组,绘制统计图如表(未完成),解答下列问题:
(1)样本容量为 ,频数分布直方图中a= ;
(2)扇形统计图中E小组所对应的扇形圆心角为n°,求n的值并补全频数分布直方图;
(3)若成绩在80分以上(不含80分)为优秀,全校共有3000名学生,估计成绩优秀的学生有多少名?
【解答】解:(1)学生总数是40÷20%=200(人),
则a=200×8%=16;
故答案为:200;16;
(2)n=360°×=43.2°.
C组的人数是:200×25%=50.如图所示:
(3)根据题意得:
3000×=1410(名)
答:成绩优秀的学生有1410名.
19、某校计划成立下列学生社团:A.合唱团;B.英语俱乐部;C.动漫创作社;D.文学社;E.航模工作室.为了解同学们对上述学生社团的喜爱情况,某课题小组在全校学生中随机抽取了部分同学,进行“你最喜爱的一个学生社团”的调査,根据调查结果绘制了如下尚不完整的统计图.
请根据以上信息,解决下列问题:
(1)本次接受调查的学生共有 人.
(2)补全条形统计图,扇形统计图中D选项所对应扇形的圆心角为 °;
(3)若该学校共有学生300,估计该学校学生中喜爱合唱团和动漫创作社的总人数.
【解答】解:(1)本次接受调查的学生共有90÷45%=200(人),
故答案为:200;
(2)D社团人数为200﹣(26+90+34+10)=40(人),
补全图形如下:
扇形统计图中D选项所对应扇形的圆心角为360°×=72°,
故答案为:72;
(3)估计该学校学生中喜爱合唱团和动漫创作社的总人数为300×=90(人).
20、某校开展爱“我容城,创卫同行”的活动,倡议学生利用双休日在浜江公园参加评选活动,为了了解同学们劳动时间,学校随机调查了部分同学劳动的时间,并用得到的数据绘制了不完整的统计图,根据图中信息解答下列问题:
(1)将条形统计图补充完整;
(2)抽查的学生劳动时间的众数为 中位数为 .
(3)已知全校学生人数为1200人,请估算该校学生参加义务劳动2小时的有多少人?
【解答】解:(1)根据题意得:30÷30%=100(人),
∴学生劳动时间为“1.5小时”的人数为100﹣(12+30+18)=40(人),
补全统计图,如图所示:
(2)根据题意得:抽查的学生劳动时间的众数为1.5小时、中位数为1.5小时,
故答案为:1.5,1.5;
(3)1200×=216,
答:估算该校学生参加义务劳动2小时的有216人.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
