7.6用锐角三角函数解决问题(2)-苏科版九年级数学下册巩固训练(含答案 )
文档属性
| 名称 | 7.6用锐角三角函数解决问题(2)-苏科版九年级数学下册巩固训练(含答案 ) |
|
|
| 格式 | doc | ||
| 文件大小 | 667.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 00:00:00 | ||
图片预览



文档简介
7.6用锐角三角函数解决问题(2)-苏科版九年级数学下册 巩固训练
一、选择题
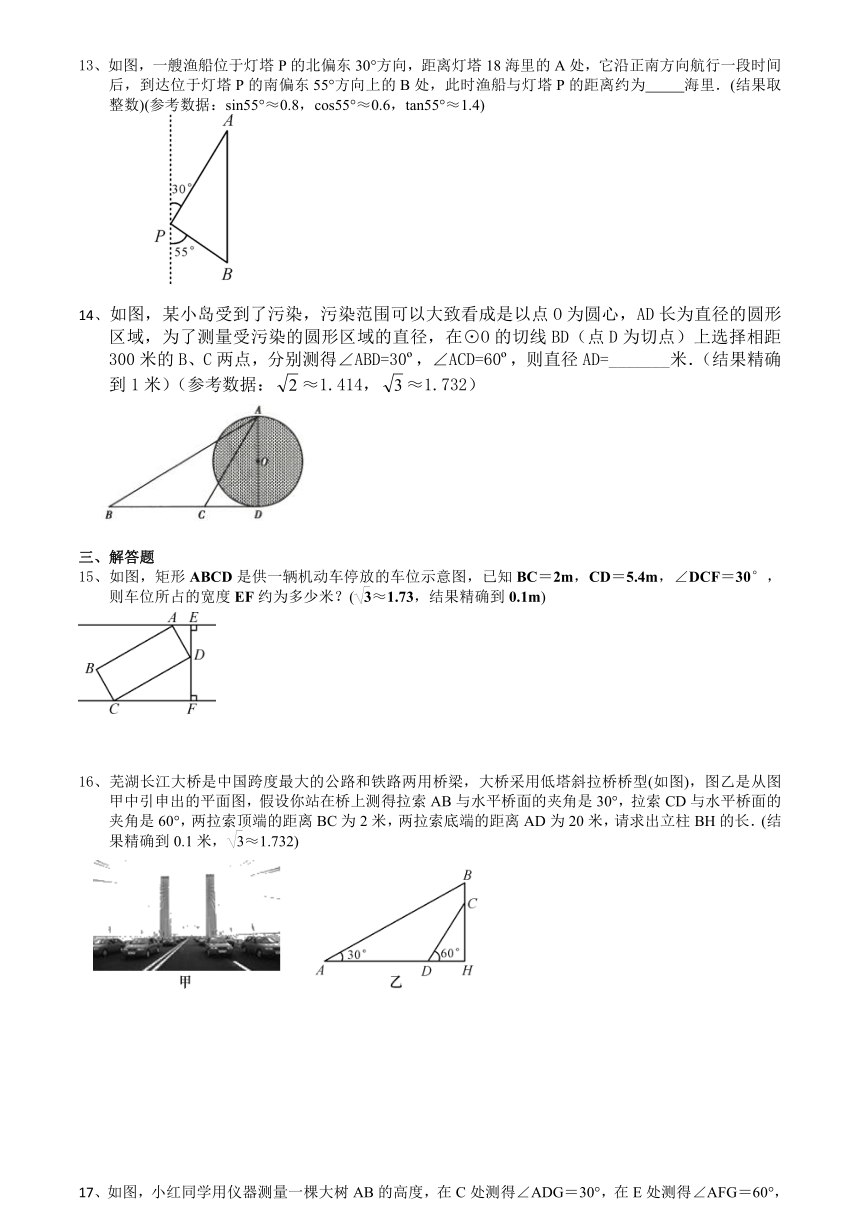
1、如图,一块三角形空地上种草皮绿化,已知AB=20米,AC=30米,∠A=150°,草皮的售价为a元/米2,则购买草皮至少需要( )
A.450a元 B.225a元 C.150a元 D.300a元
2、如图,电线杆AB的中点C处有一标志物,在地面D点处测得标志物的仰角为45°,若点D到电线杆底部点B的距离为a,则电线杆AB的长可表示为( )
A.a B.2a C. D.
3、如图,CD是平面镜,光线从A点出发经CD上点E反射后照射到B点,若入射角为α,AC⊥CD,BD⊥CD,且AC=3,BD=6,CD=11,则tanα值为( )
A. B. C. D.
4、如图,为固定电线杆AC,在离地面高度为6 m的A处引拉线AB,使拉线AB与地面上的BC的夹角为48°,则拉线AB的长度约为( )
(结果精确到0.1 m,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11)
A.6.7 m B.7.2 m C.8.1 m D.9.0 m
5、如图,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在距离北偏东60°方向的500米处,那么水塔所在的位置到公路的距离AB是( )
A.250米 B.250米 C.米 D.500米
6、如图,沿AC方向修山路,为加快施工进度,要在小山另一边同时施工,从AC上的一点B取∠ABD=145°,BD=500米,∠D=55°,使A,C,E在一条直线上,那么开挖点E与D的距离是( )
A.500 sin55° m B.500 cos35° m C.500 cos55° m D.500 tan55° m
7、如图,河流的两岸PQ,MN互相平行,河岸PQ上有一排小树,已知相邻两树CD之间的距离为50 米,某人在河岸MN的A处测得 ,然后沿河岸走了130米到达B处,测得 .则河流的宽度CE为 ( ) 米.
A. 80 B. 40(3-) C. 40(3+) D. 40
8、图是跷跷板的示意图,支柱OC与地面垂直,O是横板AB的中点,AB可以绕着点O上下转动,当A端落地时,∠OAC=20°,横板上下可转动的最大角度(即∠A′OA)是( )
A.80° B.60° C.40° D.20°
二、填空题
9、如图所示,AB是伸缩式的遮阳棚,CD是窗户,要想在夏至的正午时刻阳光刚好不能射入窗户,
则AB的长度是_______米(假设夏至的正午时刻阳光与地平面的夹角为60°).
10、课外活动小组测量学校旗杆的高度.如图,当太阳光线与地面成30°角时,测得旗杆AB在地面上的影长BC为24米,那么旗杆AB的高度约是 米.(结果保留根号)
11、如图是一口直径AB为4米,深BC为2米的圆柱形养蛙池,小青蛙们晚上经常坐在池底中心O观赏月亮,则它们看见月亮的最大视角∠COD=_______度(不考虑青蛙的身高)。
12、如图,河流两岸a、b互相平行,点A、B是河岸a上的两座建筑物,点C、D是河岸b上的两点,A、B的距离约为200米.某人在河岸b上的点P处测得∠APC=75°,∠BPD=30°,则河流的宽度约为 米.
13、如图,一艘渔船位于灯塔P的北偏东30°方向,距离灯塔18海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东55°方向上的B处,此时渔船与灯塔P的距离约为 海里.(结果取整数)(参考数据:sin55°≈0.8,cos55°≈0.6,tan55°≈1.4)
14、如图,某小岛受到了污染,污染范围可以大致看成是以点O为圆心,AD长为直径的圆形区域,为了测量受污染的圆形区域的直径,在⊙O的切线BD(点D为切点)上选择相距300米的B、C两点,分别测得∠ABD=30?,∠ACD=60?,则直径AD=_______米.(结果精确到1米)(参考数据:≈1.414,≈1.732)
三、解答题
15、如图,矩形ABCD是供一辆机动车停放的车位示意图,已知BC=2m,CD=5.4m,∠DCF=30°,则车位所占的宽度EF约为多少米?(≈1.73,结果精确到0.1m)
16、芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,大桥采用低塔斜拉桥桥型(如图),图乙是从图甲中引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端的距离AD为20米,请求出立柱BH的长.(结果精确到0.1米,≈1.732)
17、如图,小红同学用仪器测量一棵大树AB的高度,在C处测得∠ADG=30°,在E处测得∠AFG=60°,CE=8米,仪器高度CD=1.5米,求这棵树AB的高度(结果保留根号).
18、如图,点A、B为地球仪的南、北极点,直线AB与放置地球仪的平面交于点D,所成的角度约为67?,半径OC所在的直线与放置平面垂直,垂足为点E.DE=15 cm,AD=14 cm.求半径OA的长.(精确到0.1 cm)(参考数据:sin 67?≈0.92,cos 67?≈0.39,tan 67?≈2.36)
7.6用锐角三角函数解决问题(2)-苏科版九年级数学下册 巩固训练(答案)
一、选择题
1、如图,一块三角形空地上种草皮绿化,已知AB=20米,AC=30米,∠A=150°,草皮的售价为a元/米2,则购买草皮至少需要( C )
A.450a元 B.225a元 C.150a元 D.300a元
2、如图,电线杆AB的中点C处有一标志物,在地面D点处测得标志物的仰角为45°,若点D到电线杆底部点B的距离为a,则电线杆AB的长可表示为( B )
A.a B.2a C. D.
3、如图,CD是平面镜,光线从A点出发经CD上点E反射后照射到B点,若入射角为α,AC⊥CD,BD⊥CD,且AC=3,BD=6,CD=11,则tanα值为( B )
A. B. C. D.
4、如图,为固定电线杆AC,在离地面高度为6 m的A处引拉线AB,使拉线AB与地面上的BC的夹角为48°,则拉线AB的长度约为(C )
(结果精确到0.1 m,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11)
A.6.7 m B.7.2 m C.8.1 m D.9.0 m
5、如图,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在距离北偏东60°方向的500米处,那么水塔所在的位置到公路的距离AB是(A )
A.250米 B.250米 C.米 D.500米
6、如图,沿AC方向修山路,为加快施工进度,要在小山另一边同时施工,从AC上的一点B取∠ABD=145°,BD=500米,∠D=55°,使A,C,E在一条直线上,那么开挖点E与D的距离是( D )
A.500 sin55° m B.500 cos35° m C.500 cos55° m D.500 tan55° m
7、如图,河流的两岸 , 互相平行,河岸 上有一排小树,已知相邻两树 之间的距离为 米,某人在河岸 的 处测得 ,然后沿河岸走了 米到达 处,测得 .则河流的宽度 为 ( C ) 米.
A. B. C. D.
8、图是跷跷板的示意图,支柱OC与地面垂直,O是横板AB的中点,AB可以绕着点O上下转动,当A端落地时,∠OAC=20°,横板上下可转动的最大角度(即∠A′OA)是(C )
A.80° B.60° C.40° D.20°
二、填空题
9、如图所示,AB是伸缩式的遮阳棚,CD是窗户,要想在夏至的正午时刻阳光刚好不能射入窗户,
则AB的长度是________米(假设夏至的正午时刻阳光与地平面的夹角为60°).
10、课外活动小组测量学校旗杆的高度.如图,当太阳光线与地面成30°角时,测得旗杆AB在地面上的影长BC为24米,那么旗杆AB的高度约是 8 米.(结果保留根号)
11、如图是一口直径AB为4米,深BC为2米的圆柱形养蛙池,小青蛙们晚上经常坐在池底中心O观赏月亮,则它们看见月亮的最大视角∠COD=___90____度(不考虑青蛙的身高)。
12、如图,河流两岸a、b互相平行,点A、B是河岸a上的两座建筑物,点C、D是河岸b上的两点,A、B的距离约为200米.某人在河岸b上的点P处测得∠APC=75°,∠BPD=30°,则河流的宽度约为100 米.
13、如图,一艘渔船位于灯塔P的北偏东30°方向,距离灯塔18海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东55°方向上的B处,此时渔船与灯塔P的距离约为11 海里.(结果取整数)(参考数据:sin55°≈0.8,cos55°≈0.6,tan55°≈1.4)
14、如图,某小岛受到了污染,污染范围可以大致看成是以点O为圆心,AD长为直径的圆形区域,为了测量受污染的圆形区域的直径,在⊙O的切线BD(点D为切点)上选择相距300米的B、C两点,分别测得∠ABD=30?,∠ACD=60?,则直径AD=_______米.(结果精确到1米)(参考数据:≈1.414,≈1.732)
解析 ∠ABD=30?,∠ACD=60?,设CD=x米,则AC=2x米,AD=x米,
∴tan B=,
∴,解得x=150,∴AD=x=×150≈260米.
三、解答题
15、如图,矩形ABCD是供一辆机动车停放的车位示意图,已知BC=2m,CD=5.4m,∠DCF=30°,则车位所占的宽度EF约为多少米?(≈1.73,结果精确到0.1m)
解:∵∠DCF=30°,CD=5.4m,∴在Rt△CDF中,DF=CD=2.7m.
又∵四边形ABCD为矩形,∴AD=BC=2,∠ADC=90°,∴∠ADE+∠CDF=90°.
∵∠DCF+∠CDF=90°,∴∠ADE=∠DCF=30°,
∴在Rt△AED中,DE=AD×cos∠ADE=2×=(m),∴EF=2.7+≈4.4(m).
答:车位所占的宽度EF约为4.4m.
16、芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,大桥采用低塔斜拉桥桥型(如图),图乙是从图甲中引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端的距离AD为20米,请求出立柱BH的长.(结果精确到0.1米,≈1.732)
解:设DH=x米,∵∠CDH=60°,∠H=90°,∴CH=DH·tan60°=x米.
∴BH=BC+CH=(2+x)米.
∵∠A=30°,∴AH=BH=(2+3x)米.
∵AH=AD+DH,∴2+3x=20+x,解得x=10-.
∴BH=2+×(10-)=10-1≈16.3(米). 答:立柱BH的长约为16.3米.
17、如图,小红同学用仪器测量一棵大树AB的高度,在C处测得∠ADG=30°,在E处测得∠AFG=60°,CE=8米,仪器高度CD=1.5米,求这棵树AB的高度(结果保留根号).
解:由题意,得GB=EF=CD=1.5米,DF=CE=8米.
设AG=x米,则GF==x(米).
在Rt△ADG中,tan∠ADG===,
解得x=4.∴AG=4 米. ∴AB=AG+GB=(4+1.5)(米).
18、如图,点A、B为地球仪的南、北极点,直线AB与放置地球仪的平面交于点D,所成的角度约为67?,半径OC所在的直线与放置平面垂直,垂足为点E.DE=15 cm,AD=14 cm.求半径OA的长.(精确到0.1 cm)(参考数据:sin 67?≈0.92,cos 67?≈0.39,tan 67?≈2.36)
解析 在Rt△ODE中,DE=15(cm),∠ODE=67?,
∵cos∠ODE=,∴OD≈≈38.46(cm),
∴OA=OD-AD=38.46-14≈24.5( cm).
答:半径OA的长约为24.5 cm.
一、选择题
1、如图,一块三角形空地上种草皮绿化,已知AB=20米,AC=30米,∠A=150°,草皮的售价为a元/米2,则购买草皮至少需要( )
A.450a元 B.225a元 C.150a元 D.300a元
2、如图,电线杆AB的中点C处有一标志物,在地面D点处测得标志物的仰角为45°,若点D到电线杆底部点B的距离为a,则电线杆AB的长可表示为( )
A.a B.2a C. D.
3、如图,CD是平面镜,光线从A点出发经CD上点E反射后照射到B点,若入射角为α,AC⊥CD,BD⊥CD,且AC=3,BD=6,CD=11,则tanα值为( )
A. B. C. D.
4、如图,为固定电线杆AC,在离地面高度为6 m的A处引拉线AB,使拉线AB与地面上的BC的夹角为48°,则拉线AB的长度约为( )
(结果精确到0.1 m,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11)
A.6.7 m B.7.2 m C.8.1 m D.9.0 m
5、如图,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在距离北偏东60°方向的500米处,那么水塔所在的位置到公路的距离AB是( )
A.250米 B.250米 C.米 D.500米
6、如图,沿AC方向修山路,为加快施工进度,要在小山另一边同时施工,从AC上的一点B取∠ABD=145°,BD=500米,∠D=55°,使A,C,E在一条直线上,那么开挖点E与D的距离是( )
A.500 sin55° m B.500 cos35° m C.500 cos55° m D.500 tan55° m
7、如图,河流的两岸PQ,MN互相平行,河岸PQ上有一排小树,已知相邻两树CD之间的距离为50 米,某人在河岸MN的A处测得 ,然后沿河岸走了130米到达B处,测得 .则河流的宽度CE为 ( ) 米.
A. 80 B. 40(3-) C. 40(3+) D. 40
8、图是跷跷板的示意图,支柱OC与地面垂直,O是横板AB的中点,AB可以绕着点O上下转动,当A端落地时,∠OAC=20°,横板上下可转动的最大角度(即∠A′OA)是( )
A.80° B.60° C.40° D.20°
二、填空题
9、如图所示,AB是伸缩式的遮阳棚,CD是窗户,要想在夏至的正午时刻阳光刚好不能射入窗户,
则AB的长度是_______米(假设夏至的正午时刻阳光与地平面的夹角为60°).
10、课外活动小组测量学校旗杆的高度.如图,当太阳光线与地面成30°角时,测得旗杆AB在地面上的影长BC为24米,那么旗杆AB的高度约是 米.(结果保留根号)
11、如图是一口直径AB为4米,深BC为2米的圆柱形养蛙池,小青蛙们晚上经常坐在池底中心O观赏月亮,则它们看见月亮的最大视角∠COD=_______度(不考虑青蛙的身高)。
12、如图,河流两岸a、b互相平行,点A、B是河岸a上的两座建筑物,点C、D是河岸b上的两点,A、B的距离约为200米.某人在河岸b上的点P处测得∠APC=75°,∠BPD=30°,则河流的宽度约为 米.
13、如图,一艘渔船位于灯塔P的北偏东30°方向,距离灯塔18海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东55°方向上的B处,此时渔船与灯塔P的距离约为 海里.(结果取整数)(参考数据:sin55°≈0.8,cos55°≈0.6,tan55°≈1.4)
14、如图,某小岛受到了污染,污染范围可以大致看成是以点O为圆心,AD长为直径的圆形区域,为了测量受污染的圆形区域的直径,在⊙O的切线BD(点D为切点)上选择相距300米的B、C两点,分别测得∠ABD=30?,∠ACD=60?,则直径AD=_______米.(结果精确到1米)(参考数据:≈1.414,≈1.732)
三、解答题
15、如图,矩形ABCD是供一辆机动车停放的车位示意图,已知BC=2m,CD=5.4m,∠DCF=30°,则车位所占的宽度EF约为多少米?(≈1.73,结果精确到0.1m)
16、芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,大桥采用低塔斜拉桥桥型(如图),图乙是从图甲中引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端的距离AD为20米,请求出立柱BH的长.(结果精确到0.1米,≈1.732)
17、如图,小红同学用仪器测量一棵大树AB的高度,在C处测得∠ADG=30°,在E处测得∠AFG=60°,CE=8米,仪器高度CD=1.5米,求这棵树AB的高度(结果保留根号).
18、如图,点A、B为地球仪的南、北极点,直线AB与放置地球仪的平面交于点D,所成的角度约为67?,半径OC所在的直线与放置平面垂直,垂足为点E.DE=15 cm,AD=14 cm.求半径OA的长.(精确到0.1 cm)(参考数据:sin 67?≈0.92,cos 67?≈0.39,tan 67?≈2.36)
7.6用锐角三角函数解决问题(2)-苏科版九年级数学下册 巩固训练(答案)
一、选择题
1、如图,一块三角形空地上种草皮绿化,已知AB=20米,AC=30米,∠A=150°,草皮的售价为a元/米2,则购买草皮至少需要( C )
A.450a元 B.225a元 C.150a元 D.300a元
2、如图,电线杆AB的中点C处有一标志物,在地面D点处测得标志物的仰角为45°,若点D到电线杆底部点B的距离为a,则电线杆AB的长可表示为( B )
A.a B.2a C. D.
3、如图,CD是平面镜,光线从A点出发经CD上点E反射后照射到B点,若入射角为α,AC⊥CD,BD⊥CD,且AC=3,BD=6,CD=11,则tanα值为( B )
A. B. C. D.
4、如图,为固定电线杆AC,在离地面高度为6 m的A处引拉线AB,使拉线AB与地面上的BC的夹角为48°,则拉线AB的长度约为(C )
(结果精确到0.1 m,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11)
A.6.7 m B.7.2 m C.8.1 m D.9.0 m
5、如图,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在距离北偏东60°方向的500米处,那么水塔所在的位置到公路的距离AB是(A )
A.250米 B.250米 C.米 D.500米
6、如图,沿AC方向修山路,为加快施工进度,要在小山另一边同时施工,从AC上的一点B取∠ABD=145°,BD=500米,∠D=55°,使A,C,E在一条直线上,那么开挖点E与D的距离是( D )
A.500 sin55° m B.500 cos35° m C.500 cos55° m D.500 tan55° m
7、如图,河流的两岸 , 互相平行,河岸 上有一排小树,已知相邻两树 之间的距离为 米,某人在河岸 的 处测得 ,然后沿河岸走了 米到达 处,测得 .则河流的宽度 为 ( C ) 米.
A. B. C. D.
8、图是跷跷板的示意图,支柱OC与地面垂直,O是横板AB的中点,AB可以绕着点O上下转动,当A端落地时,∠OAC=20°,横板上下可转动的最大角度(即∠A′OA)是(C )
A.80° B.60° C.40° D.20°
二、填空题
9、如图所示,AB是伸缩式的遮阳棚,CD是窗户,要想在夏至的正午时刻阳光刚好不能射入窗户,
则AB的长度是________米(假设夏至的正午时刻阳光与地平面的夹角为60°).
10、课外活动小组测量学校旗杆的高度.如图,当太阳光线与地面成30°角时,测得旗杆AB在地面上的影长BC为24米,那么旗杆AB的高度约是 8 米.(结果保留根号)
11、如图是一口直径AB为4米,深BC为2米的圆柱形养蛙池,小青蛙们晚上经常坐在池底中心O观赏月亮,则它们看见月亮的最大视角∠COD=___90____度(不考虑青蛙的身高)。
12、如图,河流两岸a、b互相平行,点A、B是河岸a上的两座建筑物,点C、D是河岸b上的两点,A、B的距离约为200米.某人在河岸b上的点P处测得∠APC=75°,∠BPD=30°,则河流的宽度约为100 米.
13、如图,一艘渔船位于灯塔P的北偏东30°方向,距离灯塔18海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东55°方向上的B处,此时渔船与灯塔P的距离约为11 海里.(结果取整数)(参考数据:sin55°≈0.8,cos55°≈0.6,tan55°≈1.4)
14、如图,某小岛受到了污染,污染范围可以大致看成是以点O为圆心,AD长为直径的圆形区域,为了测量受污染的圆形区域的直径,在⊙O的切线BD(点D为切点)上选择相距300米的B、C两点,分别测得∠ABD=30?,∠ACD=60?,则直径AD=_______米.(结果精确到1米)(参考数据:≈1.414,≈1.732)
解析 ∠ABD=30?,∠ACD=60?,设CD=x米,则AC=2x米,AD=x米,
∴tan B=,
∴,解得x=150,∴AD=x=×150≈260米.
三、解答题
15、如图,矩形ABCD是供一辆机动车停放的车位示意图,已知BC=2m,CD=5.4m,∠DCF=30°,则车位所占的宽度EF约为多少米?(≈1.73,结果精确到0.1m)
解:∵∠DCF=30°,CD=5.4m,∴在Rt△CDF中,DF=CD=2.7m.
又∵四边形ABCD为矩形,∴AD=BC=2,∠ADC=90°,∴∠ADE+∠CDF=90°.
∵∠DCF+∠CDF=90°,∴∠ADE=∠DCF=30°,
∴在Rt△AED中,DE=AD×cos∠ADE=2×=(m),∴EF=2.7+≈4.4(m).
答:车位所占的宽度EF约为4.4m.
16、芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,大桥采用低塔斜拉桥桥型(如图),图乙是从图甲中引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端的距离AD为20米,请求出立柱BH的长.(结果精确到0.1米,≈1.732)
解:设DH=x米,∵∠CDH=60°,∠H=90°,∴CH=DH·tan60°=x米.
∴BH=BC+CH=(2+x)米.
∵∠A=30°,∴AH=BH=(2+3x)米.
∵AH=AD+DH,∴2+3x=20+x,解得x=10-.
∴BH=2+×(10-)=10-1≈16.3(米). 答:立柱BH的长约为16.3米.
17、如图,小红同学用仪器测量一棵大树AB的高度,在C处测得∠ADG=30°,在E处测得∠AFG=60°,CE=8米,仪器高度CD=1.5米,求这棵树AB的高度(结果保留根号).
解:由题意,得GB=EF=CD=1.5米,DF=CE=8米.
设AG=x米,则GF==x(米).
在Rt△ADG中,tan∠ADG===,
解得x=4.∴AG=4 米. ∴AB=AG+GB=(4+1.5)(米).
18、如图,点A、B为地球仪的南、北极点,直线AB与放置地球仪的平面交于点D,所成的角度约为67?,半径OC所在的直线与放置平面垂直,垂足为点E.DE=15 cm,AD=14 cm.求半径OA的长.(精确到0.1 cm)(参考数据:sin 67?≈0.92,cos 67?≈0.39,tan 67?≈2.36)
解析 在Rt△ODE中,DE=15(cm),∠ODE=67?,
∵cos∠ODE=,∴OD≈≈38.46(cm),
∴OA=OD-AD=38.46-14≈24.5( cm).
答:半径OA的长约为24.5 cm.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
