沪教版(上海)初中数学九年级第一学期 25.4 (3)解直角三角形的应用 课件(共15张ppt)
文档属性
| 名称 | 沪教版(上海)初中数学九年级第一学期 25.4 (3)解直角三角形的应用 课件(共15张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 21:17:05 | ||
图片预览






文档简介
25.4(3)解直角三角形的应用
我们在生活中会见到很多斜坡,有的斜坡比较陡,有的比较平缓。
这只是我们的直观认识,我们怎么来定量的表示坡的陡缓程度呢?
α
β
γ
如图三个斜坡,其坡面与水平面的夹角分别为 、 、 ,且
观察三个斜坡的情况。你觉得斜坡的陡缓与什么有关?有怎样的关系?
发现一:坡角越大,斜坡越陡。
坡角:坡面与水平面的夹角
铅垂高度h
水平宽度l
固定AB的长度不变
的前提下,
改变坡角α的大小,
请观察铅垂高度和水平宽度的变化,
有什么发现吗?
发现二:铅垂高度与水平宽度的比值越大,斜坡越陡。
α
l
h
i= h : l
1、坡角
坡面与水平面的夹角叫做坡角,记作α 。
2、坡度(或坡比)
坡度通常写成1∶m的形式,如i= =1∶1.5
如图所示,坡面的铅垂高度h和水平宽度l
的比叫做坡面的坡度(或坡比),记作i, 即
3、坡度与坡角的关系
坡度等于坡角的正切值
坡面
水平面
巩固练习
A
B
C
通过这个练习,你有什么感想?
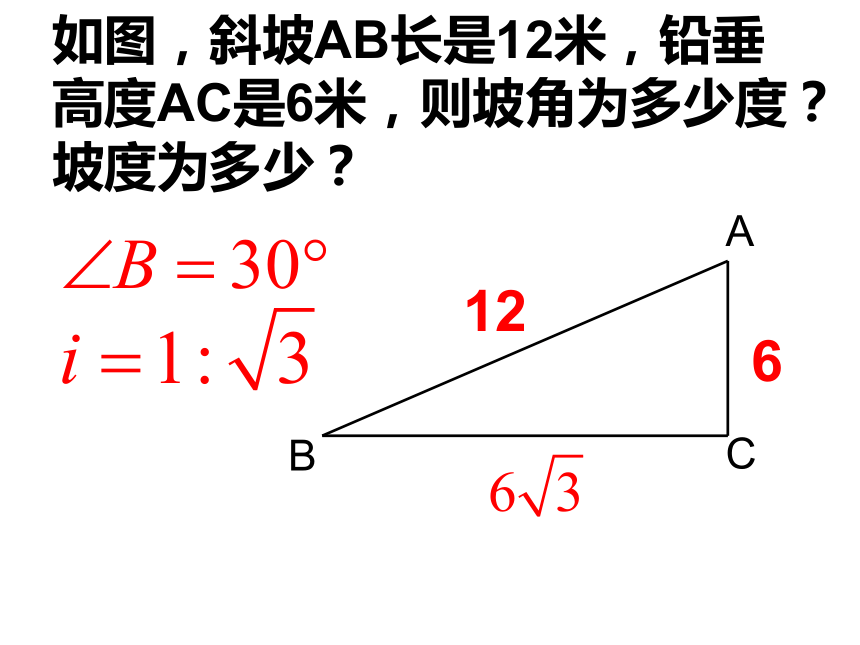
如图,斜坡AB长是12米,铅垂高度AC是6米,则坡角为多少度?坡度为多少?
A
B
C
12
6
例题1:一座大楼前的残疾人通道是斜坡,沿着通道走2.21米可进入楼厅,楼厅比楼外的地面高0.21米。
(1)根据题意,画出示意图形,并标注相关数据;
(2)求残疾人通道的坡度。
解 过点A作水平线l,再作BC⊥l,垂足为点C.
根据题意,可知
AB=2.21米,BC=0.21米.
在Rt△ABC中,
答:残疾人通道的坡度约为1:10.48。
若AB=S,BC=h,求坡度。
解题小结
关键:构造直角三角形
思路:实际问题
直角三角形问题
转化
例题2:如图,一段铁路路基的横断面为等腰梯形ABCD,路基顶宽BC为2.8米,路基高为1.2米,斜坡AB的坡度为i=1:1.6 .
(1)计算路基的下底宽(精确到0.1米).
(2)求坡角 (精确到1°).
解 分别过点B、C作BE⊥AD、 CF⊥AD,垂足分别为
点E、F.
根据题意,可知
BE=1.2(米),AE=DF,EF=BC=2.8(米).
在Rt△ABE中,
答:路基的下底宽约为6.6米,坡角约为
课堂总结:
1、坡度与坡角的概念;
2、等腰梯形中常见辅助线:添高;
3、运用转化的数学思想方法将实际问题化归为解直角三角形的问题。
扩展问题:
有一段防洪大堤,其横断面为梯形 , 。斜坡AD的坡度 ,斜坡BC的坡度 ,大堤顶宽DC为6米, 为了增强抗洪能力,现将大堤加高,加高部分的横断面为梯形DCFE, ,点E、F分别在AD、BC的延长线上(如图)。当新大堤顶宽EF为4.8米时,大堤加高了几米?
收获经验
2、解直角三角形的问题往往与其他知识联系,因此,我们要善于要把解直角三角形作为一种工具,能在解决各种数学问题时合理运用。
1、学以致用
我们学习数学的目的就是解决实际生活中存在的数学问题,因此,在解题时首先要读懂题意,把实际问题转化为数学问题。
对于生活中存在的解直角三角形的问题,关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构造直角三角形(作某边上的高是常用的辅助线)。
我们在生活中会见到很多斜坡,有的斜坡比较陡,有的比较平缓。
这只是我们的直观认识,我们怎么来定量的表示坡的陡缓程度呢?
α
β
γ
如图三个斜坡,其坡面与水平面的夹角分别为 、 、 ,且
观察三个斜坡的情况。你觉得斜坡的陡缓与什么有关?有怎样的关系?
发现一:坡角越大,斜坡越陡。
坡角:坡面与水平面的夹角
铅垂高度h
水平宽度l
固定AB的长度不变
的前提下,
改变坡角α的大小,
请观察铅垂高度和水平宽度的变化,
有什么发现吗?
发现二:铅垂高度与水平宽度的比值越大,斜坡越陡。
α
l
h
i= h : l
1、坡角
坡面与水平面的夹角叫做坡角,记作α 。
2、坡度(或坡比)
坡度通常写成1∶m的形式,如i= =1∶1.5
如图所示,坡面的铅垂高度h和水平宽度l
的比叫做坡面的坡度(或坡比),记作i, 即
3、坡度与坡角的关系
坡度等于坡角的正切值
坡面
水平面
巩固练习
A
B
C
通过这个练习,你有什么感想?
如图,斜坡AB长是12米,铅垂高度AC是6米,则坡角为多少度?坡度为多少?
A
B
C
12
6
例题1:一座大楼前的残疾人通道是斜坡,沿着通道走2.21米可进入楼厅,楼厅比楼外的地面高0.21米。
(1)根据题意,画出示意图形,并标注相关数据;
(2)求残疾人通道的坡度。
解 过点A作水平线l,再作BC⊥l,垂足为点C.
根据题意,可知
AB=2.21米,BC=0.21米.
在Rt△ABC中,
答:残疾人通道的坡度约为1:10.48。
若AB=S,BC=h,求坡度。
解题小结
关键:构造直角三角形
思路:实际问题
直角三角形问题
转化
例题2:如图,一段铁路路基的横断面为等腰梯形ABCD,路基顶宽BC为2.8米,路基高为1.2米,斜坡AB的坡度为i=1:1.6 .
(1)计算路基的下底宽(精确到0.1米).
(2)求坡角 (精确到1°).
解 分别过点B、C作BE⊥AD、 CF⊥AD,垂足分别为
点E、F.
根据题意,可知
BE=1.2(米),AE=DF,EF=BC=2.8(米).
在Rt△ABE中,
答:路基的下底宽约为6.6米,坡角约为
课堂总结:
1、坡度与坡角的概念;
2、等腰梯形中常见辅助线:添高;
3、运用转化的数学思想方法将实际问题化归为解直角三角形的问题。
扩展问题:
有一段防洪大堤,其横断面为梯形 , 。斜坡AD的坡度 ,斜坡BC的坡度 ,大堤顶宽DC为6米, 为了增强抗洪能力,现将大堤加高,加高部分的横断面为梯形DCFE, ,点E、F分别在AD、BC的延长线上(如图)。当新大堤顶宽EF为4.8米时,大堤加高了几米?
收获经验
2、解直角三角形的问题往往与其他知识联系,因此,我们要善于要把解直角三角形作为一种工具,能在解决各种数学问题时合理运用。
1、学以致用
我们学习数学的目的就是解决实际生活中存在的数学问题,因此,在解题时首先要读懂题意,把实际问题转化为数学问题。
对于生活中存在的解直角三角形的问题,关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构造直角三角形(作某边上的高是常用的辅助线)。
