冀教版九年级下册30.4二次函数的应用课件(共21张ppt)
文档属性
| 名称 | 冀教版九年级下册30.4二次函数的应用课件(共21张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 281.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-28 00:00:00 | ||
图片预览







文档简介
二次函数的应用
二次函数的图象与x轴有没有交点,由什么决定?
复习思考
由b?-4ac的符号决定
b?-4ac﹥0,有两个交点
b?-4ac=0,只有一个交点
b?-4ac﹤0,没有交点
求出二次函数y=10x-5x?图象的顶点坐标,与x轴的交点坐标,并画出函数的大致图象
探究:计算机把数据存储在磁盘上,磁盘是带有磁性物质的圆盘,磁盘上有一些同心圆轨道,叫做磁道,如图,现有一张半径为45mm的磁盘.
(3)如果各磁道的存储单元数目与最内磁道相同.最内磁道的半径r是多少时,磁盘的存储量最大?
(1)磁盘最内磁道的半径为r mm,其上每0.015mm的弧长为1个存储单元,这条磁道有多少个存储单元?
(2)磁盘上各磁道之间的宽度必须不小于0.3mm,磁盘的外圆周不是磁道,这张磁盘最多有多少条磁道?
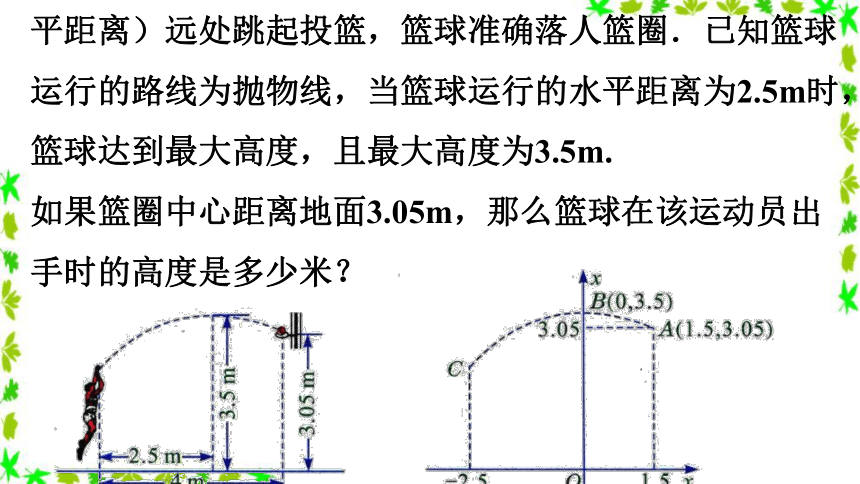
例1 如图30-4-1,一名运动员在距离篮圈中心4m(水平距离)远处跳起投篮,篮球准确落人篮圈.已知篮球运行的路线为抛物线,当篮球运行的水平距离为2.5m时,篮球达到最大高度,且最大高度为3.5m.
如果篮圈中心距离地面3.05m,那么篮球在该运动员出手时的高度是多少米?
解:如图30-4-2,建立直角坐标系,篮圈中心为点A(1.5,3.05),篮球在最大高度时的位置为点B(0,3.5).以点C表示运动员投篮球的出手处.
设以y轴(直线x=0)为对称轴的抛物线为y=a(x-0)2+k,即y=ax2+k,而点A,B在这条抛物线上,所以有
解得
y
0
x
5
10
15
20
25
30
1
2
3
4
5
7
8
9
1o
-1
6
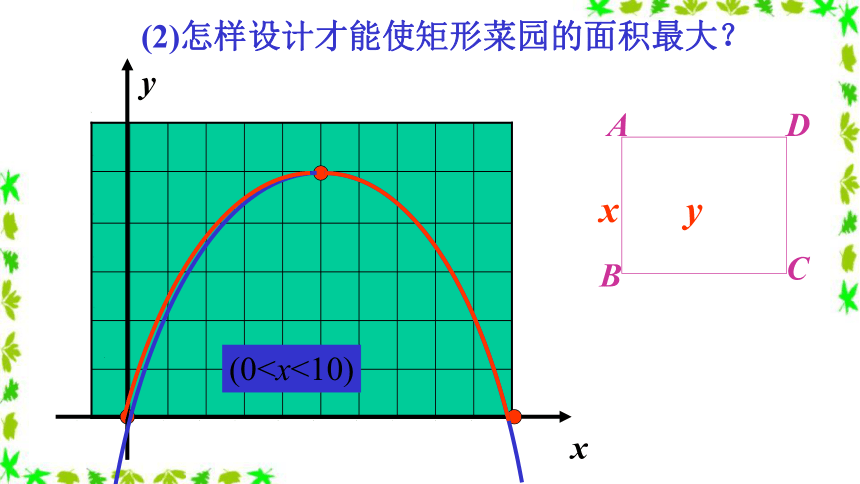
(1) 请用长20米的篱笆设计一个矩形的菜园.
(2)怎样设计才能使矩形菜园的面积最大?
A
B
C
D
x
y
(0(1)求y与x的函数关系式及
自变量的取值范围;
(2)怎样围才能使菜园的面积最大?
最大面积是多少?
如图,用长20米的篱笆围成一个一面靠
墙的长方形的菜园,设菜园的宽为x米,面
积为y平方米.
A
B
C
D
如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米.
(1)求S与x的函数关系式及自变量的取值范围;
(2)当x取何值时所围成的花圃面积最大,最大值是多少?
(3)若墙的最大可用长度为8米,则求围成花圃的最大面积.
A
B
C
D
A
B
C
D
解:
(1) ∵ AB为x米、篱笆长为24米
∴ 花圃宽为(24-4x)米
(3) ∵墙的可用长度为8米
(2)当x= 时,S最大值= =36(平方米)
∴ S=x(24-4x)
=-4x2+24 x (0∴ 0<24-4x ≤6 4≤x<6
∴当x=4cm时,S最大值=32 平方米
例2 用总长度为24m的不锈钢材料制成如图30-4-6所示的外观为矩形的框架,其横档和竖档分别与AD,AB平行.设AB=xm,当x为多少时,矩形框架
ABCD的面积S最大?最大面积是多少平方米?
解:∵
∴当x=3时,S有最大值,且S最大=12m2.
答:当x=3时,矩形框架ABCD的面积最大,最大面积为12m2.
(1).设矩形的一边AB=xm,那么AD边的长度如何表示?
(2).设矩形的面积为ym2,当x取何值时,y的最大值是多少?
何时面积最大
如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.
M
N
40m
30m
A
B
C
D
┐
(1).设矩形的一边BC=xm,那么AB边的长度如何表示?
(2).设矩形的面积为ym2,当x取何值时,y的最大值是多少?
何时面积最大
如图,在一个直角三角形的内部作一个矩形ABCD,其顶点A和点D分别在两直角边上,BC在斜边上.
A
B
C
D
┐
M
N
P
40m
30m
xm
bm
H
G
┛
┛
例3 一工艺师生产的某种产品按质量分为9个档次.第1档次(最低档次)的产品一天能生产80件,每件可获利润12元.产品每提高一个档次,每件产品的利润增加2元,但一天产量减少4件.如果只从生产利润这一角度考虑,他生产哪个档次的产品,可获得最大利润?
解:设生产x档次的产品时,每天所获得的利润为w元,
w=[12+2(x-1)] [80-4(x-1)]
=(10+2x)(84-4x)
=-8x2+128x+840
=-8(x-8)2+1352.
当x=8时,w有最大值,且w最大=1352.
答:该工艺师生产第8档次的产品,可使每天获得的利润最大,最大利润为1352元.
则
何时窗户通过的光线最多
用长为6m的铝合金型材做一个形状如图26.2.5所示的矩形窗框.窗框的高与宽各为多少时,它的透光面积最大?最大透光面积是多少?(铝合金型材宽度不计)
解 设矩形窗框的宽为xm,则高为
这里应有x>0,且 >0.故0矩形窗框的透光面积y与x之间的函数
关系式是
即
配方得
所以当x=1时,函数取得最大值,最大值y=1.5.
x=1满足0因此,所做矩形窗框的宽为1m、高为1.5m时,它的透光面积最大,最大面积是1.5m2.
例4 如图30-4-7,已知边长为1的正方形ABCD,在BC边上有一动点E,连接AE,作EF⊥AE,交CD边于点F.
(1)CF的长可能等于 吗?
(2)点E在什么位置时,CF的长为 ?
解:设BE=x,CF=y.
∵∠BAE=∠CEF,
∴Rt△ABE∽Rt△ECF.
∴ 即
∴
(1)∵y最大= ,
∴CF的长不可能等于 .
(2)设 即
解得
∴当BE的长为 或 时,均有CF的长为 .
1.某工厂为了存放材料,需要围一个周长160米的矩形场地,问矩形的长和宽各取多少米,才能使存放场地的面积最大.
2.窗的形状是矩形上面加一个半圆.窗的周长等于6cm,要使窗能透过最多的光线,它的尺寸应该如何设计?
B
C
D
A
O
练一练:
2.用一块宽为1.2m的长方形铁板弯起两边做一个水槽,水槽的横断面为底角120?的等腰梯形.要使水槽的横断面积最大,它的侧面AB应该是多长?
A
D
120?
B
C
1.理解问题;
“二次函数应用” 的思路
你能总结一下解决此类问题的基本思路吗?与同伴交流.
2.分析问题中的变量和常量,以及它们之间的关系;
3.用数学的方式表示出它们之间的关系;
4.做数学求解;
5.检验结果的合理性,拓展等.
二次函数的图象与x轴有没有交点,由什么决定?
复习思考
由b?-4ac的符号决定
b?-4ac﹥0,有两个交点
b?-4ac=0,只有一个交点
b?-4ac﹤0,没有交点
求出二次函数y=10x-5x?图象的顶点坐标,与x轴的交点坐标,并画出函数的大致图象
探究:计算机把数据存储在磁盘上,磁盘是带有磁性物质的圆盘,磁盘上有一些同心圆轨道,叫做磁道,如图,现有一张半径为45mm的磁盘.
(3)如果各磁道的存储单元数目与最内磁道相同.最内磁道的半径r是多少时,磁盘的存储量最大?
(1)磁盘最内磁道的半径为r mm,其上每0.015mm的弧长为1个存储单元,这条磁道有多少个存储单元?
(2)磁盘上各磁道之间的宽度必须不小于0.3mm,磁盘的外圆周不是磁道,这张磁盘最多有多少条磁道?
例1 如图30-4-1,一名运动员在距离篮圈中心4m(水平距离)远处跳起投篮,篮球准确落人篮圈.已知篮球运行的路线为抛物线,当篮球运行的水平距离为2.5m时,篮球达到最大高度,且最大高度为3.5m.
如果篮圈中心距离地面3.05m,那么篮球在该运动员出手时的高度是多少米?
解:如图30-4-2,建立直角坐标系,篮圈中心为点A(1.5,3.05),篮球在最大高度时的位置为点B(0,3.5).以点C表示运动员投篮球的出手处.
设以y轴(直线x=0)为对称轴的抛物线为y=a(x-0)2+k,即y=ax2+k,而点A,B在这条抛物线上,所以有
解得
y
0
x
5
10
15
20
25
30
1
2
3
4
5
7
8
9
1o
-1
6
(1) 请用长20米的篱笆设计一个矩形的菜园.
(2)怎样设计才能使矩形菜园的面积最大?
A
B
C
D
x
y
(0
自变量的取值范围;
(2)怎样围才能使菜园的面积最大?
最大面积是多少?
如图,用长20米的篱笆围成一个一面靠
墙的长方形的菜园,设菜园的宽为x米,面
积为y平方米.
A
B
C
D
如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米.
(1)求S与x的函数关系式及自变量的取值范围;
(2)当x取何值时所围成的花圃面积最大,最大值是多少?
(3)若墙的最大可用长度为8米,则求围成花圃的最大面积.
A
B
C
D
A
B
C
D
解:
(1) ∵ AB为x米、篱笆长为24米
∴ 花圃宽为(24-4x)米
(3) ∵墙的可用长度为8米
(2)当x= 时,S最大值= =36(平方米)
∴ S=x(24-4x)
=-4x2+24 x (0
∴当x=4cm时,S最大值=32 平方米
例2 用总长度为24m的不锈钢材料制成如图30-4-6所示的外观为矩形的框架,其横档和竖档分别与AD,AB平行.设AB=xm,当x为多少时,矩形框架
ABCD的面积S最大?最大面积是多少平方米?
解:∵
∴当x=3时,S有最大值,且S最大=12m2.
答:当x=3时,矩形框架ABCD的面积最大,最大面积为12m2.
(1).设矩形的一边AB=xm,那么AD边的长度如何表示?
(2).设矩形的面积为ym2,当x取何值时,y的最大值是多少?
何时面积最大
如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.
M
N
40m
30m
A
B
C
D
┐
(1).设矩形的一边BC=xm,那么AB边的长度如何表示?
(2).设矩形的面积为ym2,当x取何值时,y的最大值是多少?
何时面积最大
如图,在一个直角三角形的内部作一个矩形ABCD,其顶点A和点D分别在两直角边上,BC在斜边上.
A
B
C
D
┐
M
N
P
40m
30m
xm
bm
H
G
┛
┛
例3 一工艺师生产的某种产品按质量分为9个档次.第1档次(最低档次)的产品一天能生产80件,每件可获利润12元.产品每提高一个档次,每件产品的利润增加2元,但一天产量减少4件.如果只从生产利润这一角度考虑,他生产哪个档次的产品,可获得最大利润?
解:设生产x档次的产品时,每天所获得的利润为w元,
w=[12+2(x-1)] [80-4(x-1)]
=(10+2x)(84-4x)
=-8x2+128x+840
=-8(x-8)2+1352.
当x=8时,w有最大值,且w最大=1352.
答:该工艺师生产第8档次的产品,可使每天获得的利润最大,最大利润为1352元.
则
何时窗户通过的光线最多
用长为6m的铝合金型材做一个形状如图26.2.5所示的矩形窗框.窗框的高与宽各为多少时,它的透光面积最大?最大透光面积是多少?(铝合金型材宽度不计)
解 设矩形窗框的宽为xm,则高为
这里应有x>0,且 >0.故0
关系式是
即
配方得
所以当x=1时,函数取得最大值,最大值y=1.5.
x=1满足0
例4 如图30-4-7,已知边长为1的正方形ABCD,在BC边上有一动点E,连接AE,作EF⊥AE,交CD边于点F.
(1)CF的长可能等于 吗?
(2)点E在什么位置时,CF的长为 ?
解:设BE=x,CF=y.
∵∠BAE=∠CEF,
∴Rt△ABE∽Rt△ECF.
∴ 即
∴
(1)∵y最大= ,
∴CF的长不可能等于 .
(2)设 即
解得
∴当BE的长为 或 时,均有CF的长为 .
1.某工厂为了存放材料,需要围一个周长160米的矩形场地,问矩形的长和宽各取多少米,才能使存放场地的面积最大.
2.窗的形状是矩形上面加一个半圆.窗的周长等于6cm,要使窗能透过最多的光线,它的尺寸应该如何设计?
B
C
D
A
O
练一练:
2.用一块宽为1.2m的长方形铁板弯起两边做一个水槽,水槽的横断面为底角120?的等腰梯形.要使水槽的横断面积最大,它的侧面AB应该是多长?
A
D
120?
B
C
1.理解问题;
“二次函数应用” 的思路
你能总结一下解决此类问题的基本思路吗?与同伴交流.
2.分析问题中的变量和常量,以及它们之间的关系;
3.用数学的方式表示出它们之间的关系;
4.做数学求解;
5.检验结果的合理性,拓展等.
